Krümmungsverhalten
Online Rechner
Der Online Rechner von Simplexy kann dir beim Krümmungsverhalten einer Funktion sehr helfen. Mit dem Rechner kannst du dir den Graphen einer Funktion zeichnen lassen, die Funktion ableiten und viel mehr.
Krümmungsverhalten einer Funktion
Um das Krümmungsverhalten einer Funktion zu bestimmen verwendet man die zweite Ableitung \(f''(x)\), dabei gilt:
- \(f''(x)\gt 0 \,\,\,\implies\,\,\,f(x)\) ist links gekrümmt
- \(f''(x)\lt 0 \,\,\,\implies\,\,\,f(x)\) ist rechts gekrümmt
Beim Thema Wendepunkt einer Funktion, haben wir uns bereits mit der Krümmung von Funktionen beschäftigt. Dort haben wir festgestellt, dass eine Funktion seine Krümmung an einem Wendepunkt ändert. Das gleiche passiert auch bei einem Sattelpunkt.
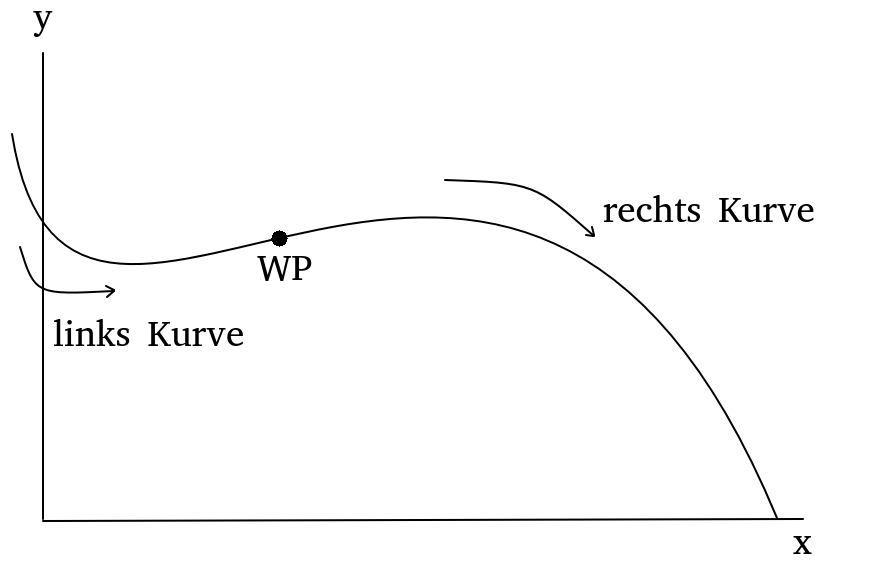
An einem Sattelpunkt und an einem Wendepunkt ändert sich die Krümmung einer Funktion.
Eine Funkion kann ohne die Existenz eines Sattelpunkts oder eines Wendepunkts eine Krümmung besitzen. Um herauszufinden ob eine Funktion eine Krümmung besitzt, muss man sich mit der zwieten Ableitung \(f''(x)\) beschäftigen.
Funktion ohne Krümmung
Betrachten wir zunächst die Funkiton
\(f(x)=x\)
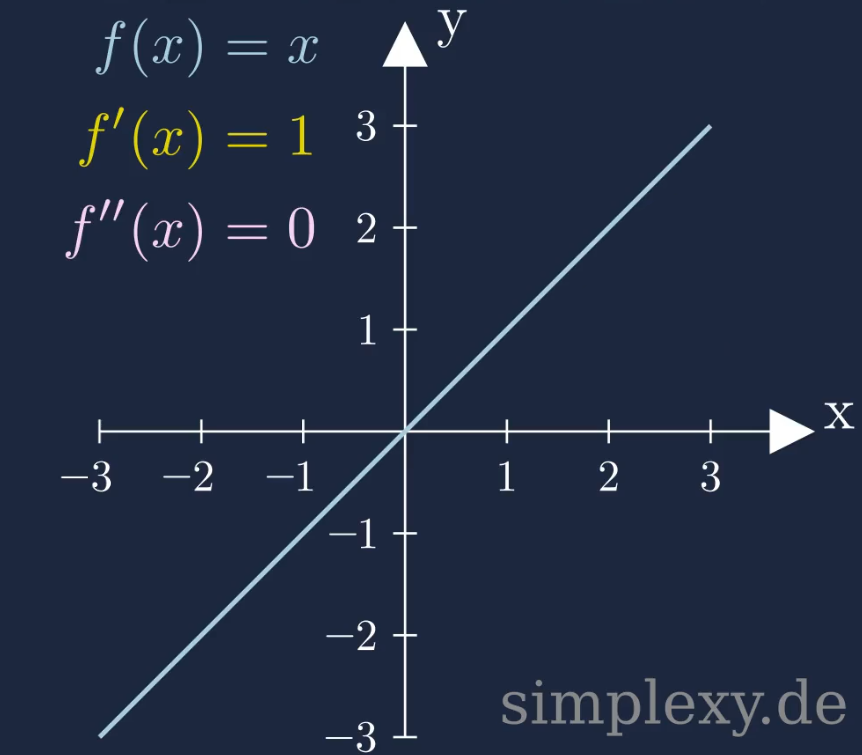
Es handelt sich hierbei um eine Lineare-Funktion. Wir können die zweite Ableitung der Funktion berechnen:
\(\begin{aligned} f(x)&=x\\ \\ f'(x)&=1\\ \\ f''(x)&=0 \end{aligned}\)
Die zweite Ableitung einer Funktion gibt uns an ob eine Funktion gekrümmt ist. In dem Fall ist die zweite Ableitung gleich Null. Daraus können wir schließen, dass die Lineare-Funktion keine Krümmung besitzt.
Krümmung einer Parabel
In diesem Abschnitt möchten wir das Krümmungsverhalten einer Parabel untersuchen. Wir werden feststellen, das Parabeln sowohl eine Linkskrümmung als auch eine Rechtskrümmung besitzten können.
Linkskrümmung
Wir untersuchen zunächst die Normalparabel:
\(f(x)=x^2\)
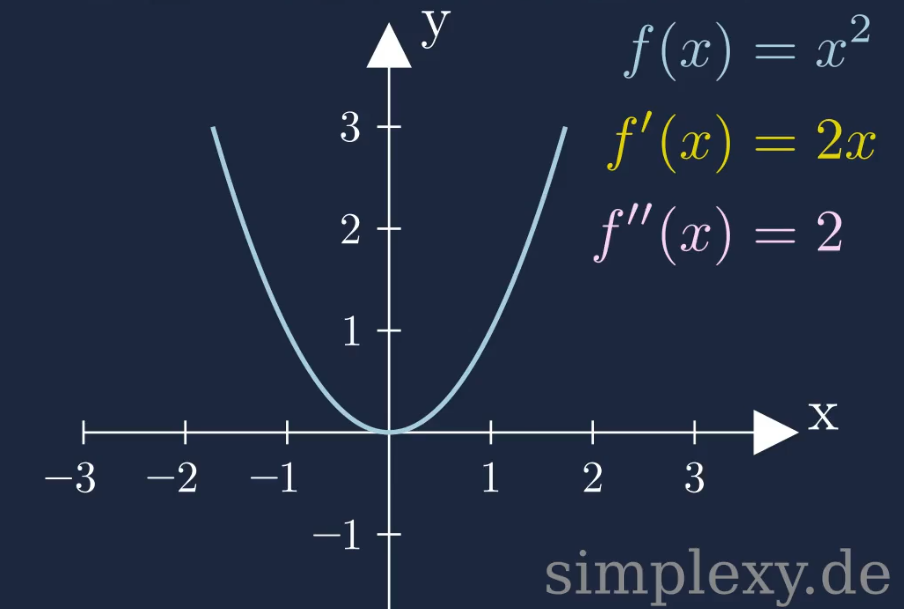
Um Aussagen über das Krümmungsverhalten zu Treffen, müssen wir die zweite Ableitung berechnen:
\(\begin{aligned} f(x)&=x^2\\ \\ f'(x)&=2x\\ \\ f''(x)&=2 \end{aligned}\)
In diesen Fall ist die zweite Ableitung ungleich Null, damit besitzt diese Funktion eine Krümmung. Zudem ist die zweite Ableitung größer als Null, wir haben es also mit einer Linkskrümmung zu tun.
Linkskrümmung
\(f''(x)\gt 0 \,\,\,\implies\,\,\,f(x)\) ist links gekrümmt
Rechtskrümmung
Wir betrachten nun die Negative-Parabel:
\(f(x)=-x^2\)
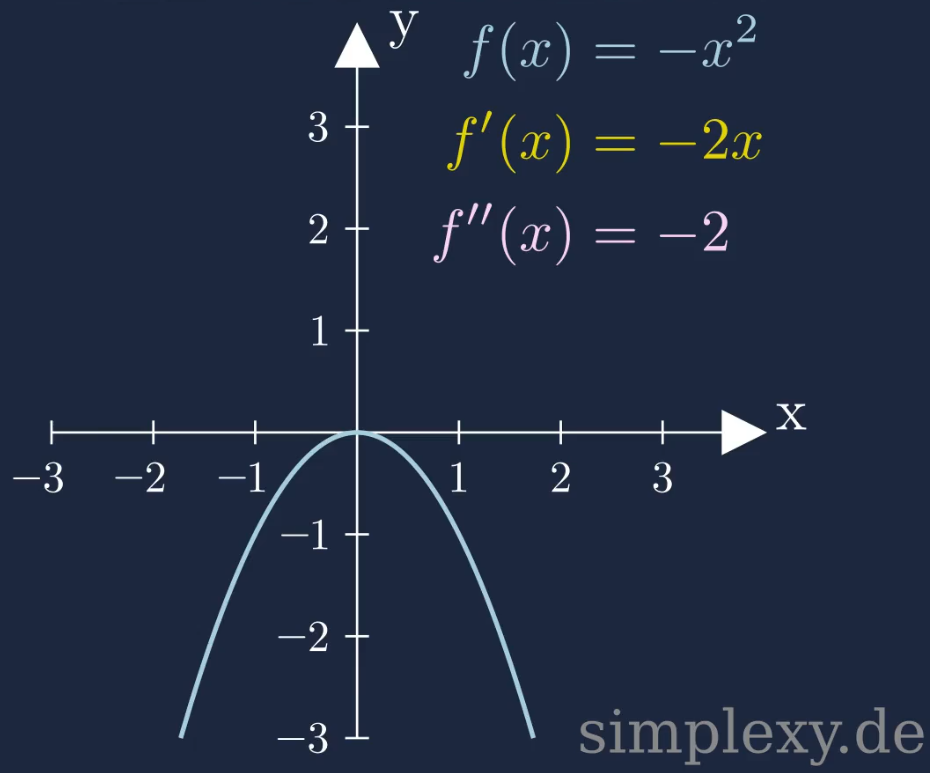
Wir benötigen wieder die zweite Ableitung um die Krümmung zu untersuchen:
\(\begin{aligned} f(x)&=-x^2\\ \\ f'(x)&=-2x\\ \\ f''(x)&=-2 \end{aligned}\)
In diesem Fall ist die zweite Ableitung kleiner als Null (negativ). Wir haben es also mit einer Rechtskrümmung zu tun.
Rechtskrümmung
\(f''(x)\lt 0 \,\,\,\implies\,\,\,f(x)\) ist rechts gekrümmt
Merkhilfe
- Ist die 2.Ableitung negativ, so ist die Funktion rechtsgekrümmt.
- Ist die 2.Ableitung positiv, so ist die Funktion linksgekrümmt.
Änderung der Krümmung
Wie bereits erwähnt findet an einem Sattelpunkt und an einem Wendepunkt eine Änderung der Krümmung statt. Wir wollen dies nun am Beispiel der folgenden Funktion untersuchen:
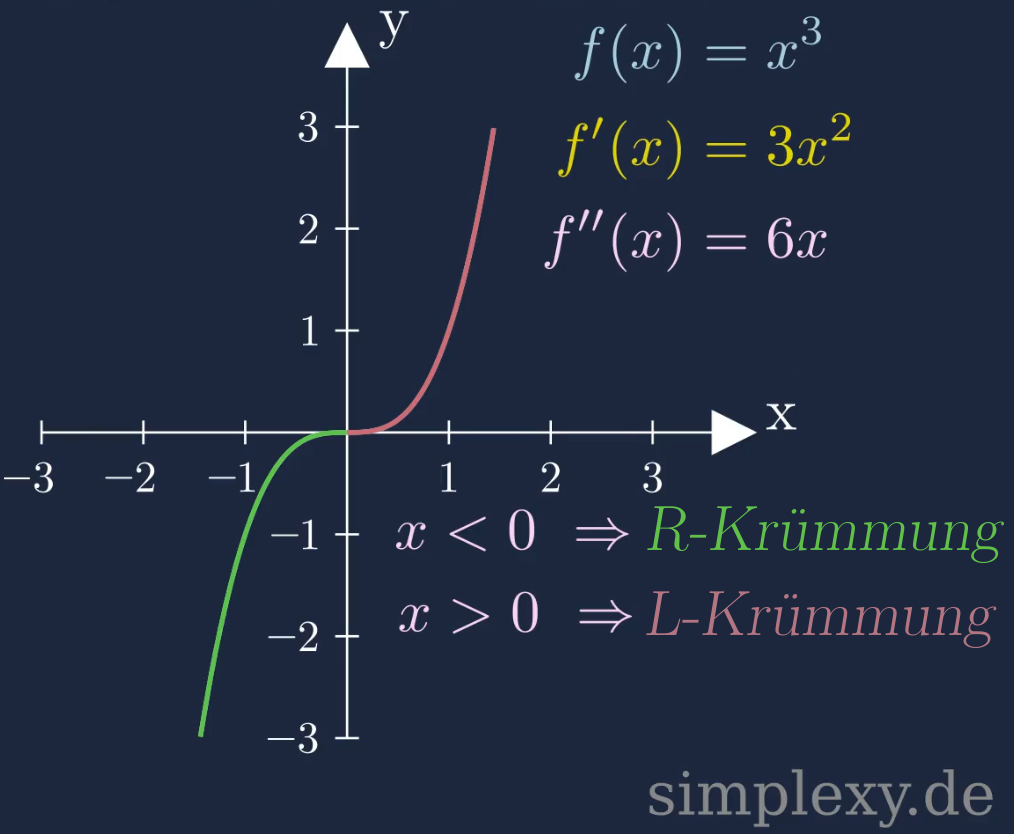
\(f(x)=x^3\)
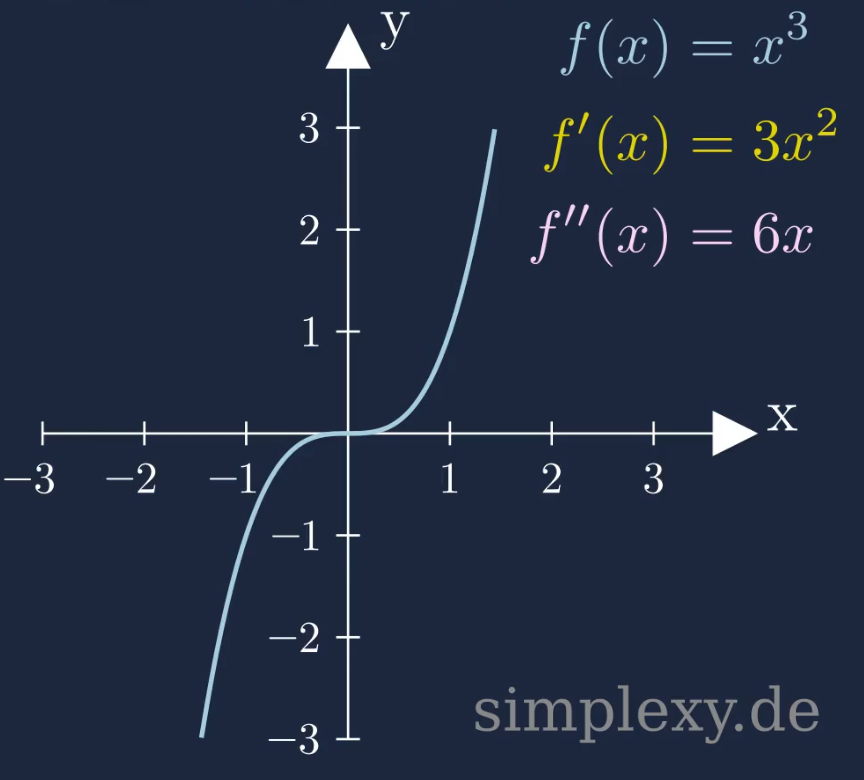
Wir sehen das die Funktion einen Sattelpunkt besitzt. Um das Krümmungsverhalten zu untersuchen, müssen wir als erstes den Sattelpunkt berechnen. Dazu müssen wir die zweite Ableitung der Funktion null setzen. Wir rechnen zunächste die zweite Ableitung aus:
\(\begin{aligned} f(x)&=x^3\\ \\ f'(x)&=3x^2\\ \\ f''(x)&=6x \end{aligned}\)
Um den Sattelpunkt zu berechnen, müssen wir die zweite Ableitung null setzen und nach \(x\) umstellen:
\(\begin{aligned} &f''(x)=6x=0\\ &\implies x=0 \end{aligned}\)
Der Sattelpunkt befindet sich am Wert \(x=0\). An diesem \(x\)-Wert ändert sich die Krümmung der Funktion. Um rauszufinden, welche Krümmung im Intervall \((-\infty,0)\) vorliegt, müssen wir einen \(x\)-Wert aus diesem Intervall in die zweite Ableitung einsetzen. Wir mach dies für den \(x\)-Wert \(x=-1\):
\(\begin{aligned} f''(-1)&=6\cdot (-1)\\ &=-6 \end{aligned}\)
Die zweite Ableitung am \(x\)-Wert \(x=-1\) ist negativ. Damit liegt dort eine Rechtskrümmung vor.
Nun müssen wir noch die Krümmung im Intervall \((0,\infty)\) bestimmen. Dazu setzen wir einen \(x\)-Wert aus diesem Intervall in die zweite Ableitung ein. Wir machen dies für den \(x\)-Wert \(x=1\):
\(\begin{aligned} f''(1)&=6\cdot 1\\ &=6 \end{aligned}\)
Wir erhalten nun einen positiven Wert. Im Intervall \((0,\infty)\) bestizt die Funktion eine Linkskrümmung. Zusammenfassend können wir sagen:
Im Intervall \((-\infty,0)\) liegt eine Rechtskrümmung vor und im Intervall \((0,\infty)\) liegt eine Linkskrümmung vor. An dem Sattelpunkt \(x=0\) findet der Übergang zwischen den zwei Krümmungen statt.