Wendepunkt berechnen
Wendepunkt Rechner
Der Online Rechner von Simplexy kann dir bei der Wendepunkt Berechnung sehr helfen. Mit dem Rechner kannst du dir den Graphen einer Funktion zeichnen lassen, die Funktion ableiten und viel mehr.
Wendepunkte berechnen - Kurvendiskussion
Bei einem Wendepunkt handelt es sich um einen Punkt, bei dem der Funktionsgraph seine Krümmung ändert.
1. Notwendige Bedingung:
\(f''(x_W)=0\,\,\implies\,\,\)potentielle Wendestelle bei \(x_W\)
2. Hinreichende Bedingung:
\(f''(x_W)=0\) und \(f'''(x_W)\ne 0\)
- \(f'''(x_W)\lt 0\,\,\implies\,\,\) Links-rechts-Wendestelle
- \(f'''(x_W)\gt 0\,\,\implies\,\,\) Rechts-links-Wendestelle
An einem Wendepunkt besitzt eine Funktion (mindestens lokal) die größte Steigung. In Aufgabenstellungen wird daher oft nach dem Punkt mit der stärksten Zunahme bzw. Abnahme gefragt.
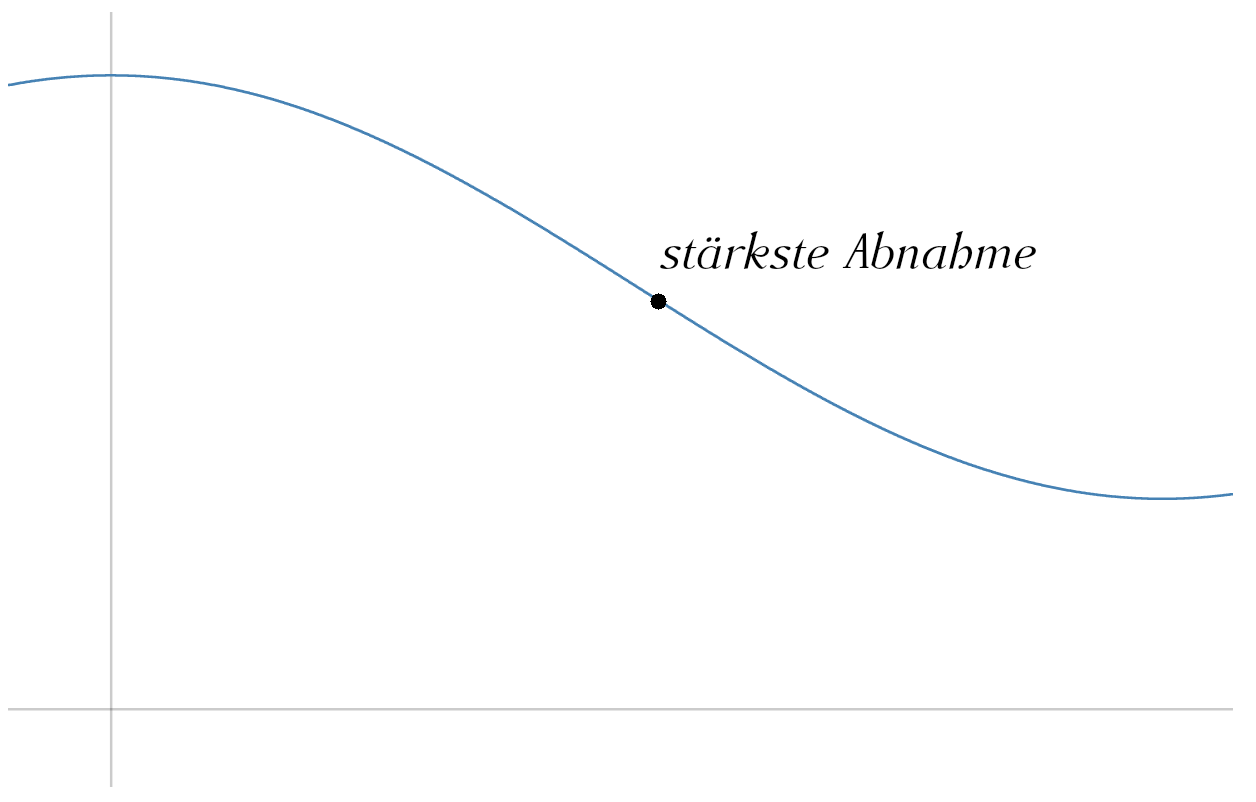
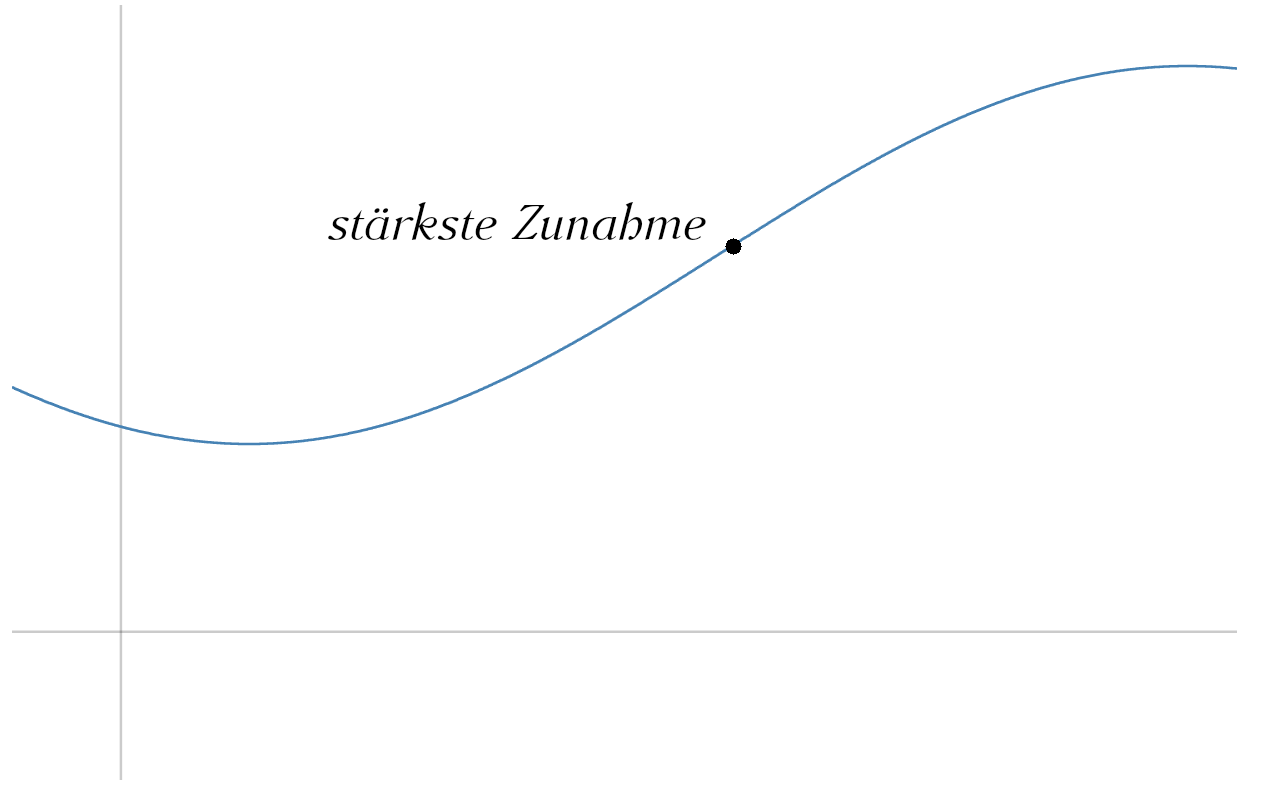
Bedingungen für das Ermitteln von einem Wendepunkt
1. Notwendige Bedingung:
- \(f''(x_W)=0\,\,\implies\,\,\) potentieller Wendepunkt
2. Hinreichende Bedingung:
- \(f''(x_W)=0\) und \(f'''(x_W)\ne 0 \,\,\implies\,\,\) Wendepunkt
Beispiel Aufgabe Wendepunkt berechnen:
Untersuche die folgende Funktion nach Wendepunkten:
\(f(x)=\frac{1}{4}x^3-\frac{3}{2}x^2+3x-1\)
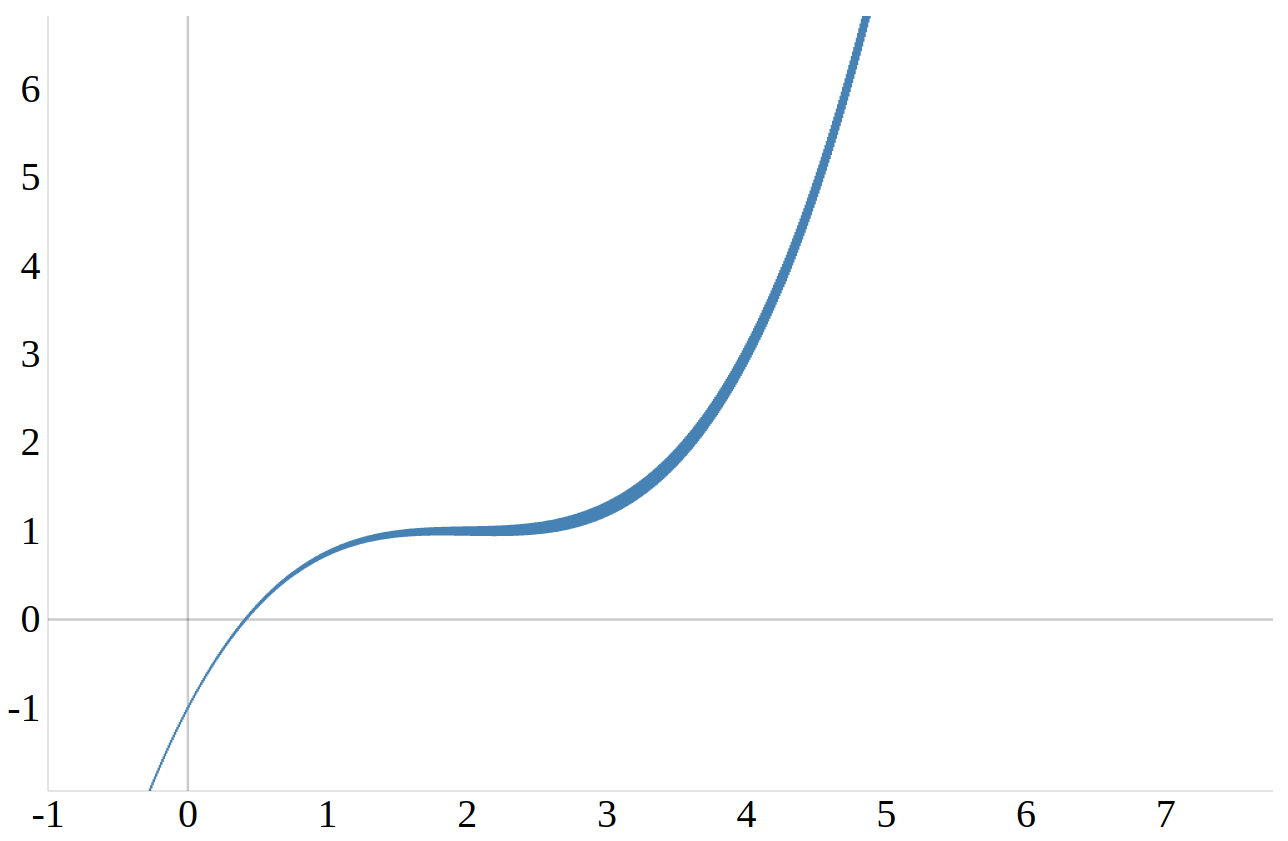
Schritt 1 - Berechne die zweite Ableitung und setze sie gleich Null:
\(f'(x)=\frac{3}{4}x^2-3x+3\)
\(f''(x)=\frac{3}{2}x-3=0\)
Löst man die Nullstellen der zweiten Ableitung, dann erhält man als potentiellen Wendestelle:
\(x_W=2\)
Schritt 2 - Berechne die dritte Ableitung und setze \(x_W\) ein:
\(f'''(x)=\frac{3}{2}\)
Da die dritte Ableitung unabhängig von \(x\) ist, können wir da nix einsetzten. Trotzdem ist \(f'''(x)=\frac{3}{2}\gt 0\), dass heißt, \(x_W=2\) ist eine Wendestelle. Um genau zu sein handelt es sich um eine Rechts-links-Wendestelle.
Um den Funktionswert bei der Wendestelle zu ermitteln, setzen wir \(x_W\) in die Funktion ein und erhalten:
\(f(x_W)=\frac{1}{4}\cdot 2^3-\frac{3}{2}\cdot 2^2+3\cdot 2-1=1\)
Die Funktion besitzt am Punkt \(P(2|1)\) eine Rechts-links-Wendestelle.
Arten von Wendepunkten
Wie bereits erwähnt unterscheidet man zwischen einem Rechts-links-Wendepunkt und einem Links-rechts-Wendepunkt. Dabei handelt es sich um eine Bezeichnung um klarzustellen ob erst die Links- oder erst die Rechts-Kurve kommt.
Wendepunkt arten
- \(f'''(x_W)\lt 0\,\,\implies\,\,\) Links-rechts-Wendestelle
- \(f'''(x_W)\gt 0\,\,\implies\,\,\) Rechts-links-Wendestelle
