Bestimmtes und unbestimmtes Integral
Integral Rechner
Der Integral Rechner von Simplexy kann dir das bestimmte und unbestimmte Integral berechnen und noch viel mehr. Probiere den Integralrechner aus...
Bestimmtes und unbestimmtes Integral einfach erklärt
Sowohl das bestimmte Integral als auch das unbestimmte Integral sind wichtige Bestandteile der Integralrechnung
Der Unterschied zwischen einem bestimmten und einem unbestimmten Integral liegt zum einen in der Schreibweise und zum anderen in der Anwendung.
Das unbestimmte Integral
\(\displaystyle\int f(x)\,\,dx\)
Das unbestimmte Integral wird verwendet, wenn eine Stammfunktion gesucht ist. Dabei ist es wichtig zu wissen, dass es zu einer Funktion \(f(x)\) unendlich viele Stammfunktionen gibt.
Unbestimmtes Integral
Die Menge aller Stammfunktionen wird unbestimmtes Integral genannt.
Bestimmtes Integral
Das bestimmte Integral wird mit Integrationsgrenzen geschrieben.
\(\displaystyle\int_{\color{blue}{a}}^{\color{blue}{b}} f(x)\,\,dx\)
Ein bestimmtes Integral berechnen liefert also immer eine konkrete Zahl. Diese Zahl gibt dir den Flächeninhalt zwischen einem Graphen und der x-Achse im Intervall \([\color{blue}{a},\color{blue}{b}]\) an.

Um das bestimmte Integral berechnen zu können wird die Stammfunktion ebenfalls benötigt. Mehr dazu im nächsten Absatz.
Bestimmtes Integral berechnen
Wie man ein bestimmtes Integral berechnen kann, werden wir direkt an einem Beispiel zeigen. Berechne das folgende bestimmte Integral:
\(\displaystyle\int_{\color{green}{1}}^{\color{blue}{3}} x\,\,dx\)
Schritt 1
Berechne die Stammfunktion \(F(x)\)
\(F(x)=\frac{1}{2}x^2\)
Schritt 2
Deute an, dass du die Integrationsgrenzen in die Stammfunktion einsetzen wirst. Dies machst du mit Hilfe von eckigen Klammern.
\(\displaystyle\int_{\color{green}{1}}^{\color{blue}{3}} x\,\,dx=\Bigg[F(x)\Bigg]_{\color{green}{1}}^{\color{blue}{3}}=\Bigg[\frac{1}{2}x^2\Bigg]_{\color{green}{1}}^{\color{blue}{3}}\)
Schritt 3
Nun kannst du das bestimmte Integral berechnen indem du das folgende ausrechnest:
\(F({\color{blue}{3}})-F({\color{green}{1}})\)
also \(F({\color{blue}{\text{obere Grenze}}})\) minus \(F({\color{green}{\text{untere Grenze}}})\)
\(\begin{aligned} \displaystyle\int_{\color{green}{1}}^{\color{blue}{3}} x\,\,dx&=\Bigg[\frac{1}{2}x^2\Bigg]_{\color{green}{1}}^{\color{blue}{3}}\\ \\ &=\big(\frac{1}{2}{\color{blue}{3}}^2\big)-\big(\frac{1}{2}{\color{green}{1}}^2\big)\\ \\ &=\frac{9}{2}-\frac{1}{2}=4 \end{aligned}\)
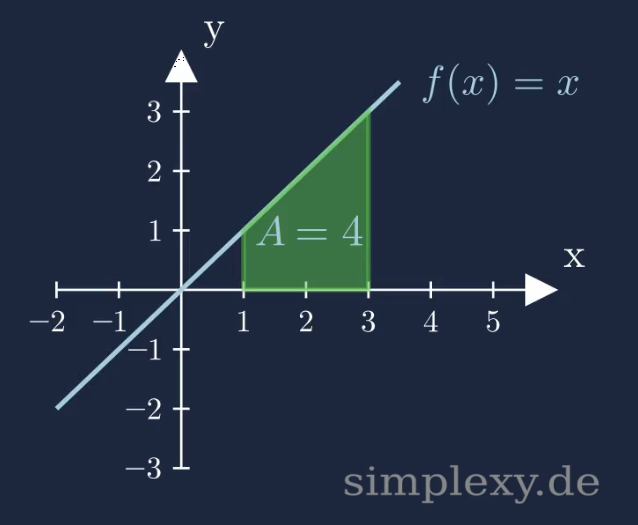
Das bestimmte Integral ist ein Bestandteil des Hauptsatz der Differential- und Intagralrechnung. Die allgemeine Formel lautet:
Bestimmtes Integral berechnen
\(\displaystyle\int_{\color{green}{a}}^{\color{blue}{b}} f(x)\,\,dx=\Big[F(x)\Big]_{\color{green}{a}}^{\color{blue}{b}}=F({\color{blue}{b}})-F({\color{green}{a}})\)
Beispiel bestimmtes Integral berechnen
Berechne das folgende bestimmte Integral:
\(\displaystyle\int_{\color{green}{-1}}^{\color{blue}{1}} x^2\,\,dx\)
Schritt 1
Berechne die Stammfunktion \(F(x)\)
\(F(x)=\frac{1}{3}x^3\)
Schritt 2
Deute an, dass du die Integrationsgrenzen in die Stammfunktion einsetzen wirst. Dies machst du mit Hilfe von eckigen Klammern.
\(\displaystyle\int_{\color{green}{-1}}^{\color{blue}{1}} x^2\,\,dx=\Bigg[F(x)\Bigg]_{\color{green}{-1}}^{\color{blue}{1}}=\Bigg[\frac{1}{3}x^3\Bigg]_{\color{green}{-1}}^{\color{blue}{1}}\)
Schritt 3
Nun kannst du das bestimmte Integral berechnen indem du das folgende ausrechnest:
\(F({\color{blue}{1}})-F({\color{green}{-1}})\)
also \(F({\color{blue}{\text{obere Grenze}}})\) minus \(F({\color{green}{\text{untere Grenze}}})\)
\(\begin{aligned} \displaystyle\int_{\color{green}{-1}}^{\color{blue}{1}} x^2\,\,dx&=\Bigg[\frac{1}{3}x^3\Bigg]_{\color{green}{-1}}^{\color{blue}{1}}\\ \\ &=\frac{1}{3}{\color{blue}{1}}^3-\frac{1}{3}{\color{green}{(-1)}}^3\\ \\ &=\frac{1}{3}-(-\frac{1}{3})=\frac{2}{3} \end{aligned}\)
Besonderheiten - Bestimmtes Integral berechnen
Um eine wichtige Besonderheit des bestimmten Integrals zu verdeutlichen, rechnen wir noch ein weiteres Beispiel.
Wir betrachten die Funktion \(sin(x)\) und möchten die Fläche zwischen dem Graphen und der x-Achse im Intervall \([-\pi,\pi]\) berechnen.
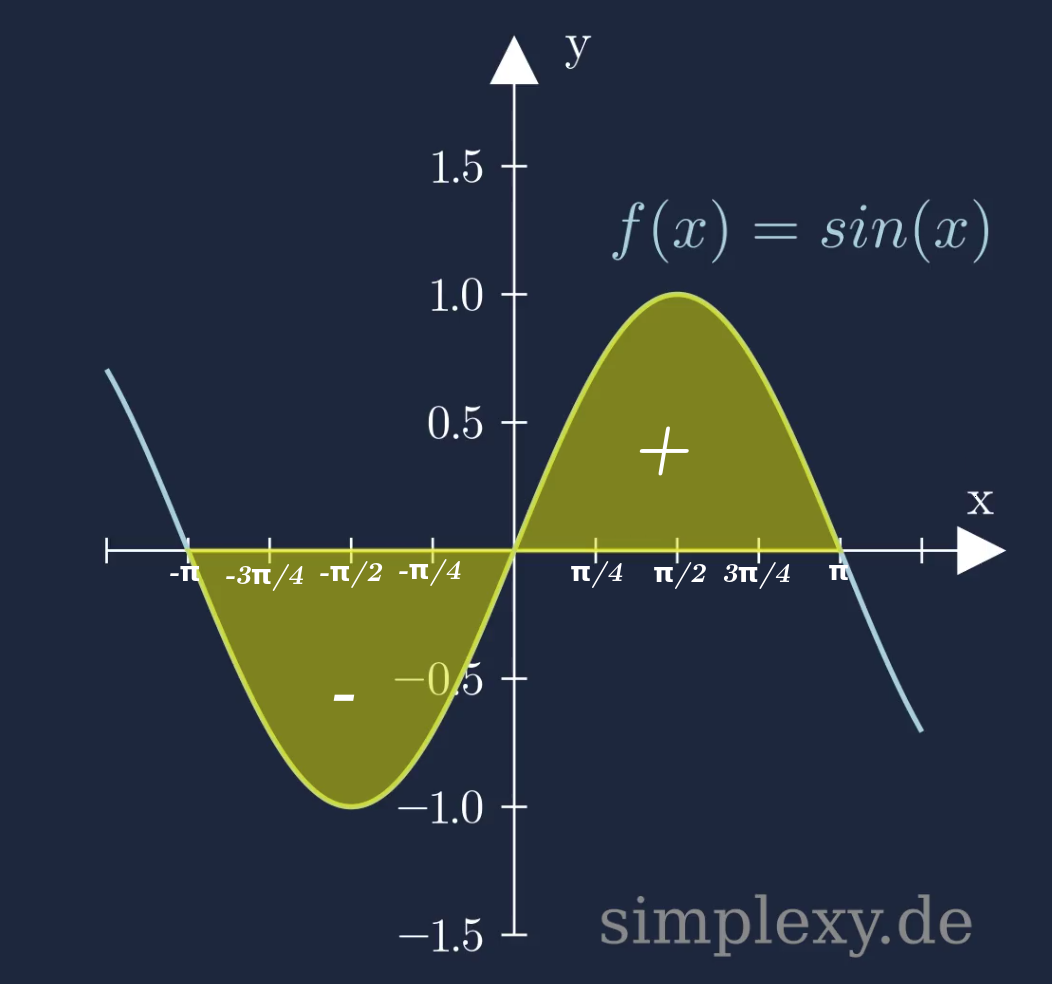
Die Fläche erhält man über das bestimmte Integral
\(\displaystyle\int_{-\pi}^{\pi} sin(x)\,\,dx\)
Um dieses bestimmte Integral zu berechnen nutzen wir die gleichen Schritte wie in den letzten beiden Beispielen.
Schritt 1
Berechne die Stammfunktion \(F(x)\)
\(F(x)=-cos(x)\)
Schritt 2
Deute an, dass du die Integrationsgrenzen in die Stammfunktion einsetzen wirst. Dies machst du mit Hilfe von eckigen Klammern.
\(\begin{aligned} \displaystyle\int_{\color{green}{-\pi}}^{\color{blue}{\pi}} sin(x)\,\,dx&=\bigg[F(x)\bigg]_{\color{green}{-\pi}}^{\color{blue}{\pi}}\\ \\ &=\big[-cos(x)\big]_{\color{green}{-\pi}}^{\color{blue}{\pi}} \end{aligned}\)
Schritt 3
Nun kannst du das bestimmte Integral berechnen indem du das folgende ausrechnest:
\(F({\color{blue}{\pi}})-F({\color{green}{-\pi}})\)
also \(F({\color{blue}{\text{obere Grenze}}})\) minus \(F({\color{green}{\text{untere Grenze}}})\)
\(\begin{aligned} \displaystyle\int_{\color{green}{-\pi}}^{\color{blue}{\pi}} sin(x)\,\,dx&=\Bigg[-cos(x)\Bigg]_{\color{green}{-\pi}}^{\color{blue}{\pi}}\\ \\ &=-cos({\color{blue}{\pi}})-\big(-cos({\color{green}{-\pi}})\big)\\ \\ &=1-1=0 \end{aligned}\)
Nun stellt sich die Frage warum das bestimmte Integral gleich null ist, obwohl die Fläche ungleich Null ist.
Dies ist zurück zu führen auf eine wichtige Besonderheit des bestimmten Integrals.
Besonderheit bestimmtes Integral berechnen
Das bestimmte Integral liefert positive und negative Werte.
An dem Beispiel mit der Sinus-Funktion sieht man, der Flächeninhalt zwischen dem Graph und der x-Achse lässt sich nicht so leicht berechnen, wenn die Funktion innerhalb der Integrationsgrenzen sowohl unterhalb als auch oberhalb der x-Achse verläuft. In solchen Fällen muss man das bestimmte Integral aufteilen. Dabei wird das bestimmte Integral so aufgeteilt, dass man von einer Nullstelle der Funktion zur nächsten Nullstelle integriert und die Beträge davon werden addiert. Am beispiel der Sinus-Funktion geht man also wie folgt vor um die Fläche A zwischen dem Graphen und x-Achse zu berechnen.
\(\begin{aligned} A&=\Bigg|\displaystyle\int_{-\pi}^{0} sin(x)\,\,dx\Bigg|+\Bigg|\displaystyle\int_{0}^{\pi} sin(x)\,\,dx\Bigg|\\ \\ &=\Bigg|\Big[-cos(x)\Big]_{-\pi}^{0}\Bigg|+\Bigg|\Big[-cos(x)\Big]_{0}^{\pi}\Bigg|\\ \\ &=\Big|-cos(0)+cos(-\pi)\Big|+\Big|-cos(\pi)+cos(0)\Big|\\ \\ &=2+2=4 \end{aligned}\)
Damit ist die Fläche zwischen dem Graphen der Funktion \(f(x)=sin(x)\) und der x-Achse im Intervall \([-\pi,\pi]\) genau \(4\) Flächeneinheiten groß.
Das bestimmte Integral besitzt weitere Besonderheit...
Bestimmtes Integral Summenregel
Wenn man ein bestimmtes Integral berechnen möchte, so kann man oft die Summenregel anwenden. Diese kommt zum Einsatz, wenn man zwei Integrale mit denselben Integrationsgrenzen zusammenfassen will.
Summenregel bestimmtes Integral berechnen
\(\displaystyle\int_a^b f(x)\,\,dx+\displaystyle\int_a^b g(x)\,\,dx=\displaystyle\int_a^b f(x)+g(x)\,\,dx\)
Integrationsgrenzen zusammenfassen
Die folgende Regel für ein bestimmtes Integral ist ebenfalls sehr hilfreich
Zusammenfassen von Integrationsgrenzen
\(\displaystyle\int_a^b f(x)\,\,dx+\displaystyle\int_b^c f(x)\,\,dx=\displaystyle\int_a^c f(x)\,\,dx\)
Vertauschen von Integrationsgrenzen
Bei einem bestimmten Integral kann man die Integrationsgrenzen vertauschen. Dabei entsteht jedoch ein Vorzeichenwechsel.
Vertauschte Integrationsgrenzen beim bestimmten Integral
\(\displaystyle\int_a^b f(x)\,\,dx=-\displaystyle\int_b^a f(x)\,\,dx\)
Bestimmtes Integral mit gleichen Integrationsgrenzen
Ein bestimmtes Integral mit gleichen Integrationsgrenzen ist gleich Null.
Gleiche Integrationsgrenzen
\(\displaystyle\int_a^a f(x)\,\,dx=0\)
Diese Besonderheit des bestimmten Integrals sind oftmals sehr hilfreich, es lohnt sich diese zu merken. Im nächsten Abschnitt geht es damit weiter, was ein unbestimmtes Integral ist.
Unbestimmtes Integral
Der Unterschied zwischen einem bestimmten Integral und einem unbestimmtes Integral liegt darin, dass das unbestimmte Integral keine Integrationsgrenzen bestizt.
\(\displaystyle\int f(x)\,\,dx\)
Unbestimmtes Integral
Man nennt die Menge aller Stammfunktionen einer Funktion \(f(x)\) unbestimmtes Integral.
Das unbestimmte Integral wird als Menge aller Stammfunktionen bezeichnet, weil man zu einer Funktion stets unendlich viele Stammfunktionen finden kann.
unbestimmtes Integral berechnen Beispiel
Das unbestimmte Integral der Funktion \(f(x)=3x\) wird wie folgt geschrieben:
\(\displaystyle\int x\,\,dx=\frac{1}{2}x^2+C\)
Wir wissen, dass wenn man die Stammfunktion \(F(x)\) ableitet, so erhält man die Funktion \(f(x)\). Bei der Funktion \(f(x)=x\) lautet die Stammfunktion \(F(x)=\frac{1}{2}x^2\). Eine weitere Stammfunktion wäre auch
\(\frac{1}{2}x^2+{\color{blue}{1}}\)
oder
\(\frac{1}{2}x^2+{\color{blue}{5}}\)
Da die Konstante beim ableiten wegfällt, sind die funktionen \(\frac{1}{2}x^2+{\color{blue}{1}}\) und \(\frac{1}{2}x^2+{\color{blue}{5}}\) Stammfunktionen der Funktion \(f(x)=x\).
Die Konstante
Eine Stammfunktion kann immer mit einer Konstante addiert oder subtrahiert werden und es wäre dann immernoch eine Stammfunktion. Jede Stammfunktion von \(f(x)=x\) kann daher allgemein wie folgt geschrieben werden:
\(F(x)=\frac{1}{2}x^2+C\)
Dabei ist \(C\) eine beliebige Zahl (Konstante).
Allgemein kann ein unbestimmtes Integral geschrieben werden als:
\(\displaystyle\int f(x)\,\,dx=F(x)+C\)

Unbestimmtes Integral berechnen Beispiele
Wie du mittlerweile weißt, können wir ein unbestimmtes Integral berechnen indem wir die Stammfunktion angeben. Dazu muss man jedoch wissen wie man eine Stammfunkion berechnen kann. Je nach Funktion muss man verschiedene Integrationsregeln anwenden um auf die Stammfunktion zu kommen. Diese Regeln haben wir hier bereits erläutert, daher betrachten wir jetzt direkt einige Beispiele, wie man ein unbestimmtes Integral berechnen kann.
Beispiel 1: Unbestimmtes Integral
Gegeben ist die Funktion
\(f(x)=-x^3+2x+4\)
Du sollst nun das unbestimmte Integral berechnen, also:
\(\displaystyle\int -x^3+2x+4\,\,dx\)
Dafür musst du die Stammfunktion ermitteln. Diese lautet:
\(\displaystyle\int -x^3+2x+4\,\,dx=-\frac{1}{4}x^4+x^2+4x+C\)
Du darfst die Konstante C nicht vergessen. Solltest du nach einer konkreten Stammfunktion suchen, so kannst du die Konstante \(C\) mit einer beliebigen Zahl ersetzen.
Beispiel 2: Unbestimmtes Integral
Gegeben ist die Funktion
\(f(x)=e^x\)
Du sollst nun das unbestimmte Integral berechnen, also:
\(\displaystyle\int e^x\,\,dx\)
Dafür musst du zunächst die Stammfunktion ermitteln. Da die Ableitung der e-Funktion wieder die e-Funktion ergibt, muss die Stammfunktion der e-Funktion ebenfalls eine e-Funktion sein.
\(\displaystyle\int e^x\,\,dx=e^x+C\)
Beispiel 3: Unbestimmtes Integral
Gegeben ist die Funktion
\(f(x)=\sqrt{x}\)
Wie lautet die Stammfunktion?
\(\displaystyle\int \sqrt{x}\,\,dx\)
Um das unbestimmte Integral der Wurzelfunktion zu berechnen, muss du raus finden wie die Stammfunktion von \(\sqrt{x}\) lautet. In dem Beitrag zur Stammfunktion der Wurzelfunktion wurde dies bereits erklärt. Daher kommt nun eine Kurzfassung.
Den Ausdruck \(\sqrt{x}\) kann man in eine Potenzfunktion umschreiben:
\(\sqrt{x}=x^{\frac{1}{2}}\)
Damit kann man also nun die Potenzregel anwenden um die Stammfunktion der Wurzelfunktion zu ermitteln.
\(\displaystyle\int \sqrt{x}\,\,dx=\displaystyle\int x^{\frac{1}{2}}\,\,dx=\frac{2}{3}x^{\frac{3}{2}}+C\)
Weitere Beispiele
| f(x) | F(x) |
| \(e^{-x}\) | \(-e^{-x}\) |
| \(3e^{3x}+1\) | \(e^{3x}+x\) |
| \(e^{2x}\) | \(\frac{1}{2}\)\(e^{2x}\) |
| \(e^{-2x}\) | \(-\frac{1}{2}\)\(e^{-2x}\) |
| \(\frac{1}{x}\) | \(ln(x)\) |
| \(\frac{1}{x^2}\) | \(-\frac{1}{x}\) |
| \(sin(x)\) | \(-cos(x)\) |
| \(cos(x)\) | \(sin(x)\) |
