Integralrechnung
Integralrechner
Der Integralrechner von Simplexy kann beliebige Funktionen für dich integrieren und aufleiten. Berechne ganz simple die Stammfunktion und die Flächen unter einem Graphen.
Integralrechnung
Neben der Differentialrechnung ist die Integralrechnung eines der Hauptthemen in der Analysis. Die Integration ist die Umkehrung der Ableitung und wird in der Schule meist dafür benutzt Flächen unter einem Graphen zu berechnen. Das Wort Integral ist ein Oberbegriff für das "bestimmte Integral" und "unbestimmte Integral". Im Folgenden wirst du die Grundlagen der Integralrechnung und die wichtigen Integralregeln lernen, desweiteren wirst du sehen wie man die Fläche unter einem Graphen berechnet.
Grundlagen der Integralrechnung
Wie bereits erwähnt ist das Integrieren einer Funktion die Umkehrung der Ableitung, wesshalb man zum integrieren auch "Aufleiten" sagt.
\(\underbrace{F(x)}_{\text{Stammfunktion}}\overbrace{\leftarrow}^{\text{integrieren}} f(x)\overbrace{\rightarrow}^{\text{ableiten}} \underbrace{f'(x)}_{\text{1.Ableitung}}\)
Wenn man eine funktion \(f(x)\) integriert (aufleitet), erhält man die sogenannte Stammfunktion \(F(x)\). Leitet man die Stammfunktion ab dann erhält man die Ausgangsfunktion.
\(F'(x)=f(x)\)
In der Folgenden Tabelle sind einige typische Potenzfunktionen und ihre Stammfunktionen eingetragen.
| f(x) | F(x) |
| \(1\) | \(x\) |
| \(4\) | \(4\cdot x\) |
| \(x\) | \(\frac{1}{2}\)\(x^2\) |
| \(x^2\) | \(\frac{1}{3}\)\(x^3\) |
| \(2\cdot x^5\) | \(\frac{2}{6}\)\(x^6\) |
| \(x^2-4\) | \(\frac{1}{3}\)\(x^3-4\cdot x\) |
Wie dir womöglich aufgefallen ist, integriert man eine Potenzfunktion indem man den Exponenten um \(1\) erhöht und in den Nenner schreibt.
Regel:
Integration von Potenzfunktionen
Die Stammfunktion zu der Pontenzfunktion
\(f(x)=x^n\)\(\,\,\,\,\,\,\,\,n\in\natnums\)
berechnet sich über:
\(F(x)=\)\(\frac{1}{n+1}\)\(x^{n+1}\)
Beispiel
Berechne die Stammfunktion von
\(f(x)=x^2+2x-1\)
Wir wenden die Regel zur Integration von Potenzfunktionen an und erhalten:
\(\begin{aligned} F(x)&=\frac{1}{3}x^3+\frac{2}{2}x^2-x\\ \\ &=\frac{1}{3}x^3+x^2-x \end{aligned}\)
Um zu überprüfen ob wir richtig integriert haben, müssen wir die Stammfunktion ableiten und sollten die Ursprungsfunktion erhalten. Das liegt daran, weil das Ableiten die Umkehrung der Integration ist.
\(\begin{aligned} F'(x)&=\Big(\frac{1}{3}x^3+x^2-x\Big)'\\ \\ &=\frac{3}{3}x^2+2x-1\\ \\ &=x^2+2x-1 \end{aligned}\)
Wie du siehst haben wir die Stamfunktion korrekt ermittelt.
Bemerkung
Wir hätten zu unserer Stammfunktion eine Beliebige Konstante addieren können ohne dabei eine falsche Stammfunktion zu bekommen.
\(\begin{aligned} F(x)&=\frac{1}{3}x^3+x^2-x+\underbrace{10}_\text{Konstante} \end{aligned}\)
Denn die Ableitung von \(F(x)\) mit der Konstanten würde immer noch zu unserer Ausgangsfunktion führen. Das liegt daran, dass die Konstante beim ableiten wegfällt.
Denn
\(10'=0\)
Allgemein schreibt man die Konstante in der Stammfunktion folgendermaßen:
\(\begin{aligned} F(x)=\frac{1}{3}x^3+x^2-x+C \end{aligned}\)
Der einfachheithalber lässt man die Konstante oft weg bzw. man setzt.
\(C=0\)
Solche Funktion kannst du mit dem Integralrechner leicht integrieren. Probiere den Rechner aus!
Weitere typische stammfunktionen
| f(x) | F(x) |
| \(e^x\) | \(e^x\) |
| \(3e^{3x}\) | \(e^{3x}\) |
| \(e^{2x}\) | \(\frac{1}{2}\)\(e^{2x}\) |
| \(e^{-2x}\) | \(-\frac{1}{2}\)\(e^{-2x}\) |
| \(\frac{1}{x}\) | \(ln(x)\) |
| \(\frac{1}{x^2}\) | \(-\frac{1}{x}\) |
| \(sin(x)\) | \(-cos(x)\) |
| \(cos(x)\) | \(sin(x)\) |
Das Integrieren von Funktionen ist aufwendiger als das Ableiten. Um eine Funktion abzuleiten muss man lediglich die Ableitungregeln stupide anwenden, dass Integrieren ist aufwendiger weil es nicht immer eine Regel gibt die man anwenden kann. Wenn man die Stammfunktion einer Funktion sucht dann hilft es, sich die Frage zu stellen:
Welche Funktion muss ich Ableiten damit meine Ausgangsfunktion bei rauskommt?
Du solltest immer eine Probe machen und deine Stammfunktion ableiten, um zu sehen ob du die Ausgangfunktion erhälts.
Probiere den Integralrechner aus um verschiedene Funktion zu integrieren.
Unbestimmtes Integral
Das Unbestimmte Integral ist eine mathematische Schreibweise mit der man zum Ausdruck bringt, dass man die Stammfunktion einer Ausgangsfunktion \(f(x)\) sucht. Man schreibt:
\(\displaystyle\int f(x)\,\,\,dx=F(x)+C\)
Das zeichen \(\displaystyle\int\) ist einfach nur ein mathematisches Zeichen um klar zu machen das man integrieren möchte. \(f(x)\) ist die Funktion von der man gerne die Stammfunktion berechnen möchte und das Zeichen \(dx\) gibt einem vor, nach welcher Variable man integrieren möchte. Das zeichen \(dx\) sagt einem von welcher Variable die Funktion \(f\) abhängt.
Eine Variable ist nur eine Platzhalter. Eine Funktion kann beispielsweiße auch von \(y\) abhängen, dann würde man schreiben:
\(\displaystyle\int f(y)\,\,\,dy=F(y)+C\)
In diesem Fall ist die Integrationsvariable \(y\), weshalb man \(dy\) schriebt.
Beispiele:
- \(\displaystyle\int\,1\,\,\,dx=x+C\)
- \(\displaystyle\int\,x\,\,\,dx=\)\(\frac{1}{2}\)\(x^2+C\)
- \(\displaystyle\int\,3\cdot y^2\,\,\,dy=\)\(y^3+C\)
- \(\displaystyle\int\,e^{2x}\,\,\,dx=\)\(\frac{1}{2}\)\(e^{2x}+C\)
Bestimmtes Integral
Sind Integrationsgrenzen angegeben, dann handelt es sich um ein Bestimmtes Integral. Mit einem Bestimmten Integral kann man die Fläche unter der Funktion \(f(x)\) berechnen, die von den Integrationsgrenzen aufgespannt wird. Gelöst wird ein bestimmtes Integral mit dem Hauptsatz der Integral- und Differentialrechnung.
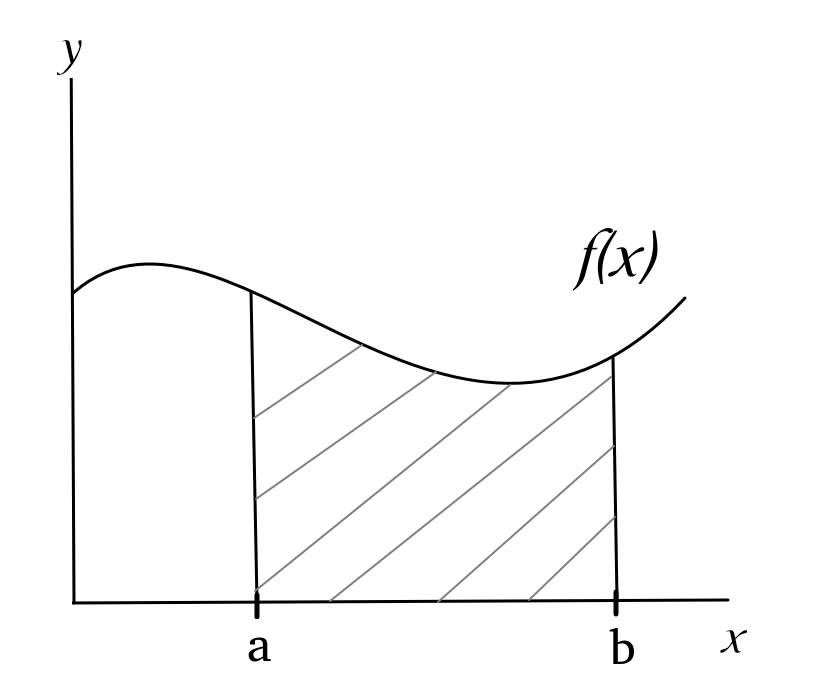
Mathematisch wird ein bestimmtes Integral folgendermaßen geschrieben:
\(\displaystyle\int^{b}_{a} f(x)\,\,\,dx=[F(x)]^{b}_{a}=F(b)-F(a)\)
Flächenberechnung mit Integralen
Beispiel 1
Wie groß ist die Fläche die vom Graphen der
Funktion \(f(x)=-(x-3)^2+4\) und der \(x\)-Achse im Intervall \([1,5]\) eigeschlossen wird?
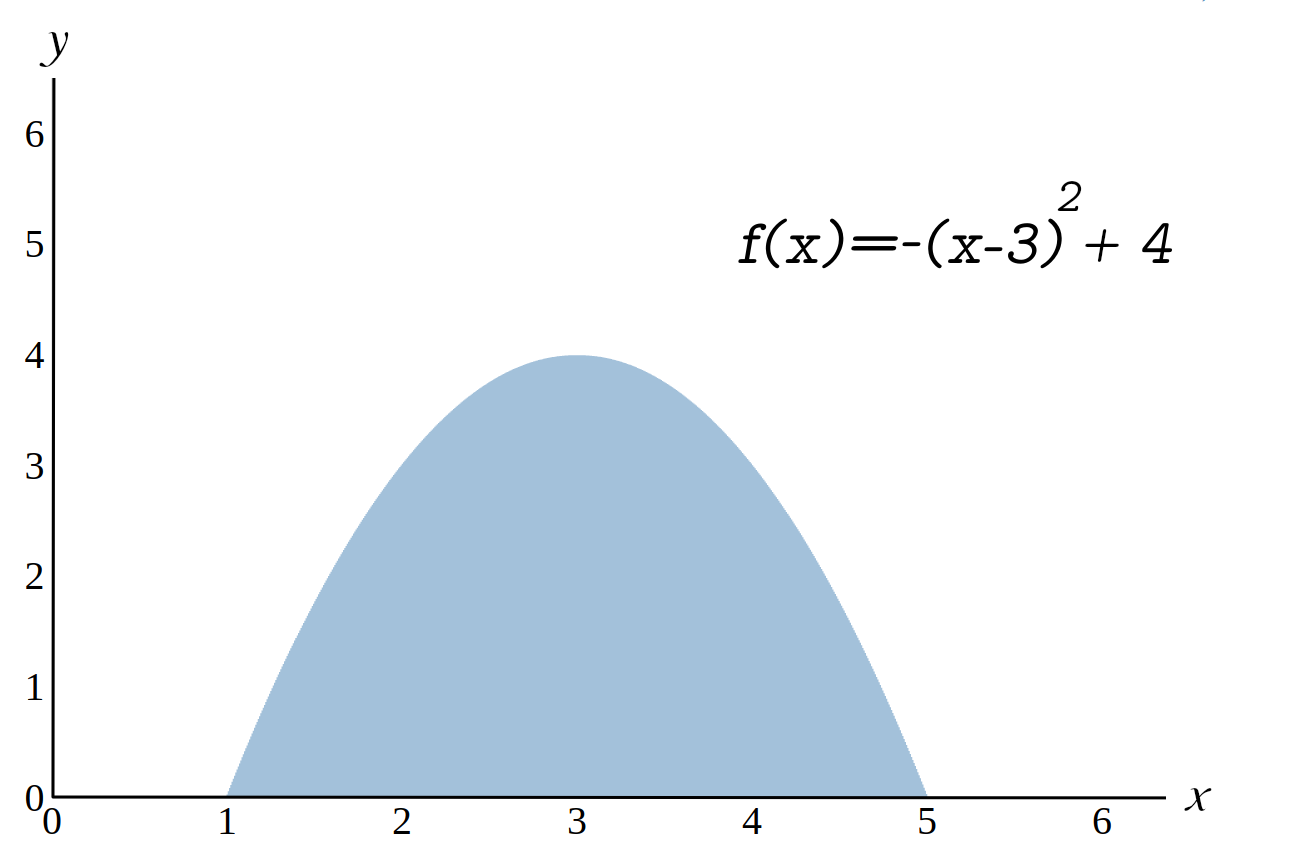
Lösung
Die Fläche unter dem Graphen berechnet sich über:
\(\displaystyle\int^{5}_{1} -(x-3)^2+4\,\,\,dx=\)\(\Big[-\)\(\frac{1}{3}\)\(x^3+3x^2-5x\Big]^{5}_{1}\)
\(\,\,=\Big(\)\(-\frac{1}{3}\)\(5^3+3\cdot 5^2-5\cdot 5\Big)-\)\(\Big(\)\(-\frac{1}{3}\)\(1^3+3\cdot 1^2-5\cdot 1\Big)\)
\(\,\,=8,33+2,33=10,66\,\,FE\)
Die Fläche unter dem Graphen im Intervall \([1,5]\) ist
\(10,66\) Flächeneinheiten groß
So ein bestimmtes Integral kannst du auch mit Online Integralrechner mit Grenzen von Simplexy berechnen.
Hier kommst du zum Integralrechner.
Beispiel 2
Berechne die Fläche, die vom Graphen der Funktion
\(f(x)=-x^2+1\) und der \(x\)-Achse eingeschlossen wird.
Lösung
Zunächst müssen wir die Integrationsgrenzen bestimmten. Da wir die Fläche zwischen dem Graphen und der \(x\)-Achse berechnen sollen, sind die Integrationsgrenzen gerade die Nullstellen der Funktion.
Mit der pq-Formel berechnen wir die Nullstellen von
\(f(x)=-x^2+1\) und erhalten:
\(x_1=-1\) und \(x_2=1\)
Die Fläche unter dem Graphen erhalten wir über das bestimmte Integral
\(\displaystyle\int^{1}_{-1} -x^2+1\,\,\,dx=[-\frac{1}{3}x^3+x]^{1}_{-1}=\frac{2}{3}+\frac{2}{3}=\frac{4}{3}\)
Die Fläche zwischen dem Graphen und der \(x\)-Achse beträgt \(\frac{4}{3}\) Flächeneinheiten.
Beispiel 3
Bestimme die Fläche zwischen dem Graphen der Funktion
\(f(x)=x^3\) und der \(x\)-Achse im Intervall \([-1,1]\).
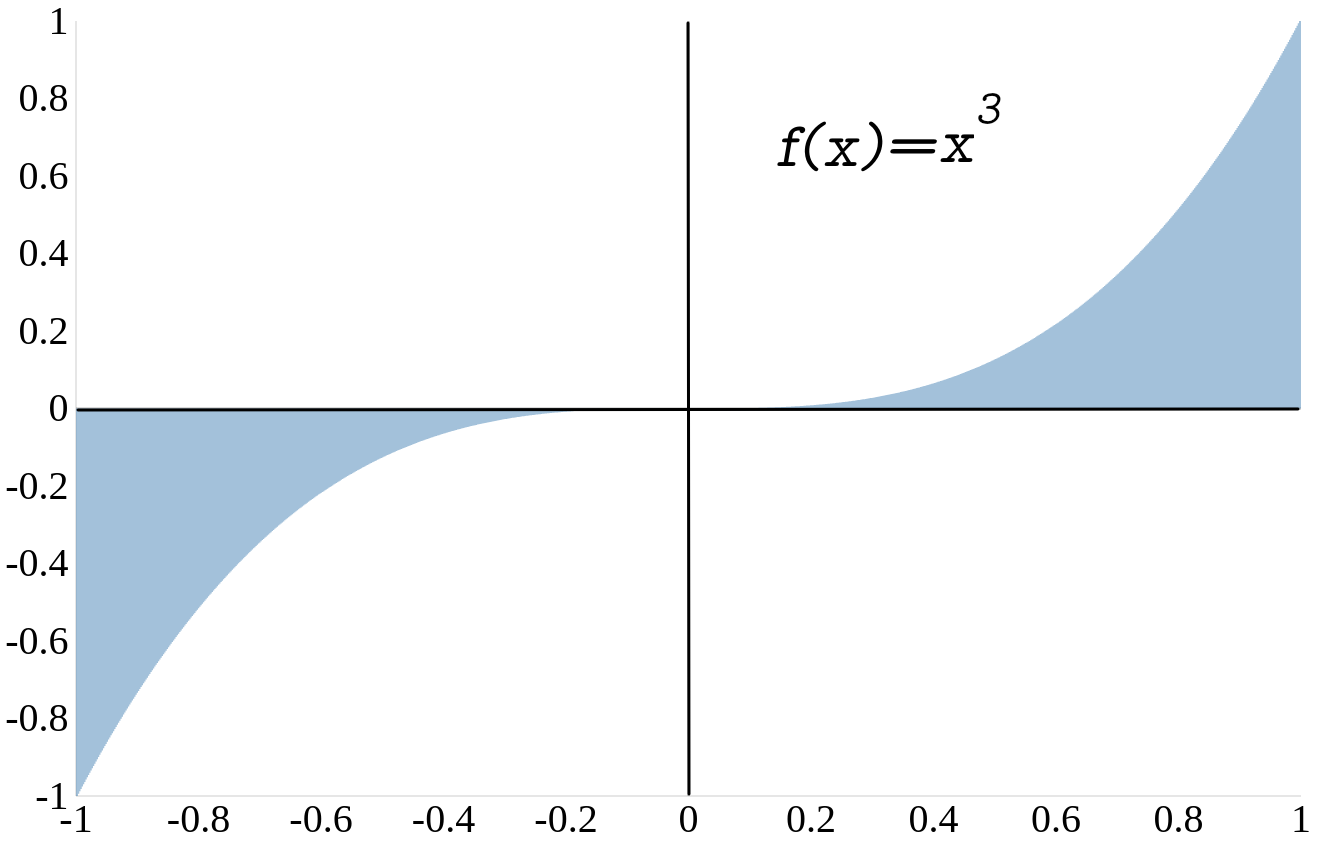
Lösung
Um die Fläche unter dem Graphen zu erhalten müssen wir folgendes Integral lösen:
\(\displaystyle\int^{1}_{-1} x^3\,\,\,dx\)
Achtung !
Liegt der Funktionsgraph in einem bestimmten Intervall unterhalb der \(x\)-Achse, so liefert das bestimmte Integral in diesem Intervall eine negative Zahl. Ist nach der Fläche gefragt so nimmt man in diesem Intervall den Betrag des Integrals, denn eine Fläche ist immer Positiv.
Da der Graph von \(f(x)=x^3\) im Intervall \([-1,0]\) unterhalb der \(x\)-Achse liegt, müssen wir unser Integral in zwei Integrale aufteilen.
\(\displaystyle\int^{1}_{-1} x^3\,\,\,dx=\displaystyle\int^{0}_{-1} x^3\,\,\,dx+\displaystyle\int^{1}_{0} x^3\,\,\,dx\)
Da die Funktion im Intervall \([-1,0]\) unterhalb der \(x\)-Achse liegt, wird das Integral über dieses Intervall eine negative Zahl liefern. Eine Fläche muss aber einen Positiven Wert haben, deshalb muss man den Betrag der Zahl nehmen.
\(\displaystyle\int^{0}_{-1} x^3\,\,\,dx=\big[\frac{1}{4}x^4\big]_{-1}^{0}=-\frac{1}{4}\)
Die Fläche zwischen \(x\)-Achse und der Funktion im Intervall \([-1,0]\) beträgt
\(|-\frac{1}{4}|=\frac{1}{4}\)
Das Integral im Intervall \([0,1]\) liefert:
\(\displaystyle\int^{1}_{0} x^3\,\,\,dx=\big[\frac{1}{4}x^4\big]_{0}^{1}=\frac{1}{4}\)
Insgesammt erhalten wir für die Fläche:
\(\displaystyle\int^{1}_{-1} x^3\,\,\,dx=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}\)
Die Fläche zwischen der Funktion und der \(x\)-Achse beträgt \(\frac{1}{2}\) Flächeneinheiten.
Achtung !
Würde man sein Integral nicht aufteilen und beachten, dass der Graph im Intervall \([-1,0]\) unterhalb der \(x\)-Achse verläuft dann würde man folgendes erhalten:
\(\displaystyle\int^{1}_{-1} x^3\,\,\,dx=0\)
Die Fläche zwischen dem Graphen der Funktion \(f(x)=x^3\) und der \(x\)-Achse im Intervall \([-1,1]\) ist jedoch \(\frac{1}{2}\) Flächeneinheiten groß.
Fläche zwischen zwei Funktionen
Beispiel 4
Wie groß ist die Fläche zwischen den zwei folgenden Funktionen.
\(f(x)=-\)\(\frac{x^2}{12}\)\(+5\)
und
\(g(x)=\)\(\frac{x^2}{6}\)\(+4\)
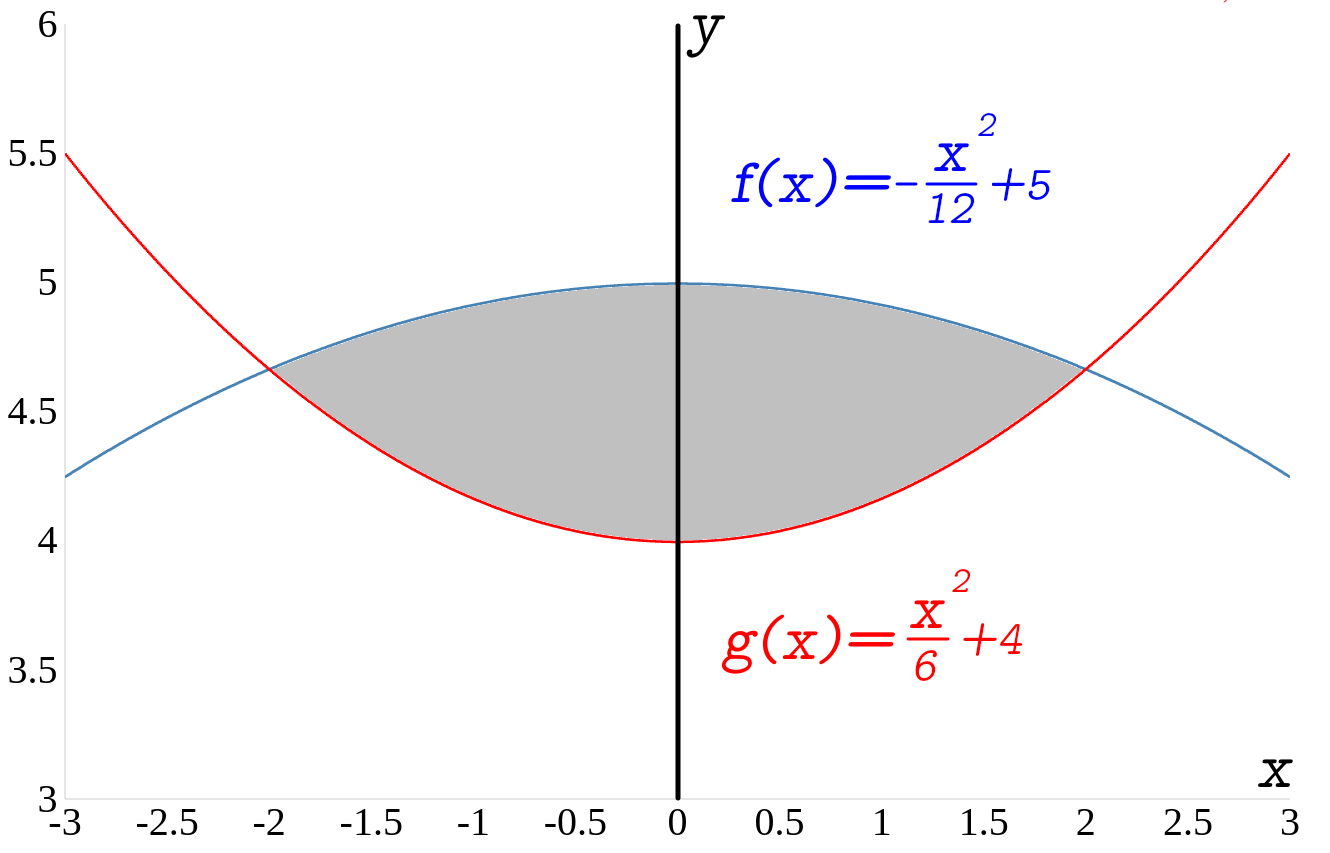
vorgehensweise
- Zunächst müssen die Schnittpunkte \(x_1\) und \(x_2\) der zwei Funktionen Berechnet werden.
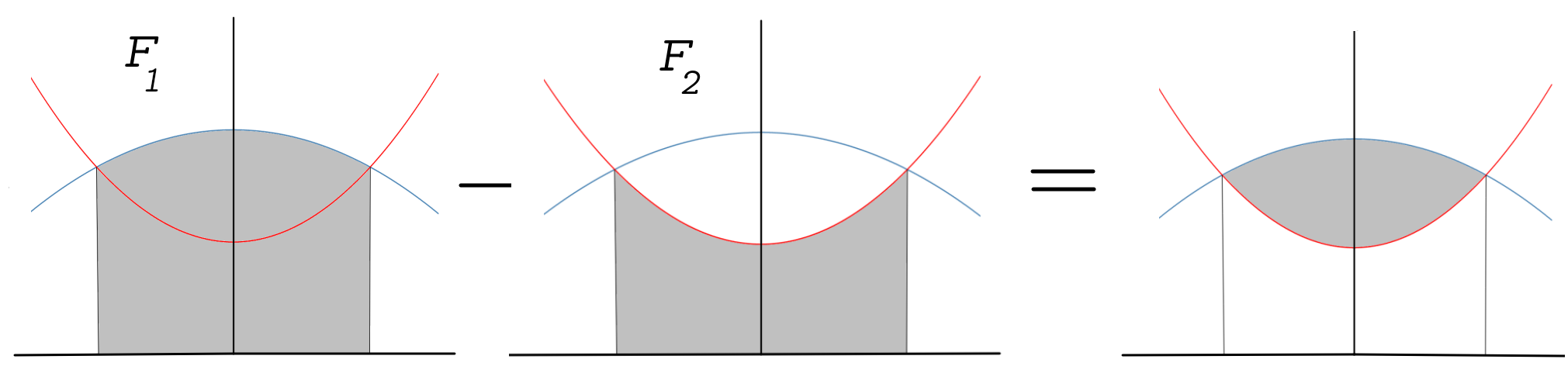
- Anschließend wird die Fläche zwischen der \(x\)-Achse und der Funktion \(f(x)\) im Intervall \([x_1,x_2]\)berechnet. Nennen wir diese Fläche \(F_1\).
- Dann benötigt man noch die Fläche zwischen der Funktion \(g(x)\) und \(x\)-Achse im Intervall \([x_1,x_2]\). Diese Fläche nennen wir \(F_2\).
- Um die Fläche zwischen den zwei Funktionen zu bekommen müssen wir die Flächen \(F_1\) und \(F_2\) von einander abziehen, also \(F_1-F_2\) berechnen.
Wurzelfunktion Integrieren
\(\begin{aligned} f(x)&=\sqrt{x}\\ \\ F(x)&=\frac{2}{3}x^{\frac{3}{2}} \end{aligned}\)
Das Integral der Wurzelfunktion ist sehr leicht zu berechnen, wenn man weis, wie die Wurzelfunktion in eine Potenzfunktion umgeschrieben wird.
Wurzelfunktion in Potenzfunktion umschrieben
\(\sqrt{x}=x^{\frac{1}{2}}\)
\(\sqrt[3]{x}=x^{\frac{1}{3}}\)
\(\sqrt[5]{x}=x^{\frac{1}{5}}\)
...
Hat man eine Wurzelfunktion in die dazugehörige Potenzfunktion umgeschrieben, so kann man ganz einfach die Potenzregel anwenden um die Wurzelfunktion zu integrieren.
\(f(x)=\sqrt{x}=x^{\frac{1}{2}}\)
\(F(x)=\Big(\)\(\frac{1}{\frac{1}{2}+1}\)\(\Big)x^{\frac{1}{2}+1}=\frac{2}{3}x^{\frac{3}{2}}=\frac{2}{3}\sqrt{x^3}\)
Solche Funktionen kannst du mit dem Integralrechner von Simplexy sehr leicht integrieren.
e-Funktion integrieren
Das Integral der \(e\)-Funktion ist sehr leicht zu bestimmen. Denn wir wissen aus der Differentialrechnung das die Ableitung der e-Funktion wieder die e-Funktion ergibt.
\((e^{x})'=e^{x}\)
Da die Integration gerade das Umkehren der Ableitung ist, muss die Stammfunktion der e-Funktion wieder die e-Funktion sein.
Regel:
\(\underbrace{F(x)=e^{x}}_{\text{Stammfunktion}}\overbrace{\leftarrow}^{\text{integrieren}} f(x)=e^{x}\overbrace{\rightarrow}^{\text{ableiten}} \underbrace{f'(x)=e^{x}}_{\text{1.Ableitung}}\)
\(e^{-x}\) Integrieren
Möchte man die Funktion \(e^{-x}\) integrieren, so muss beachtet werden, dass sich im Exponenten zusätzlich zum \(x\) noch ein Minus befindet.
Leiten wir mal zur Probe die Funktion \(f(x)=e^{-x}\) ab:
\(f'(x)=-e^{-x}\)
Das Minus ist aus dem Exponenten nach unten gekommen.
Nun Fragen wir uns, welche Funktion müssen wir ableiten um \(e^{-x}\) zu erhalten?
Die Antwort wäre:
\(F(x)=-e^{-x}\)
Wir können eine Probe machen und die Stammfunktion \(F(x)\) ableiten:
\(F'(x)=-(-e^{-x})'=e^{-x}\)
Die Stammfunktion von \(e^{-x}\) ist somit \(-e^{-x}\).
Berechnet man das Integral einer Funktion, kann man sich die Frage stellen,
"Welche Funktion muss ich ableiten um auf die gegebene Funktion zu kommen?"
Beim Integrieren der \(e\)-Funktion muss darauf geachtet werden ob im Exponenten nur ein \(x\) steht oder nicht. Wenn im Exponenten mehr als nur ein \(x\) steht, so muss man eventuell die Integration mittels Substitution durchführen.
Logarithmus Funktion integrieren
Regel
Integral der Logarithmus-Funktion
\(\displaystyle\int ln(x)\,dx=ln(x)\cdot x-x\)
Das Integral der Logarithmus Funktion ist etwas schwerer. Für die Herleitung kann man Hier Clicken,
Sinus Funktion Integrieren
Die Stammfunktion der Sinus Funktion lautet Minus Cosinus, das kann man sich ziemlich leicht merken.
\(\begin{aligned} f(x)&=sin(x)\\ \\ F(x)&=-cos(x) + C \end{aligned}\)
Man muss jedoch darauf achten, dass im Sinus nur ein \(x\) steht. Wenn dort mehr als \(x\) steht z.B \(sin(2x+1)\), so muss man das Integral über die Substitution berechnen.
Regel
Stammfunktion von Sinus
Die Stammfunktion vom Sinus ergibt die Minus Cosinus Funktion.
Integral von \(f(x)=sin(x)\) ergibt:
\(\displaystyle\int sin(x)\,dx =-cos(x) + C \)
\(F(x)=-cos(x) + C \)
Dabei ist \(C\) eine beliebige Konstante.
Cosinus Funktion Integrieren
Die Stammfunktion vom Cosinus ist der Sinus.
\(\begin{aligned} f(x)&=cos(x)\\ \\ F(x)&=sin(x) + C \end{aligned}\)
Auch hier muss man darauf achten, ob im Argument vom Cosinus mehr als nur \(x\) steht z.B \(cos(2x+1)\). In dem Fall müsste man das Integral über die Substitution berechnen.
Regel
Stammfunktion von Cosinus
Die Stammfunktion vom Cosinus ergibt die Sinus Funktion.
Integral von \(f(x)=cos(x)\) ergibt:
\(\displaystyle\int cos(x) dx =sin(x) + C \)
\(F(x)=sin(x) + C \)
Dabei ist \(C\) eine beliebige Konstante.
