Obersumme und Untersumme

Der Integralrechner von Simplexy kann beliebige Funktionen für dich integrieren und noch viel mehr. Berechne ganz simple die Stammfunktion und die Flächen unter einem Graphen.

Die Fläche unter einem Graphen kann näherungsweise mit der Obersumme bzw. der Untersumme ermittelt werden. Ein bestimmtes Integral ist schlussendlich nix anderes als ein Grenzwert der Obersumme bzw. der Untersumme. Welche verfahren gibt es, um die Fläche unter einer Funktion näherungsweise zu bestimmten ?

Die Streifenmethode des Archimedes ist ein Verfahren, um die Fläche zwischen einer Funktion und der \(x\)-Achse näherungsweise zu ermitteln.

In der unteren Abbildung siehst du die Funktion \(f(x)=x^2\) und das Flächenstück \(F\), welches von dem Funktionsgraphen der Funktion im Intervall \([1,2]\) und der \(x\)-Achse eingeschlossen wird.

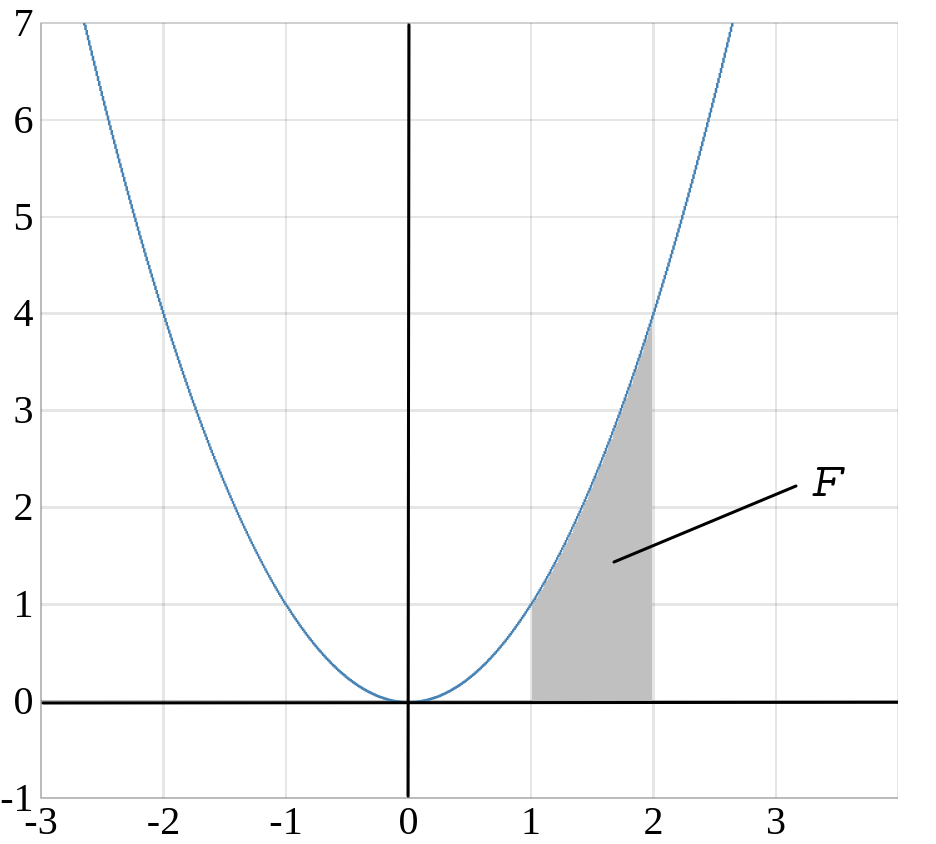
Das Flächenstück \(F\) kann durch feine Rechtecke näherungsweise überdeckt werden.

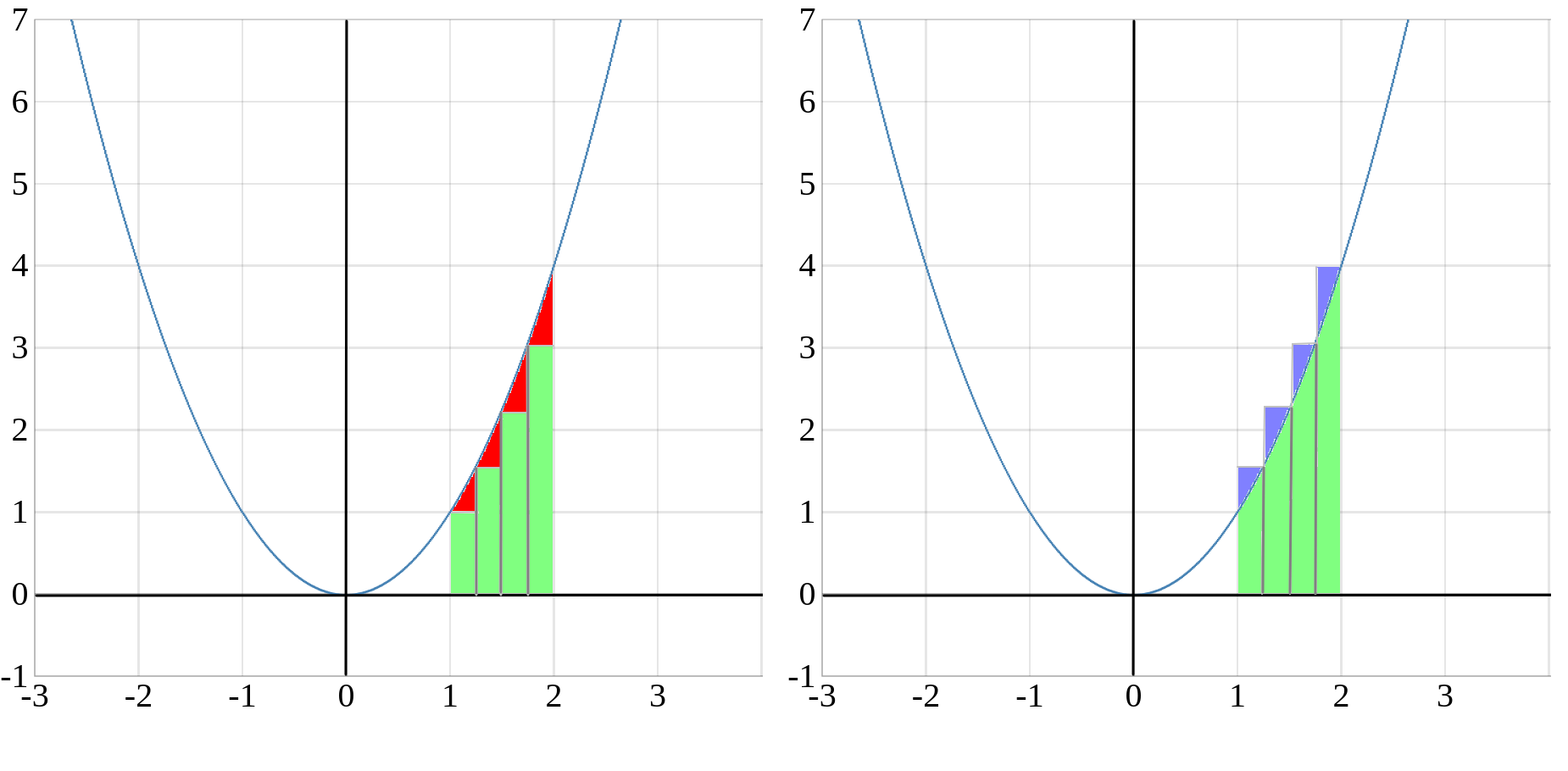
Indem Archimedes die Fläche unter der Funktion in kleine Rechtecke zerlegte, näherte er die tatsächliche Fläche durch zwei berechenbare Flächen an.

Links sind vier Rechtecke, die alle komplett unterhalb des Funktionsgraphen liegen. Die Summe der entsprechenden Flächeninhalten nennt man Untersumme. Die Untersumme ist stets etwas kleiner als die tatsächliche Fläche zwischen dem Funktionsgraphen und der \(x\)-Achse.

Rechts liegen die Flächenstücke zumteil oberhalb des Funktionsgraphen. Die Summe der entsprechenden Flächeninhalten nennt man Obersumme, man erhält mit der Obersumme einen Wert der stets etwas größer ist als die tatsächliche Fläche zwischen Funktionsgraphen und \(x\)-Achse.

Im Folgenden wird die Obersumme und die Untersumme für das Intervall \([1,2]\) im bezug auf die quadratische Funktion \(f(x)=x^2\) berechnet.

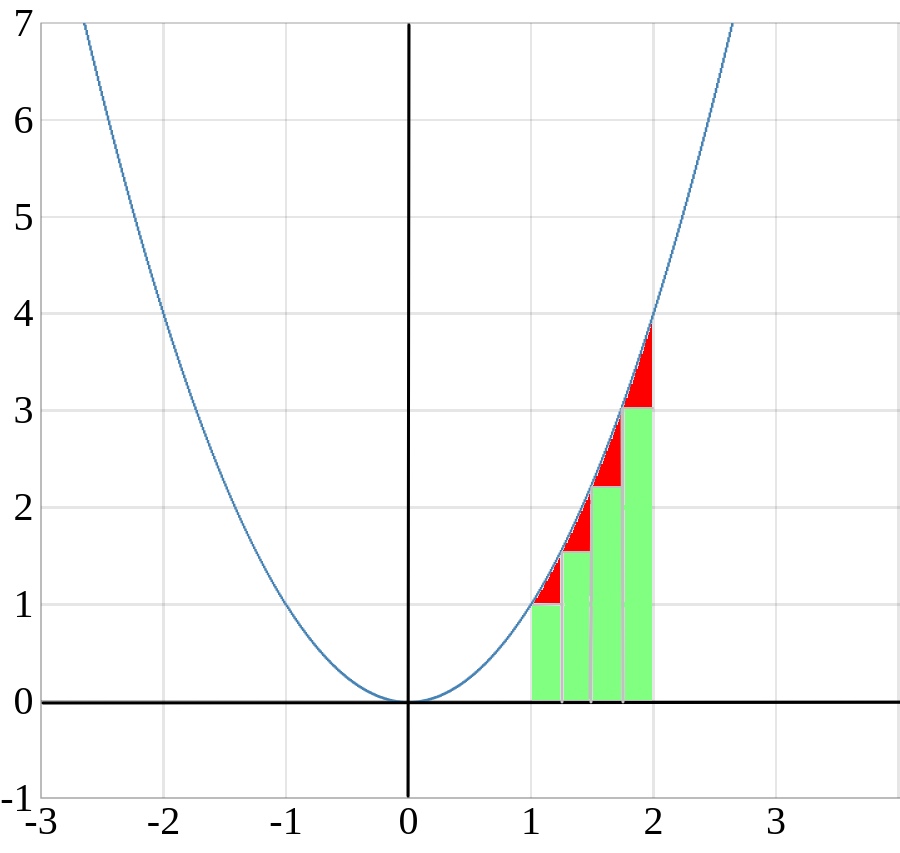
Zunächst haben wir das Intervall \([1,2]\) indem wir die Fläche unter dem Graphen berechnen wollen in vier Teilintervalle unterteilt, mit je einer Breite von \(\frac{1}{4}\). Aus jedem Teilintervall konstruieren wir ein Rechteck, dessen Höhe gerade der kleinste Funktionswert auf dem entsprechenden Teilintervall ist. Die Summe aus den Flächeninhalten \(U\) der Teilintervalle berechnet sich über:

\(U=\frac{1}{4}\big(f(1)+f(1,25)+f(1,5)+f(1,75)\big)\)

\(\,\,\,\,\,\,\,=\frac{1}{4}\big(1^2+1,25^2+1,5^2+1,75^2\big)\)

\(\,\,\,\,\,\,\,=1,96875\)

Die Berechnung der Obersumme erfolgt genau wie die Berechnung der Untersumme, einziger unterschied besteht in der Höhe der Teilrechtecke. Man nimmt bei der Obersumme als Höhe, den größten Funktionswert im entsprechenden Teilintervall.

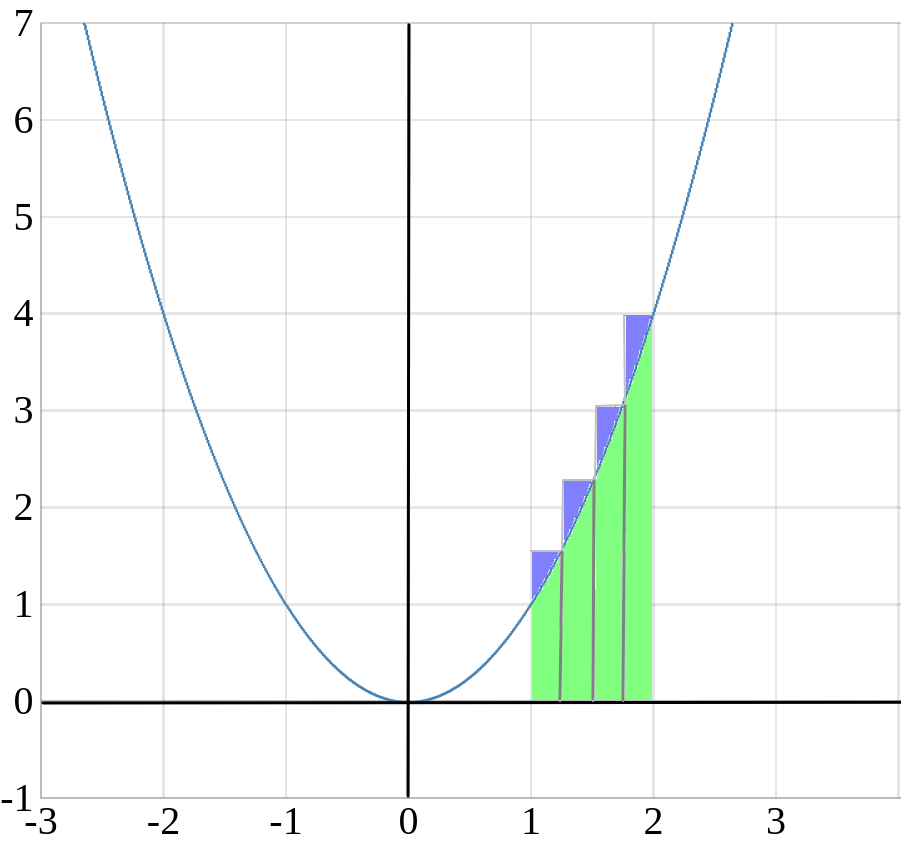
Die Obersumme berechnet sich über:

\(O=\frac{1}{4}\big(f(1,25)+f(1,5)+f(1,75)+f(2)\big)\)

\(\,\,\,\,\,\,\,=\frac{1}{4}\big(1,25^2+1,5^2+1,75^2+2^2\big)\)

\(\,\,\,\,\,\,\,=2,71875\)