Stammfunktion
Stammfunktion Rechner
Der Stammfunktion Rechner von Simplexy kann dir die Stammfunktion berechnen und noch viel mehr. Nutze den Integralrechner um das bestimmte und unbestimmte Integal von Funktionen zu ermitteln.
Stammfunktion
Beim Integrieren (Aufleiten) einer Funktion ist die Stammfunktion gesucht. In anderen Worten, dass unbestimmte Integral einer Funktion ist die Stammfunktion. Wie man in dem Beitrag zur Integralrechnung lesen kann, ist das Integrieren (Aufleiten) die umgekehrte Operation zum Ableiten.
Das Integrieren ist die Umkehrung der Ableitung
\(\underbrace{F(x)}_{\text{Stammfunktion}}\overbrace{\longleftarrow}^{\text{integrieren}} f(x)\overbrace{\longrightarrow}^{\text{ableiten}} \underbrace{f'(x)}_{\text{1.Ableitung}}\)
\(\underbrace{F(x)}_{\text{Stammfunktion}}\overbrace{\longrightarrow}^{\text{ableiten}} f(x)\overbrace{\longleftarrow}^{\text{integrieren}} \underbrace{f'(x)}_{\text{1.Ableitung}}\)
Stammfunktion einfach erklärt
Um das Integral einer Funktion berechnen zu können, muss man die Stammfunktion berechnen.
Wenn \(f(x)\) eine reelle Funktion ist, dann erfüllt die Stammfunktion \(F(x)\) folgende Bedingung.
\(\begin{aligned} F'(x)=f(x) \end{aligned}\)
Die Ableitung der Stammfunktion \(F(x)\) ergibt die Funktion \(f(x)\).
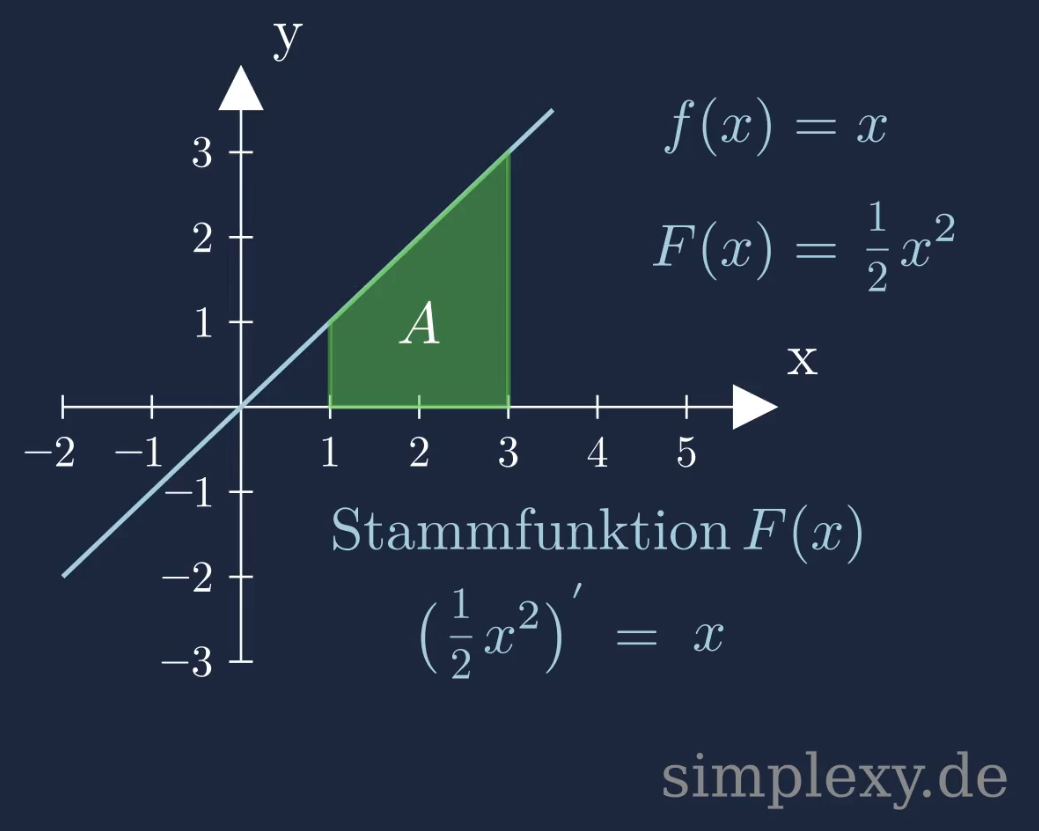
Jede stetige Funktion \(f(x)\) besitzt eine Stammfunktion \(F(x)\). Man muss also nur noch wissen wie man die Stammfunktion berechnen kann.
Merke
Man verwendet für die Stammfunktion meistens Großbuchstaben.
\(F(x)\) ist die Stammfunktion von \(f(x)\).
\(G(x)\) ist die Stammfunktion von \(g(x)\).
usw...
Stammfunktion berechnen
In diesem Abschnitt wirst du sehen wie man eine Stammfunktion berechnen kann. Doch bevor wir dazu kommen, wird die allgemeine Schreibweise eingeführt.
Allgemeine Schreibenweise
Die Stammfunktion wird im Allgemeinen wie folgt dargestellt:
\(\displaystyle\int f(x)\,\,dx=F(x)+c\)
Achtung
Die Konstante \(c\) ist wichtig, da jede Funktion \(f(x)\) unendlich viele Stammfunktionen besitzt. Alle Stammfunktionen einer Funktion unterscheiden sich lediglich um eine Konstante \(c\), die addiert oder subtrahiert wird. Beim Ableiten der Stammfunktion, fällt die Konstante \(c\) weg.
Stammfunktion bilden
Dir ist die Funktion \(f(x)\) gegeben und du sollte die Stammfunktion \(F(x)\) berechnen. Du weißt bereits, dass die Ableitung der Stammfunktion zur Ursprungsfunktion \(f(x)\) führt.
\(F'(x)=f(x)\)
Die Stammfunktion \(F(x)\) ist aber noch garnicht bekannt. Diese kann jedoch über das Integral berechnet werden.
\(F(x)=\displaystyle\int f(x)\,\,dx\)
Um das Integral von \(f(x)\) zu berechnen gibt es verschiedene Integrationsregeln die man anwenden kann.
Beim Integrieren geht es im wesentlichen darum heraus zu finden, wie die Stammfunktion \(F(x)\) aussehen muss, sodass man beim Ableiten der Stammfunktion \(F'(x)\) die Ursprungsfunktion \(f(x)\) erhält.
Stammfunktion von Potenzfunktionen
In der folgenden Tabelle sind einige typische Potenzfunktionen und ihre Stammfunktionen eingetragen.
| f(x) | F(x) |
| \(1\) | \(x\) |
| \(4\) | \(4\cdot x\) |
| \(x\) | \(\frac{1}{2}\)\(x^2\) |
| \(x^2\) | \(\frac{1}{3}\)\(x^3\) |
| \(2\cdot x^5\) | \(\frac{2}{6}\)\(x^6\) |
| \(x^2-4\) | \(\frac{1}{3}\)\(x^3-4\cdot x\) |
Dir fällt sicherlich auf, dass man die Stammfunktion einer Potenzfunktion berechnen kann, indem man den Exponenten um \(1\) erhöht und in den Nenner schreibt.
Regel
Stammfunktion von Potenzfunktionen
Die Stammfunktion zu der Potenzfunktion
\(f(x)=x^n\)\(\,\,\,\,\,\,\,\,n\in\natnums\)
berechnet sich über:
\(F(x)=\)\(\frac{1}{n+1}\)\(x^{n+1}\)

Beispiel Stammfunktion berechnen
Berechne die Stammfunktion von
\(f(x)=x^2+2x-1\)
Wir wenden die Regel zur Integration von Potenzfunktionen an und erhalten:
\(\begin{aligned} F(x)&=\frac{1}{3}x^3+\frac{2}{2}x^2-x\\ \\ &=\frac{1}{3}x^3+x^2-x \end{aligned}\)
Um zu überprüfen ob wir richtig integriert haben, können wir die Stammfunktion ableiten und sollten dann auf die Ursprungsfunktion kommen. Das liegt daran, weil das Ableiten die Umkehrung der Integration ist.
\(\begin{aligned} F'(x)&=\Big(\frac{1}{3}x^3+x^2-x\Big)'\\ \\ &=\frac{3}{3}x^2+2x-1\\ \\ &=x^2+2x-1=f(x) \end{aligned}\)
Wie du siehst haben wir die Stamfunktion korrekt ermittelt.
Bemerkung
Wir hätten zu unserer Stammfunktion eine beliebige Konstante addieren können ohne dabei eine falsche Stammfunktion zu erhalten.
\(\begin{aligned} F(x)&=\frac{1}{3}x^3+x^2-x+\underbrace{10}_\text{Konstante} \end{aligned}\)
Denn die Ableitung von \(F(x)\) mit der Konstanten würde immer noch zu unserer Ausgangsfunktion führen. Das liegt daran, dass die Konstante beim ableiten wegfällt.
Denn
\(10'=0\)
Allgemein schreibt man die Konstante in der Stammfunktion folgendermaßen:
\(\begin{aligned} F(x)=\frac{1}{3}x^3+x^2-x+C \end{aligned}\)
Der einfachheithalber lässt man die Konstante oft weg bzw. man setzt.
\(C=0\)
Stammfunktion Bruch
Stammfunktion von Brüchen berechnen, geht in der gleichen Weise wie bei Potenzfunktionen. Ein Bruch lässt sich nämlich in eine Potenzfunktion umschrieben.
Bruch umschreiben
Einige Brüche können in eine Potenzfunktion umgeschrieben werden.
\(\begin{aligned} \frac{1}{x}&=x^{-1}\\ \\ \frac{1}{x^2}&=x^{-2}\\ \\ \frac{1}{x^3}&=x^{-3}\\ \end{aligned}\)
Dabei handelt es sich lediglich um eine neue Schreibweise für den Bruch. Diese neue Schreibweise kann man genau so verinnerlichen wie die Schreibweise:
\(\begin{aligned} x\cdot x=x^2 \end{aligned}\)
Es handelt sich dabei nur um eine mathematische Notation die oftmals das Rechnen erleichtert. Das Umschreiben eines Bruchs in eine Potenzfunktion ermöglicht die Berechnung der Stammfunktion.
Beispiele Stammfunktion Bruch
Beispiel 1
\(\begin{aligned} \displaystyle\int \frac{1}{x^3}\,\,dx&=\displaystyle\int x^{-3}\,\,dx\\ \\ &=-\frac{1}{2}x^{-2}+c=-\frac{1}{2x^2}+c \end{aligned}\)
Beispiel 2
\(\begin{aligned} \displaystyle\int \frac{5}{x^4}\,\,dx&=5\displaystyle\int \frac{1}{x^4}\,\,dx=5\displaystyle\int x^{-4}\,\,dx\\ \\ &=5\frac{1}{-3}x^{-3}+c=-\frac{5}{3x^3}+c \end{aligned}\)
Mit dem Stammfunktion Rechner kannst du ganz einfach die Stammfunktion berechnen.
Stammfunktion 1/x
Um die Stammfunktion von 1/x berechnen zu können, muss man beachtet, dass die Potenzregel hier nicht klappt.
\(\frac{1}{x}=x^{-1}\)
Wenn du hier die Potenzregeln anwendest um die Stammfunktion zu berechnen, so wirst du sehen, dass im Exponenten eine Null stehen wird. Man kommt mit der klassischen Regel hier nicht weiter, dafür gibt es jedoch eine andere Regel.
1/x Stammfunktion
\(\displaystyle\int \frac{1}{x}=ln(|x|)+c\)
Dies ist eine Folge der logarithmischen Integrationsregel, welche folgendes besagt:
logarithmische Integrationsregel
\(\displaystyle\int \frac{f'(x)}{f(x)}\,\,dx=ln(|f(x)|)+c\)
Ist \(f(x)=x\) so ist \(f'(x)=1\) und das Integral lautet:
\(\displaystyle\int \frac{f'(x)}{f(x)}\,\,dx=\displaystyle\int \frac{1}{x}\,\,dx=ln(|x|)+c\)
Stammfunktion e-Funktion
Die Stammfunktion der \(e\)-Funktion ist wieder die \(e\)-Funktion.
Regel:
\(\underbrace{F(x)=e^{x}}_{\text{Stammfunktion}}\overbrace{\leftarrow}^{\text{integrieren}} f(x)=e^{x}\overbrace{\rightarrow}^{\text{ableiten}} \underbrace{f'(x)=e^{x}}_{\text{1.Ableitung}}\)
\(e^{-x}\) Integrieren
Möchte man die Stammfunktion von \(e^{-x}\) berechnen, so muss beachtet werden, dass sich im Exponenten zusätzlich zum \(x\) noch ein Minus befindet.
Leiten wir mal zur Probe die Funktion \(f(x)=e^{-x}\) ab:
\(f'(x)=-e^{-x}\)
Das Minus ist aus dem Exponenten nach unten gekommen.
Nun Fragen wir uns, welche Funktion müssen wir ableiten um \(e^{-x}\) zu erhalten?
Die Antwort wäre:
\(F(x)=-e^{-x}\)
Wir können eine Probe machen und die Stammfunktion \(F(x)\) ableiten:
\(F'(x)=-(-e^{-x})=e^{-x}\)
Die Stammfunktion von \(e^{-x}\) ist somit \(-e^{-x}\).
Bei der Stammfunktion der \(e\)-Funktion muss darauf geachtet werden ob im Exponenten nur ein \(x\) steht oder nicht. Wenn im Exponenten mehr als nur ein \(x\) steht, so muss man eventuell die Integration mittels Substitution durchführen.
\(\begin{aligned} f(x)&=e^{-x}\\ \\ F(x)&=-e^{-x} \end{aligned}\)
Stammfunktion Wurzel x
Ähnlich wie bei der Stammfunktion von Brüchen, kann man die Stammfunktion von Wurzelfunktionen über die Potenzregel berechnen. Dazu muss man die folgende Umschreibung anwenden:
\(\sqrt{x}=x^{\frac{1}{2}}\)
Damit gilt für die Stammfunktion von wurzel x:
\(\begin{aligned} \displaystyle\int \sqrt{x}\,\,dx = \displaystyle\int x^{\frac{1}{2}}\,\,dx=\frac{2}{3}x^{\frac{3}{2}}=\frac{2}{3}\sqrt{x^3} \end{aligned}\)
Stammfunktion wurzel x
\(\begin{aligned} f(x)&=\sqrt{x}\\ \\ F(x)&=\frac{2}{3}\sqrt{x^3} \end{aligned}\)
Stammfunktion ln(x)
Die Stammfunktion der Logarithmus Funktion kann mittels partieller Integration berechnet werden.
Regel
Integral der Logarithmus-Funktion
\(\displaystyle\int ln(x)\,dx=ln(x)\cdot x-x\)
Das Integral der Logarithmus Funktion ist etwas schwerer. Für die Herleitung kann man Hier Clicken,
Stammfunktion sin(x)
Die Stammfunktion der Sinus Funktion lautet wie folgt:
\(\begin{aligned} f(x)&=sin(x)\\ \\ F(x)&=-cos(x) + C \end{aligned}\)
Regel
Stammfunktion von Sinus
Die Stammfunktion vom Sinus ergibt die Minus Cosinus Funktion.
Integral von \(f(x)=sin(x)\) ergibt:
\(\displaystyle\int sin(x)\,dx =-cos(x) + C \)
\(F(x)=-cos(x) + C \)
Dabei ist \(C\) eine beliebige Konstante.
Stammfunktion cos(x)
Die Stammfunktion vom Cosinus ist der Sinus.
\(\begin{aligned} f(x)&=cos(x)\\ \\ F(x)&=sin(x) + C \end{aligned}\)
Regel
Stammfunktion von Cosinus
Die Stammfunktion vom Cosinus ergibt die Sinus Funktion.
Integral von \(f(x)=cos(x)\) ergibt:
\(\displaystyle\int cos(x) dx =sin(x) + C \)
\(F(x)=sin(x) + C \)
Dabei ist \(C\) eine beliebige Konstante.
Stammfunktion Tabelle
| f(x) | F(x) |
| \(e^x\) | \(e^x\) |
| \(3e^{3x}+1\) | \(e^{3x}+x\) |
| \(e^{2x}\) | \(\frac{1}{2}\)\(e^{2x}\) |
| \(e^{-2x}\) | \(-\frac{1}{2}\)\(e^{-2x}\) |
| \(\frac{1}{x}\) | \(ln(x)\) |
| \(\frac{1}{x^2}\) | \(-\frac{1}{x}\) |
| \(sin(x)\) | \(-cos(x)\) |
| \(cos(x)\) | \(sin(x)\) |
