Determinante berechnen
Determinanten Rechner
Der Determinanten Rechner von Simplexy kann beliebige Matrix Rechenoperationen für dich durchführen. Mit dem Rechner kannst du die Determinante einer Matrix berechnen und viel mehr.
Determinante berechnen
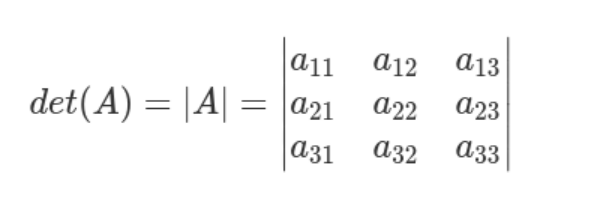
In diesem Beitrag wirst du lernen wie man eine Determinante berechnen kann und was die Eigenschaften der Determinante sind. Doch bevor wir zu der Berechnung einer Determinante kommen, fragen wir uns was die Determinante ist?
Determinante Definition
Die Determinante einer quadratischen Matrix ist eine Zahl die ihr zugeordnet wird und aus ihren Einträgen berechnet wird. Über die Determinante werden Eigenschaften einer Matrix ermittelt. So ist beispielsweise eine Matrix genau dann invertierbar, wenn die Determinante dieser Matrix ungleich null ist. Im folgenden werden wir noch weitere Eigenschaften der Determinante besprechen.
Beispiel
\(A=\begin{pmatrix}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \\\end{pmatrix}\)
Die Determinante der Matrix A lautet:
\(det(A)=|A|=\begin{vmatrix}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \\\end{vmatrix}\)
Wie berechnet man die Determinante einer Matrix ?
Für die Berechnung der Determinante gibt es den Laplace'schen Entwicklungssatz und den Gauß-Algorithmus.
Für 2x2 Matrizen und 3x3 Matrizen gibt es eine einfache Formel um die Determinante zu berechnen.
2x2 Matrix Determinante berechnen
Wie berechnet man die Derminante einer 2x2 Matrix ?
Beispiel
\(A=\begin{pmatrix}\textcolor{red}{a} & \textcolor{green}{b} \\\textcolor{green}{c} & \textcolor{red}{d}\\\end{pmatrix}\)
\(det(A)=|A|=\begin{vmatrix}\textcolor{red}{a} & \textcolor{green}{b} \\\textcolor{green}{c} & \textcolor{red}{d}\\\end{vmatrix}\)
Man benötigt für die Berechnung der Determinante einer 2x2 Matrix das Produkt der Elemente der Hauptdiagonale.
\(\textcolor{red}{a}\cdot \textcolor{red}{d}\)
Ebenfalls benötigt man das Produkt der Elemente der Nebendiagonale.
\(\textcolor{green}{c}\cdot \textcolor{green}{b}\)
Die Formel zur Berechnung der Determinante einer 2x2 Matrix lautet:
\(|A|=\begin{vmatrix}\textcolor{red}{a} & \textcolor{green}{b} \\\textcolor{green}{c} & \textcolor{red}{d}\\\end{vmatrix}=\textcolor{red}{a}\cdot \textcolor{red}{d}-\textcolor{green}{c}\cdot \textcolor{green}{b}\)
Konkrete Beispiele
\(|A|=\begin{vmatrix}2 & 2 \\2 & 2\\\end{vmatrix}=2\cdot 2-2\cdot 2=0\)
\(|B|=\begin{vmatrix}1 & 2 \\3 & 4\\\end{vmatrix}=1\cdot 4-3\cdot 2=-2\)
\(|C|=\begin{vmatrix}2 & 5 \\1 & 3\\\end{vmatrix}=2\cdot 3-1\cdot 5=1\)
3x3 Matrix Determinante berechnen
Wie berechnet man die Derminante einer 3x3 Matrix ?
Beispiel
\(A=\begin{pmatrix}a & b & c\\d & e & f \\ g & h & i \\\end{pmatrix}\)
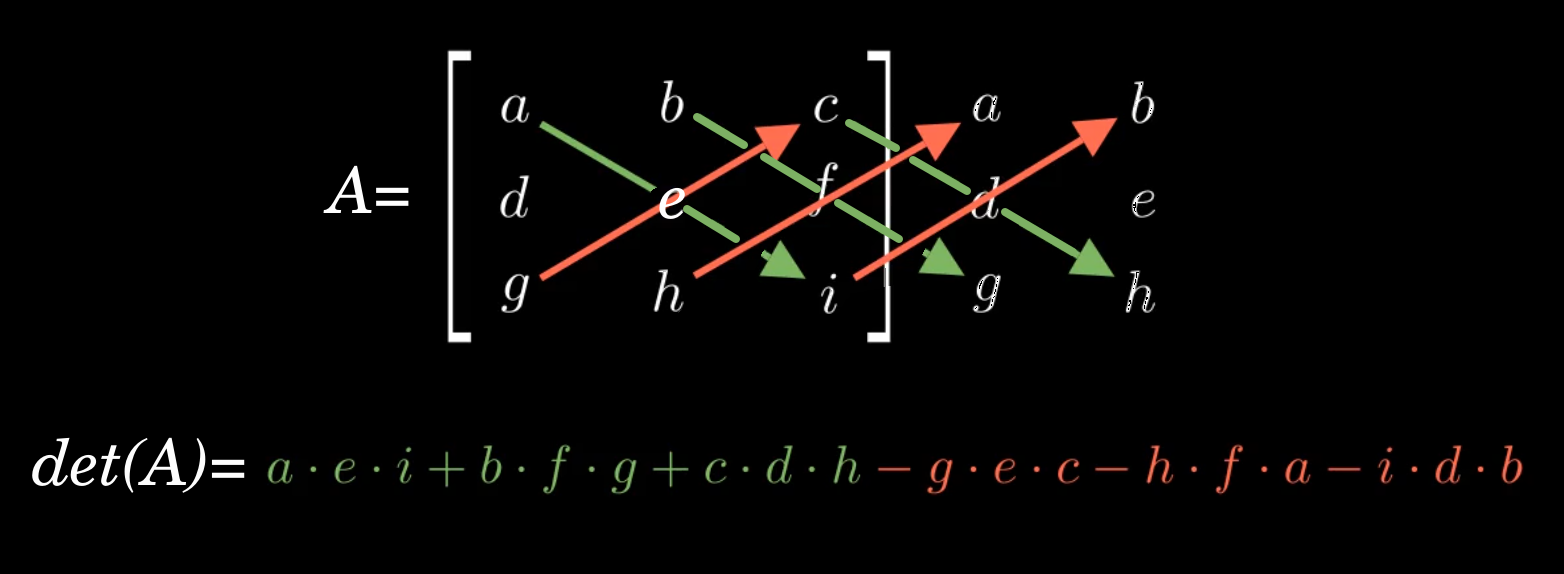
Mit der Regel von Sarrus lässt sich die Derminante einer 3x3 Matrix berechnen. Dazu schreibt man die ersten zwei Spalten rechts neben der Ausgangsmatrix und bildet das Produkt der drei Diagonalen.
\(|A|=\begin{vmatrix}a & b & c\\d & e & f \\ g & h & i \\\end{vmatrix}\begin{matrix}a & b \\d & e \\ g & h \\\end{matrix}\)
Das Produkt aus den drei Diagonalen, die von oben links nach unten rechts verlaufen lautet.
\(a\cdot e\cdot i+b\cdot f\cdot g+c\cdot d\cdot h\)
Ebenso berechnet man das Produkt aus den drei Diagonale, die von unten links nach oben rechts verlaufen.
\(-g\cdot e\cdot c -h\cdot f\cdot a-i\cdot d\cdot b\)
Anschließend muss man nur noch diese zwei Produkte aus den Diagonalen von einander abziehen.
\(|A|=\begin{vmatrix}a & b & c\\d & e & f \\ g & h & i \\\end{vmatrix}=\)
\(a\cdot e\cdot i+b\cdot f\cdot g+c\cdot d\cdot h-g\cdot e\cdot c -h\cdot f\cdot a-i\cdot d\cdot b\)
Konkretes Beispiel
\(A=\begin{pmatrix}1 & 2 & 3\\4 & 5 & 6 \\ 7 & 8 & 9 \\\end{pmatrix}\)
\(|A|=\begin{vmatrix}1 & 2 & 3\\4 & 5 & 6 \\ 7 & 8 & 9 \\\end{vmatrix}\)
\(=1\cdot 5\cdot 9+2\cdot 6\cdot 7+3\cdot 4\cdot 8-7\cdot 5\cdot 3-8\cdot 6\cdot 1-9\cdot 4\cdot 2\)
\(=45+84+96-105-48-72=0\)
Determinante Eigenschaften
Transponierte Determinante
Die Determinante einer Matrix ist genau so groß wie die Determinante ihrer Transponierten:
\(|A|=|A|^T\)
Zeilen und Spalten vertauschen
Vertauscht man die Zeilen oder die Spalten einer Determinante, eine ungerade Anzahl an malen, so ändert sich das Vorzeichen der Determinante.
\(|A|=\begin{vmatrix}\textcolor{red}{a} & \textcolor{red}{b} & \textcolor{red}{c}\\d & e & f \\ g & h & i \\\end{vmatrix}=-\begin{vmatrix}d & e & f\\\textcolor{red}{a} & \textcolor{red}{b} & \textcolor{red}{c} \\ g & h & i \\\end{vmatrix}\)
Vertauscht man die Zeilen oder die Spalten einer Determinante, eine gerade Anzahl an malen, so ändert sich das Vorzeichen der Determinante nicht.
\(|A|=\begin{vmatrix}\textcolor{red}{a} & \textcolor{red}{b} & \textcolor{red}{c}\\d & e & f \\ g & h & i \\\end{vmatrix}=\begin{vmatrix} d & e & f\\g & h & i \\\textcolor{red}{a} & \textcolor{red}{b} & \textcolor{red}{c}\\\end{vmatrix}\)
Multiplikation mit einer Zahl
Wird eine Zeile oder eine Spalte der Matrix mit einer Zahl multipliziert, so multipliziert sich auch die Determinante der Matrix mit der Zahl:
\(det(B)=|B|=\begin{vmatrix}a & b & c\\d & e & f \\ g & h & i \\\end{vmatrix}\)
\(\begin{vmatrix}\textcolor{red}{\lambda}\cdot a &\textcolor{red}{\lambda}\cdot b &\textcolor{red}{\lambda}\cdot c\\d & e & f \\ g & h & i \\\end{vmatrix}=\textcolor{red}{\lambda}\cdot det(B)\)
\(\begin{vmatrix}\textcolor{red}{\lambda}\cdot a &b &c\\\textcolor{red}{\lambda}\cdot d & e & f \\\textcolor{red}{\lambda}\cdot g & h & i \\\end{vmatrix}=\textcolor{red}{\lambda}\cdot det(B)\)
Produkt aus Matrizen
Die Determinante aus dem Produkt von zwei Matrizen ist dem Produkt ihrer Determinanten gleich:
\(|A\cdot B|=|A|\cdot |B|\)
Det(A)=0
Die Determinante einer Matrix ist gleich null wenn eines der folgenden Fälle auf die Matrix zutrifft:
Eine oder mehr Spalten/Zeilen nur aus Nullen bestehen.
Zwei oder mehr Spalten/Zeilen gleich sind.
Eine Spalte/Zeile aus einer Linearkombination anderer Spalten oder Zeilen besteht.
Determinante berechnen nxn
Wir gucken uns nun noch an, wie man die Determinante einer großen Matrix berechnen kann. Für große Matrizen muss man den Laplace Entwicklungssatz verwenden um die Determinante berechnen zu können.
Laplace Entwicklungssatz
Ist eine nxn Matrix \(A\) gegeben
\(\begin{aligned} \begin{pmatrix}a_{11} & a_{12} & ... & a_{1n}\\ a_{21} & a_{22} & ... &a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn} \\\end{pmatrix} \end{aligned}\)
dann kann man die Determinante berechnen, indem man den Laplaceschen Entwicklungssatz verwendet.
Entwicklung nach der i-ten Zeile
\(\begin{aligned} det(A)=\sum_{j=1}^{n}a_{ij}\cdot (-1)^{i+j}\cdot det(A_{ij}) \end{aligned}\)
Entwicklung nach der j-ten Spalte
\(\begin{aligned} det(A)=\sum_{i=1}^{n}a_{ij}\cdot (-1)^{i+j}\cdot det(A_{ij}) \end{aligned}\)
Dabei ist \(a_{ij}\) der Eintrag der Matrix \(A\) in der i-ten Zeile und j-ten Spalte. \(A_{ij}\) die Matrix A, wobei die i-te Zeile und die j-te Spalte von \(A\) gestrichen ist. Um den Laplaceschen Entwicklungssatz anwenden zu können rechnen wir als Beispiel die Determinante einer 4x4 Matrix vor.
Determinante berechnen 4x4 Matrix
Gegeben ist die folgende 4x4 Matrix
\(\begin{aligned} A=\begin{pmatrix} 3 & 7 & 3 & 0\\ 0 & 2 & -1 & 1\\ 5 & 4 & 3 & 2\\ 6 & 6 & 4 & -1 \\\end{pmatrix} \end{aligned}\)
Berechne die Determinante der 4x4 Matrix \(A\) aus.
Lösung
\(\begin{aligned} det(A)=\begin{vmatrix}3 & 7 & 3 & 0\\ 0 & 2 & -1 & 1\\ 5 & 4 & 3 & 2\\ 6 & 6 & 4 & -1 \\\end{vmatrix} \end{aligned}\)
Die Entwicklung findet nach der ersten Spalte statt.
\(\begin{aligned} det(A)=& 3\cdot \underbrace{\begin{vmatrix} 2& -1 & 1\\ 4 & 3 & 2\\ 6 & 4 & -1\\\end{vmatrix}}_{-40} - 0 \cdot \underbrace{\begin{vmatrix} 7& 3 & 0\\ 4 & 3 & 2\\ 6 & 4 & -1\\\end{vmatrix}}_{-29} \\ \\ \\ \\ & + 5\cdot \underbrace{\begin{vmatrix} 7& 3 & 0\\ 2 & -1 & 1\\ 6 & 4 & -1\\\end{vmatrix}}_{3} - 6 \cdot \underbrace{\begin{vmatrix} 7& 3 & 0\\ 2 & -1 & 1\\ 4 & 3 & 2\\\end{vmatrix}}_{-35} \end{aligned}\)
Wobei die Determinanten der 3x3 Matrizen mit der Regel von Sarrus leicht zu berechnen sind.
\(\begin{aligned} det(A)=3\cdot (-40) - 0\cdot (-29) +5 \cdot 3 - 6\cdot (-35)=105 \end{aligned}\)
Damit haben wir also die Determinante der 4x4 Matrix A berechnet. Es gilt \(det(A)=105\).
