Matrizen Multiplizieren
Matrizen Rechner
Der Matrizen Rechner von Simplexy kann beliebige Matrix Rechenoperationen für dich durchführen. Mit dem Rechner kannst du Matrizen multiplizieren und viel mehr. Probiere den Rechner jetzt aus.
Matrizenmultiplikation
In diesem Beitrag werden wir uns mit der Matrizenmultiplikation beschäftigen.
Die Multiplikation von Matrizen ist sehr einfach, wenn man das Schema der Matrizenmultiplikation anwendet. In diesem Beitrag wirst du die Matrix Multiplikation einfach erklärt bekommen. Des Weiteren ist in dem oberen Video das Schema zur Matrizenmultiplikation bereits gezeigt.
Matrizenmultiplikation Bedingung
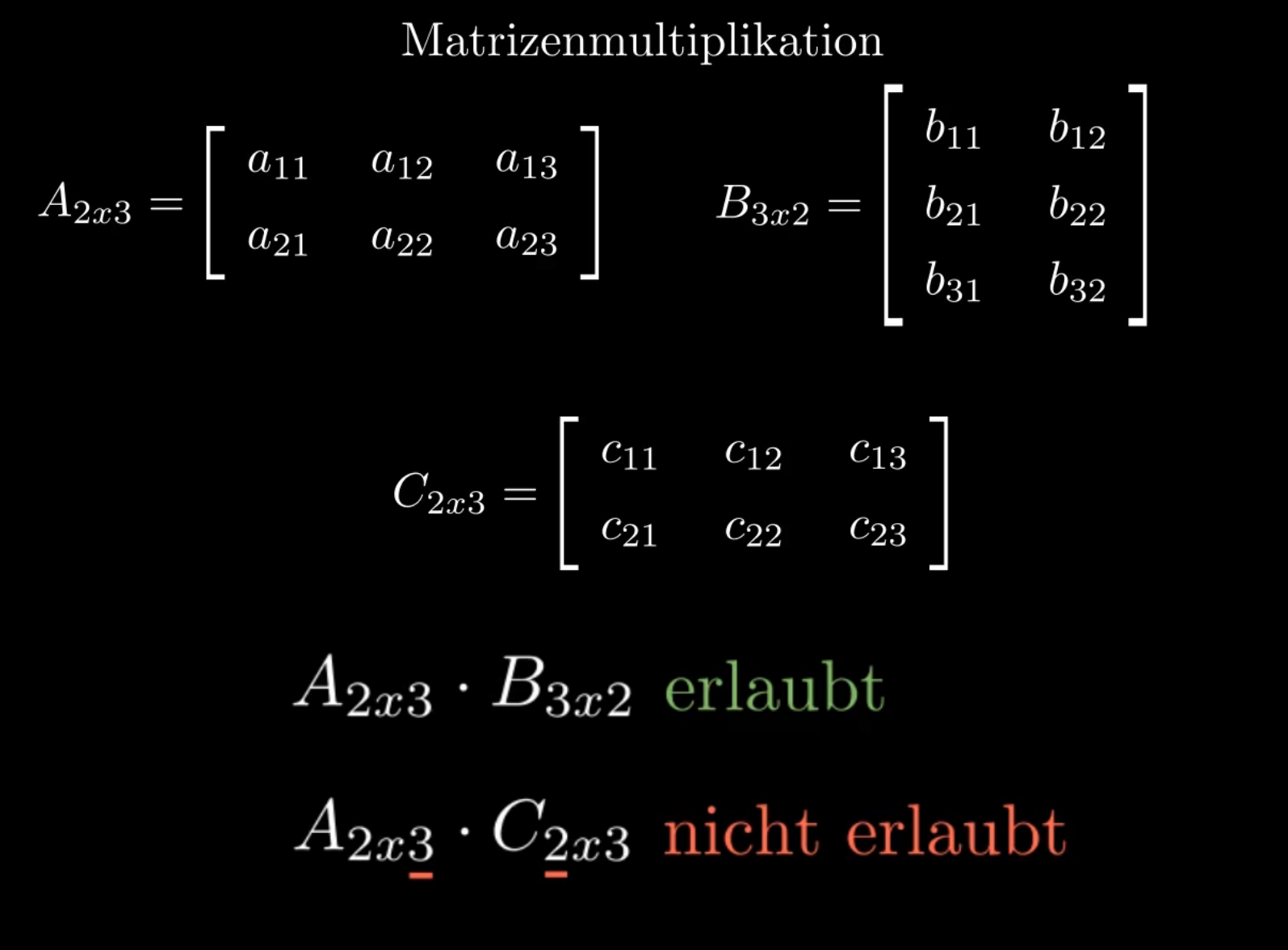
Damit man zwei Matrizen multiplizieren darf, muss die Spaltenzahl der ersten Matrix mit der Zeilenzahl der zweiten Matrix übereinstimmen.
Beispiel
\(A=\begin{pmatrix}\textcolor{green}{a_{11}} & \textcolor{green}{a_{12}} & \textcolor{green}{a_{13}} & \textcolor{green}{a_{14}} \\a_{21} & a_{22} & a_{23} & a_{24} \\\end{pmatrix}\)
\(B=\begin{pmatrix}\textcolor{green}{b_{11}} & b_{12} \\\textcolor{green}{b_{11}} & b_{22} \\\textcolor{green}{b_{31}} & b_{32}\\\textcolor{green}{b_{41}} & b_{42} \\\end{pmatrix}\)
Eine Multiplikation von Matrix A und Matrix B ist möglich weil die Spaltenanzahl von A und die Zeilenanzahl von B gleich sind.
Beispiel
\(C=\begin{pmatrix}\textcolor{red}{a_{11}} & \textcolor{red}{a_{12}} & \textcolor{red}{a_{13}} \\a_{21} & a_{22} & a_{23} \\\end{pmatrix}\)
\(D=\begin{pmatrix}\textcolor{red}{b_{11}} & b_{12} \\\textcolor{red}{b_{11}} & b_{22} \\\end{pmatrix}\)
Eine Multiplikation von Matrix C und Matrix D ist nicht möglich weil die Spaltenanzahl von A und die Zeilenanzahl von B unterschiedlich sind.
Wie kann man Matrizen Multiplizieren?
Um zu verstehen wie man Matrizen Multiplizieren kann, betrachten wir die folgenden Beispiele.
Beispiel 1
\(A=\begin{pmatrix}a_{11} & a_{12} \\a_{21} & a_{22} \\\end{pmatrix}\)
\(B=\begin{pmatrix}b_{11} & b_{12} \\b_{21} & b_{22}\\\end{pmatrix}\)
\(A\cdot B=\begin{pmatrix}a_{11}\cdot b_{11}+a_{12}\cdot b_{21} && a_{11}\cdot b_{12}+a_{12}\cdot b_{22}\\a_{21}\cdot b_{11}+a_{22}\cdot b_{21} && a_{21}\cdot b_{12}+a_{22}\cdot b_{22} \\\end{pmatrix}\)
Beispiel 2
\(A=\begin{pmatrix}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23} \\\end{pmatrix}\)
\(B=\begin{pmatrix}b_{11} & b_{12} \\b_{21} & b_{22} \\b_{31} & b_{32}\\\end{pmatrix}\)
\(A\cdot B=\)
\(\begin{pmatrix}a_{11}\cdot b_{11}+a_{12}\cdot b_{21}+a_{13}\cdot b_{31} & a_{11}\cdot b_{12}+a_{12}\cdot b_{22}+a_{13}\cdot b_{32} \\a_{21}\cdot b_{11}+a_{22}\cdot b_{21}+a_{23}\cdot b_{31} & a_{21}\cdot b_{12}+a_{22}\cdot b_{22}+a_{23}\cdot b_{32} \\\end{pmatrix}\)
Rechenregeln der Matrixmultiplikation
Die Multiplikation von Matrizen ist Assoziativ und Distributiv.
Matrix Multiplikation ist Assoziativ
\((A\cdot B)\cdot C=A\cdot (B\cdot C)\)
Matrix Addition ist Distributiv
\(A\cdot (B+C)=(A\cdot B)+(A\cdot C)\)
\((A+B)\cdot C=(A\cdot C)+(B\cdot C)\)
Achtung !
Im Allgemeinen gilt:
\(A\cdot B \neq B\cdot A\)
Matrizenmultiplikation Eigenschaften
Eine wichtige Eigenschaft der Matrix Multiplikation besteht darin, das die Multiplikation nicht Kommutativ ist. Das bedeutet:
\(A\cdot B\neq B\cdot A\)
Man darf die Matrizen also nicht vertauschen. Diese Eigenschaft kann man an einem einfachen Beispiel nachvollziehen:
Beispiel
\(\begin{aligned} &A\cdot B=\begin{pmatrix} 1 & 1 \\ 0 & 1 \\\end{pmatrix}\cdot \begin{pmatrix} 1 & 0 \\ 1 & 1 \\\end{pmatrix}= \begin{pmatrix} 2 & 1 \\ 1 & 1 \\\end{pmatrix}\\ \\ &B\cdot A=\begin{pmatrix} 1 & 0 \\ 1 & 1 \\\end{pmatrix}\cdot \begin{pmatrix} 1 & 1 \\ 0 & 1 \\\end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 1 & 2 \\\end{pmatrix} \end{aligned}\)
Wir sehen also, dass \(A\cdot B\) nicht das gleich ist wie \(B\cdot A\). Darüber hinaus muss \(B\cdot A\) nicht definiert sein, nur weil \(A\cdot B\) definiert ist. Das ist beispielsweise der Fall, wenn \(A\) eine 2x3-Matrix ist und \(B\) eine 3x4 Matrix ist. In diesem Fall wäre die Multiplikation \(B\cdot A\) nicht definiert, weil \(A\) nicht zu viele Zeilen besitzt wie \(B\) Spalten.
Matrix Determinante Berechnen
Du Möchtest wissen wie man die Determinante einer Matrix berechnen kann? Dann werf einen Blick auf den Beitrag Determinante einer Matrix berechnen.
