Determinante - Regel von Sarrus
Determinanten Rechner
Der Matrizen Rechner von Simplexy kann beliebige Matrix Rechenoperationen für dich durchführen. Mit dem Rechner kannst du unter anderen die Determinante berechnen und viel mehr.
Regel von Sarrus
In diesem Beitrag wirst du lernen wie man für eine 3x3 Matrix die Determinante berechnen kann. Für die Berechnung einer Determinante für eine 3x3 Matrix kann man die Regel von Sarrus anwenden.
Regel von Sarrus einfach erklärt
\(A=\begin{pmatrix}a & b & c\\d & e & f \\ g & h & i \\\end{pmatrix}\)
Die Regel von Sarrus ist eine hilfreiche Regel bei der Berechnung von 3x3 Determinanten. Man schreibt die ersten zwei Spalten als Erweiterung rechts neben der Matrix und bildet das Produkt der drei Diagonalen.
\(|A|=\begin{vmatrix}a & b & c\\d & e & f \\ g & h & i \\\end{vmatrix}\begin{matrix}a & b \\d & e \\ g & h \\\end{matrix}\)
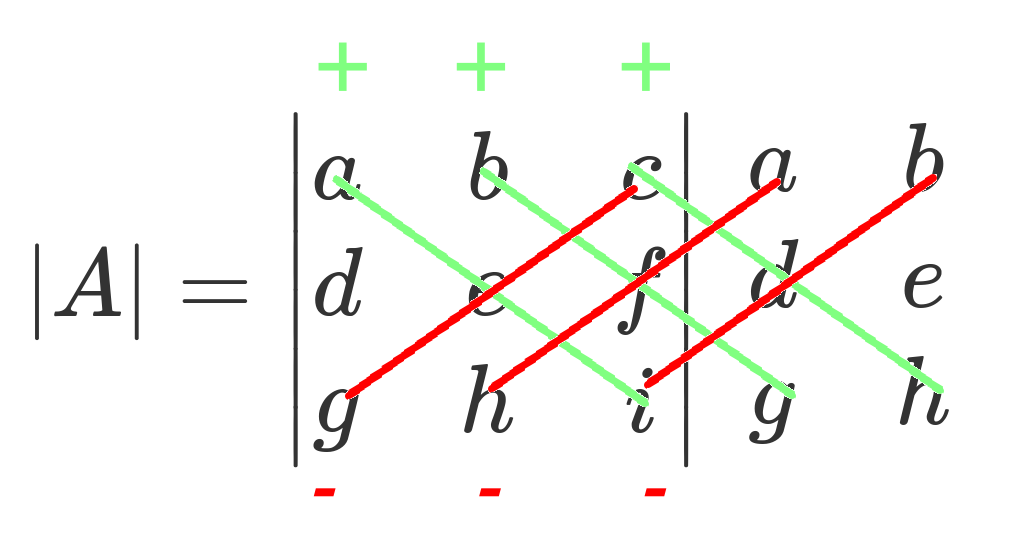
Wie in dem Video dargestellt berechnet man das Produkt aus den drei Diagonalen, die von oben links nach unten rechts verlaufen.
\(a\cdot e\cdot i+b\cdot f\cdot g+c\cdot d\cdot h\)
Man berechnet anschießend das Produkt aus den drei Diagonalen, die von unten links nach oben rechts verlaufen.
\(-g\cdot e\cdot c -h\cdot f\cdot a-i\cdot d\cdot b\)
Nun werden die zwei Produkte aus den Diagonalen von einander abgezogen.
\(|A|=\begin{vmatrix}a & b & c\\d & e & f \\ g & h & i \\\end{vmatrix}=\)
\(a\cdot e\cdot i+b\cdot f\cdot g+c\cdot d\cdot h-g\cdot e\cdot c -h\cdot f\cdot a-i\cdot d\cdot b\)
Regel von Sarrus
Die Determinante einer 3x3 Matrix kann mittels Regel von Sarrus berechnet werden.
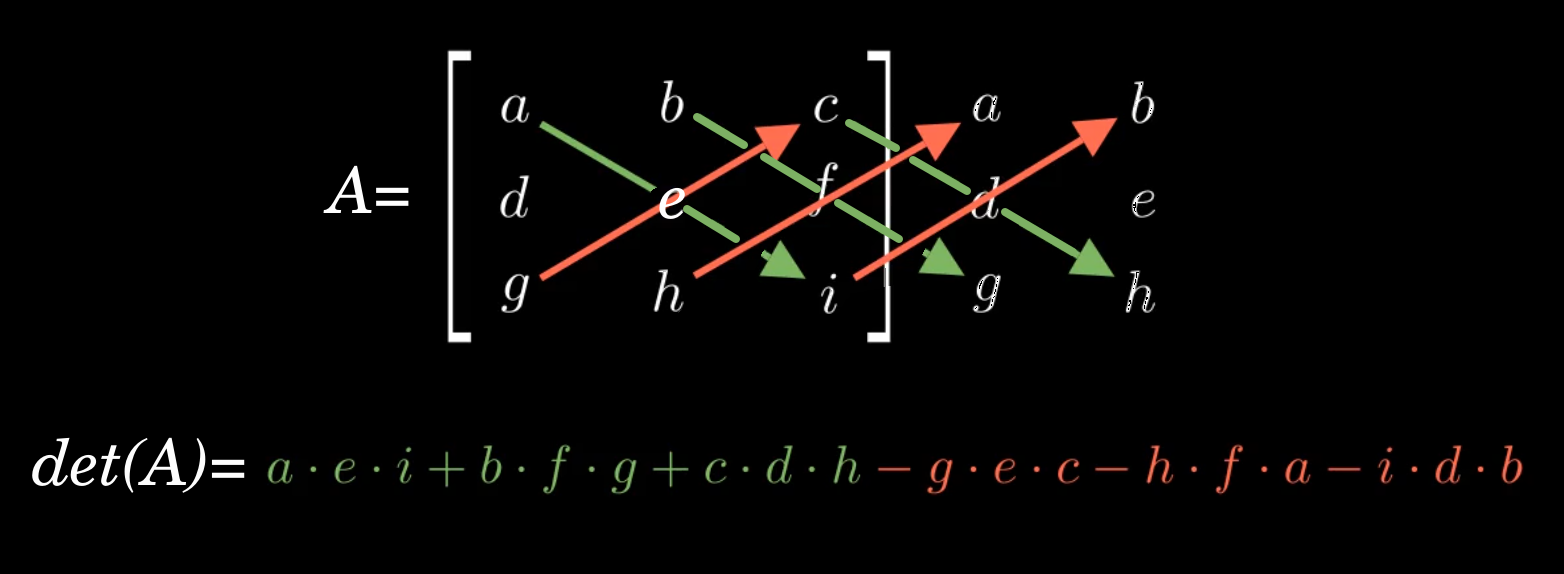
Die Regel von Sarrus ist nur eine Veranschaulichung des Laplace'sche Entwicklungssatzes. Die Regel von Sarrus, in der hier beschrieben Form, kann nur auf 3x3 Matrizen angewandt werden.
Regel von Sarrus Beispiel
Gegeben ist die folgende 3x3 Matrix \(A\). Berechne die Determinante \(det(A)\).
Lösung
Für die Berechnung der Determinante werden wir die Regel von Sarrus anwenden:
\(A=\begin{pmatrix}1 & 2 & 3\\4 & 5 & 6 \\ 7 & 8 & 9 \\\end{pmatrix}\)
\(|A|=\begin{vmatrix}1 & 2 & 3\\4 & 5 & 6 \\ 7 & 8 & 9 \\\end{vmatrix}\)
\(=\textcolor{green}{1\cdot 5\cdot 9+2\cdot 6\cdot 7+3\cdot 4\cdot 8}\textcolor{red}{-7\cdot 5\cdot 3-8\cdot 6\cdot 1-9\cdot 4\cdot 2}\)
\(=45+84+96-105-48-72=0\)
Damit folgt für die Determinante der 3x3 Matrix \(A\):
\(det(A)\)=0
