Ortsvektor und Richtungsvektor
Vektorrechner
Der Online Vektorrechner von Simplexy kann viele Vektoroperationen für dich durchführen.
Ortsvektor und Richtungsvektor
Betrachten wir den Koordinatenursprung \(O(0|0)\) und den Punkt \(P(4|2)\), der Vektor \(\overrightarrow{OP}=\vec{p}=\left(\begin{array}{c} 4-0 \\ 2-0\end{array}\right)=\left(\begin{array}{c} 4 \\ 2\end{array}\right)\) nennt man Ortsvektor zum Punkt \(P\).
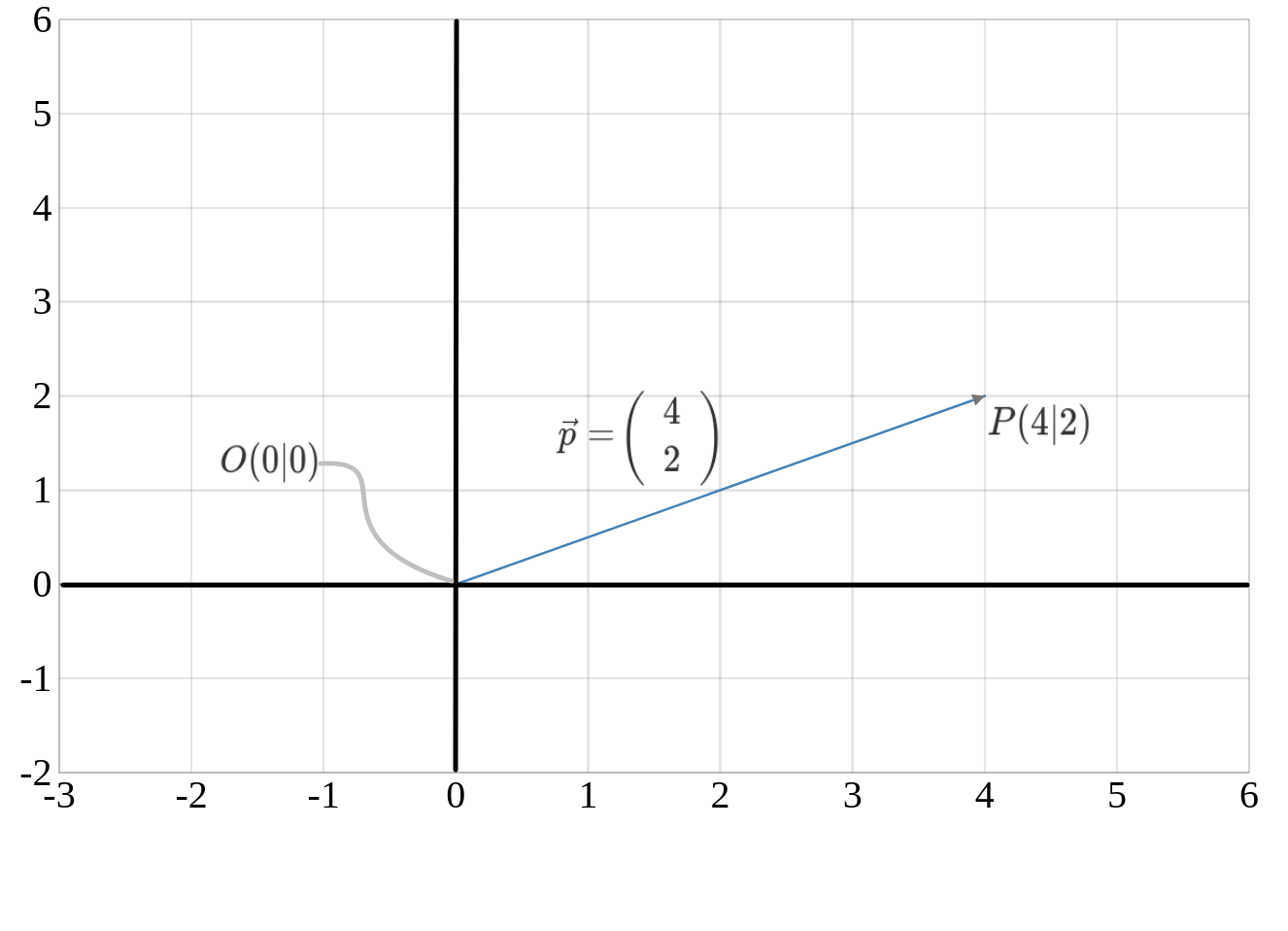
Ein Ortsvektor hat immer den Koordinatenursprung als Startpunkt und die Spitze zeigt immer auf den gewünschten Endpunkt. Ein Richtungsvektor hingegen kann jeden Punkt als Startpunkt besitzen. Zum Beispiel ist der Richtungsvektor zwischen den Punkten \(A(1|3)\) und \(B(4|1)\) gegeben über:
\(\overrightarrow{AB}=\vec{b}-\vec{a}=\left(\begin{array}{c} 4 \\ 1\end{array}\right)-\left(\begin{array}{c} 1 \\ 3\end{array}\right)=\left(\begin{array}{c} 4-1 \\ 1-3\end{array}\right)=\left(\begin{array}{c} 3 \\ -2\end{array}\right)\)
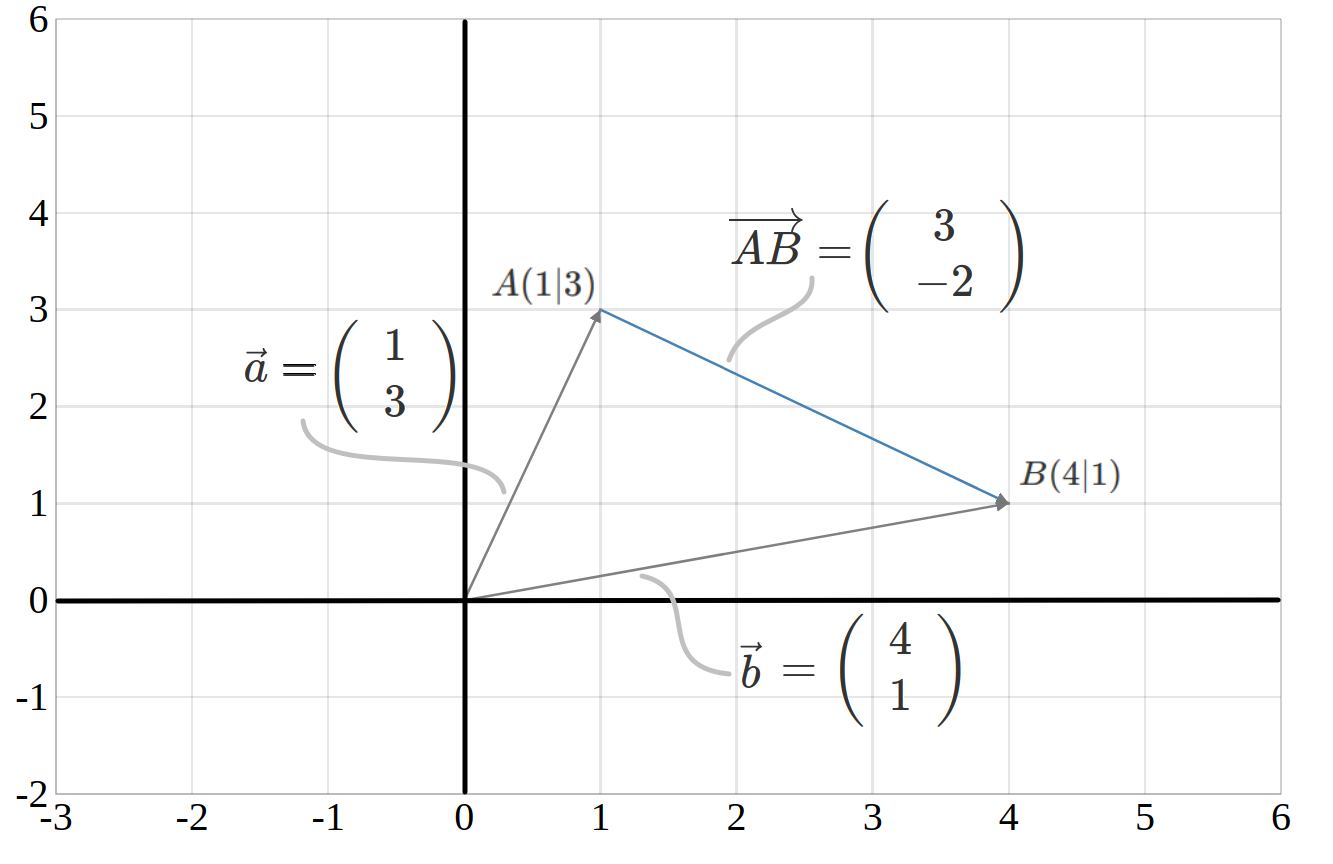
Wenn zwei Richtungsvektoren die gleiche Länge und die gleiche Richtung besitzen, dann sind sie identisch. Im dreidimensionalen Raum gilt das gleiche für die Richtungsvektoren wie im zwei-dimensionalen. Es kommt lediglich noch eine zusätzliche \(z\)-Achse in den Komponenten der Vektoren.
