Vektorrechnung Skalarprodukt
Skalarprodukt Rechner
Der Vektorrechner von Simplexy kann beliebige Vektoroperationen für dich durchführen. Mit dem Rechner kannst du den Winkel zwischen Vektoren berechnen, Vektoren addieren, Vektoren subtrahieren, Skalarprodukt berechnen, Kreuzprodukt berechnen und viel mehr.
Das Skalarprodukt
Das Skalarprodukt (inneres Produkt) ist eine mathematische Rechenoperation, bei der zwei Vektoren einer Zahl zugeordnet werden. Die Zahl, die man erhält entspricht der Länge der Projektion des einen Vektors auf den anderen.
Regel:
Skalarprodukt Formel
Im zwei-Dimensionalen:
\(\vec{a}\bullet \vec{b}=a_1\cdot b_1+a_2\cdot b_2\)
Im drei-Dimensionalen:
\(\vec{a}\bullet \vec{b}=a_1\cdot b_1+a_2\cdot b_2+a_3\cdot b_3\)
Beispiel
\(\left(\begin{array}{c} 2 \\ 3\end{array}\right)\bullet\left(\begin{array}{c} 5 \\ 1\end{array}\right)=2\cdot 5+3\cdot 1=13\)
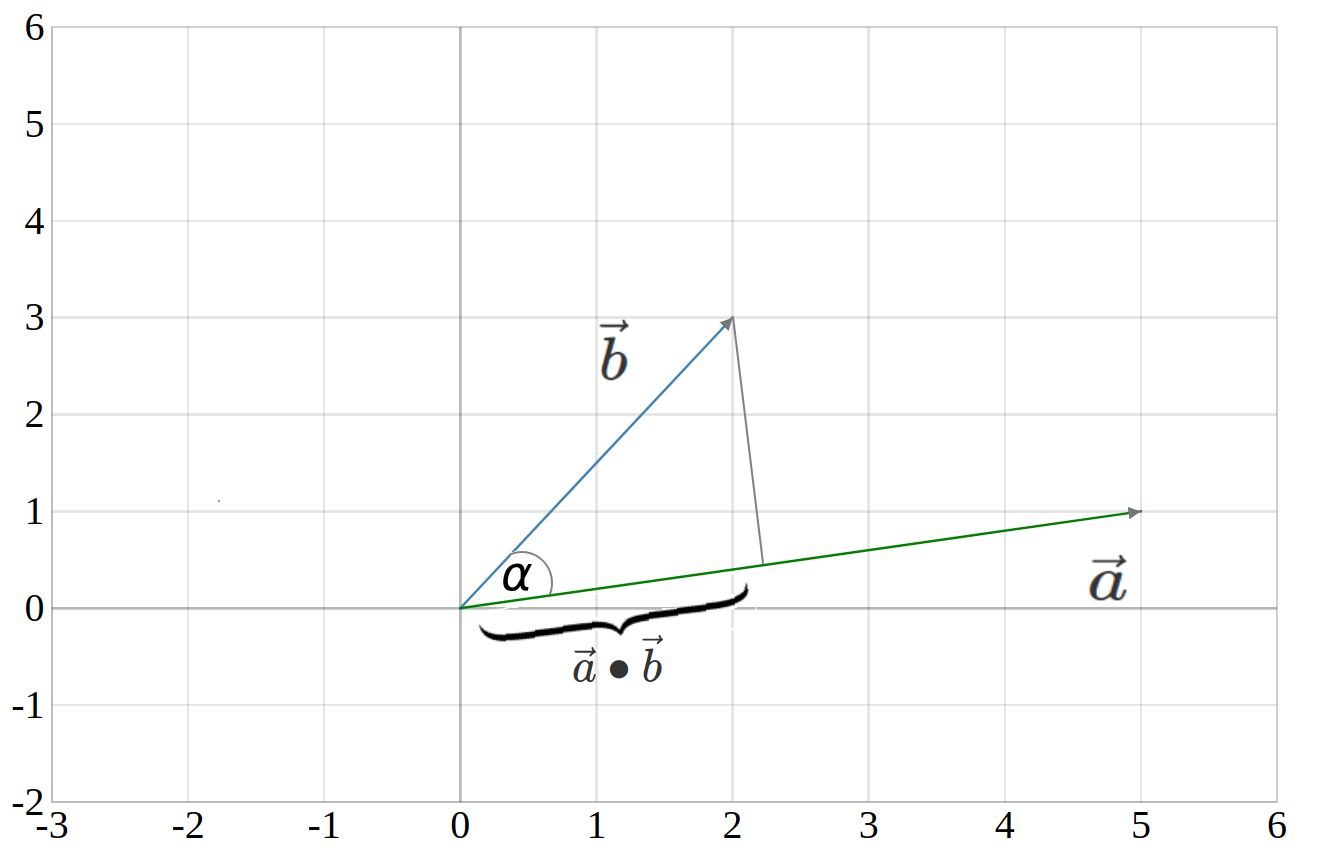
Aus der oberen Abbildung kannst du bereits entnehmen, dass das Skalarprodukt vom Winkel zwischen den zwei Vektoren abhängt. Je größer der Winkel zwischen den Vektoren ist, desto kleiner ist die Projektion des einen Vektors auf den anderen und damit ist auch das Skalarpodukt an sich kleiner.
Der Zusammenhang zwischen dem Winkel zwischen den Vektoren und der Projektion des einen Vektors auf den anderen wird in der nächsten Abbildung vedeutlicht.
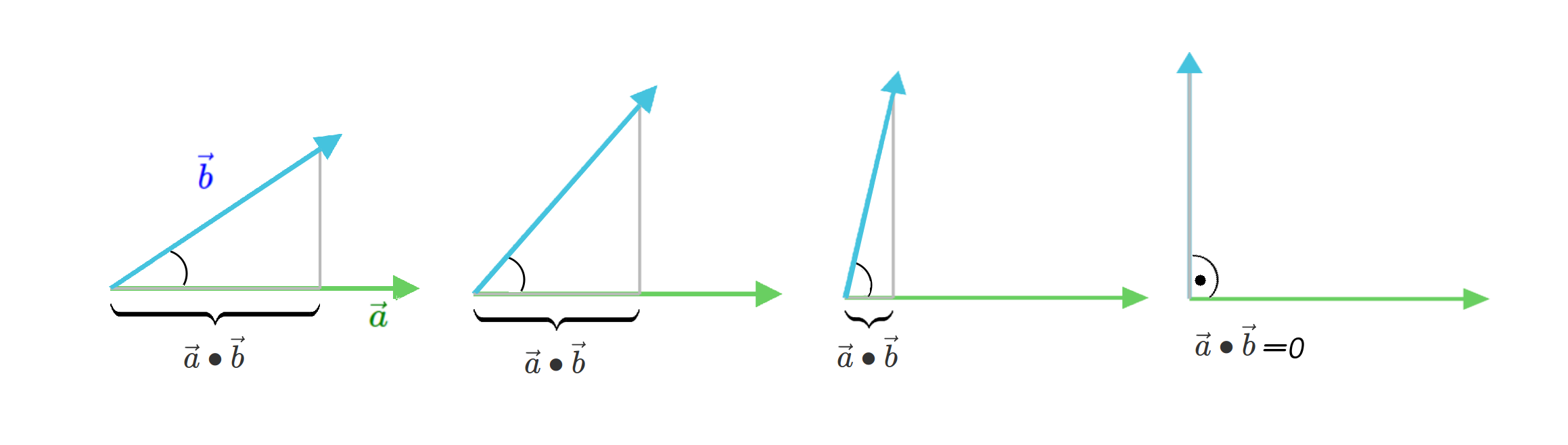
Wie du siehst ist die Projektion von Vektor \(\vec{b}\) auf \(\vec{a}\) vom Winkel zwischen den Vektoren abhängig. Je größer der Winkel zwischen ihnen ist, desto kleiner wird die Projektion von \(\vec{b}\) auf \(\vec{a}\) und damit wird auch das Skalarprodukt \(\vec{a}\bullet \vec{b}\) kleiner. Ist der Winkel zwischen den Vektoren \(90°\) dann gibt es keine Projektion von \(\vec{b}\) auf \(\vec{a}\), das Skalarprodukt ist Null.
Regel:
Skalarprodukt Winkelabhängigkeit
Im zwei-Dimensionalen gilt für den Winkel \(\alpha\) zwischen den Vektoren \(\vec{a}\) und \(\vec{b}\):
\(cos(\alpha)=\frac{\vec{a}\bullet \vec{b}}{|\vec{a}|\cdot |\vec{b}|}=\frac{a_1\cdot b_1+a_2\cdot b_2}{\sqrt{a_1^2+ a_2^2}\cdot\sqrt{b_1^2+ b_2^2}}\)
Im Dreidimensionalen gilt für den Winkel \(\alpha\) zwischen den Vektoren:
\(cos(\alpha)=\frac{\vec{a}\bullet \vec{b}}{|\vec{a}|\cdot |\vec{b}|}=\frac{a_1\cdot b_1+a_2\cdot b_2+a_3\cdot b_3}{\sqrt{a_1^2+ a_2^2+a_3^2}\cdot\sqrt{b_1^2+ b_2^2+b_3^2}}\)
Sowohl im zwei-Dimensionalen als auch im Dreidimensionalen erhält man den Winkel \(\alpha\) über:
\(\alpha=cos^{-1}\Big(\frac{\vec{a}\bullet \vec{b}}{|\vec{a}|\cdot |\vec{b}|}\Big)\)
Beispiel
Winkel zwischen den Einheitsvektoren \(\vec{e_x}\) und \(\vec{e_y}\):
\(\vec{e_x}=\left(\begin{array}{c} 1 \\ 0\\0\end{array}\right)\) \(\vec{e_y}=\left(\begin{array}{c} 0 \\ 1\\0\end{array}\right)\)
Den Winkel \(\alpha\) zwischen \(\vec{e_x}\) und \(\vec{e_y}\) erhalten wir über:
\(\alpha=cos^{-1}\Big(\frac{\vec{e_x}\bullet \vec{e_y}}{|\vec{e_x}|\cdot |\vec{e_y}|}\Big)\)
Wir wissen bereits, das \(\vec{e_x}\bullet \vec{e_y}=0\) damit folgt für den Winkel zwischen den Einheitsvektoren:
\(\alpha=cos^{-1}(0)=90°\)
Da die Einheitsvektoren orthogonal zu einander sind ist es kein Wunder, dass zwischen ihnen ein Winkel von \(90°\) liegt.
