Lineare Funktion Normalform
Lineare Funktion Rechner
Der Online Rechner mit Rechenweg von Simplexy kann lineare Funktionen zeichnen, Nullstellen berechnen, Y-Achsenabschnitte berechnen und viel mehr.
Lineare Funktion Normalform
Die Normalform einer Linearen Funktion lautet
\(f(x)=m\cdot x+b\)
Der Graph einer Linearen Funktion ist wie der Name schon sagt eine Gerade. Dabei nennt man \(m\) die Steigung der Geraden und \(b\) nennt man den \(y\)-Achsenabschnitt, also die Stelle an der die Gerade die \(y\)-Achse schneidet. In einem Koordinantensystem wird das aussehen der Geraden, durch die Werte \(m\) und \(b\) festgelegt.
Normalform Beispiel
In der folgegnden Abbildung der der Graph der linearen Funktion \(f(x)=2\cdot x + 1\) abgebildet.
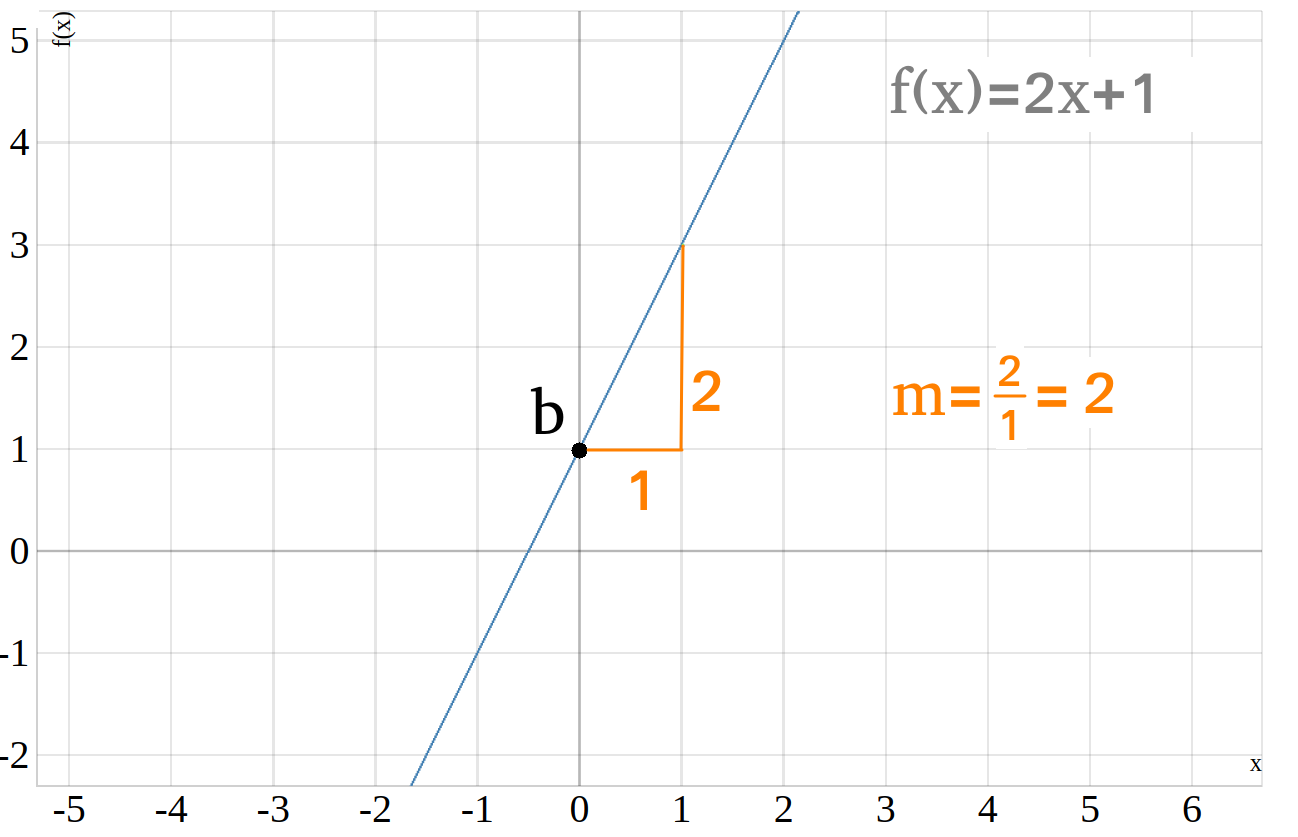
Wobei hier \(m=2\) und \(b=1\) ist. Dabei ist \(m\) die Steigung und \(b\) der y Achsenabschnitt der Geraden.
Solche Graphen kannst du mit dem online Rechner für lineare Funktionen von Simplexy selber erstellen, gib in das Eingabefeld zum Beispiel \(2\cdot x + 1\) ein und siehe was passiert. Hier kommst du zum Rechner für lineare Funktionen.
Normalform y Achsenabschnitt
\(f(x)=m\cdot x+\textcolor{red}{b}\)
Der y Achsenabschnitt \(\textcolor{red}{b}\) einer linearen Funktion gibt an, wo der Graph die \(y\)-Achse schneidet.
In dem obigen Graphen siehst du bereits wie man auf den Wert von \(b\) kommt, wenn dir nur der Graph gegeben ist. Dazu musst du lediglich rausfinden an welcher Stelle eine Gerade die \(y\)-Achse schneidet. Dort liegt der Schnittpunkt mit der y Achse am Punkt \((0|1)\). In einem Koordinantensystem werden Punkte immer durch die Angabe \((x|y)\) dargestellt.
Solche Graphen kannst du mit dem online Rechner für lineare Funktionen von Simplexy selber erstellen, gib in das Eingabefeld zum Beispiel \(2\cdot x + 1\) ein und siehe was passiert. Hier kommst du zum Rechner für Geraden.
Der \(y\)-Achsenabschnitt einer Geraden kann auch negativ sein, das kannst du am zweiten Beispiel sehen.
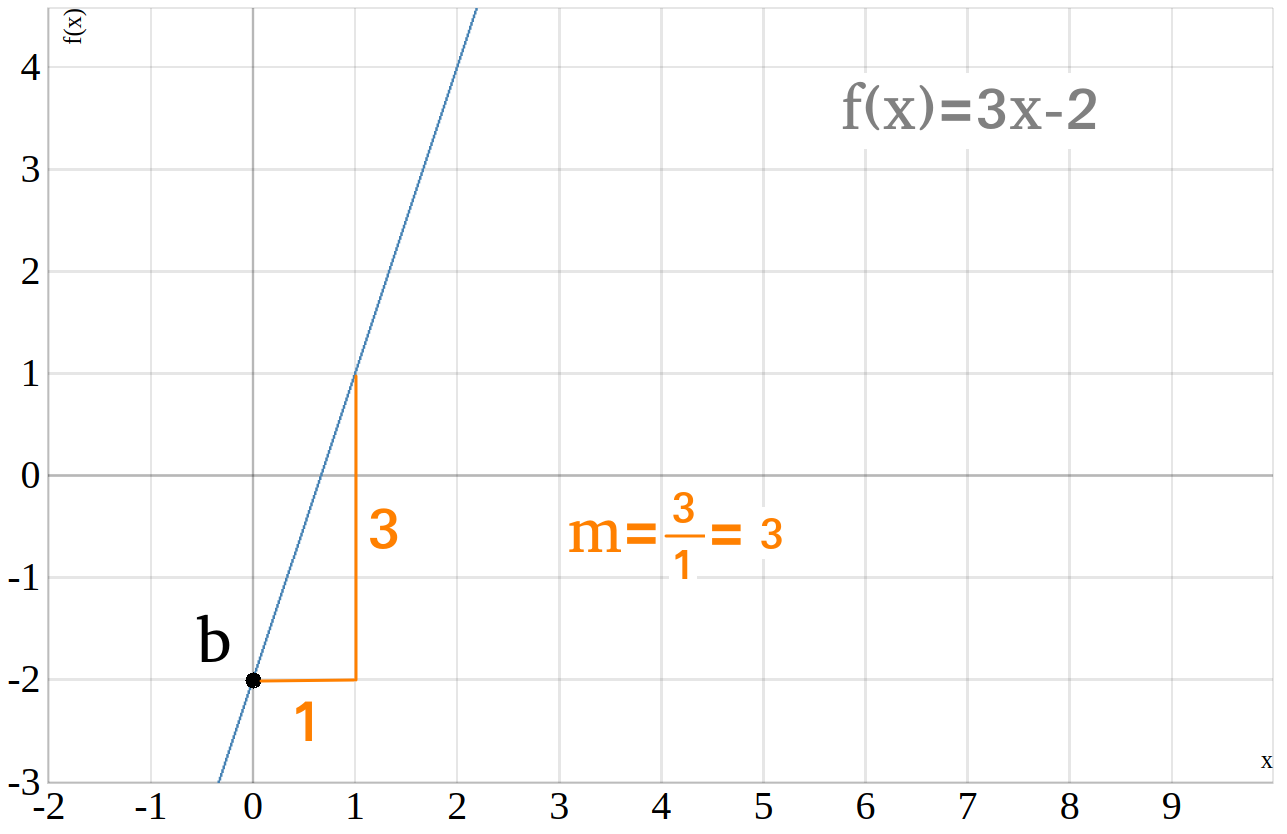
Wie du in dem Graphen oben siehst, lautet die Funktionsgleichung dieser Geraden
\(f(x)=3\cdot x - 2\).
Da die Gerade die \(y\)-Achse am punkt \((0|-2)\) schneidet, ist der \(y\)-Achsenabschnitt der Funktion \(b=-2\).
Abgesehen von einem negativen \(y\)-Achsenabschnitt kann eine lineare Funktion auch eine negative Steigung besitzen. Dazu weiter unten mehr...
Merke
In der Funktionsgleichung einer linearen Funktion steht immer nur ein \(x\). Man findet keine höhere Potenz von \(x\), zb. \(x^2\) oder \(x^3\). Eine lineare Funktion wird daher auch als Funktion ersten Grades bezeichnet.
y Achsenabschnitt berechnen
Wenn du weitere Beispiele sehen möchtest, wie man den y Achsenabschnitt berechnen kann, so werf einen Blick auf den Beitrag y Achsenabschnitt berechnen.
Normalform Steigung
\(f(x)=\textcolor{blue}{m}\cdot x+b\)
Die Steigung \(\textcolor{blue}{m}\) gibt den Verlauf der Geraden an. Dabei gibt es drei Fälle die vorkommen:
Normalform Steigung
- Ist \(\textcolor{blue}{m}\) positiv, so steigt die lineare Funktion.
- Ist \(\textcolor{blue}{m}\) negativ, so fällt die lineare Funktion.
- Ist \(\textcolor{blue}{m}=0\), so hat mein eine konstante lineare Funktion.
Steigung berechnen
Betrachtet man nochmals die lineare Funktion \(f(x)=2\cdot x + 1\), so wissen wir bereits, dass die Steigung \(m=2\) ist. Wie kann man jedoch die Steigung einer linearen Funktion ermitteln, wenn lediglich der Graph der Funktion gegeben ist. Dazu muss man aussgehend vom \(y\)-Achsenabschnitt ein Quadrat bzw. eine Einheit nach rechts wandern und dann in \(y\)-Richtung solange nach oben gehen bis man die Gerade wieder erreicht. Um die Steigung der linearen Funktion zu berechnen muss man nun den folgenden Quotienten auswerten:
\(\begin{aligned} \frac{\Delta y}{\Delta x}=\frac{\text{Quadrate nach oben}}{\text{Quadrate nach rechts}} \end{aligned}\)
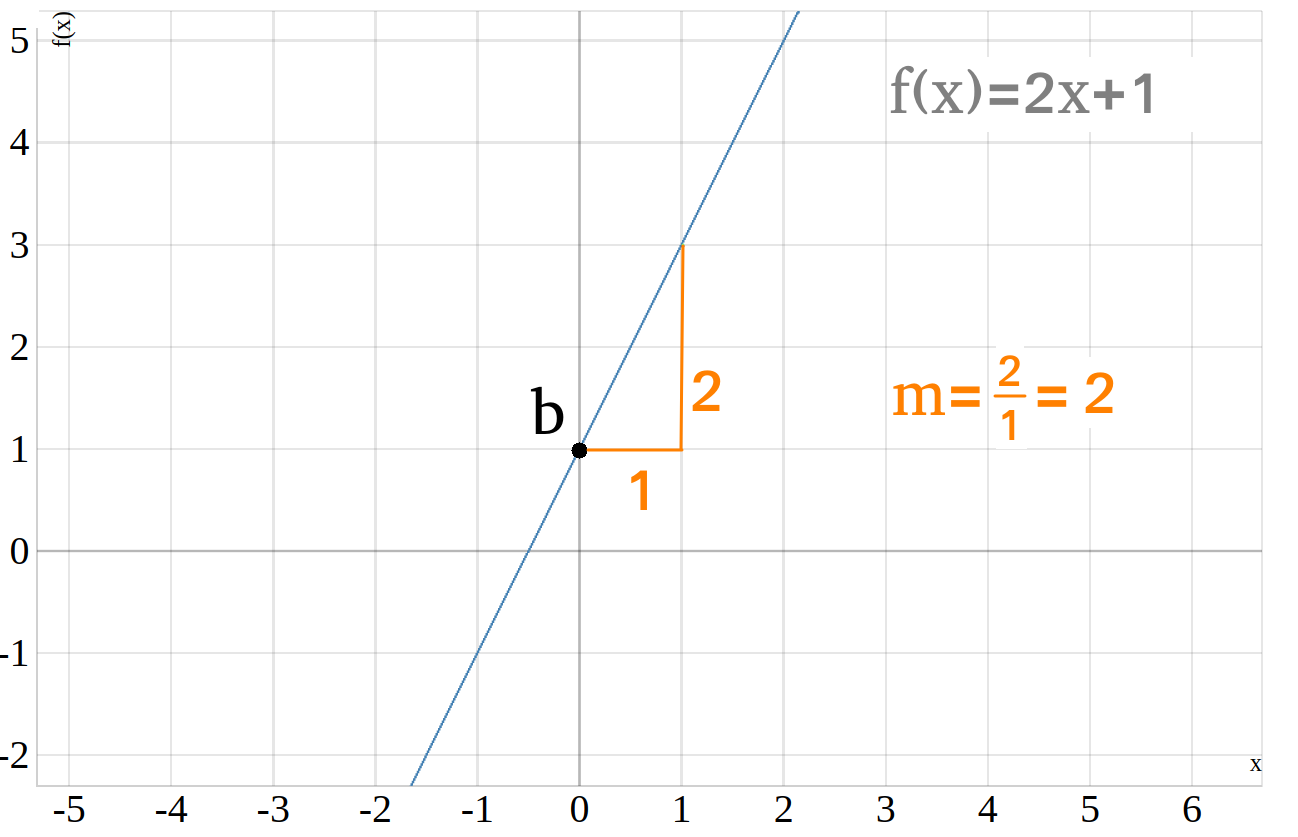
Ausgehend vom \(y\)-Achsenabschnitt muss man ein Quadrat nach rechts, und dann muss man genau zwei Quadrate nach oben gehen um auf die Gerade zu treffen.
Das heißt \(\Delta x = 1\) und \(\Delta y = 2\), der Quotient \(\frac{\Delta y}{\Delta x}\) aus beiden ist also
\(\frac{2}{1}=2\).
Das von \(\Delta x\) und \(\Delta y\) aufgespanntes Dreieck wird Steigungsdreieck genannt.
