Lineare Funktion Nullstelle berechnen
Lineare Funktion Rechner
Der Online Rechner mit Rechenweg von Simplexy kann lineare Funktionen zeichnen, Nullstellen berechnen, Y-Achsenabschnitte berechnen und viel mehr.
Nullstelle einer linearen Funktion berechnen
Was ist eine Nullstelle ?
Die Nullstelle einer linearen Funktion ist der Punkt im Koordinatensystem, an dem die Gerade die \(x\)-Achse schneidet. Um die Nullstelle berechnen zu können, musst du lediglich die Funktionsgleichung mit Null gleichsetzen. Denn gesucht ist ja der Punkt an dem die Gerade den Wert \(f(x)=0\) bzw. \(y=0\) besitzt.
Beipsiel Nullstelle berechnen
Gegeben ist die lineare Funktion
\(\begin{aligned} f(x)=2\cdot x -3 \end{aligned}\)
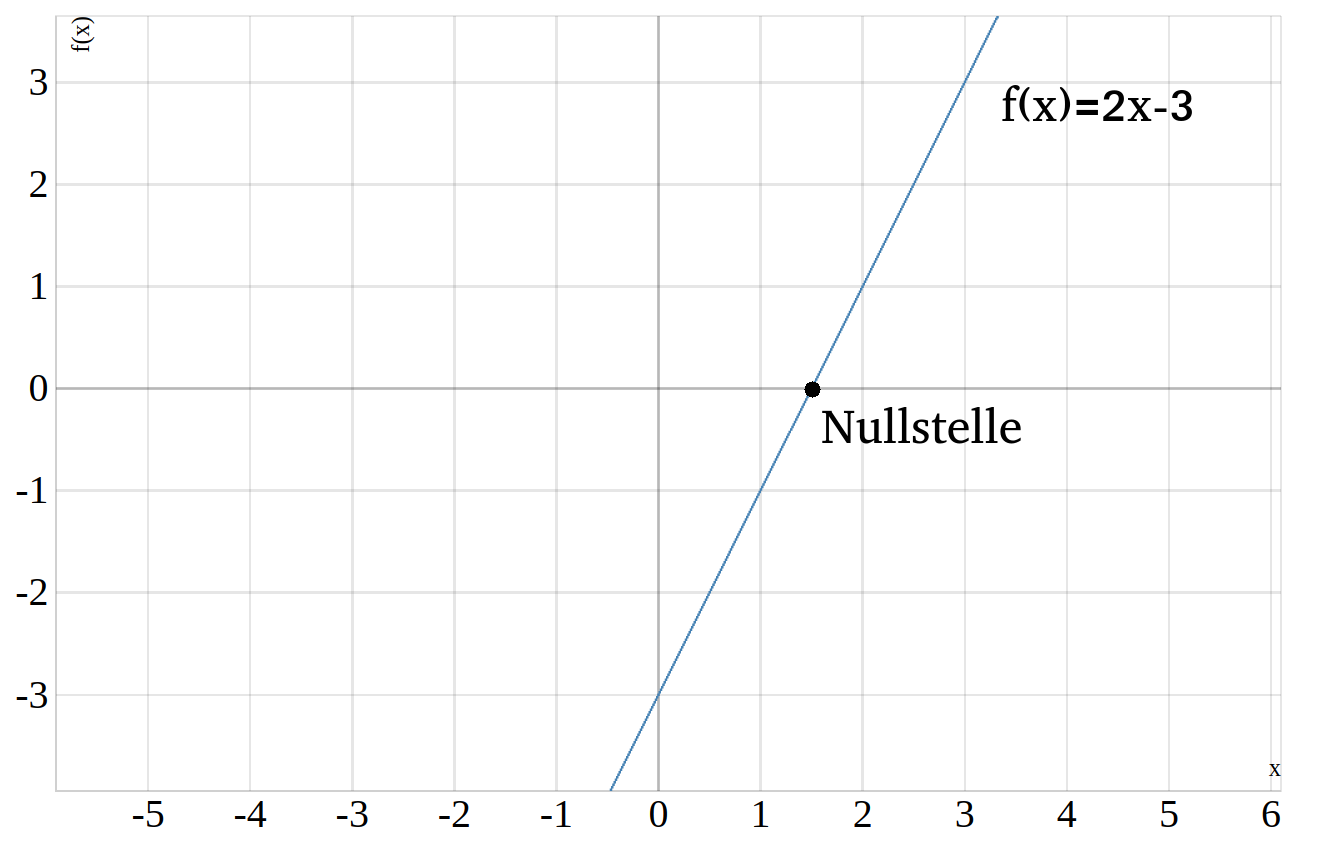
Berechne die Nullstelle der linearen Funktion.
Um die Nullstelle der linearen Funktion berechnen zu können, setzen wir die Funktionsgleichung gleich Null.
\(\begin{aligned} f(x)&=2\cdot x -3\\ \\ \textcolor{red}{0}&=2\cdot x -3 \end{aligned}\)
Nun müssen wir diese Gleichung nach \(x\) umstellen.
\(\begin{aligned} 0&=2\cdot x -3\,\,\,\,|+3\\ \\ 3&=2\cdot x\\ \\ 3&=2\cdot x\,\,\,\,|:2\\ \\ \frac{3}{2}&=x\\ \\ &\text{bzw.}\\ \\ x&=\frac{3}{2} \end{aligned}\)
Damit haben wir also als Nullstelle \(x=\frac{3}{2}=1,5\) ermittelt. Die dazugehörige Nullstelle \(S\) im Koordinatensystem lautet \(S=(0|\frac{3}{2})\).
Der y-Wert einer Nullstelle ist immer gleich Null
Lineare Funktion Nullstelle berechnen Vorgehen
Um die Nullstelle einer linearen Funktion berechnen zu können, muss man die Geradengleichung \(f(x)=m\cdot x+b\) Nullsetzt.
Dann muss man \(0=m\cdot x+b\) nach \(x\) umstellen.
Allgemein geschrieben ist die Nullstelle gegeben durch die Formel:
\(\begin{aligned} x=-\frac{b}{m} \end{aligned}\)
Solche Aufgaben kannst du mit dem Nullstellen berechner von Simplexy lösen. Der Rechner gibt dir die Lösung, einen Graphen und den Rechenweg an. Um die Nullstelle der Funktion \(f(x)=2\cdot x - 3\) zu bestimmt musst du im Eingabefeld \(2\cdot x -3 = 0\) eingeben, den rest erledigt der Rechner. So kannst du immer überprüfen ob du richtig gerechnest hast.
Nullstelle berechnen Beispiele:
Nun folgen ein paar Beispiele bzw. Aufgaben mit den jeweiligen Lösungen, zur Nullstellen Berechnung von linearen Funktionen.
Beispiele 1
Gegeben ist die lineare Funktion
\(\begin{aligned} f(x)=2\cdot x +1 \end{aligned}\)
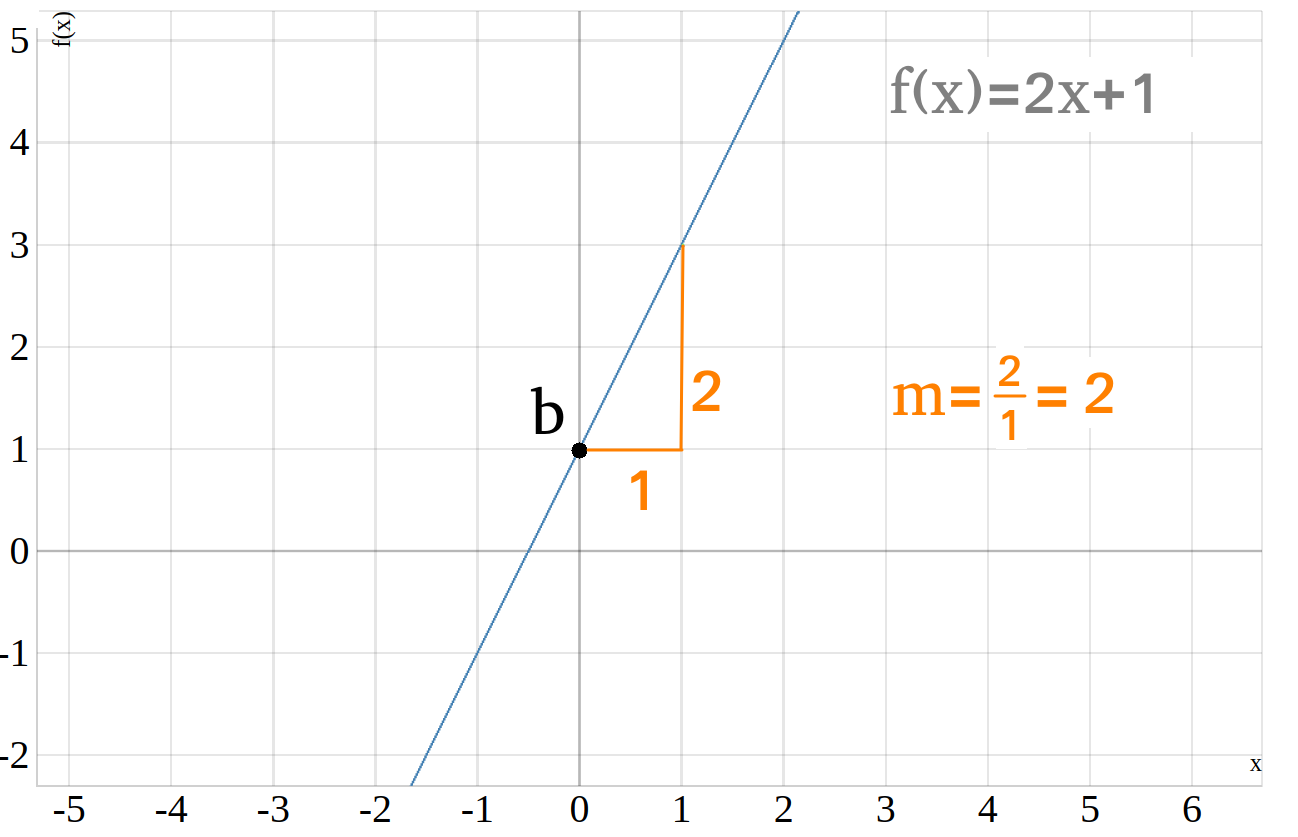
Berechne die Nullstelle der linearen Funktion.
Lösung
Um die Nullstelle berechnen zu können, müssen wir zunächst die Funktionsgleichung Nullsetzen.
\(\begin{aligned} f(x)&=2\cdot x +1\\ \\ 0&=2\cdot x +1 \end{aligned}\)
Nun müssen wir diese Gleichung nach \(x\) umstellen.
\(\begin{aligned} 0&=2\cdot x +1\\ \\ 0&=2\cdot x +1\,\,\,\,|-1\\ \\ -1&=2\cdot x\\ \\ -1&=2\cdot x\,\,\,\,|:2\\ \\ x&=-\frac{1}{2} \end{aligned}\)
Die Nullstelle der linearen Funktion liegt bei \(x=-\frac{1}{2}\). Der Schnittpunkt \(S\) der Geraden mit der \(x\)-Achse liegt also bei \(S=(0|-\frac{1}{2})\).
Beispiele 2
Gegeben ist die lineare Funktion
\(\begin{aligned} f(x)=3\cdot x -2 \end{aligned}\)
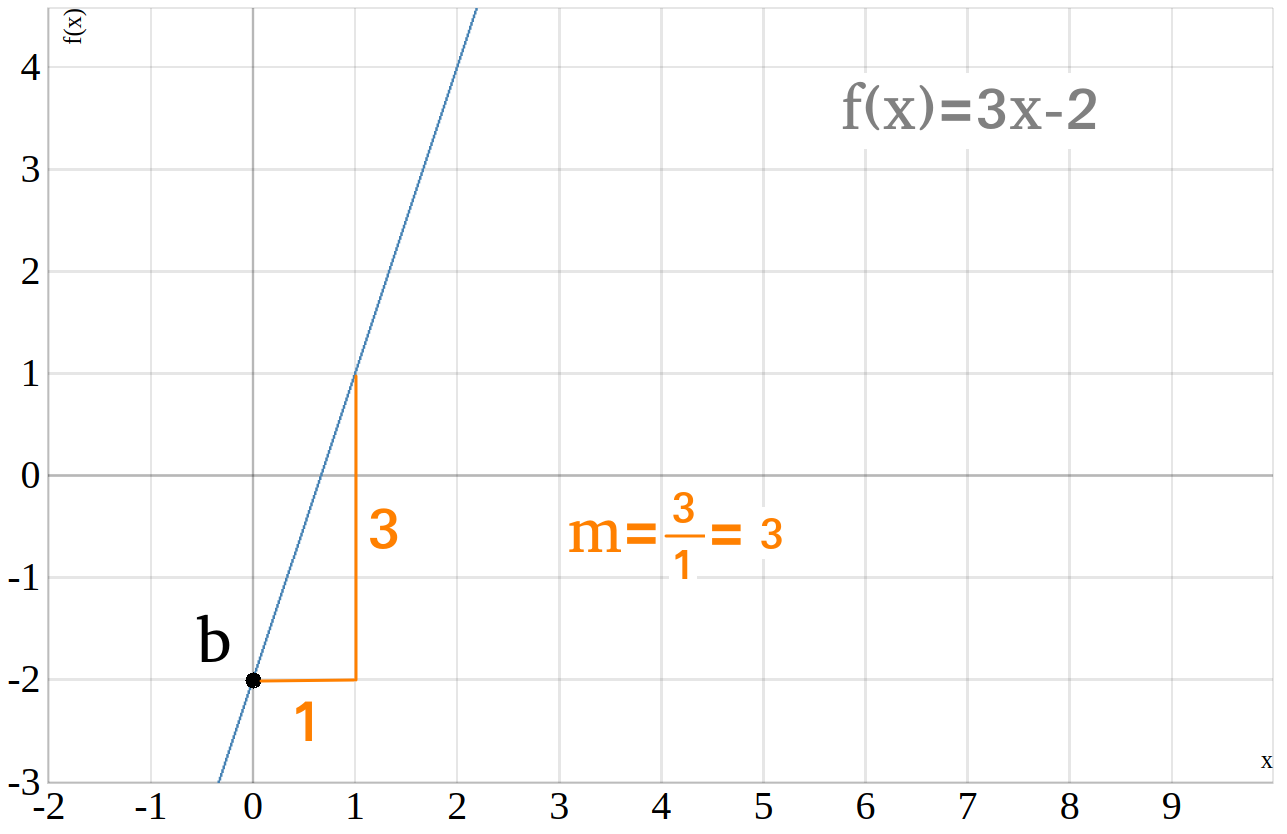
Wo befindet sich die Nullstelle der linearen Funktion?
Lösung
Um die Nullstelle berechnen zu können, müssen wir zunächst die Funktionsgleichung Nullsetzen.
\(\begin{aligned} f(x)&=3\cdot x -2\\ \\ 0&=3\cdot x -2 \end{aligned}\)
Nun müssen wir diese Gleichung nach \(x\) umstellen.
\(\begin{aligned} 0&=3\cdot x -2\\ \\ 0&=3\cdot x -2\,\,\,\,|+2\\ \\ 2&=3\cdot x\\ \\ 2&=3\cdot x\,\,\,\,|:3\\ \\ x&=\frac{2}{3} \end{aligned}\)
Die Nullstelle der linearen Funktion liegt bei \(x=\frac{2}{3}\). Der Schnittpunkt \(S\) der Geraden mit der \(x\)-Achse liegt also bei \(S=(0|\frac{2}{3})\).
