Lineare Funktion Steigung berechnen
Lineare Funktion Rechner
Der Online Rechner mit Rechenweg von Simplexy kannst du dir lineare Funktionen zeichnen lassen, Nullstellen berechnen, Y Achsenabschnitte berechnen, die Steigung berechnen und viel mehr.
Lineare Funktion
Eine Lineare Funktion hat ganz Allgemein die Form
\(f(x)=m\cdot x+b\)
Der Graph einer Linearen Funktion ist wie der Name schon sagt eine Gerade. Dabei nennt man \(m\) die Steigung der Geraden und \(b\) nennt man den \(y\)-Achsenabschnitt, also die Stelle an der die Gerade die \(y\)-Achse schneidet. In einem Koordinantensystem wird das aussehen der Geraden, durch die Werte \(m\) und \(b\) festgelegt.
Linearen Funktion Steigung
Hier siehst du den Graphen der Funktion \(f(x)=2\cdot x + 1\), in diesem fall ist \(m=2\) und \(b=1\)
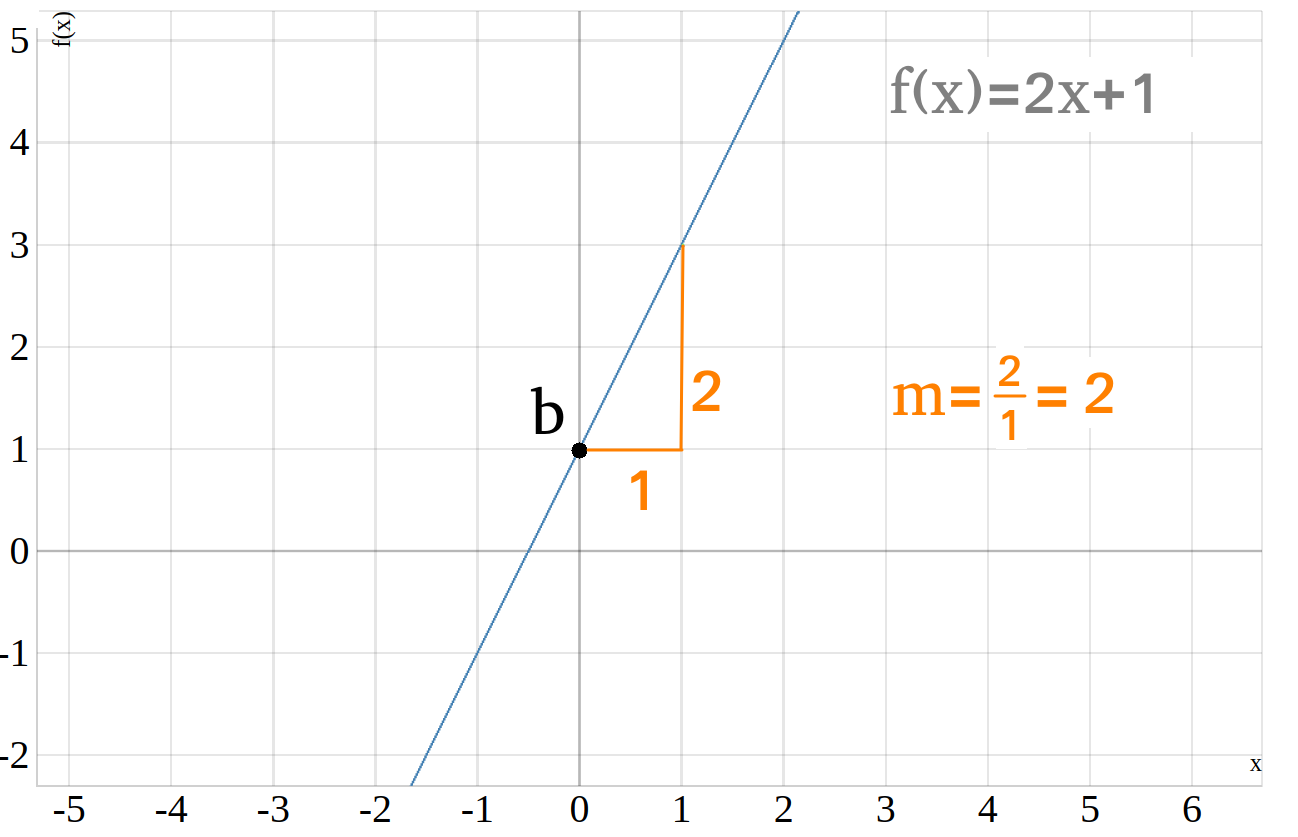
Du siehst bereits an der Funktionsgleichung \(f(x)=2\cdot x + 1\), dass die Steigung der linearen Funktion \(m=2\) ist, doch wie findet man das heraus wenn nur der Graph gegeben ist. Das ist ganz einfach, du musst aussgehend von deinem \(y\)-Achsenabschnitt ein Quadrat bzw. eine Einheit nach rechts gehen und dann in \(y\)-Richtung solange nach oben gehen bis du deine Gerade wieder triffst. Du musst dir jetzt nur noch merken wie viele Quadrate du nach rechts und wie viele Quadrate du nach oben gegangen bist. Die Steigung bekommst du dann indem du den quotienten
\(\begin{aligned} \frac{\Delta y}{\Delta x}=\frac{\text{Quadrate nach oben}}{\text{Quadrate nach rechts}} \end{aligned}\)
bestimmst.
Im Beispiel von Oben gehst du ausgehend vom \(y\)-Achsenabschnitt ein Quadrat nach rechts, und dann muss man genau zwei Quadrate nach oben gehen um auf die Gerade zu treffen.
Das heißt \(\Delta x = 1\) und \(\Delta y = 2\), der Quotient \(\frac{\Delta y}{\Delta x}\) aus beiden ist also
\(\frac{2}{1}=2\).
Damit ist also die Steigung der Funktion \(m=2\).
Negative Steigung
Eine Lineare Funktion kann auch eine negative Steigung besitzen, das heißt lediglich dass die Gerade mit größern \(x\)-Werte im kleinere \(y\)-Werte erreicht.
Hier siehst du eine Funktion mit negativer Steigung:
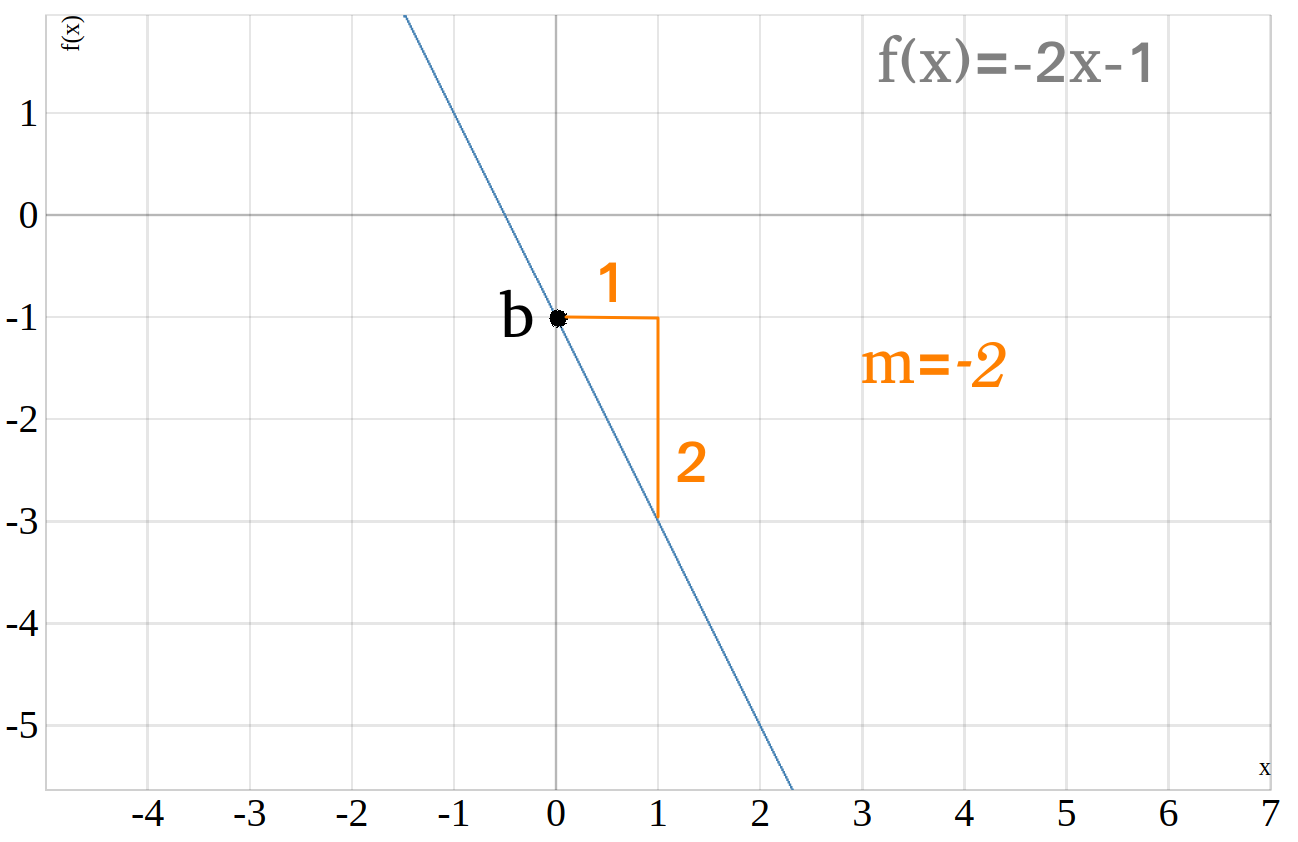
In diesem Beispiel ist die Funktion \(f(x)=-2\cdot x - 1 \), die Steigung
\(m=-2\) und der \(y\)-Achsenabschnitt \(b=-1\). Die Steigung dieser Geraden ist negativ weil die Funktion mit größeren \(x\)-Werten immer kleiner \(y\)-Werte annimmt. Anders als bei einer Funktion mit positiver Steigung ermitteln man die Steigung indem man eine Einheit nach rechts geht und dann so viele Quadrate nach unten geht bis man die Gerade wieder erreicht. Die Steigung berechnet sich bei einer linearen Funktion mit negativer Steigung folgendermaaßen:
\(\begin{aligned} m=-\frac{\Delta y}{\Delta x} \end{aligned}\)
Lineare Funktion Steigung berechnen
Die Steigung einer linearen Funktion berechnet sich über \(m=\frac{\Delta y}{\Delta x}\).
\(\Delta x\) ist die Anzahl an Einheit die man nach rechts geht. \(\Delta y\) ist die Anzahl an Einheiten die man von da aus benötigt um zur Gerade zu gelangen.
Die Steigung ist positiv wenn man nach oben gehen muss um zur Gerade zu gelangen.
Die Steigung ist negativ wenn man nach unten gehen muss um zur Gerade zu gelangen.
Steigung berechnen aus zwei Punkten
Sind lediglich zwei Punkte einer linearen Funktion gegeben, so kann man die Steigung der Geraden, welche durch diese zwei Punkte geht, berechnen.
Nehmen wir mal an, dir sind der Punkt \(Q=(-2|-4)\) und der Punkt \(P(2|2)\) gegeben. Wie erhält man die Steigunen der linearen Funktion, welche beide Punkte verbindet?
Zunächst einmal eine Skizze:
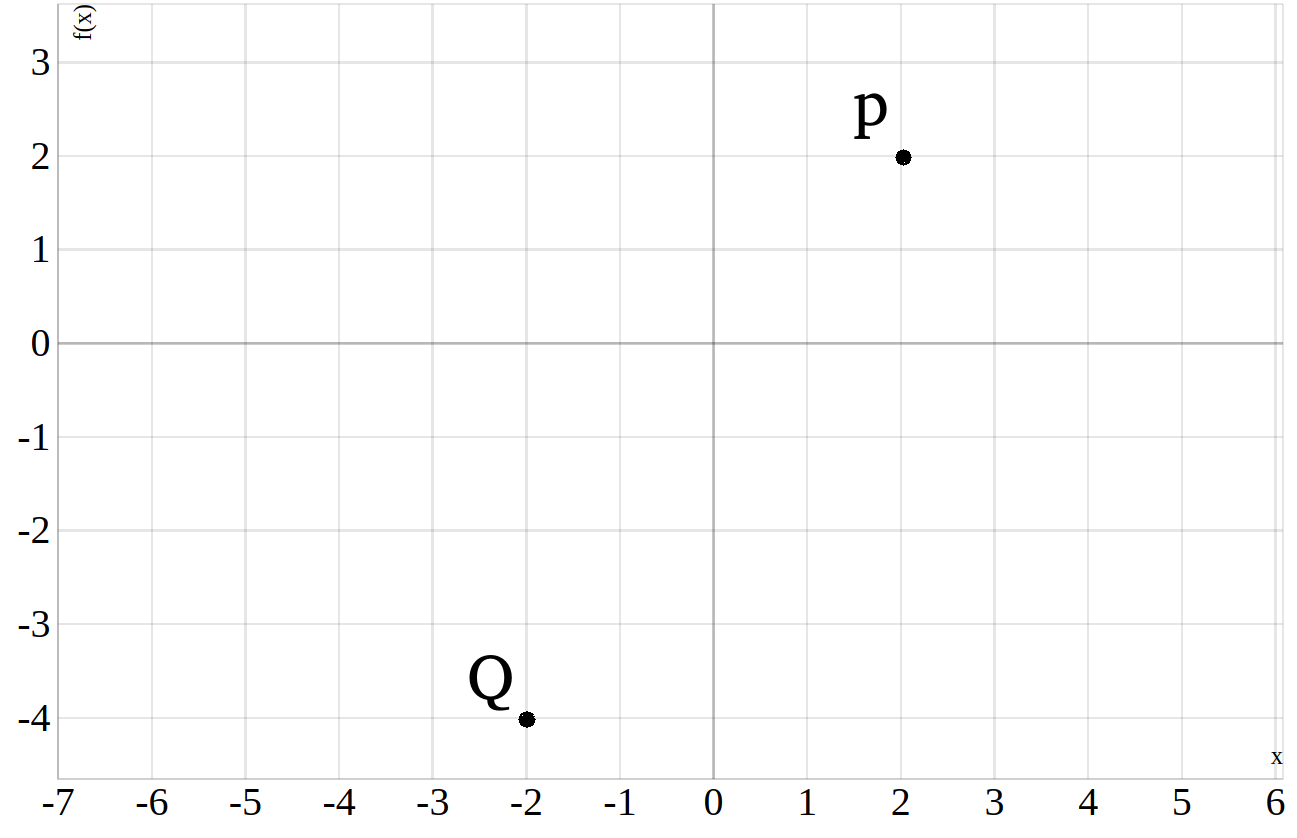
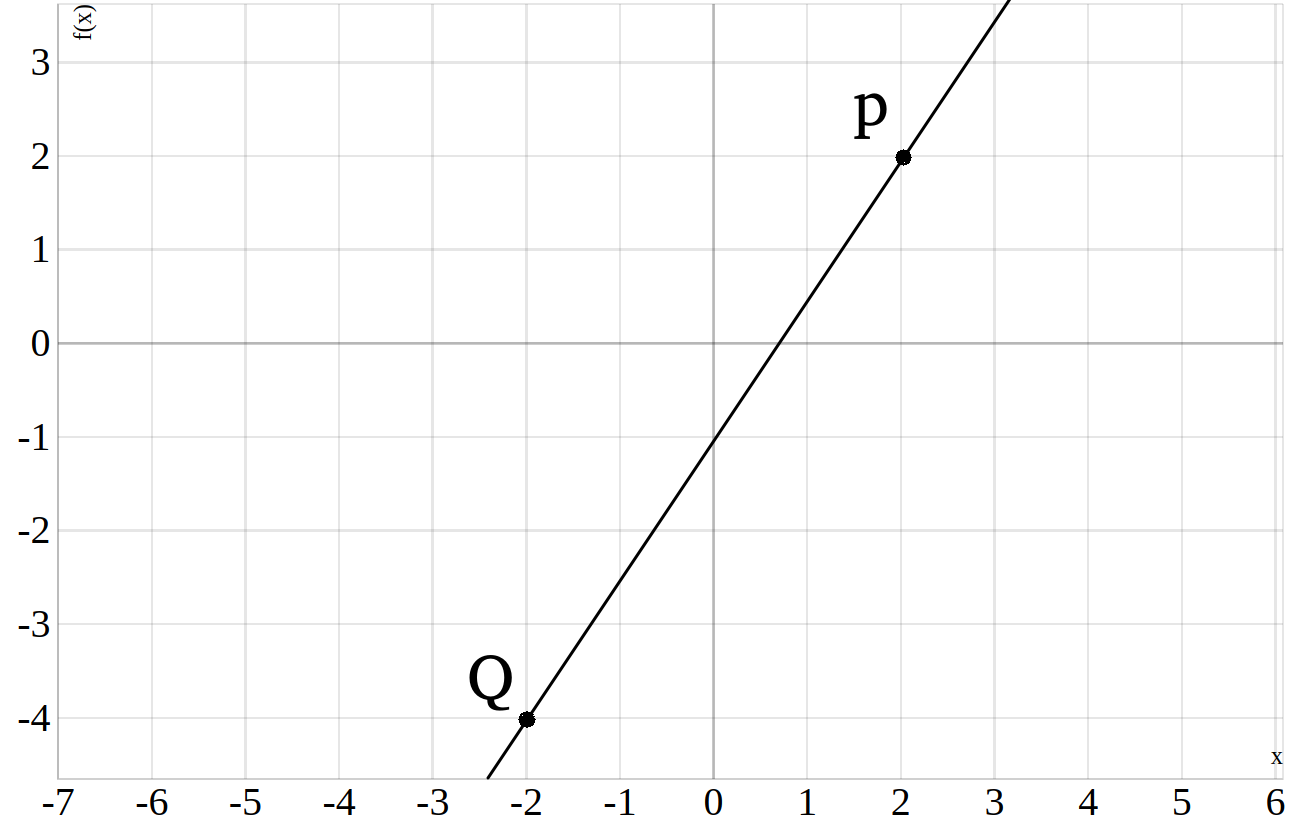
Um auf die Gerade zu kommen die durch beide Punkte \(Q\) und \(P\) geht, brauchen wir die allgemeine Geradengleichung
\(f(x)=m\cdot x+b\). Wir müssen also \(m\) und \(b\) ermitteln.
Steigungsformel
Um die Steigung einer linearen Funktion berechnen zu können, verwenden wir die Formel:
Gerade - Steigungsformel
\(\begin{aligned} m&=\frac{\Delta y}{\Delta x}\\ \\ m&=\frac{y_2-y_1}{x_2-x_1} \end{aligned}\)
Damit erhalten wir die Steigung über die Formel:
\(\begin{aligned} m=\frac{y_Q-y_P}{x_Q-x_P} \end{aligned}\)
Wobei \(y_Q\) die \(y\)-Koordinate des Punktes \(Q\) ist und \(y_P\) ist die \(y\)-Koordinate des Punktes \(p\). Das gleiche gilt natürlich im bezug auf \(x_Q\) und \(x_P\). Setzen wir mal unsere Werte in die Gleichung ein.
\(\begin{aligned} m=\frac{-4-2}{-2-2}=\frac{-6}{-4}=\frac{3}{2} \end{aligned}\)
Die Steigung der Geraden, welche durch die Punkte \(Q\) und \(P\) geht, ist \(m=\frac{3}{2}\).
Es ist übrigens Egal ob man
\(\begin{aligned} m=\frac{y_Q-y_P}{x_Q-x_P} \end{aligned}\)
oder
\(\begin{aligned} m=\frac{y_P-y_Q}{x_P-x_Q} \end{aligned}\)
berechnet. Es kommt das gleiche Ergebnis bei raus, probier es mal aus.
Lineare Funktion Steigung - Beispiele
Beispiel 1 - Steigung einer Lineare Funktion
Gegeben ist die Funktion
\(f(x)=3\cdot x -1\)
Bestimme die Steigung der linearen Funktion.
Lösung
\(f(x)=\textcolor{blue}{3}\cdot x -1\)
Die Steigung der linearen Funktion ist \(\textcolor{blue}{m}=\textcolor{blue}{3}\)
Beispiel 2 - Steigung aus zwei Punkten berechnen
Gegeben sind die Punkte \(Q=(0|1)\) und \(P=(4|3)\). Berechne die Steigung der linearen Funktion, welche durch diese zwei Punkte geht.
Lösung
Um die Steigung der Geraden, welche durch die zwei Punkte \(Q\) und \(P\) geht, nutzen wird die Steigungsformel
\(\begin{aligned} m&=\frac{y_P-y_Q}{x_P-x_Q}\\ \\ &=\frac{3-1}{4-0}=\frac{2}{4}=\frac{1}{2} \end{aligned}\)
Die Steigung der linearen Funktion welche durch die Punkte \(Q\) und \(P\) geht, beträgt \(m=\frac{1}{2}\).
