Lineare Funktion y Achsenabschnitt
Lineare Funktion Rechner
Der Online Rechner mit Rechenweg von Simplexy kannst du dir lineare Funktionen zeichnen lassen, Nullstellen berechnen, y-Achsenabschnitt berechnen und viel mehr.
Lineare Funktion y Achsenabschnitt
Eine Lineare Funktion hat ganz Allgemein die Form
\(f(x)=m\cdot x+b\)
Der Graph einer Linearen Funktion ist wie der Name schon sagt eine Gerade. Dabei nennt man \(m\) die Steigung der Geraden und \(b\) nennt man den \(y\)-Achsenabschnitt, also die Stelle an der die Gerade die \(y\)-Achse schneidet. In einem Koordinantensystem wird das aussehen der Geraden, durch die Werte \(m\) und \(b\) festgelegt.
Hier siehst du den Graphen der linearen Funktion \(f(x)=2\cdot x + 1\), wobei hier \(m=2\) und \(b=1\) ist:
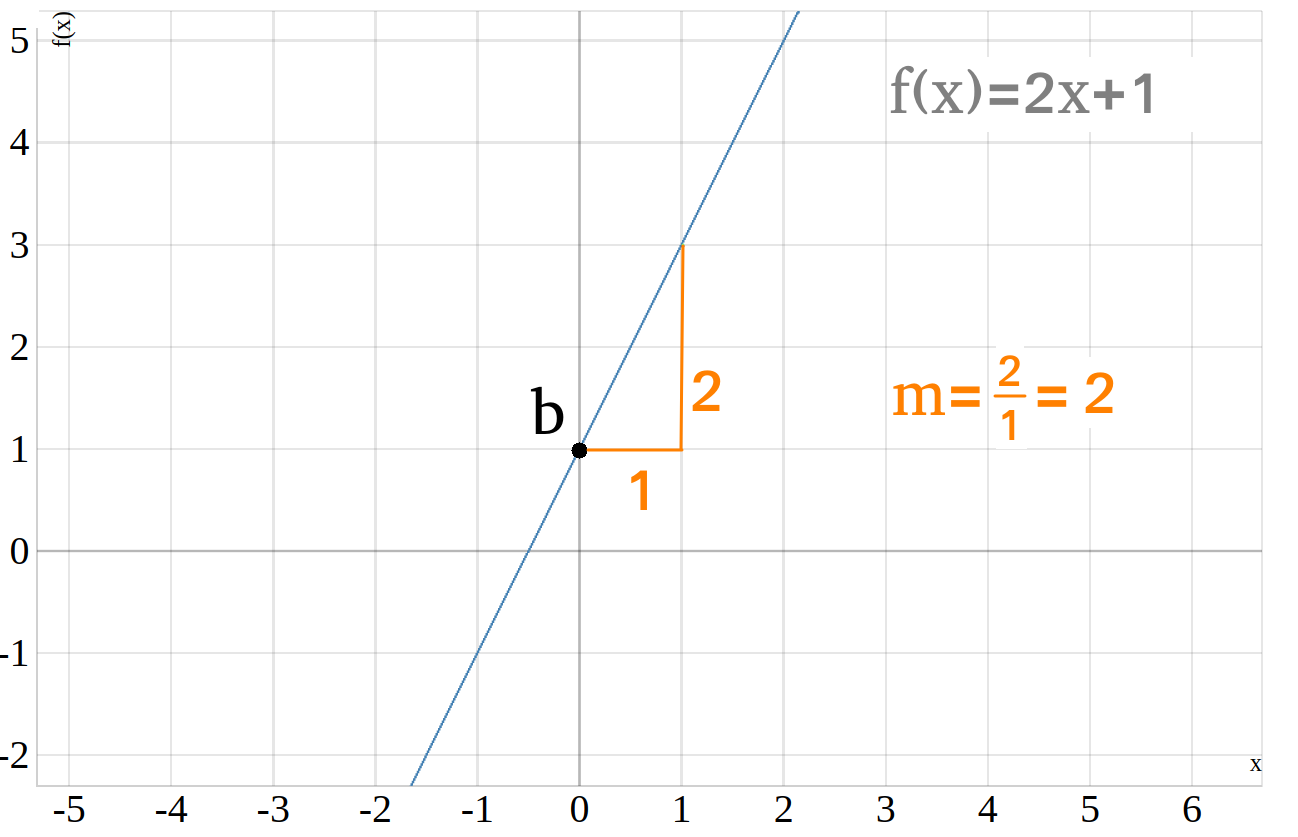
In dem obigen Graphen siehst du bereits wie man den y-Achsenabschnitt \(b\) bestimmen kann. Dazu muss du lediglich rausfinden an welcher Stelle die Gerade deine \(y\)-Achse schneidet. Hier in diesem Fall passiert das am Punkt \((0|1)\). In einem Koordinantensystem werden Punkte immer durch \((x|y)\) dargestellt. So findest du also raus, dass der \(y\)-Achsenabschnit am Punkt \((0|1)\) liegt und damit gilt \(b=1\).
Solche Graphen kannst du mit dem online Rechner für lineare Funktionen von Simplexy selber erstellen, gib in das Eingabefeld zum Beispiel
\(2\cdot x + 1\) ein und siehe was passiert. Hier kommst du zum Rechner für Geraden.
Negativer y Achsenabschnitt
Der \(y\)-Achsenabschnitt einer linearen Funktion kann auch negativ sein, das kannst du am zweiten Beispiel sehen.
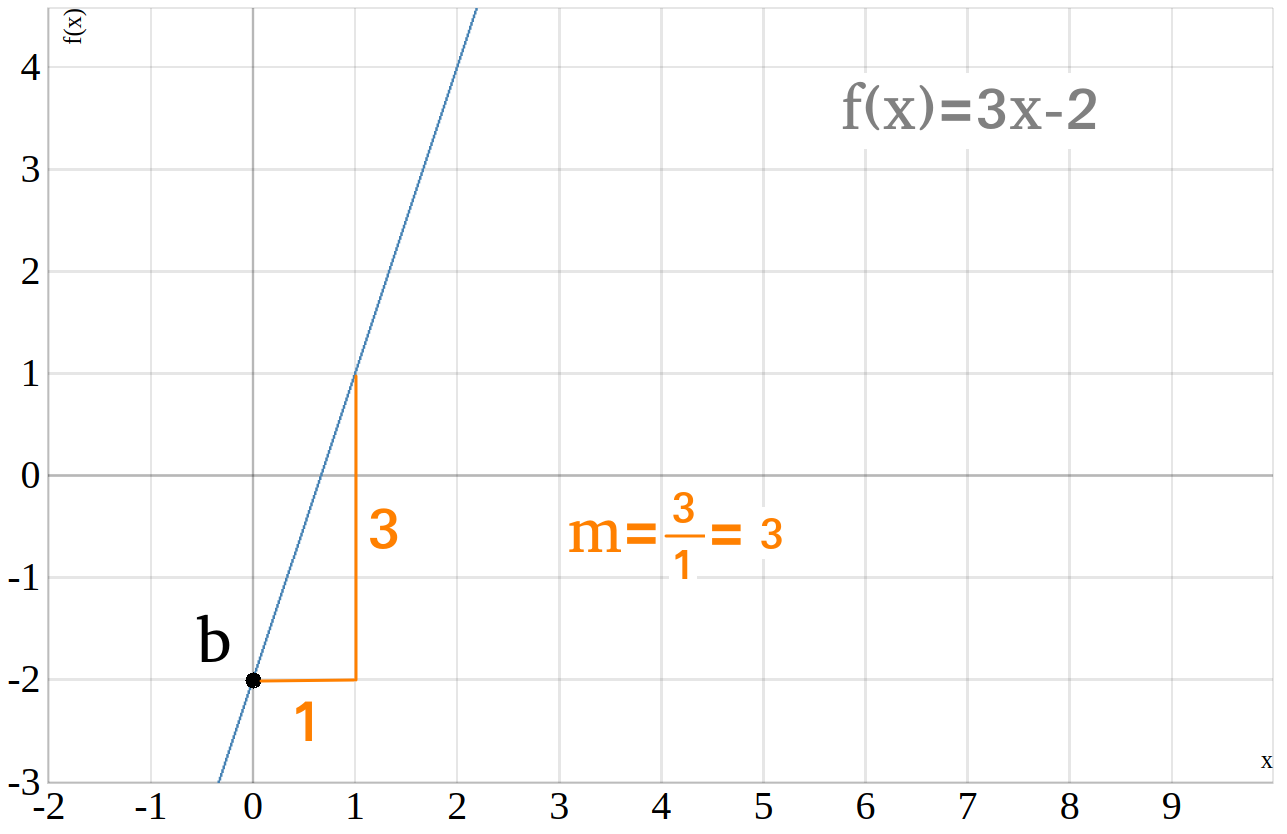
Wie du in dem Graphen oben siehst, lautet die Funktionsgleichung dieser Geraden
\(f(x)=3\cdot x - 2\)
Da die Gerade die \(y\)-Achse am punkt \((0|-2)\) schneidet, liegt der
y Achsenabschnitt der Funktion bei \(b=-2\).
Möchtest du zusätzlich noch die Steigung \(m\) der linearen Funktion berechnen? Dann werf einen Blick auf den Beitrag Steigung einer Linearen Funktion.
Lineare Funktion - y Achsenabschnitt
Der \(y\)-Achsenabschnitt ist der Punkt an dem die lineare funktion die \(y\)-Achse schneidet.
Man kann den \(y\)-Achsenabschnitt, also den Schnittpunkt der Funktion mit \(y\)-Achse, direkt aus der Funktionsgleichung ablesen. Eine Lineare Funktion hat stets die Form\(f(x)=m\cdot x+b\), der Wert \(b\) ist der \(y\)-Achsenabschnitt.
Konstante Funktion
Eine lineare Funktion kann auch parallel zur \(x\)-Achse verlaufen, so eine Gerade nennt man eine Konstante. Die Funktionsgleichung einer zur \(x\)-Achse parallelen Geraden lautet \(f(x)=b\), da die Steigung \(m=0\) ist, lässt sich die Funktion also nur durch den \(y\)-Achsenabschnitt ausdrucken.
Beispiel einer konstanten Funktion \(f(x)=3\)
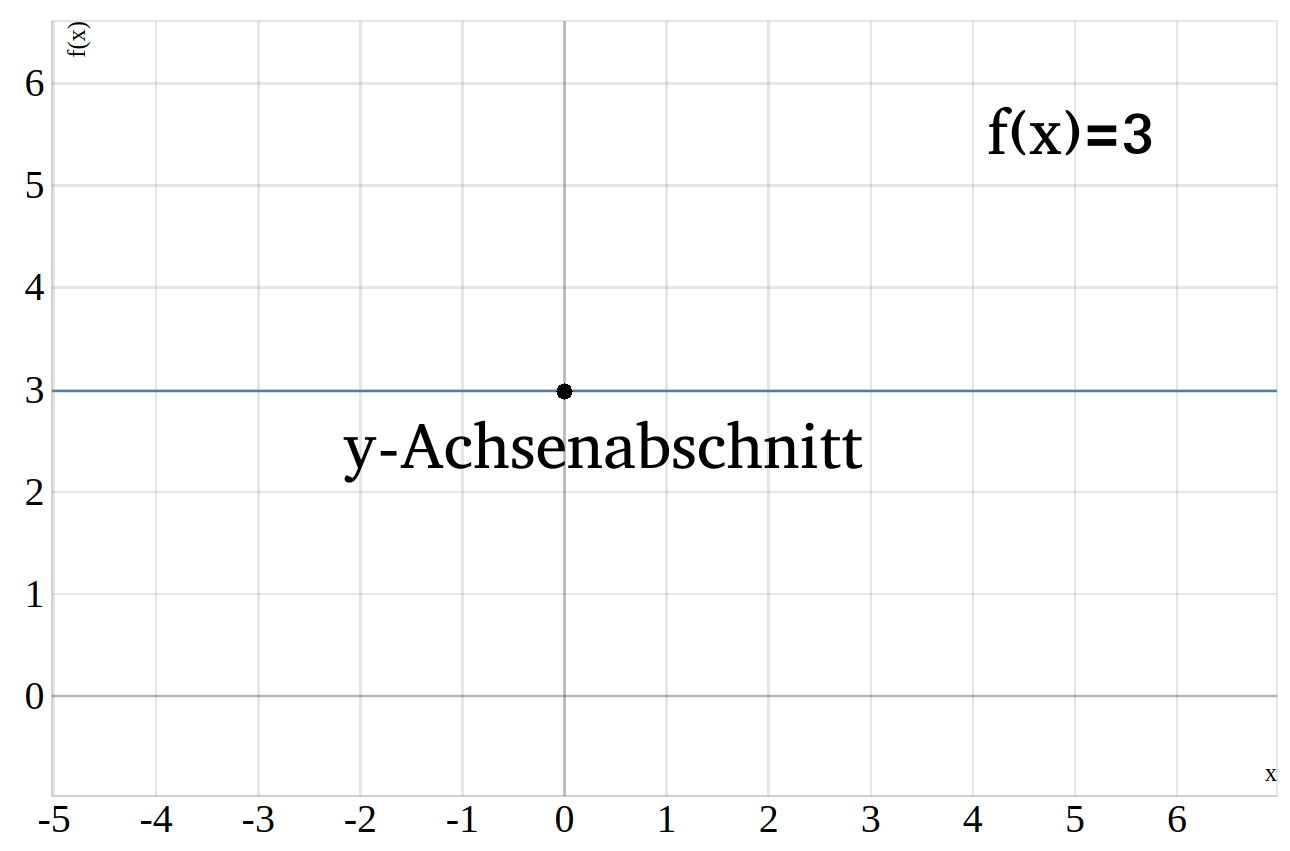
y Achsenabschnitt berechnen
Um den y Achsenabschnitt einer linearen Funktion berechnen zu können, muss man den Wert \(x=0\) in die Funktionsgleichung der linearen Funktion einsetzen.
Die allgemeine Form einer linearen Funktion lautet:
\(f(x)=m\cdot x +b\)
Da der y Achsenabschnitt beim Schnittpunkt der Funktion mit der y-Achse liegt, muss man den Wert \(x=0\) in die Funktionsgleichung einsetzen. Denn die y-Achse verläuft durch den Wert \(x=0\).
y Achsenabschnitt einer linearen Funktion
\(f(0)=m\cdot 0 + b=b\)
Beispiel y Achsenabschnitt berechnen
Gegeben ist die lineare Funktion
\(\begin{aligned} f(x)=-\frac{1}{2}\cdot x+3 \end{aligned}\)
Bestimme den y Achsenabschnitt.
Lösung
Um den y Achsenabschnitt der linearen Funktion berechnen zu können, setzt man den Wert \(x=0\) in die Funktionsgleichung:
\(\begin{aligned} f(0)=-\frac{1}{2}\cdot 0+3=3 \end{aligned}\)
Der y Achsenabschnitt liegt am Punkt \((0|3)\).
y Achsenabschnitt berechnen für zwei Punkte
Wie berechnet man den y Achsenabschnitt einer linearen Funktion, wenn lediglich zwei Punkte die auf der Gerade liegen, gegeben sind?
Wenn \(P_1=(x_1|y_1)\) und \(P_2=(x_2|y_2)\) zwei Punkte einer linearen Funktion \(f(x)=mx+b\) sind, so kann der y Achsenabschnitt der dazugehörigen geraden berechnet werden, indem zunächst die jeweiligen Punkte in die Funktionsgleichung eingesetzt werden.
\(\begin{aligned} y_1&=m\cdot x_1 + b \,\,\,\,(I)\\ \\ y_2&=m\cdot x_2 + b \,\,\,\,(II) \end{aligned}\)
Nun kann man sich eine der zwei Gleichungen aussuchen und nach \(m\) umstellen:
Wir machen das für die erste Gleichung \(I\) und erhalten:
\(\begin{aligned} m=\frac{y_1-b}{x_1} \end{aligned}\)
Diese Darstellung für \(m\) setzten wir nun in die zweite Gleichung \(II\) ein und erhalten:
\(\begin{aligned} y_2=\frac{y_1-b}{x_1}\cdot x_2+b \end{aligned}\)
Diese Gleichung müssen wir jetzt nach \(b\) umsellen und erhalten:
\(\begin{aligned} b=\frac{y_2\cdot x_1-y_1\cdot x_2}{x_1-x_2} \end{aligned}\)
Beispiel y Achsenabschnitt berechnen
Gegeben sind die zwei Punkte \(P_1=(1|3)\) und \(P_2=(2|4)\) einer linearen Funktion \(f(x)\). Wie lautet der y Achsenabschnitt dieser Funktion?
Um den y Achsenabschnitt der linearen Funktion berechnen zu können, verwenden wir die oben hergeleitete Formel
\(\begin{aligned} b=\frac{y_2\cdot x_1-y_1\cdot x_2}{x_1-x_2} \end{aligned}\)
Wir setzen nun die Werte \(x_1=1\), \(y_1=3\), \(x_2=2\) und \(y_2=4\) in die Formel ein und erhalten:
\(\begin{aligned} b&=\frac{4\cdot 1-3\cdot 2}{1-2}\\ \\ &=\frac{-2}{-1}=2 \end{aligned}\)
Der y Achsenabschnitt der linearen Funktion, welche durch die Punkte \(P_1\) und \(P_2\) geht, liegt bei \((0|2)\).
