Mitternachtsformel
Mitternachtsformel online Rechner
Mit dem Mitternachtsformel Rechner von Simplexy kannst du ganz simple die Nullstellen einer quadratischen Funktion berechnen, eine Parabel zeichnen lassen, die Mitternachtsformel online berechnen uvm.
Mitternachtsformel Erklärt
Die Mitternachtsformel oder auch ABC-Formel genannt wird angewandt, um die Nullstellen von quadratischen Funktionen zu berechnen. Mit der Mitternachtsformel kann man quadratische Gleichungen der folgenden Form lösen.
\(\textcolor{red}{a}x^2+\textcolor{blue}{b}x+\textcolor{green}{c}=0\)
Um so eine quadratische Gleichung lösen zu können, muss man die Zahlen welche an den Stellen a, b und c stehen, in die Mitternachtsformel einsetzen. Wie man die Mitternachtsformel anwenden kann um die Nullstellen von Parabeln berechnen zu können werden wir uns noch genauer ansehen.
Mitternachtsformel
\(\begin{aligned} x_{1/2}=\frac{-\textcolor{blue}{b}\pm\sqrt{\textcolor{blue}{b}^2-4\textcolor{red}{a}\textcolor{green}{c}}}{2\textcolor{red}{a}} \end{aligned}\)
Dabei ist
-
\(\textcolor{red}{a}\) die Zahl welche vor dem \(x^2\) steht.
-
\(\textcolor{blue}{b}\) die Zahl welche vor dem \(x\) steht.
-
\(\textcolor{green}{c}\) die Zahl welche alleine steht.
Wichtig ist hier, dass die Mitternachtsformel zwei Lösung liefert. Zum einen die Lösung \(x_1\) und zum anderen die Lösung \(x_2\). Dies liegt daran, dass quadratische Gleichungen bis zu zwei Lösung besitzen können. Wie wir bereits aus dem Beitrag Parabel Nullstellen berechnen wissen, können quadratische Funktion bis zu zwei Nullstellen bzw. Nullpunkte besitzen. Das sind die Schnittpunkte einer Parabel mit der x-Achse.
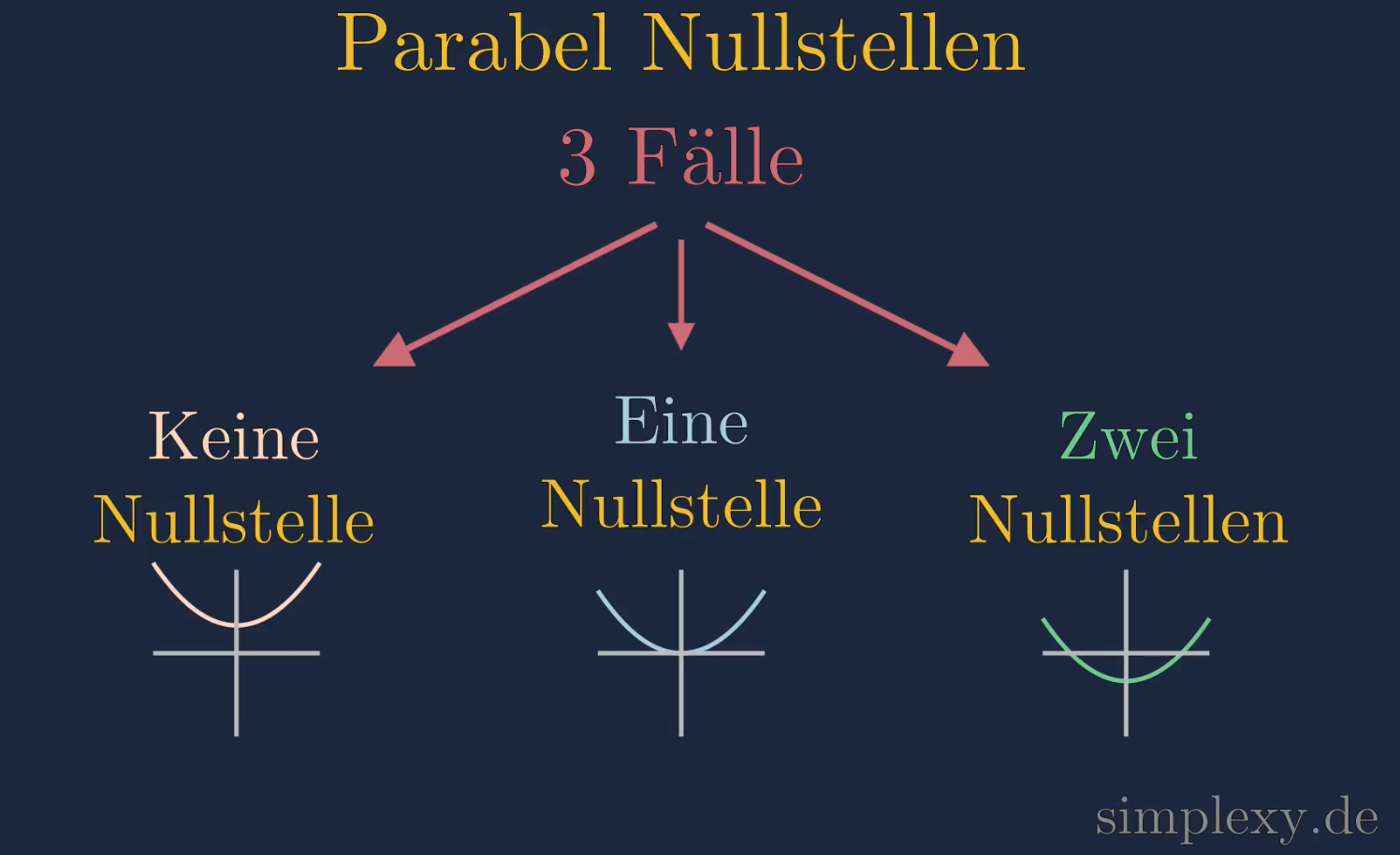
Mitternachtsformel plus und minus
Bei der Mitternachtsformel muss man zweimal rechnen. Einmal mit dem + vor der Wurzel und einmal mit dem - vor der Wurzel.
Mitternachtsformel Diskriminante
Der Term unter der Wurzel wird Diskriminante \(D\) genannt.
\(\begin{aligned} D=\textcolor{blue}{b}^2-4\textcolor{red}{a}\textcolor{green}{c} \end{aligned}\)
Steht unter der Wurzel eine negative Zahl (negative Diskriminante), so liefert die Mitternachtsformel keine Lösung.
Mitternachtsformel a b c bestimmten
Oft ist es nicht so einfach die Zahlen a, b und c bestimmen zu können.
Vor x^2 keine Zahl
Wie geht man vor, wenn vor dem \(x^2\) keine Zahl steht:
\(x^2+3x+8=0\)
In dem Fall steht vor dem \(x^2\) eine \(1\). Diese lässt man jedoch in der quadratischen Gleichung weg. Damit hat man für a, b und c die folgenden Werte:
\(\begin{aligned} a&=1\\ b&=3\\ c&=8 \end{aligned}\)
Vor x^2 ein minus
Steht vor dem \(x^2\) ein minus, wie in der folgenden Gleichung:
\(-x^2+4x+5=0\)
So hat man vor dem \(x^2\) eine \(-1\) zu stehen. Damit gilt:
\(\begin{aligned} a&=-1\\ b&=4\\ c&=5 \end{aligned}\)
Vor x ein minus
Steht vor dem x ein Minus, so steht dort eigentlich eine \(-1\).
\(2x^2-x+5=0\)
\(\begin{aligned} a&=2\\ b&=-1\\ c&=5 \end{aligned}\)
Keine Zahl ohne x
Steht keine Zahl alleine, wie in diesem Beispiel:
\(2x^2+5x=0\)
So gilt das \(c=0\) ist.
\(\begin{aligned} a&=2\\ b&=5\\ c&=0 \end{aligned}\)
Mitternachtsformel Parabel Nullstelle berechnen
Mit der Mitternachtsformel kann man die Nullstellen einer Parabel berechnen. Eine Parabel bzw. eine quadratische Funktion wird in der Normalform wie folgt dargestellt:
\(f(x)=ax^2+bx+c\)
Um die Nullstellen einer quadratischen Funktion berechnen zu können, muss man die Mitternachtsformel anwenden. Manchmal wird die Mitternachtsformel auch abc-Formel genannt.
Man erhält die Nullstellen einer Parabel indem man die Funktionsgleichung gleich Null setzt.
\(ax^2+bx+c=0\)
Damit hat man eine quadratische Gleichung, die man mit der Mitternachtsformel lösen kann.
Mitternachtsformel Nullstellen
\(\begin{aligned} x_{1/2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{aligned}\)
Fallunterscheidung
\(\begin{aligned} x_{1}=\frac{-b\textcolor{red}{-}\sqrt{b^2-4ac}}{2a} \end{aligned}\)
\(\begin{aligned} x_{2}=\frac{-b\textcolor{blue}{+}\sqrt{b^2-4ac}}{2a} \end{aligned}\)
Die Mitternachtsformel-Formel hat zwei Lösungen \(x_{1/2}\), denn eine quadratische Funktion kann bis zu zwei Nullstellen bestizen. Eine Parabel kann keine, eine oder zwei Nullstellen besitzen. Um die Anzahl an Nullstellen zu ermitteln, musst du die Diskriminante berechnen.
\(D=b^2-4ac\)
Die Diskriminante ist der Term unter der Wurzel in der Mitternachts-Formel. Es gilt:
Diskriminante
Über die Diskriminante erhält man die Anzahl an Nullstellen
- Wenn \(D < 0\) ist, dann existieren keine Nullstellen.
- Wenn \(D=0\) ist, dann existiert genau eine Nullstelle.
- Wenn \(D>0\) ist, dann existieren zwei Nullstellen.
Im unteren Bild sind die Graphen zweier Parabeln abgebildet, die blaue Parabel besitzt keine Nullstellen während die rote Parabel zwei Nullstellen besitzt.
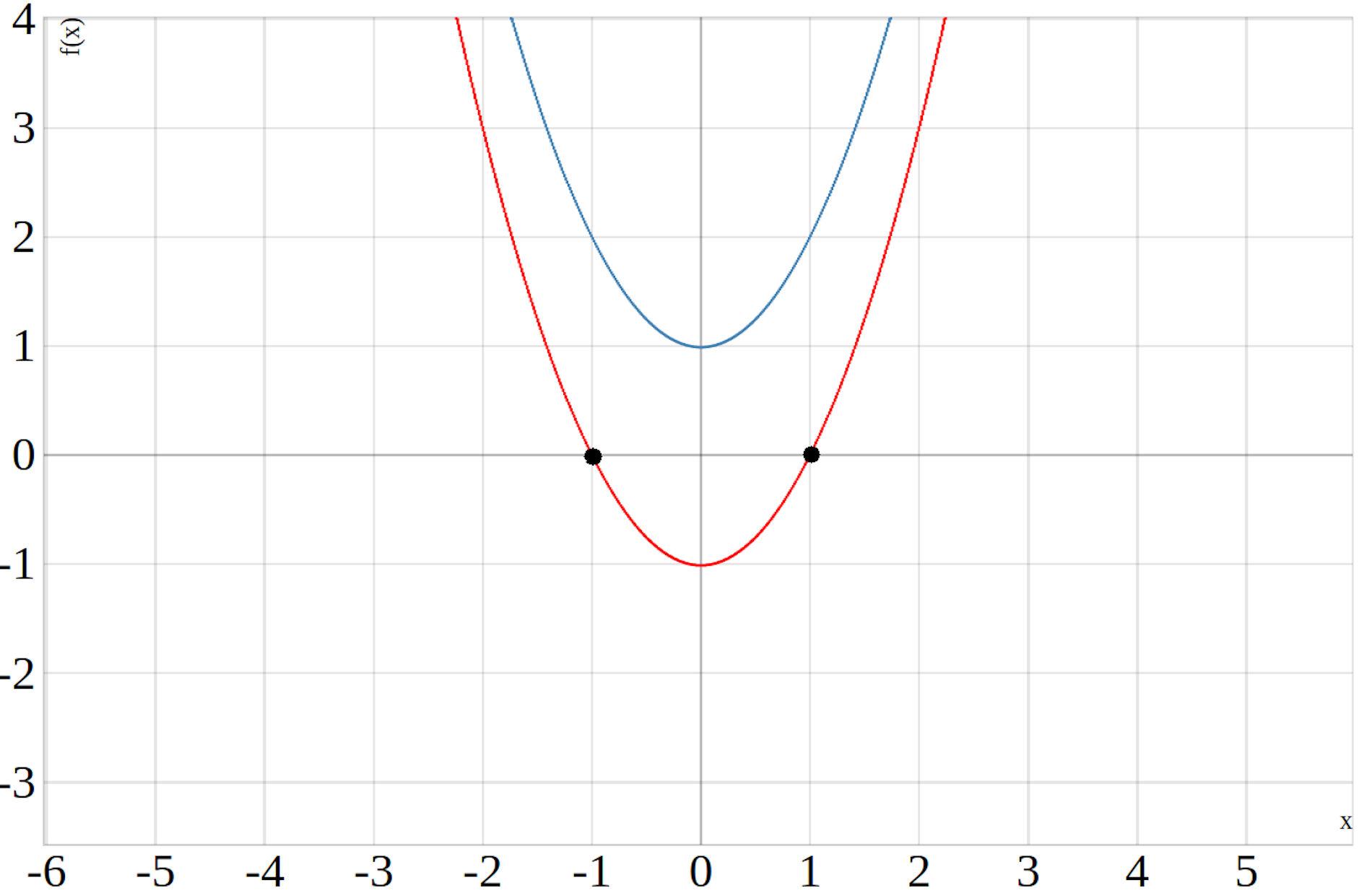
Parabel Nullstellen
Eine quadratische Funktion kann keine, eine oder zwei Nullstellen besitzen. Die Funktionsgleichung einer Parabel in der Normalform lautet:
\(f(x)=ax^2+bx+c\)
Die Nullstellen kann man mit der Mitternachtsformel berechnen.
\(\begin{aligned} x_{1/2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{aligned}\)
Nullstellen von Parabeln berechnen
Vorgehen
Quadratische Funktion in die Normalform bringen.
\(a,b\) und \(c\) aus der Normalform ablesen.
\(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
Mitternachtsformel ausrechnen.
Mitternachtsformel anwenden
Um die Anwendung der Mitternachtsformel üben zu können werden wir nun einige Beispiele betrachten.
Beispiel 1
\(f(x)=2x^2-12x-14\)
Die Funktion ist bereits in der Normalform angegeben. Wir gehen sofort zum zweiten Schritt über. Die werte \(a,b\) und \(c\) können wir ablesen.
\(a=2,\) \(b=-12\) und \(c=-14\)
Diese Werte setzen wir in die Mitternachtsformel ein.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-(-12)\pm\sqrt{(-12)^2-4\cdot 2\cdot (-14)}}{2\cdot 2}\\ \\ &=\frac{12\pm\sqrt{144+112}}{4}\\ \\ &=\frac{12\pm\sqrt{256}}{4}\\ \\ &=\frac{12\pm 16}{4}\\ \end{aligned}\)
Fallunterscheidung:
\(x_{1}=\)\(\frac{12-16}{4}\)\(=-1\)
\(x_{2}=\)\(\frac{12+16}{4}\)\(=7\)
Die Nullstellen der Parabel befinden sich somit bei
\(x_1=-1\) und \(x_2=7\).
Beispiel 2
\(f(x)=4x^2-16x+16\)
Die Funktionsgleichung befindet sich schon in der Normalform. Wir können damit direkt zum zweiten Schritt springen. Wir müssen also \(a,b\) und \(c\) ablesen.
\(a=4,\) \(b=-16\) und \(c=16\)
Nun können wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-(-16)\pm\sqrt{(-16)^2-4\cdot 4\cdot 16}}{2\cdot 4}\\ \\ &=\frac{16\pm\sqrt{256-256}}{8}\\ \\ &=\frac{16\pm\textcolor{blue}{\sqrt{0}}}{8}\\ \\ &=\frac{16\pm 0}{8}\\ \\ &=\frac{16}{8}\\ \\ &=2\\ \end{aligned}\)
In diesem Beispiel hat die Parabel nur eine Nullstelle, da
die Diskriminante \(D\) gleich Null ist.
\(D=b^2-4ac=0\)
Die einzige Nullstelle befindet sich bei \(x_0=2\).
Beispiel 3
\(f(x)=2x^2-8x+11\)
Die Funktion befindet sich bereits in der Normalform. Wir können also direkt zum zweiten Schritt übergehen und \(a,b\) und \(c\) ablesen.
\(a=2,\) \(b=-8\) und \(c=11\)
Nun müssen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ &=\frac{-(-8)\pm\sqrt{(-8)^2-4\cdot 2\cdot 11}}{2\cdot 2}\\ &=\frac{8\pm\sqrt{64-88}}{4}\\ &=\frac{16\pm\textcolor{red}{\sqrt{-24}}}{4}\\ \end{aligned}\)
Die Parabel hat also keine Nullstelle. In den reellen Zahlen ist die Wurzel einer negativen Zahl nicht definiert. Aus diesem Grund hat die Parabel keine Nullstellen. Sie befindet sich vollständig oberhalb der \(x-\)Achse.
Nutze den Mitternachtsformel-Rechner von Simplexy kannst du Nullstellen einer quadratischer Funktionen berechnen. Gib dazu am besten zur Probe mal \(x^2+2x-5=0\) ein, du erhältst die Nullstellen und den Rechenweg.
Hier kommst du zum Rechner.
