Die Normalparabel
Parabel Rechner
Mit dem Parabelrechner von Simplexy kannst du ganz einfach die Nullstellen einer quadratischen Funktion berechnen, eine Normalparabel zeichnen uvm.
Normalparabel
Die Normalparabel hat die Form
\(f(x)=x^2\)
Die Normalform bzw. allgemeine Form einer Parabel wird mathematisch folgendermaßen dargestellt
\(f(x)=ax^2+bx+c\)
Demzufolge sind bei der Normalparabel die Parameter \(b\) und \(c\) aus der allgemeinen Form einer quadratischen Funktion gleich Null und der Parameter \(a=1\). Der Scheitelpunkt einer Normalparabel befindet sich am Punkt \((0,0)\) und die Nullstelle liegt bei \(x_{0}=0\). Der Graph der Normalparabel ist unten dargestellt.
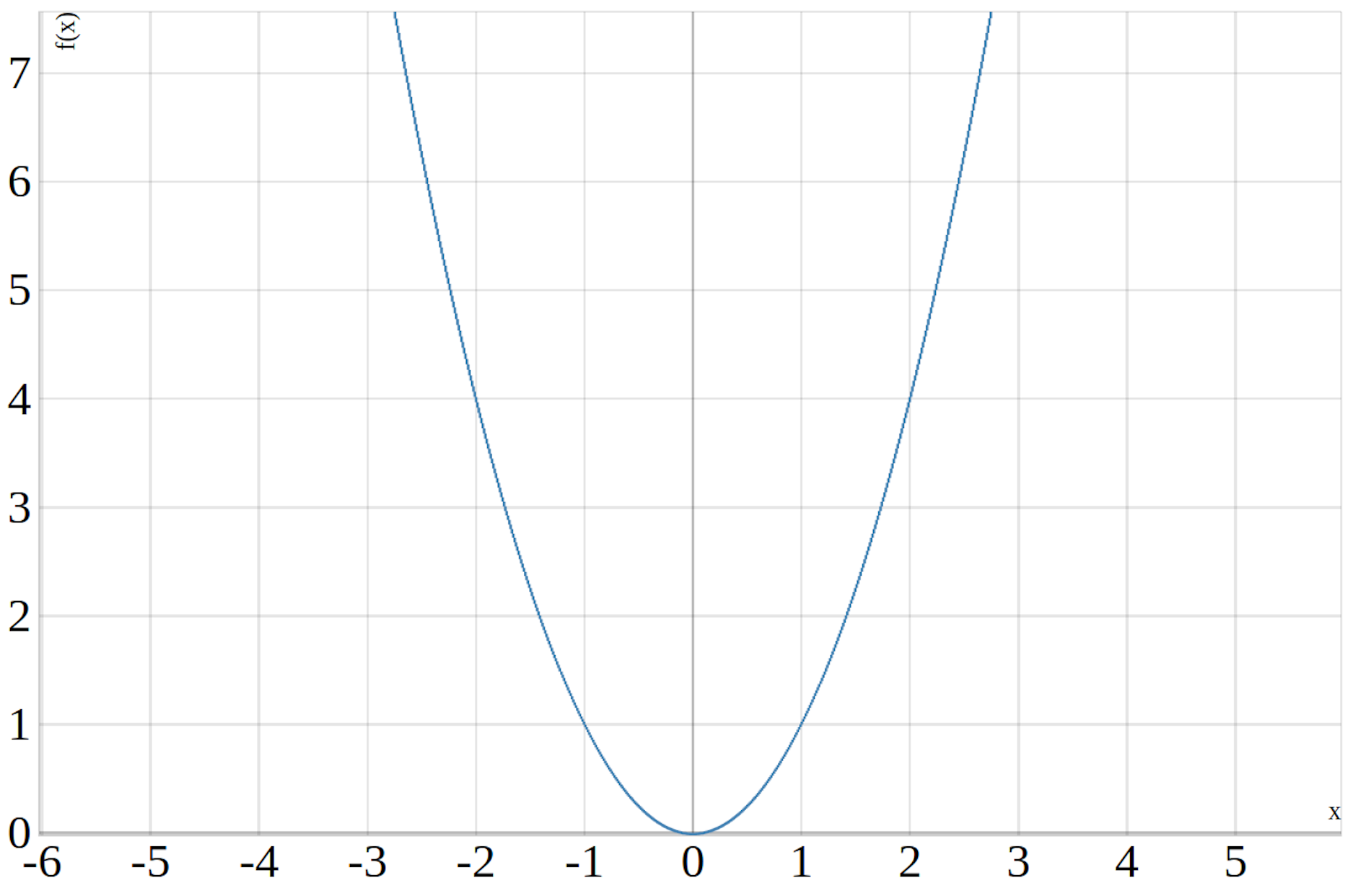
Die Normalparabel ist die einfachste Art einer Parabel bzw. einer quadratischen Funktion.
Wenn du mehr über Parabeln und quadratische Funktionen lernen möchtest, dann wirf einen Blick auf den Beitrag quadratische Funktionen und Parabeln
Quadratische Funktion und Parabel
Der Graph einer quadratischen Funktion wird Parabel genannt. Das Aussehen einer Parabel hängt von der Funktionsgleichung ab. Eine Parabel kann beispielsweise nach oben oder nach unten geöffnet sein. Jede Parabel ist symmetrisch, dabei verläuft die Symmetrieachse parallel zur \(y\)-Achse. Als Scheitelpunkt wird der Schnittpunkt der Parabel mit ihrer Symmetrieachse genannt. Des Weiteren kann eine Parabel Schnittpunkte mit der x-Achse besitzen, diese Schnittpunkte werden Nullstellen genannt. Dabei kann eine Parabel bis zu zwei Nullstellen besitzen. Liegt der Scheitelpunkt der Parabel über der x-Achse, so besitzt sie keine Nullstellen.
Du möchtest mehr über die Nullstellen von Parabeln und über den Scheitelpunkt einer Parabel lernen? Dann klicke auf die jeweiligen Links...
Beispiele für Parabeln
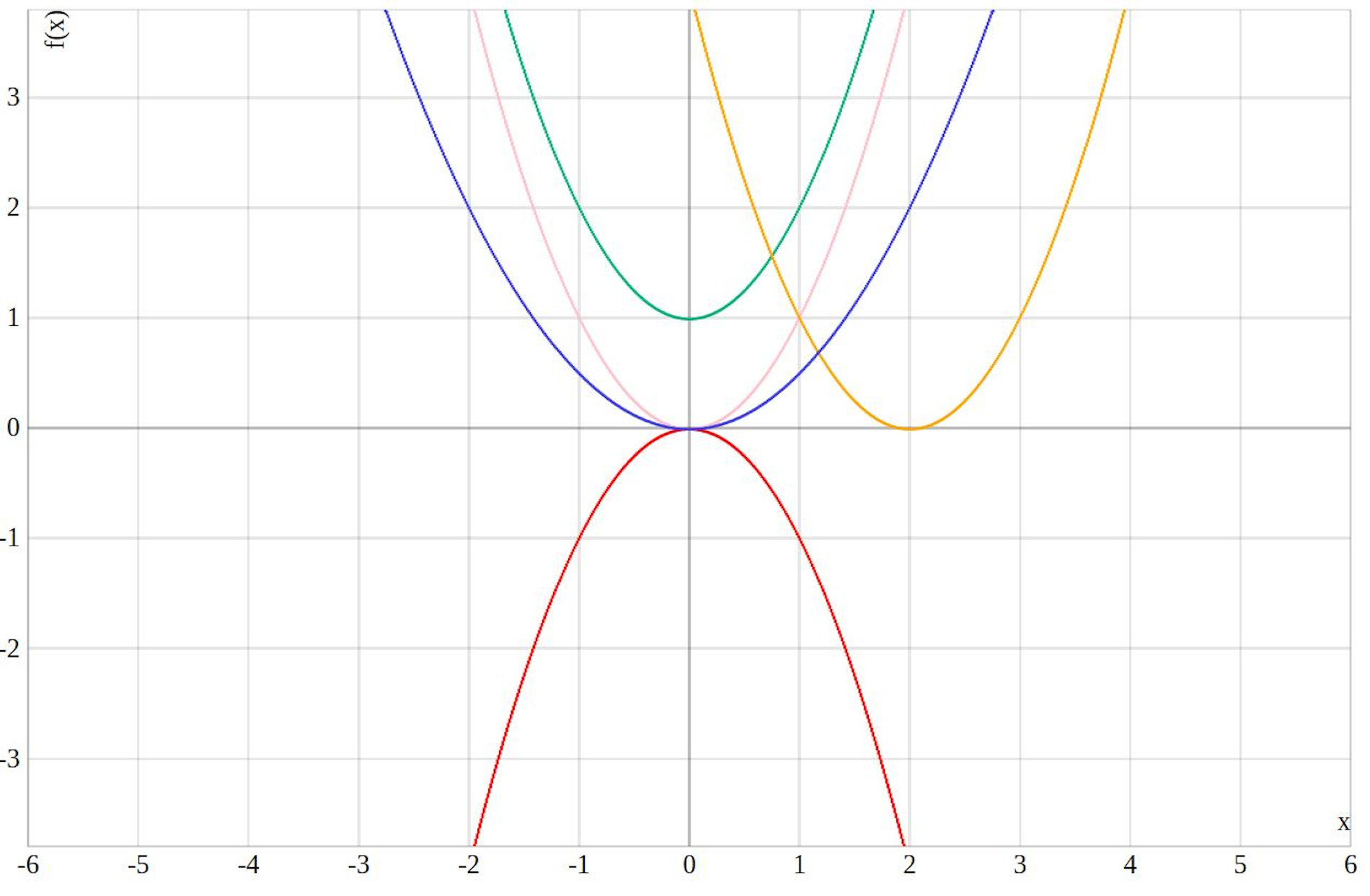
Solche Graphen kannst du mit dem Schritt für Schritt Rechner von Simplexy selber erstellen, gib eine beliebige Parabel bzw. quadratische Funktion in das Eingabefeld ein und siehe was passiert. Simplexy besitzt auch ein Nullstellen Rechner und ein qp-Formel Rechner mit Rechenweg. Gib dazu am besten zur Probe mal \(x^2+2x-5=0\) ein, du erhältst die Nullstellen und den Rechenweg.
Hier kommst du zum Rechner.
Normalform einer Parabel
Die allgemeine Form oder auch Normalform einer quadratischen Funktion lautet:
\(f(x)=ax^2+bx+c\)
Die Normalparabel besitzt die Funktionsgleichung:
\(f(x)=x^2\)
Normalparabel Wertetabelle
Du möchtest wissen wie man die Wertetabelle der Normalparabel erstellt?
Dann guck dir das Video dazu an.
Normalparabel Zeichnen
Du möchtest wissen wie man eine Normalparabel zeichnen kann?
Dann guck dir das Video dazu an.
