Nullstellen berechner
Nullstellen berechner
Mit dem Nullstellen berechner von Simplexy kannst du ganz einfach die Nullstellen verschiedener Funktionen berechnen, den Rechenweg anzeigen, die Funktionen zeichnen lassen und viel mehr. Möchtest du zum Beispiel die Nullstelle einer Parabel berechnen, so kannst du in das Eingabefeld \(x^2=0\) eingeben und dann auf Lösen clicken. Wenn du möchtest kannst du dann auf Rechenweg anzeigen clicken und dir den Rechenweg anzeigen lassen.
Linearen Funktion Nullstelle
Was ist eine Nullstelle ?
Die Nullstelle einer Linearen Funktion oder jeder anderen Funktion ist der Punkt im Koordinatensystem, an dem die Funktion die \(x\)-Achse berührt oder schneidet. Um den Punkt zu berechnen, an dem eine Funktion die \(x\)-Ache berührt, muss man also die Funktionsgleichung Null-Setzen. Denn die Nullstelle ist ja, der Punkt an dem die Funktion den Wert \(f(x)=0\) oder in einer anderen Schreibweise \(y=0\) besitzt.
In manchen Fällen verwendet man die Schreibweise
\(f(x)=...\)
und in anderen Fällen begegnet man die Schreibweise
\(y=...\)
Beide Schreibweisen sind identisch. Sowohl die Schreibweise \(f(x)\) als auch die Schreibweise \(y\) werden verwendet um eine Funktion anzugeben.
Beispiel
In diesem Beispiel möchten wir die Nullstelle der Funktion \(f(x)=2\cdot x -3\) berechnen. Der Graph der Funktion ist unten abgebildet.
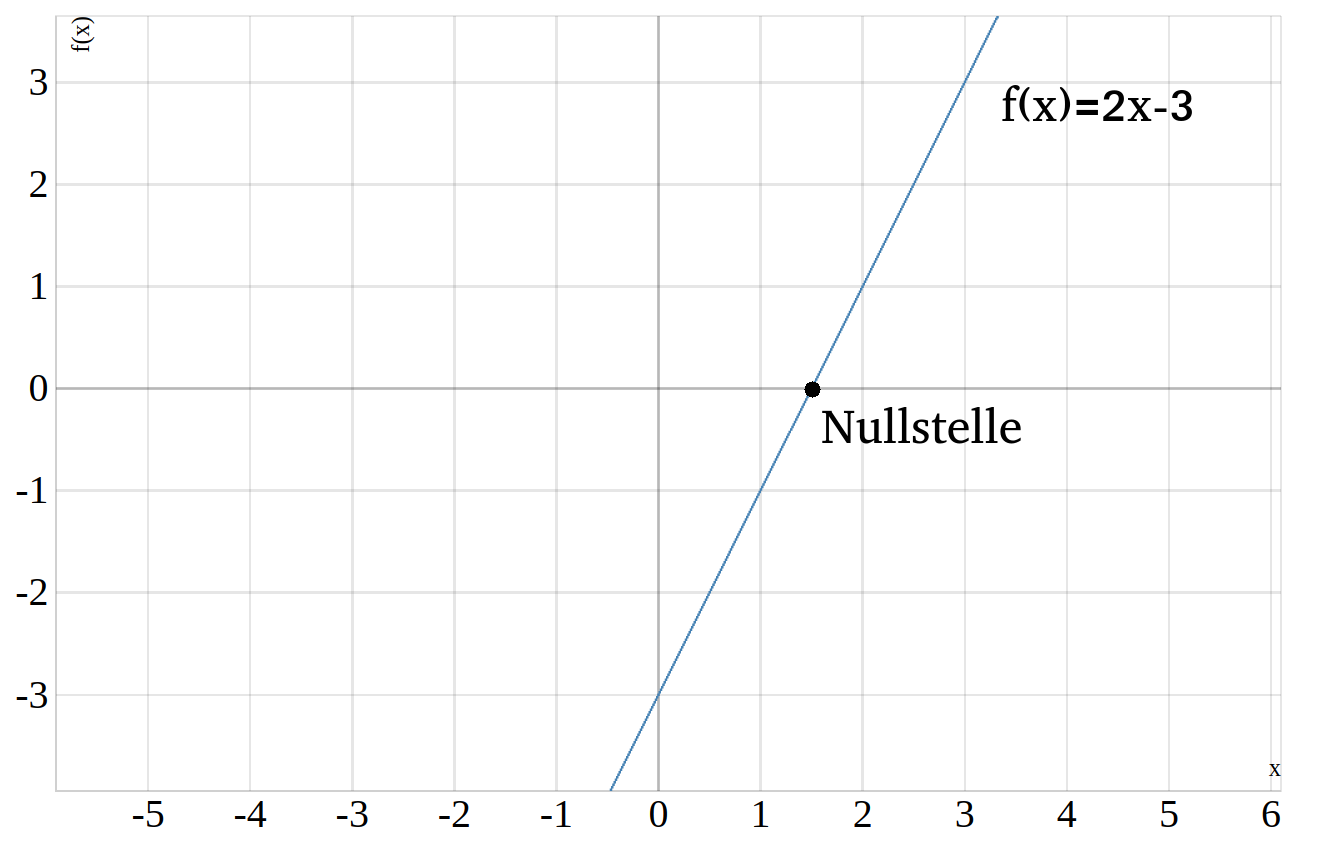
Um die Nullstelle zu berechnen müssen wir die Funktionsgleichung Nullstetzen, dazu schrieben wir:
\(0=2\cdot x -3\)
Damit haben wir eine lineare Gleichung, die wir nach \(x\) umstellen bzw. auflösen müssen. Benötigst du Hilfe bei dem Umstellen einer Funtkion, so kannst du hier clicken.
\(\begin{aligned} 0&=2\cdot x -3\,\,\,\,\,|+3\\ \\ 3&=2\cdot x\\ \\ 3&=2\cdot x\,\,\,\,\,|:2\\ \\ \frac{3}{2}&=x \end{aligned}\)
Wir haben also als Nullstelle \(x=\)\(\frac{3}{2}\)\(=1,5\) ermittelt, im Graphen kann man das überprüfen.
Regel:
Die Nullstelle einer linearen Funktion berechnet man, indem man die Geradengleichung \(f(x)=m\cdot x+b\) Nullsetzt.
Dann muss man \(0=m\cdot x+b\) nach \(x\) umstellen.
Allgemein geschrieben ist die Nullstelle gegeben durch die Formel \(x=-\frac{b}{m}\).
Im unteren Video ist ein weitere Beispiel zum berechnen einer Nullstelle dargestellt.
Solche Nullstellen kannst du mit dem Nullstellen berechner von Simplexy ermitteln. Der Rechner gibt dir die Lösung, einen Graphen und den Rechenweg an. Um die Nullstelle der Funktion \(f(x)=2\cdot x - 3\) zu bestimmt musst du im Eingabefeld \(2\cdot x -3 = 0\) eingeben, den rest erledigt der Rechner. So kannst du immer überprüfen ob du richtig gerechnet hast.
Nullstellen einer quadratischen Funktion
Parabeln kommen in vier Formen vor
\(f(x)=ax^2\)
\(f(x)=ax^2+c\)
\(f(x)=ax^2+bx\)
\(f(x)=ax^2+bc+c\)
Um die Nullstelle einer quadratische Funktionen (Parabel) zu berechnen kommen daher vier Fälle zustande. Ebenso wie bei den Linearen Funktionen berechnet man die Nullstelle einer quadratischen Funktion, indem man die Funktionsgleichung Nullsetzt. Denn die Nullstelle einer quadratischen Funktion ist stets beim \(y-\)Wert \(y=0\). In einigen Fällen benutzt man statt \(y\) auch die Schreibweise \(f(x)\), die zwei Schreibweisen bedeuten das gleiche.
\(y=f(x)\)
1. Fall
\(f(x)=ax^2\)
In dem ersten Fall besitzt eine Parabel nur eine Nullstelle.
Beispiele
\(f(x)=x^2\)
\(f(x)=2x^2\)
\(f(x)=-3x^2\)
\(f(x)=\frac{1}{2}x^2\)
\(f(x)=-\frac{3}{4}x^2\)
Hier ist die Nullstelle stets bei \(x_0=0\). Der \(y-\)Wert ist selbstverständlich ebenfalls bei \(y=0\). Die Koordinaten jedes Punktes werden angegeben über den \(x\)-Wert und den dazugehörigen \(y\)-Wert, dass ist bei den Koordinaten der Nullstelle genauso:
\(x_0=\{0,0\}\)
2. Fall
\(f(x)=ax^2+c\)
Hier bekommt man die Nullstelle, indem man die Funktionsgleichung wieder Nullsetzt und dann nach \(x^2\) umstellt. Im Anschluss muss man die Wurzel ziehen um den \(x\)-Wert der Nullstelle zu ermitteln.
Beispiel 1
\(f(x)=x^2-4\)
Zunächst müssen wir die Funktionsgleichung Nullsetzen:
\(0=x^2-4\)
Anschließend müssen wir die Gleichung nach \(x\) umstellen:
\(\begin{aligned} 0&=x^2-4\,\,\,\,|+4\\ 4&=x^2\,\,\,\,\,\,\,\,\,\,\,\,\,\,|\sqrt{\hspace{1em}}\\ \sqrt{4}&=\sqrt{x^2}\\ \sqrt{4}&=x\\ \end{aligned}\)
zuletzt muss man noch wissen, das die Wurzel von Vier zwei lösungen besitzt. Es gilt:
\(\sqrt{4}=2\) und \(\sqrt{4}=-2\)
Damit hat man also
\(2=x\)
und
\(-2=x\)
Es existieren also zwei Nullstellen, die eine liegt bei \(x_1=2\) und die andere bei \(x_2=-2\).
Einige Funktionen besitzen mehr als nur eine Nullstelle. Bei linearen Funktion existiert nur eine Nullstelle während quadratische Funktionen bis zu zwei Nullstellen besitzen können. Es kann auch vorkommen, das eine Funktion gar keine Nullstellen besitzt oder unendliche viele Nullstellen besitzt.
Mit dem Nullstellen berechner kann man sich eine Funktion zeichnen lassen und so eine Vorstellung über die Funktion bekommen.
Beispiel 2
Bestimme die Nullstelle der folgenden Funktion.
\(f(x)=x^2+8\)
Als Erstes müssen wir die Funktionsgleichung wieder Nullsetzen:
\(0=x^2+8\)
Nun können wir die Gleichung nach \(x^2\) umstellen und die Wurzel ziehen:
\(\begin{aligned} 0&=x^2+8\,\,\,\,|-8\\ -8&=x^2\,\,\,\,\,\,\,\,\,\,\,\,\,\,|\sqrt{\hspace{1em}}\\ \sqrt{-8}&=\sqrt{x^2}\\ \sqrt{-8}&=x\\ \end{aligned}\)
Hier müssen wir als die Wurzel von \(-8\) berechnen. Die Wurzel einer negativen Zahl ist jedoch (in den Reellen Zahlen \(\mathbb{R}\)) nicht definiert!
Wir können also nicht weiter rechnen und brechen die Rechnung an der Stelle ab. Unsere Funktion besitzt keine Nullstellen. Das bedeutet, dass diese Parabel vollständig oberhalb der \(x\)-Achse verläuft. Mit dem Nullstellen berechner kann man sich ein Bild von der Funktion machen lassen.
3. Fall
Berechne die Nullstelle der folgenden Funktion.
\(f(x)=ax^2+bx\)
Um die Nullstelle einer solchen Funktion zu berechnen, müssen wir die Funktionsgleichung wieder Nullsetzen und dann nach \(x\) umstellen.
Beispiel 1
Berechne die Nullstelle der folgenden Funktion.
\(f(x)=x^2+8x\)
Wir müssen als erstes wieder die Funktion Nullsetzen:
\(0=x^2+8x\)
Bevor wie die Gleichung nach \(x\) umstellen, werden wir das \(x\) in der Gleichung ausklammern. Diesen Trick kann man bei Funktionen dieser Form immer anwenden. Das Ausklammern von \(x\) ermöglicht es uns den Satz vom Nullprodukt anzuwenden.
\(0=x\cdot(x+8)\)
Nun können wir den Satz vom Nullprodukt nutzen um die Nullstellen der Parabel zu ermitteln. Wir teilen die Gleichung in zwei Faktoren:
\(0=\underbrace{x}_{1. Faktor}\cdot(\underbrace{x+8}_{2. Faktor})\)
Der Satz vom Nullprodukt besagt: "Ein Produkt ist genau dann Null, wenn einer der Faktoren gleich Null ist".
Wir Können also beide Faktoren getrennt gleich Null setzen und erhalten so zwei getrennte Gleichungen.
1 Faktor:
\(\begin{aligned} x&=0\\ \implies&\\ x_1&=0 \end{aligned}\)
Die erste Nullstelle befindet sich also beim \(x-\)Wert \(x_1=0\).
2 Faktor:
\(\begin{aligned} x+8&=0\\ x+8&=0\,\,\,\,\,\,\,\,\,\,|-8\\ x&=-8\\ \\ \\ \implies x_2&=-8 \end{aligned}\)
Die zweite Nullstelle befindet sich somit beim \(x-\)Wert \(x_2=-8\).
Diese quadratische Funtkion besitzt also zwei Nullstellen mit den Koordinaten:
\(\begin{aligned} x_1&=\{0,0\}\\ &\text{und}\\ x_2&=\{-8,0\}\\ \end{aligned}\)
Der Nullstellen berechner von Simplexy kann auch mehrere Nullstellen berechnen.
Beispiel 2
Berechne die Nullstelle der Funktion
\(f(x)=2x^2-4x\)
Als erstes setzen wir die Funktionsgleichung wieder Null:
\(0=2x^2-4x\)
Nun können wir wieder \(x\) ausklammern und den Satz vom Nullprodukt anwenden:
\(0=x\cdot(2x-4)\)
Wir teilen die Gleichung wieder in zwei Faktoren:
\(\underbrace{x}_{1. Faktor}\cdot(\underbrace{2x-4}_{2. Faktor})=0\)
Wir können jetzt wieder den Satz vom Nullprodukt anwenden. Wir setzen also beide Faktoren erneut gleich Null setzen.
1 Faktor:
\(\begin{aligned} x&=0\\ \implies&\\ x_1&=0 \end{aligned}\)
Die erste Nullstelle befindet sich somit beim \(x-\)Wert:
\(x_1=0\)
2 Faktor:
\(\begin{aligned} 2x-4&=0\\ 2x-4&=0\,\,\,\,\,\,\,\,\,\,|+4\\ 2x&=4\,\,\,\,\,\,\,\,\,\,|\div 2\\ x&=2\\ \\ \implies x_2&=2 \end{aligned}\)
Die zweite Nullstelle befindet sich somit beim \(x-\)Wert \(x_2=2\).
Wir haben als wieder eine Funktion mit zwei Nullstellen:
\(\begin{aligned} x_1&=\{0,0\}\\ &\text{und}\\ x_2&=\{2,0\}\\ \end{aligned}\)
Mit dem Nullstellen berechner kann man auch die Nullstellen von Funktionen mit zwei Nullstellen berechnen.
4. Fall
\(f(x)=ax^2+bx+c\)
Der letzte Fall ist der schwierigste Fall. Man benötigt hier die Mitternachtsformel bzw. die pq-Formel um die Nullstellen zu berechnen.
Wie in den anderen Fällen auch, berechnet man die Nullstellen indem man die Funktionsgleichung Nullsetzt.
\(ax^2+bx+c=0\)
Die Gleichung kann man mit Hilfe der Mitternachtsformel Lösen.
Mitternachtsformel
\(x_{1/2}=\)\(\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
Fallunterscheidung:
\(x_{1}=\)\(\frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(x_{2}=\)\(\frac{-b+\sqrt{b^2-4ac}}{2a}\)
Wie du siehst besitzt die Mitternachtsformel zwei Lösungen \(x_{1/2}\), denn eine quadratische Funktion kann bis zu zwei Nullstellen haben. Eine quadratische Funktion kann keine, eine oder zwei Nullstellen besitzen. Um die Anzahl an Nullstellen zu bekommen musst du die Diskriminante
\(D=b^2-4ac\)
berechnen, dass ist der Term unter der Wurzel in der Mitternachts-Formel. Es gilt:
Regel:
Die Anzahl an Nullstellen erhältst du über die Diskriminante
- Wenn \(D < 0\) ist, dann existiert keine Nullstelle.
- Wenn \(D=0\) ist, dann existiert genau eine Nullstelle.
- Wenn \(D > 0\) ist, dann existieren zwei Nullstellen.
In der unteren Abbildung sind zwei Funktionen dargestellt. Die eine Funktion (Blau) besitzt keine Nullstellen, Sie befindet sich vollständig oberhalb der \(x\)-Achse und die andere Funktion (Rot) besitzt zwei Nullstellen.
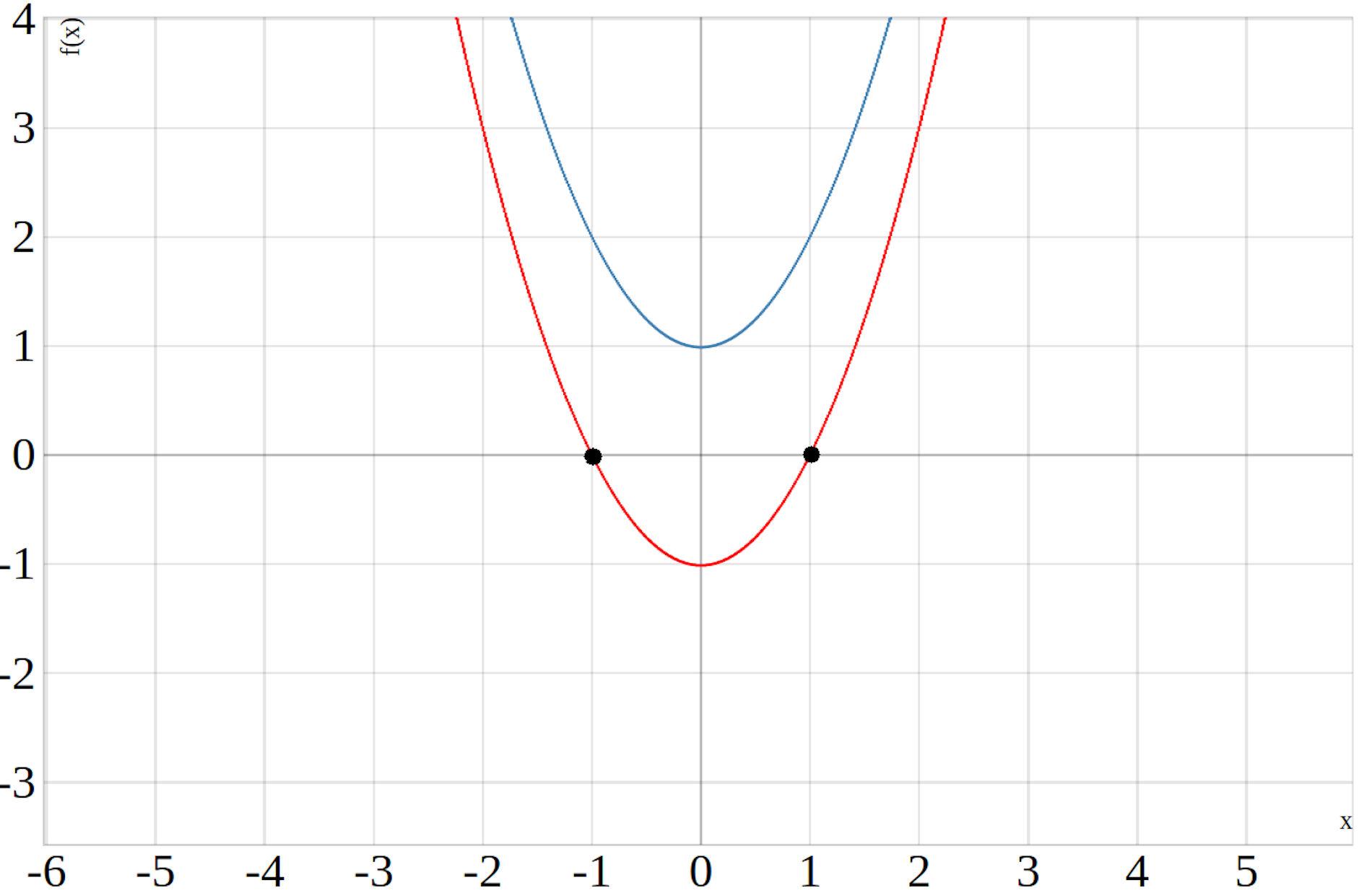
Regel:
Eine quadratische Funktion kann keine, eine oder zwei Nullstellen besitzen.
Die Nullstellen von \(f(x)=ax^2+bx+c\) berechnen sich mit der Mitternachtsformel:
\(x_{1/2}=\)\(\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
Nullstellen berechnen von Parabeln:
Parabeln in die Normalform bringen.
\(a,b\) und \(c\) aus der Normalform ablesen.
\(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
Mitternachtsformel ausrechnen.
Beispiel 1:
Berechne die Nullstellen der folgenden Funktion:
\(f(x)=2x^2-12x-14\)
Die Funktion befindet sich schon in der Normalform. Wir können also direkt zum zweiten Schritt übergehen und \(a,b\) und \(c\) ablesen.
\(a=2,\) \(b=-12\) und \(c=-14\)
Nun müssen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-(-12)\pm\sqrt{(-12)^2-4\cdot 2\cdot (-14)}}{2\cdot 2}\\ \\ &=\frac{12\pm\sqrt{144+112}}{4}\\ \\ &=\frac{12\pm\sqrt{256}}{4}\\ \\ &=\frac{12\pm 16}{4}\\ \end{aligned}\)
Fallunterscheidung:
\(x_{1}=\)\(\frac{12-16}{4}\)\(=-1\)
\(x_{2}=\)\(\frac{12+16}{4}\)\(=7\)
Die Nullstellen der Parabel befinden sich somit bei:
\(\begin{aligned} x_1&=-1\\ &\text{und}\\ x_2&=7 \end{aligned}\)
Beispiel 2:
berechne die Nullstellen der Funktion
\(f(x)=4x^2-16x+16\)
Die Funktion befindet sich bereits in der Normalform. Wir können also direkt zum zweiten Schritt übergehen und \(a,b\) und \(c\) ablesen.
\(a=4,\) \(b=-16\) und \(c=16\)
Nun müssen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-(-16)\pm\sqrt{(-16)^2-4\cdot 4\cdot 16}}{2\cdot 4}\\ \\ &=\frac{16\pm\sqrt{256-256}}{8}\\ \\ &=\frac{16\pm\textcolor{blue}{\sqrt{0}}}{8}\\ \\ &=\frac{16\pm 0}{8}\\ \\ &=\frac{16}{8}\\ \\ &=2\\ \end{aligned}\)
In diesem Beispiel hat die Parabel nur eine Nullstelle, da
die Diskriminante \(D\) gleich Null ist.
\(D=b^2-4ac=0\)
Die einzige Nullstelle befindet sich bei \(x_0=2\).
Beispiel 3:
Berechne die Nullstelle der Funktion
\(f(x)=2x^2-8x+11\)
Die Funktion befindet sich bereits in der Normalform. Wir können also direkt zum zweiten Schritt übergehen und \(a,b\) und \(c\) ablesen.
\(a=2,\) \(b=-8\) und \(c=11\)
Nun müssen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ &=\frac{-(-8)\pm\sqrt{(-8)^2-4\cdot 2\cdot 11}}{2\cdot 2}\\ &=\frac{8\pm\sqrt{64-88}}{4}\\ &=\frac{16\pm\textcolor{red}{\sqrt{-24}}}{4}\\ \end{aligned}\)
Wir müssen hier wieder die Wurzel einer negativen Zahl berechnen \(\sqrt{-24}\). Die Wurzel einer negativen Zahl ist jedoch nicht definiert. Die Parabel besitzt also keine Nullstellen, Sie befindet sich vollständig oberhalb der \(x\)-Achse.
Mit dem Nullstellen berechner kannst du die Nullstellen solcher Funktionen berechnen lassen. Gib dazu am besten zur Probe mal \(x^2+2x-5=0\) ein, und clicke auf Lösen. Du erhältst die Nullstellen, den Graphen der Funktion und den dazugehörigen Rechenweg.
Hier kommst du zum Rechner.
Nullstellen der e-Funktion
Die Exponential Funktion
\(f(x)=e^x\)
kann entweder keine Nullstelle oder höchsten eine Nullstelle besitzen.
Mit dem Nullstellen berechner kannst du die Nullstellen von Exponential Funktionen leicht ausrechnen und somit deine Ergebnisse Prüfen.
Beispiel 1
Berechne die Nullstelle der Funktion
\(f(x)=e^x\)
Diese Funktion besitzt keine Nullstellen. Die kann man zeigen, indem man die Funktionsgleichung Nullsetzt und dann nach \(x\) umstellt.
\(\begin{aligned} 0&=e^x\\ \\ 0&=e^x\,\,\,\,\,|ln(...)\\ \\ ln(0)&=ln(e^x) \end{aligned}\)
Der \(ln(0)\) ist nicht definiert, daher müssen wir die Berechnung der Nullstelle hier abbrechen. Die Funktion besitzt keine Nullstelle.
Beispiel 2
Berechne die Nullstelle der Funktion
\(f(x)=e^{x-1}-2\)
Zur Nullstellen Berechnung werden wir die Funktionsgleichung wieder Nullsetzen und dann die Gleichung nach \(x\) umstellen.
\(\begin{aligned} 0&=e^{x-1}-2\\ \\ 0&=e^{x-1}-2\,\,\,\,\,|+2\\ \\ 2&=e^{x-1}\,\,\,\,\,|ln(...)\\ \\ ln(2)&=ln(e^{x-1})\\ \\ ln(2)&=x-1\,\,\,\,\,|+1\\ \\ ln(2)+1&=x \end{aligned}\)
Die Nullstelle befindet sich bei
\(x=ln(2)+1\)
Die Koordinaten der Nullstelle lauten:
\(\{ln(2)+1,0\}\)
Die Funktion besitzt also genau eine Nullstelle. Die Nullstellen solcher Funktionen kannst du mit dem Nullstellen berechner ausrechnen und dir den Rechenweg anzeigen lassen.
