Wahrscheinlichkeitsrechnung
Online Rechner mit Rechenweg
Mit dem Online Rechner von Simplexy kannst du viele Matheaufgaben lösen und dabei auch den Lösungweg erhalten.
Wahrscheinlichkeitsrechnung
Einführung:
Beim Werfen einer Münze kann nicht vorhergesagt werden, ob die Münze Kopf oder Zahl anzeigen wird. Man weiß zwar das einer der beiden Ereignisse eintreten wird, kann aber nicht mit absoluter sicherheit eine Vorhersage treffen. In solch einem Fall bedient man sich der Wahrscheinlichkeitsrechnung um wenigstes die Chance mit der ein Ereigniss eintretten kann zu quantifizieren.
Die möglichen Ereignisse und deren Wahrscheinlichkeiten kann man in ein sogenanntes Baumdiagramm skizzieren, dieses Liefert einem sehr schnell Informationen über das Zufallsexperiment. Wie genau das geht wirst du später noch sehen. Es ist bereits das Wort Zufallsexperiment gefallen, was ist ein Zufallsexperiment ?
Zufallsexperiment
Ein Zufallsexperiment ist ein Versuch, dessen Ausgang nicht vorhersagbar ist, der Ausgang hängt also vom Zufall ab.
Eigenschaften eines Zufallsexperiments:
- Es gibt mehrere mögliche Ausgänge bzw. Ergebnisse.
- Man kann das Experiment beliebig of wiederholen.
- Es können nicht zwei Ergebnisse gleichzeitig eintreten.
- Man kann das Ergbniss nicht vorhersagen.
- Während des versuchs dürfen die Reglen und Bedindungen nicht geändert werden.
Einpaar Beispiele für Zufallsexperimente:
- Werfen eines Würfels.
- Werfen einer Münze.
- Ziehen einer Karte aus einem gemischtem Deck.
- Drehen eines Glückrades.
Versuche bei denen der Ausgang nicht zufällig ist, sondern berechnbar oder vorhersagbar ist, sind keine Zufallsexperimente.
Regel
Ein Versuch heißt Zufallsexperiment, wenn
- seine Bedingungen sich nicht ändern,
- er beliebig oft wiederholt werden kann,
- alle möglichen Ergebnisse bekannt sind,
- seine Bedingungen sich nicht ändern,
- sein Ereigniss nicht exakt vorhergesagt werden kann.
Einstufige Zufallsexperimente
Regel
Man nennt ein Zufallsexperiment, dass nur einmal durchgeführt wird einstufig
Beispiele für einstufige Zufallsexperimente:
- Einmaliges Werfen eines Würfels.
- Einmaliges Werfen einer Münze.
- Einmaliges Ziehen einer Karte aus einem gemischtem Deck.
- Einmaliges Drehen eines Glückrades.
Mehrstufige Zufallsexperimente
Man nennt ein Zufallsexperiment, dass mehr als einmal durchgeführt wird Mehrstufig.
Beispiele für einstufige Zufallsexperimente:
- zweimaliges Werfen eines Würfels.
- siebenmaliges Werfen einer Münze.
- dreimaliges Ziehen einer Karte aus einem gemischtem Deck.
Baumdiagramm
Ein Baumdiagramm oder auch Ereignisbaum genannt, ist eine graphische Darstellung, die Beziehungen zwischen einzellnen Ereignissen darstellt. Jeder Ast eines Baumdiagramms steht für ein mögliches Ereigniss. Wenn man nach der Wahrscheinlichkeit eines bestimmten Ereignisses gefragt wird, so muss man lediglich den jeweiligen Pfad bis zum gewollten Ereigniss folgen.
Regel
Ein Baumdiagramm, ist eine graphische Darstellung, mit der alle möglichen Ereignisse eines mehrstufigen Zufallversuchs in Beziehung gesetzt werden.
Mit dessen Hilfe können Wahrscheinlichkeiten für das Eintreffen eines Ereignisses berechnet werden.
Beispiel
In einer Urne befinden sich \(4\) blaue und \(5\) rote Kugeln.
Wir ziehen zwei Kugeln
a) mit zurckrücklegen
b) ohne zurckrücklegen
a) Baumdiagramm Ziehen mit zurücklegen
Erste Ziehung:
Da Insgesammt neun Kugeln in der Urne sind und davon \(4\) blau und \(5\) rot sind, ist die Wahrscheinlichkit beim ersten Zug eine blaue Kugel zu ziehen gerade \(\frac{4}{9}\). Die Wahrscheinlichkeit hingegen eine rote Kugel zu ziehen beträgt \(\frac{5}{9}\), da \(5\) von \(9\) Kugeln die farbe rot haben.
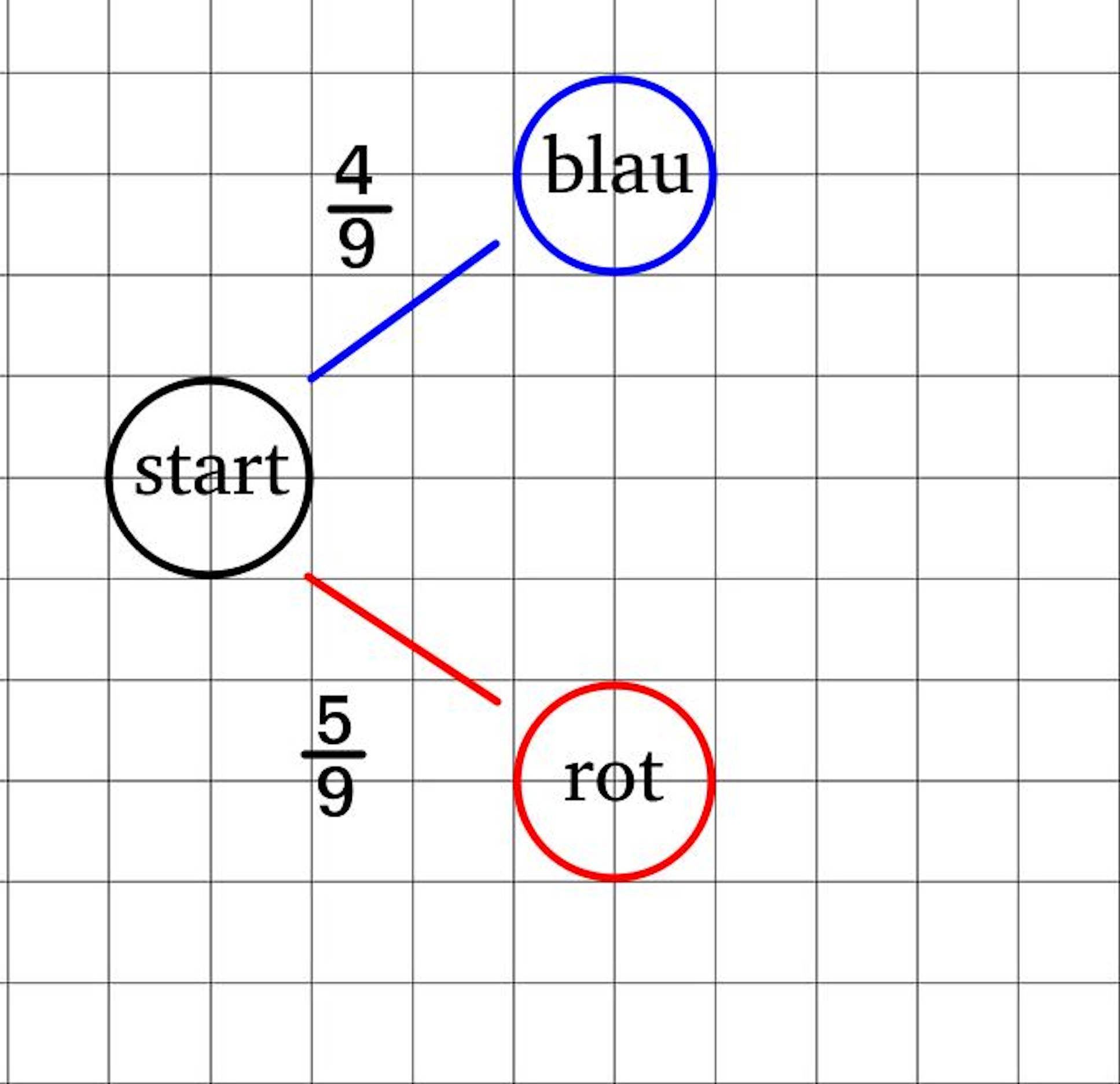
Zweite Ziehung:
Nach einem Zug wird die Kugel wieder in die Urne gelegt, damit ändert sich weder die Gesamtzahl der Kuglen noch die Anzahl an roten bzw. blauen Kugeln. Beim zweiten Zug sind also die Wahrscheinlichkeiten eine rote oder eine blaue Kugel zu ziehen genau so groß wie beim ersten Zug. An jeden der zwei Pfade vom ersten Zug kann man wieder zwei Pfade zeichnen, die den Zwei Pfanden des ersten Zuges identisch sind.
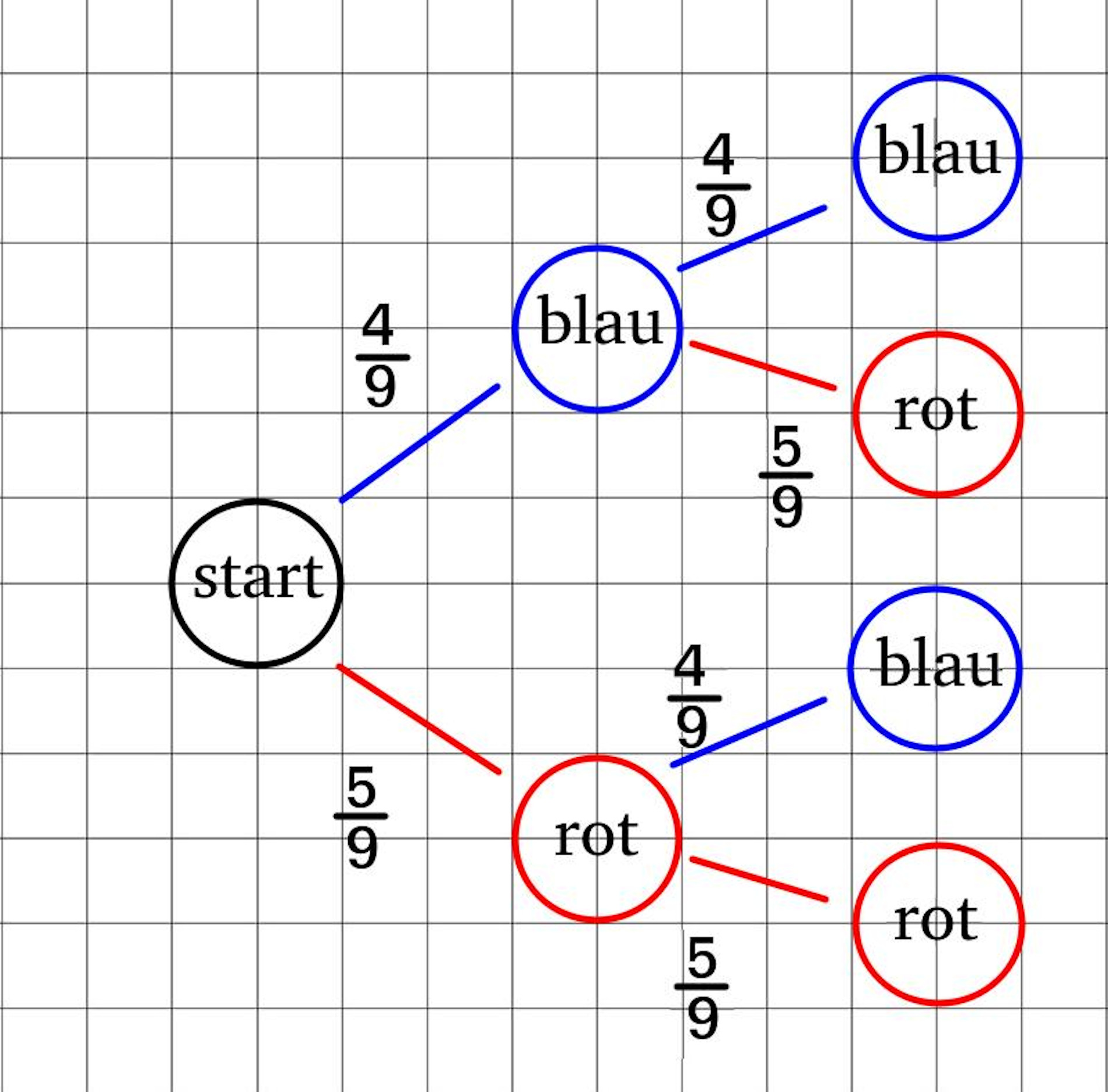
Nun kann man mit Hilfe des Baumdigramms berechnen wie groß die Wahrscheinlichkeit beträgt, im ersten Zug eine rote Kugel zu ziehen und anschließend im zweiten Zug eine blaue Kugel zu ziehen. Dazu muss man lediglich diesen Pfad suchen und die Wahrscheinlichkeiten entlang des Pfandes mit einander Multiplizieren. In diesem Fall ist die Wahrscheinlichkeit erst eine rote und dann eine blaue zu ziehen gerade
\(\frac{5}{9}\cdot \frac{4}{9}=\frac{20}{81}\approx 0,246\) das entspricht also einer wahrscheinlichkeit von etwa \(24,6\)%.
Womöglich ist dir Aufgefallen dass die Summe der Wahscheinlichkeiten auf den Ästenen, die von einem Verzweigungspunkt ausgehen, immer \(1\) ergibt.
Ausgehend vom Start (erste Vezweigung) gilt: \(\frac{5}{9}+\frac{4}{9}=1\)
Die Summe der Wahscheinlichkeiten auf den Ästenen die von einem Verzweigungspunkt ausgehen ist immer gleich \(1\).
Pfadregel
Die Wahrscheinlichkeit eines Elementarereignisses ist gleich dem Produkt der Wahrscheinlichkeiten des zugehörigen Pfades.
Beispiel
Wie groß ist die Wahrscheinlichkeit zwei mal hintereinander eine blaue Kugel zu ziehen ?
Wir nutzen die Pfadregel, die Wahrschinlichkeit beträgt also:
\(\frac{4}{9}\cdot\frac{4}{9}=\frac{16}{81}\approx0,197\) das entspricht einer Wahrscheinlichkeit von \(19,7\)%.
b) Baumdiagramm Ziehen ohne zurücklegen
In einer Urne befinden sich \(4\) blaue und \(5\) rote Kugelen, wir ziehen jeweils eine Kugel ohne sie wieder zurück in die Urne zu legen.
Erste Ziehung:
Da Insgesammt neun Kugeln in der Urne sind und davon \(4\) blau und \(5\) rot sind, ist die Wahrscheinlichkeit beim ersten Zug eine blaue Kugel zu ziehen gerade \(\frac{4}{9}\). Die Wahrscheinlichkeit hingegen eine rote Kugel zu ziehen beträgt \(\frac{5}{9}\), da \(5\) von \(9\) Kugeln die farbe rot haben.

Zweite Ziehung:
Da bereits einmal gezogen wurde und die Kugle nicht wieder in die Urne gelegt wurde, ist die Gesamtzahl der Kugeln in der Urne um eine Kugel weniger. In der Urne befinden sich also \(8\) Kugeln. Je nachdem ob beim ersten Zug eine rote oder eine blaue Kugel gezogen wurde, hat sich die Zahl der jeweiligen Kugeln mit der entsprechenden Farbe auch um \(1\) verringert. Wurde also beim ersten Zug eine blaue Kugel gezogen, dann befinden sich beim zweiten Zug nur noch \(3\) balue Kugeln in der Urne. Wurde jedoch eine rote Kugel beim ersten Zug gezogen dann sind beim zweiten Zug nur noch \(4\) rote Kugeln vorhanden.
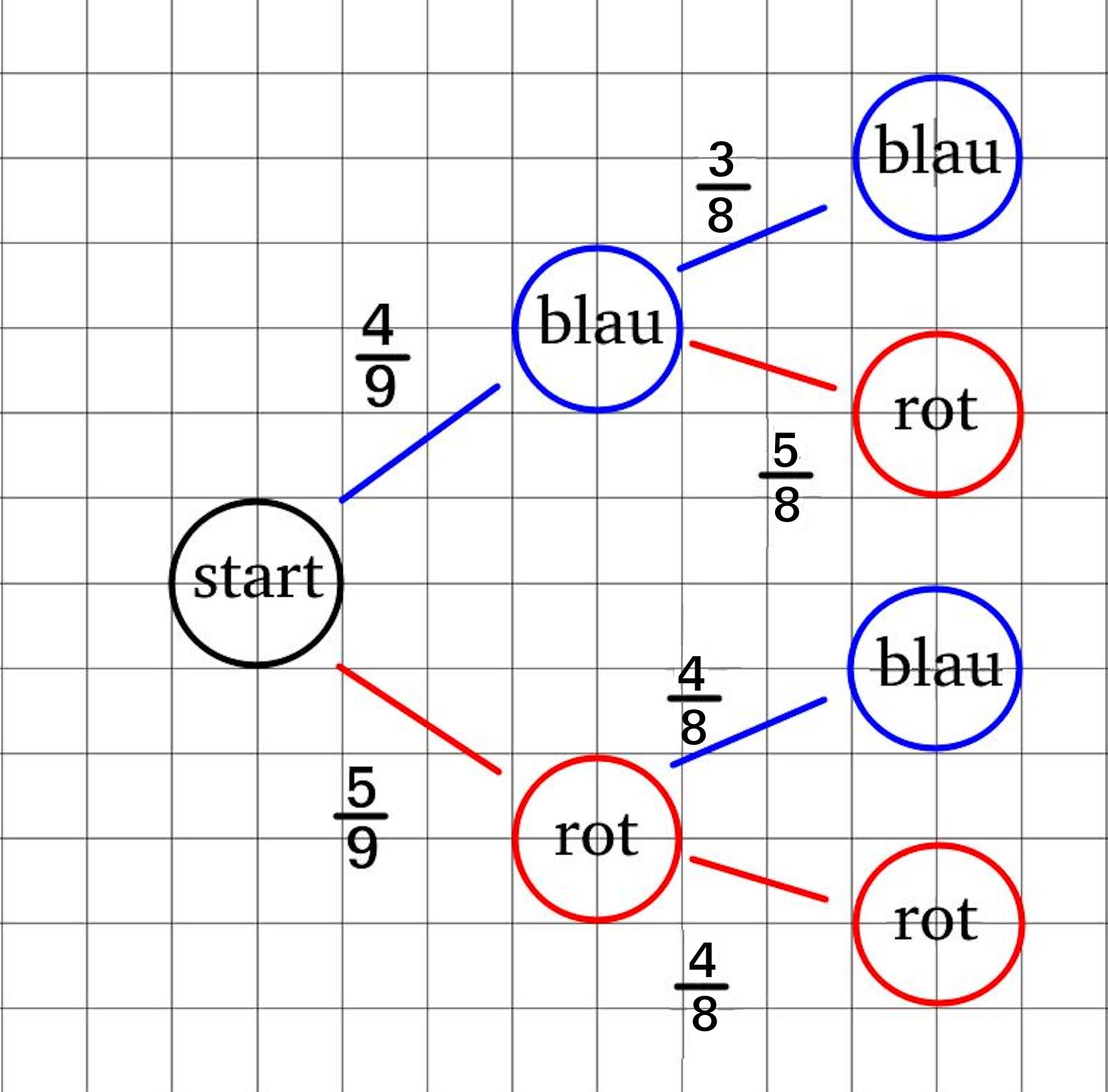
Auch hier gilt wieder, dass die Summe der Wahrscheinlichkeiten auf den Ästen, die von einem Verzweigungspunkt ausgehen, stets \(1\) ergibt.
- \(\frac{5}{9}+\frac{4}{9}=1\)
- \(\frac{3}{8}+\frac{5}{8}=1\)
- \(\frac{4}{8}+\frac{4}{8}=1\)
Ebenso so gilt auch die Pfadregel.
Die Warscheinlichkeit erst eine rote und anschließend eine blaue Kugel zu ziehen beträgt:
\(\frac{5}{9}\cdot\frac{4}{8}=\frac{20}{72}\approx 0,277\) das entspricht einer Wahrscheinlichkeit von \(27,7\)%.
