Wurzelfunktion
Wurzelfunktion Rechner mit Rechenweg
Simplexy besitzt einen Online Rechner mit Rechenweg. Probier den Rechner aus !
Wurzelfunktion
Einführung:
Was ist eine Wurzelfunktion?
Im allgemeinen sieht eine Wurzelfunktion folgendermaßen aus:
\(f(x)=\sqrt[n]{x}=\)\(x^{\frac{1}{n}}\)
- Man nennt \(n\in\mathbb{N}\) den Wurzelexponenten
- Das Argument der Funktion steht unter der Wurzel und wird Radikand genannt.
- Ist der Wurzelexponent eine gerade Zahl, so kann das Argument \(x\) nicht negativ sein. Das liegt daran, dass die Potenzfunktionen mit geradem Exponenten (\(x^2\),\(x^4\),\(x^6\),...) oberhalb der \(x\)-Achse verlaufen.
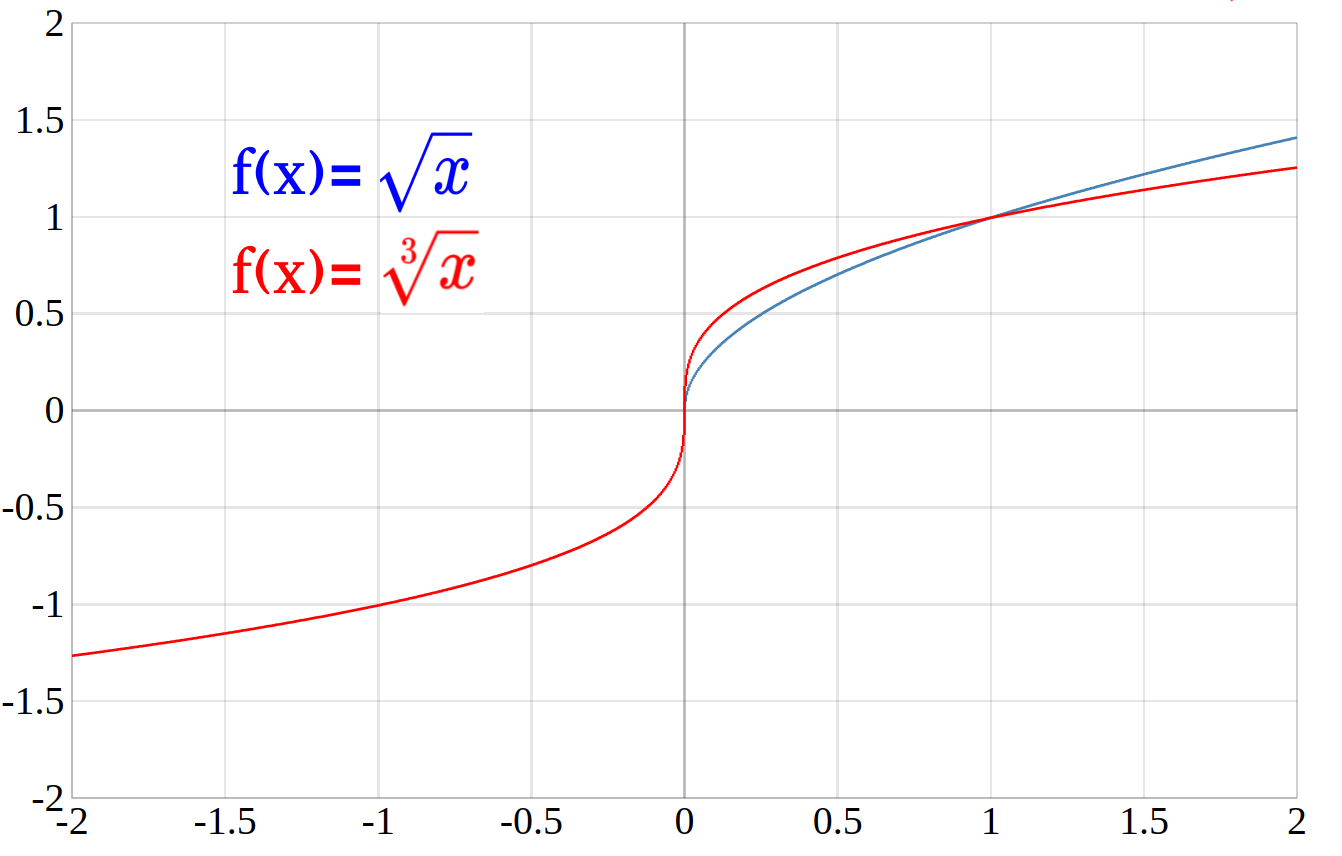
- Ist der Wurzelexponent ungerade, dann kann das Argument \(x\) auch negativ sein.
- Für positive Wurzelexponenten verläuft der Graph monoton wachsend.
- Es gilt: \(\sqrt[n]{0}=0\) für alle \(n\in\mathbb{N}\,\, \implies\) Die einzige Nullstelle von Wurzelfunktionen liegt bei \(x=0\)
- Es gilt \(\sqrt[n]{1}=1\) für alle \(n\in\mathbb{Z}\)
- Wurzelfunktionen sind die Umkehrfunktionen der Potenzfunktionen.
- Bei der Quadratwurzel verwendet man folgende Bezeichnung: \(\sqrt[2]{x}=\sqrt{x}\).
Tip: Mit dem Rechner von Simplexy kannst du die Graphen von beliebigen Funktionen erstellen.
Hier kommst du zum Rechner.
Umkehrfunktion einer Potenzfunktion
Eine Potenzfunktion wird im allgemeinen geschrieben als
\(f(x)=x^n\) mit \(n\in\mathbb{Z}\)
Eine Wurzelfunktion ist die Umkehrfunktion einer Potenzfunktion:
\(y=x^n \iff x=y^{1/n}=\sqrt[n]{y}\)
\(y=x^n \,\,\,\,\,\,\)\(|(...)^{\frac{1}{n}}\)
\(y^{\frac{1}{n}}=(x^n)^{\frac{1}{n}}=x^{n\cdot\frac{1}{n}}=x \)
\(\implies x=y^{1/n}=\sqrt[n]{y}\)
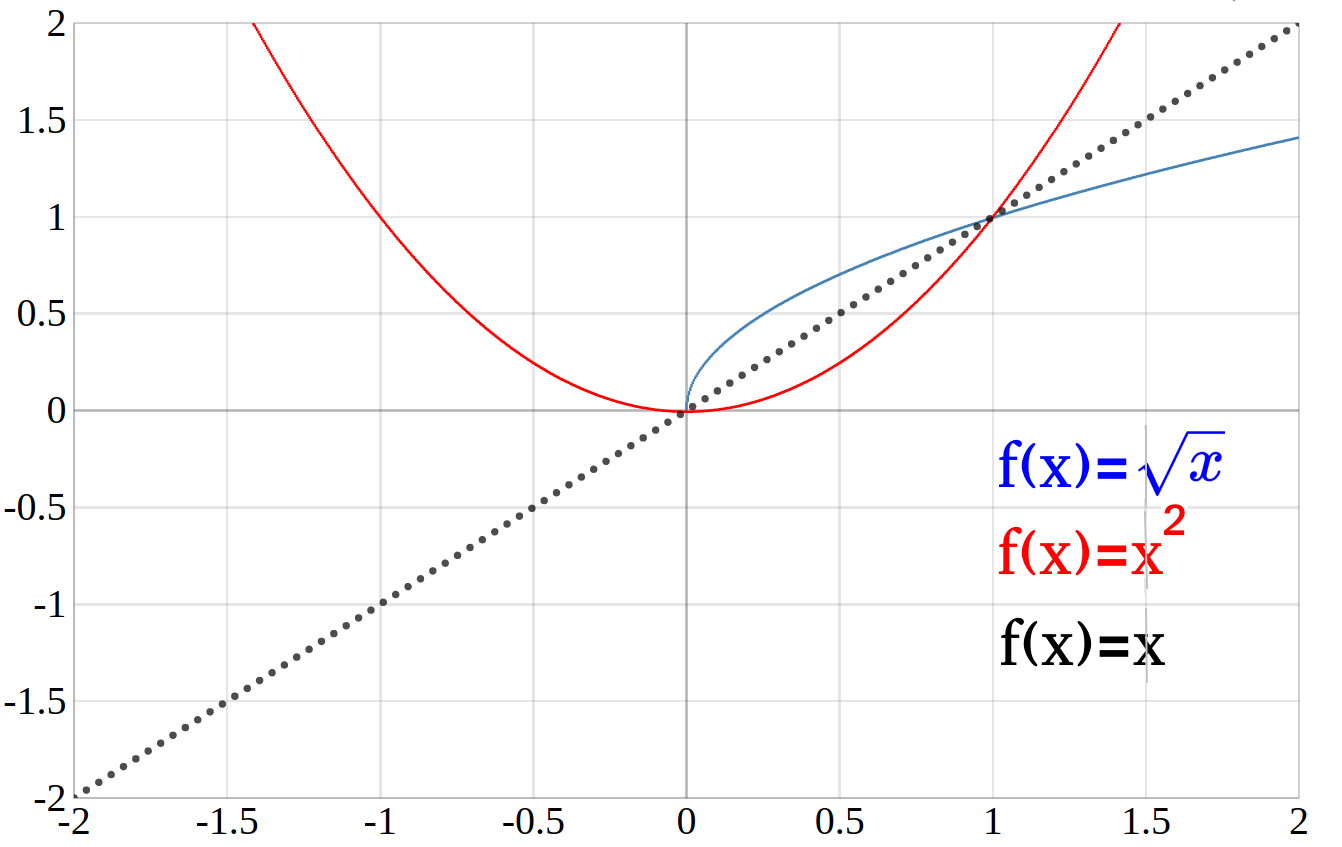
In der nächsten Abbildung sind die Funktionen
\(f(x)=x\), \(f(x)=x^2\) und \(f(x)=\sqrt{x}\) graphisch dargestelltn.