Cosinus Winkelfunktion
Cosinus Rechner
Simplexy besitzt einen Online Winkelfunktion Rechner. Probier den Rechner aus !
Cosinus
Mit der Cosinus-Funktion kann man das Verhältnis zweier Seiten in einem rechtwinkligen Dreieck berechnen.
Wie genau geht das ?
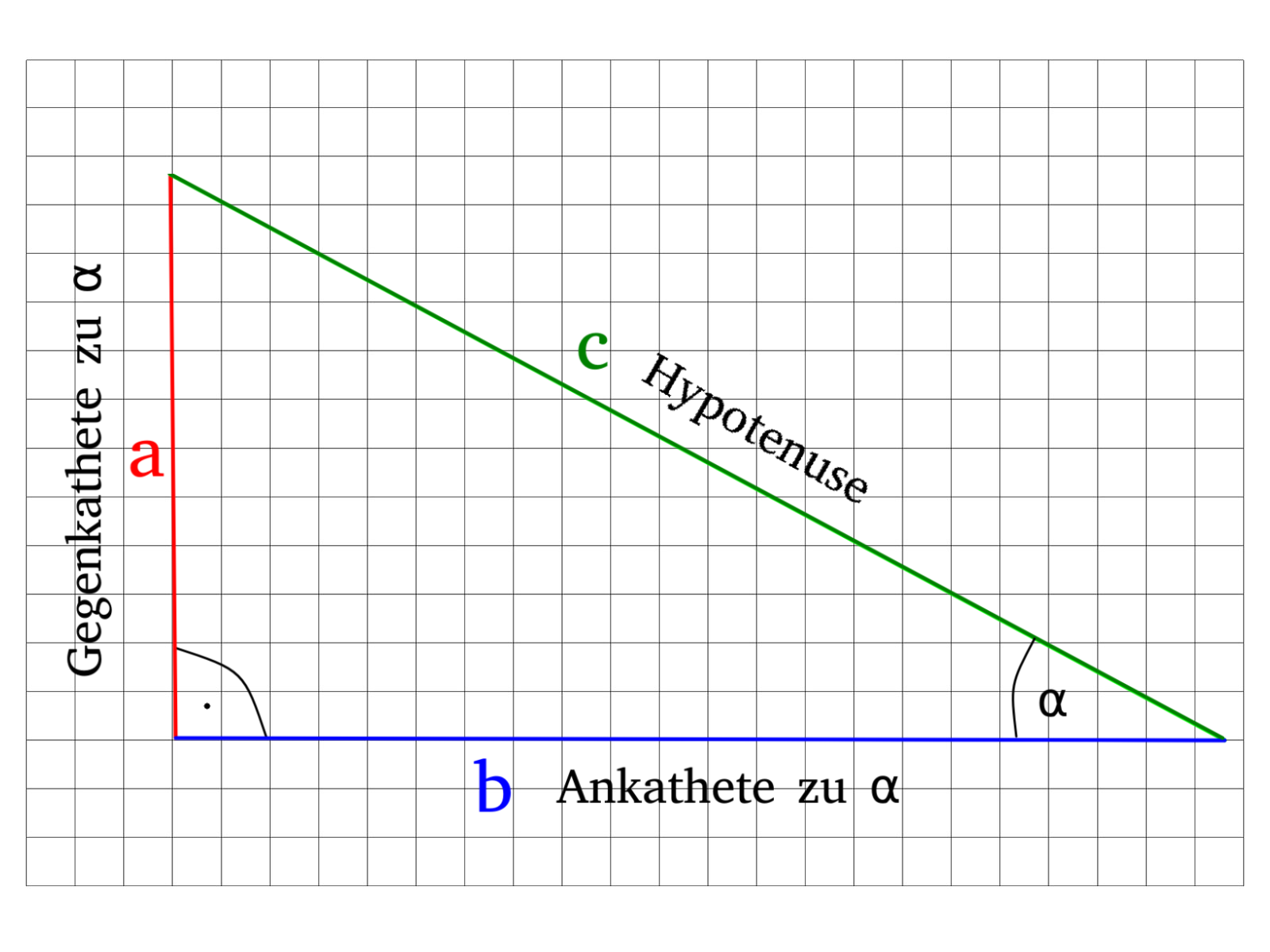
Wir benutzen zur Definition der Winkelfunktionen die obere Abbildung. Dabei steht der Winkel \(\alpha\) im Fokus.
Im Bezug auf den Winkel \(\alpha\), ist die Seite \(a\) die Gegenkathete und die Seite \(b\) die Ankathete. Also gilt:
- Die Seite \(a\) ist die Gegenkathete zu \(\alpha\)
- Die Seite \(b\) ist die Ankathete zu \(\alpha\)
- Die Seite \(c\) ist die Hypotenuse
Regel:
Das Verhältnis von Ankathete zu Hypotenuse wird als Cosinus des Winkels \(\alpha\) bezeichnet
\(cos(\alpha)=\)\(\frac{Ankathete}{Hypotenuse}=\frac{b}{c}\)
Cosinus Umkehrfunktion
Regel:
Die Umkehrfunktion vom Cosinus hat folgende Bezeichnungen .
- Die Umkehrfunktion von \(cos\) wird \(cos^{-1}\), \(acos\) oder \(arccos\) genannt.
Mit der Umkehrfunktion vom Cosinus ist es möglich den Winkel in einem rechtwinkligen Dreieck zu ermittelen, wenn einem die Seitenverhälnisse gegeben sind.
Es folgt ein Rechenbeispiel um dies zu verdeutlichen.
Regel:
\(cos^{-1}(cos(\alpha))=\alpha\)
Beispiel:
Gegeben ist das folgende Dreieck, wie groß ist der Winkel \(\alpha\) ?
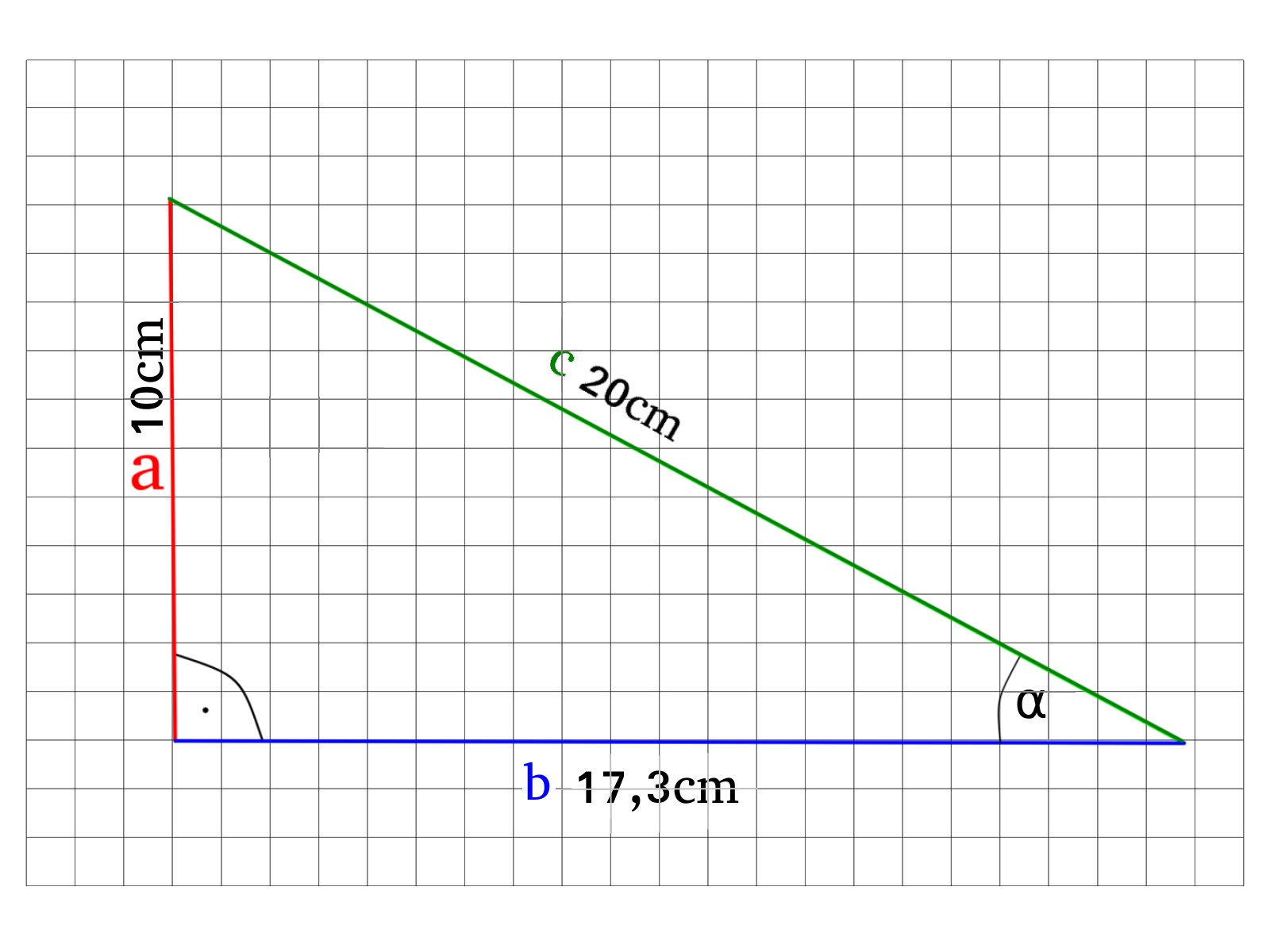
Da alle Seitenlängen des Dreiecks gegeben sind, können wir alle Seitenverhältnise selber ermitteln. Wir können dementsprechend frei wählen ob wir mit dem Sinus, Cosinus oder mit dem Tangens rechnen wollen. Wir entscheiden uns für den Cosinus.
Wir wissen bereits, dass folgendes gilt:
\(cos(\alpha)=\)\(\frac{Ankathete}{Hypotenus}=\frac{b}{c}\)
\(cos(\alpha)=\)\(\frac{17,3cm}{20cm}\)
\(cos(\alpha)=0,865\)
Um also auf den Winklen \(\alpha\) zu kommen müssen wir nur noch folgendes anwenden:
\(cos^{-1}(cos(\alpha))=\alpha\)
\(cos^{-1}(0,865)\approx 30°\)
Der Winkel \(\alpha\) ist ca. \(30°\) groß.
