Sinus Winkelfunktion
Sinus Rechner
Simplexy besitzt einen Online Sinus Rechner. Probier den Rechner aus !
Sinus
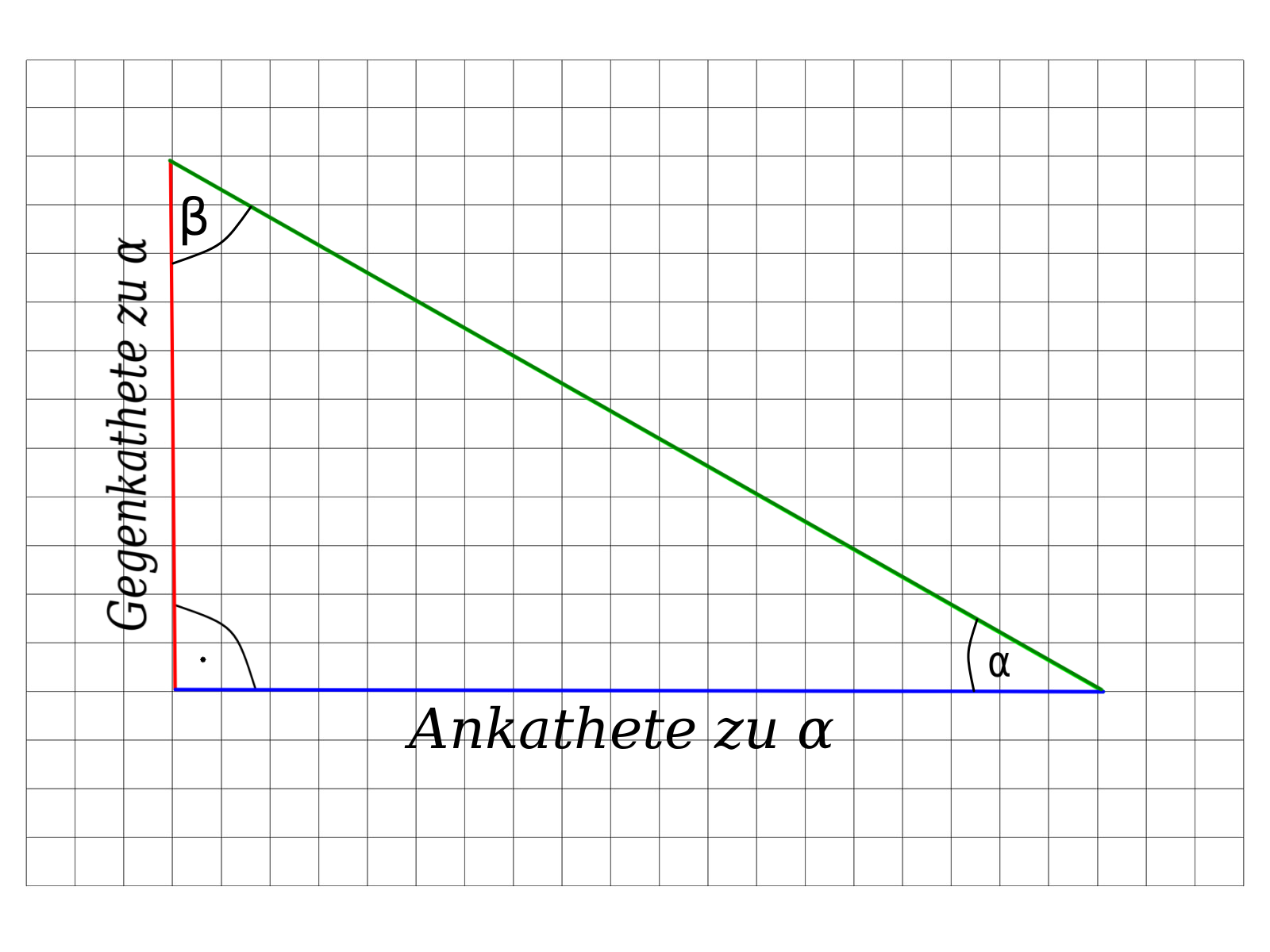
Regel:
- Die Ankathete ist die dem Winkel anliegende seite.
- Die Gegenkathete ist die dem Winkel gegen überliegende seite
Das Verhältnis zweier Seiten in einem rechtwinkligen Dreieck kann mit dem Sinus berechnet werden.
Wie genau wird der Sinus benutzt ?
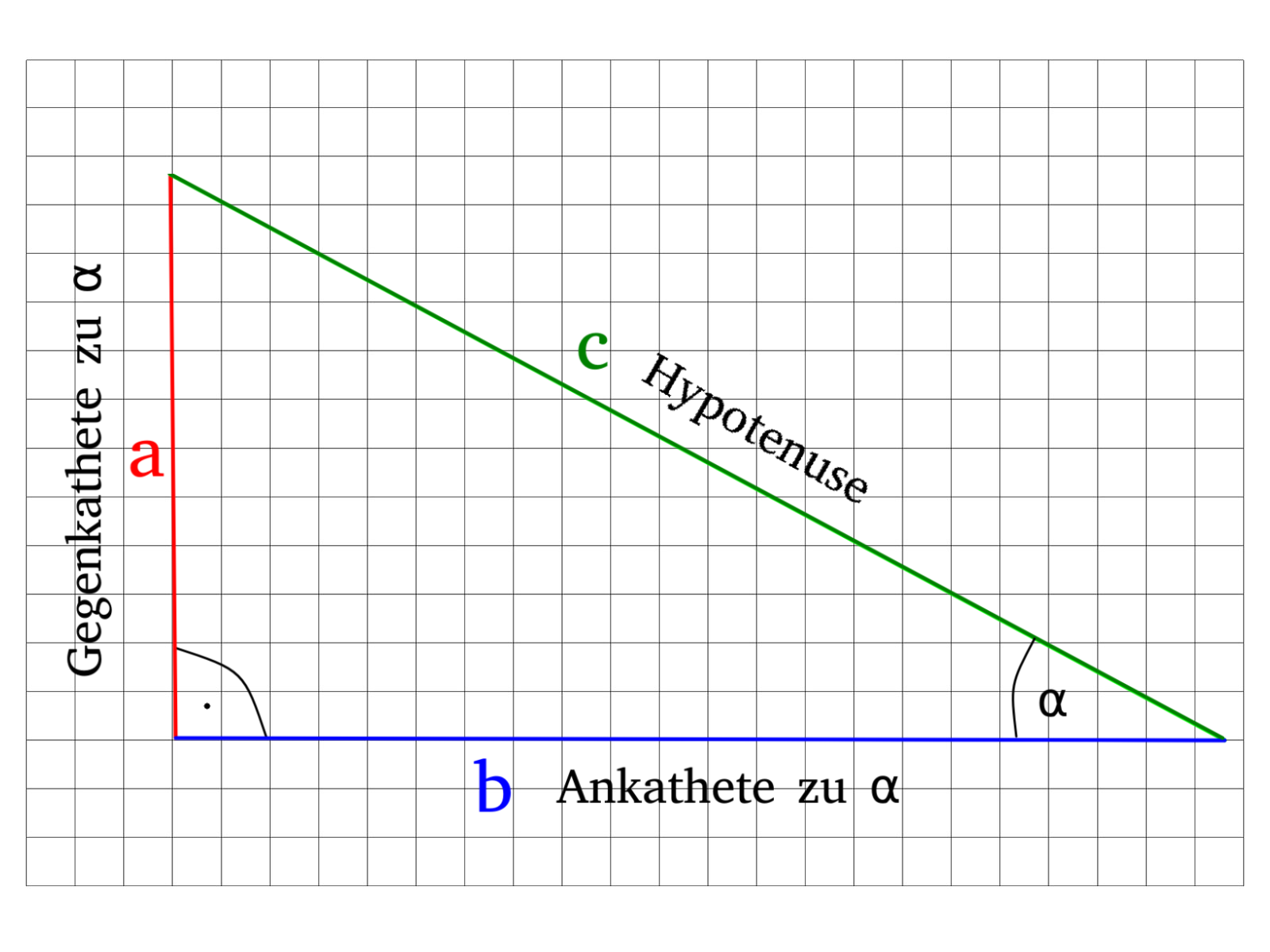
Zur Definition des Sinus nutzen wir die obere Abbildung. Der Winkel \(\alpha\) steht hierbei im Fokus.
Die Seite \(a\) ist die Gegenkathete und die Seite \(b\) ist die Ankathete zu \(\alpha\).
Es gilt:
- Die Seite \(a\) ist die Gegenkathete zu \(\alpha\)
- Die Seite \(b\) ist die Ankathete zu \(\alpha\)
- Die Seite \(c\) ist die Hypotenuse
Regel:
Das Verhältnis von Gegenkathete zu Hypotenuse wird Sinus genannt.
\(sin(\alpha)=\)\(\frac{Gegenkathete}{Hypotenuse}=\frac{a}{c}\)
Beispiel 1
Gegeben ist das folgende Dreieck, berechne die Länge der Seite \(a\).
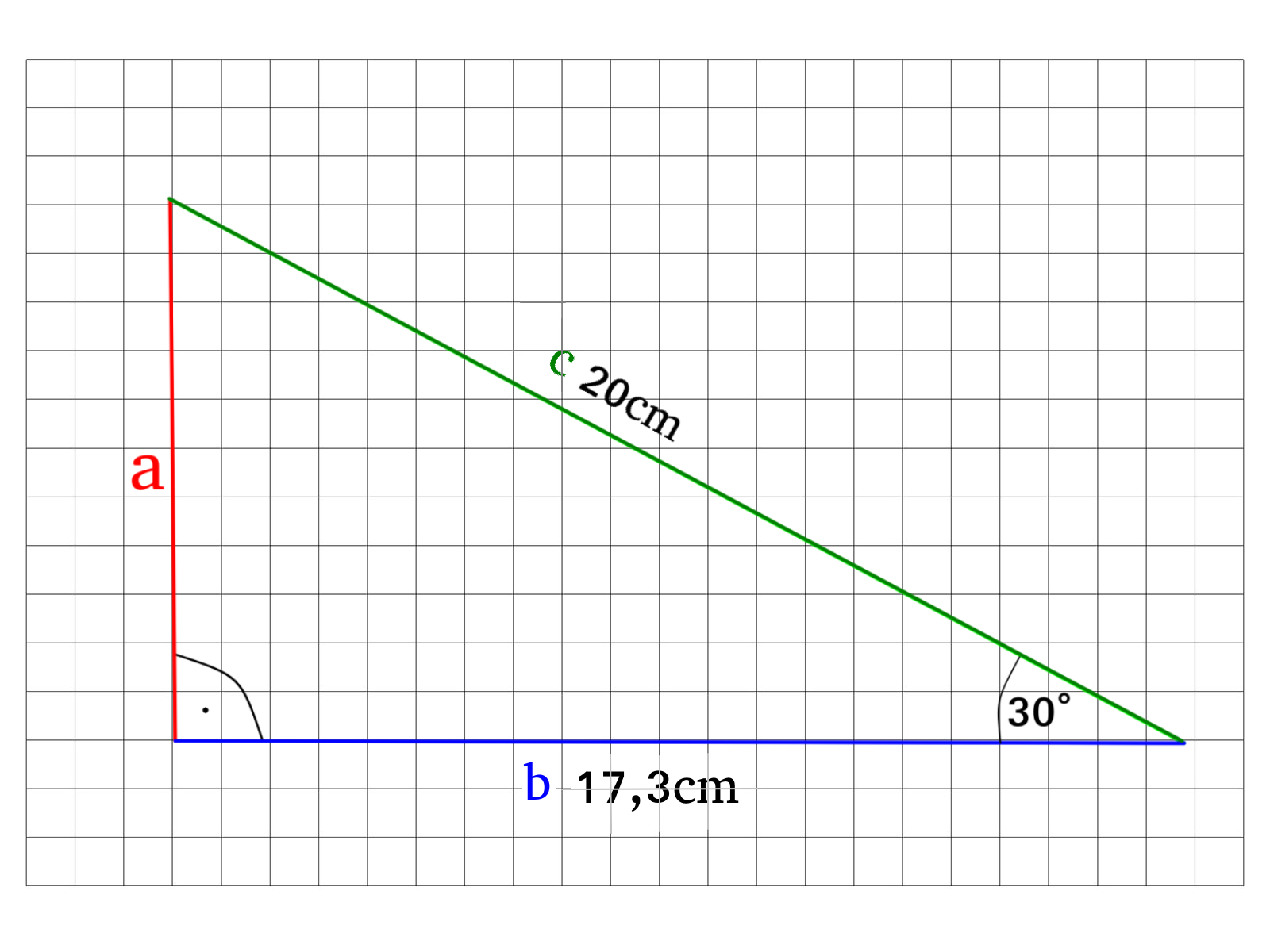
Lösung:
Wir nutzen den Sinus um das Seitenverhältnis von \(a\) und \(c\) zu ermitteln:
\(sin(30°)=\)\(\frac{a}{c}=\frac{a}{20cm}\)
Diese Gleichung können wir wie jede andere Gleichung umstellen, das Umstellen von Gleichungen kannst du hier wiederholen.
\(sin(30°)=\)\(\frac{a}{20cm}\)\(\,\,\,\,\,\,|\cdot 20cm\)
\(sin(30°)\cdot 20cm=a\)
Wir wissen jetzt, dass
\(a=sin(30°)\cdot 20cm\)
wir könnnen im Tachenrechner nach dem \(sin\) suchen und dann den \(sin(30°)\) berechen. Dabei ist zu beachten, das der Taschenrechner auf deg bzw. DEG eingestellt ist. Den \(sin(30°)\) kannst du auch mit dem Rechner von Simplexy berechnen. Der Rechner ist auch in der lage die Gleichung \(sin(30°)=\)\(\frac{a}{20}\) für dich zu lösen. Hier kommst du zum Rechner. Der Rechner von Simplexy rechnet automatisch mit der Einstellung 'deg' darum braucht du dich also bei Simplexy nicht mehr zu kümmern.
Wir geben im Taschenrecher \(sin(30)\) ein und erhalten:
\(sin(30)=0,5\)
Damit bekommen wir die gesuchte Seitenlänge
\(a=sin(30°)\cdot 20cm=0,5\cdot 20cm=10cm\)
Die Seite \(a\) ist \(10cm\) lang.
Sinus Umkehrfunktion
Bis jetzt hast du gesehen wie man mit dem Sinus, die Seitenverhälnisse in einem rechtwinklen Dreieck berechnet. Mit der Umkehrfunktion vom Sinus ist es möglich anhand eines Seitenverhälnisses den Winkel zu berechnen .
Regel:
Der Sinus besitzt eine Umkehrfunktion.
- Die Umkehrfunktion von \(sin\) wird \(sin^{-1}\), \(asin\) oder \(arcsin\) genannt.
Im oberen Beispiel hast du gesehen, dass \(sin(30)=0,5\) ist. Es gilt:
\(sin^{-1}(0,5)=30\)
Was genau ist hier passiert, schreiben wir das mal anderes auf:
\(sin^{-1}(0,5)=sin^{-1}(sin(30))=30\)
Man bezeichnet die Zahl die in den Klammern einer Funktion steht als Argument der Funktion, im Fall von \(sin(30)\) ist der Winkel \(30\) das Argument. Im Fall von \(sin^{-1}(0,5)\) ist das Argument \(0,5\). Es sieht so aus als könnte man mit der Funktion \(sin^{-1}\) herausfinden, was das Argument vom \(sin\) war.
Das Kann man auch allgemein schrieben als:
\(sin^{-1}(sin(\alpha))=\alpha\)
Regel:
\(sin^{-1}(sin(\alpha))=\alpha\)
Wie wendet man die Umkehrfunktion vom Sinus an ?
Beispiel
Gegeben ist das folgende Dreieck, wie groß ist der Winkel \(\alpha\) ?
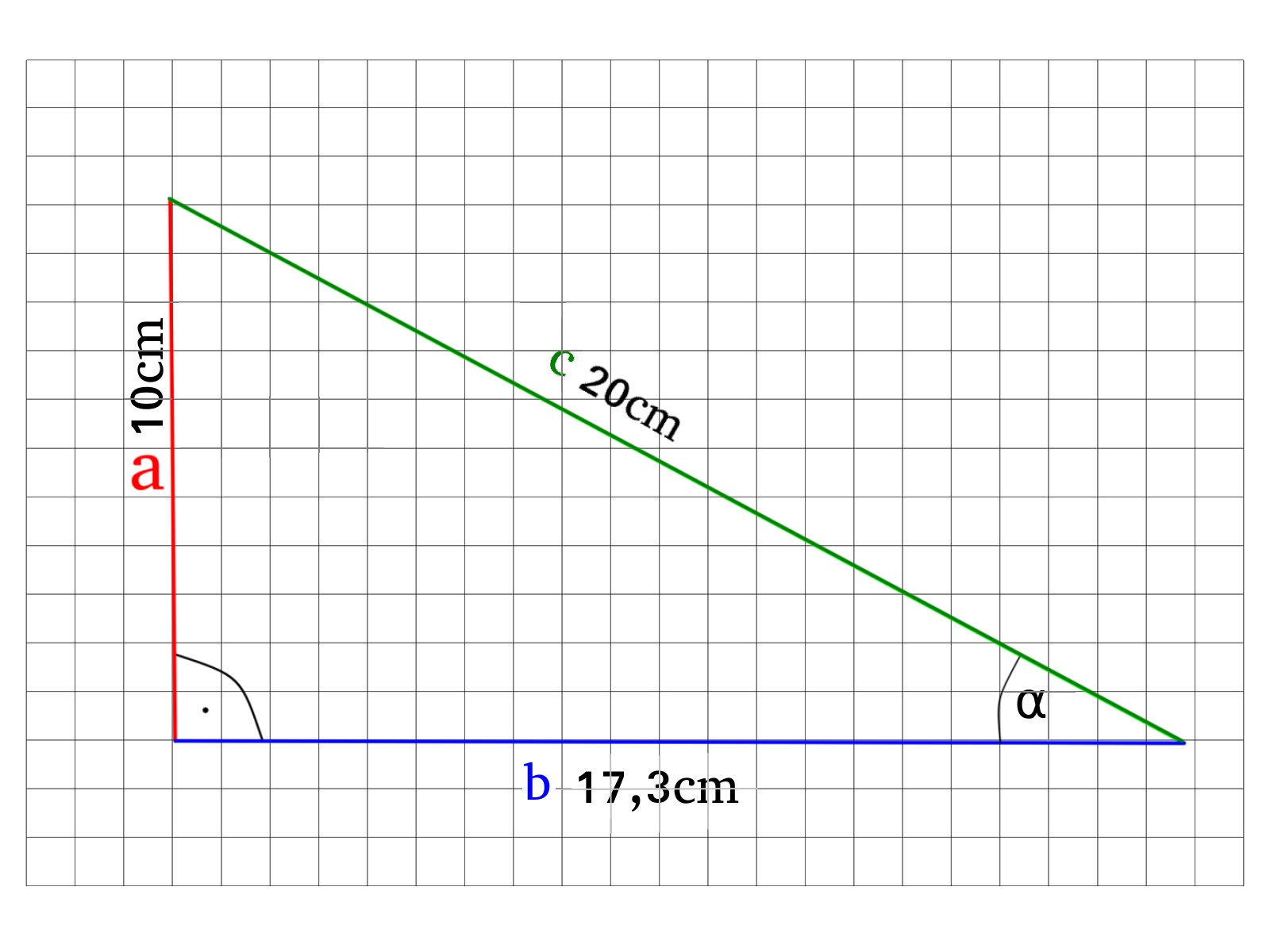
Bei so einer Aufgabe ist das Vorgehen sehr einfach, da uns alle drei Seiten gegeben sind können wir frei wählen, ob wir mir dem Sinus, Cosinus oder mit dem Tangens rechnen wollen. Wir entscheiden uns für den Sinus.
Wir wissen bereits, dass folgendes gilt:
\(sin(\alpha)=\)\(\frac{Gegenkathete}{Hypotenus}=\frac{a}{c}\)
\(sin(\alpha)=\)\(\frac{10cm}{20cm}\)
\(sin(\alpha)=0,5\)
Um also auf den Winklen \(\alpha\) zu kommen müssen wir nur noch folgendes anwenden:
\(sin^{-1}(sin(\alpha))=\alpha\)
\(sin^{-1}(0,5)=30°\)
Der Winkel \(\alpha\) ist ca. \(30°\) groß.
