Tangens Winkelfunktion
Tangens Rechner
Simplexy besitzt einen Online Winkelfunktion Rechner. Probier den Rechner aus !
Tangens
Mit der Tangens-Funktion kann man das Verhältnis zweier Seiten in einem rechtwinkligen Dreieck berechnen.
Wie genau geht das ?
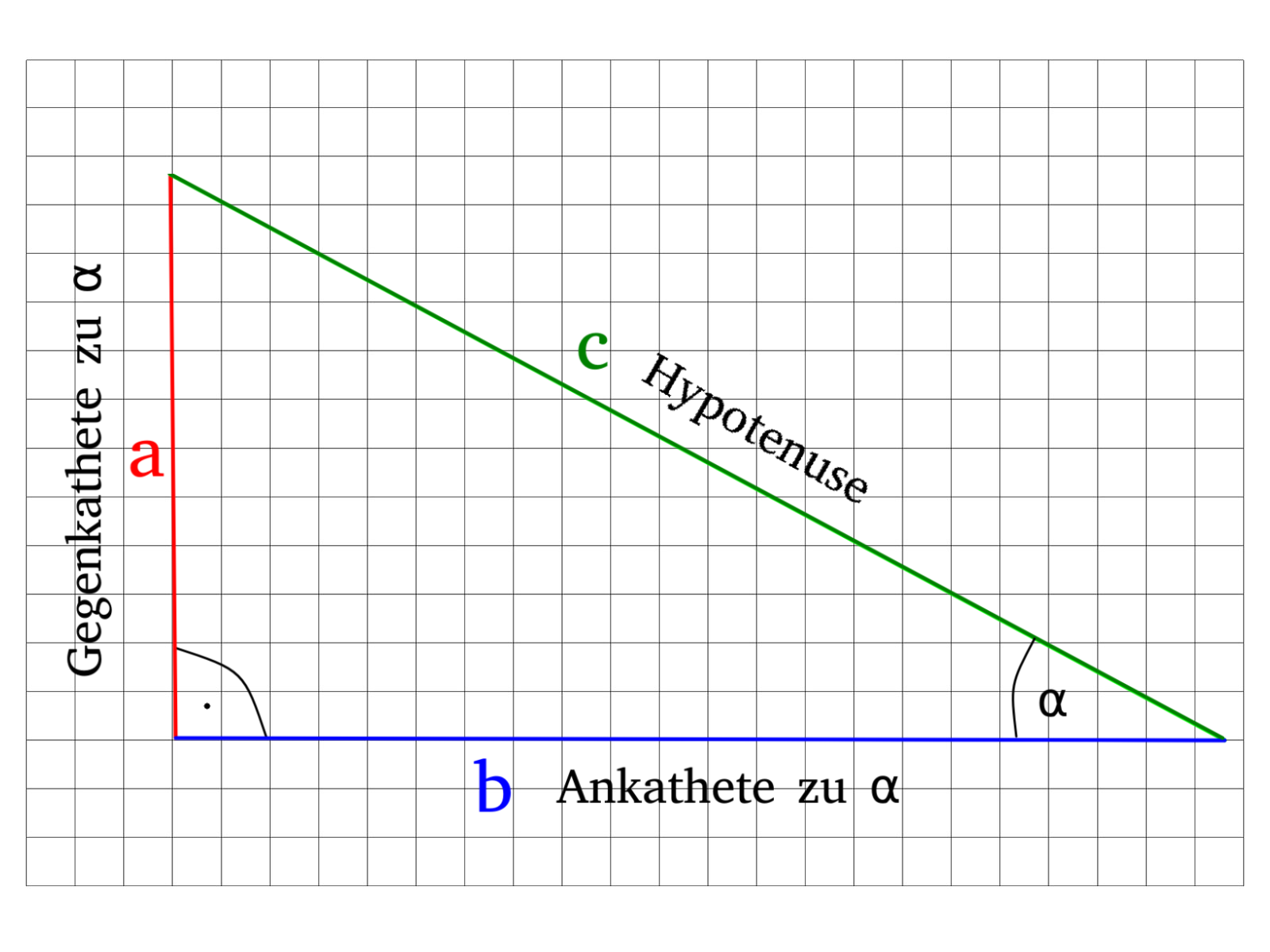
Wir benutzen zur Definition der Winkelfunktionen die obere Abbildung. Dabei steht der Winkel \(\alpha\) im Fokus.
Im Bezug auf den Winkel \(\alpha\), ist die Seite \(a\) die Gegenkathete und die Seite \(b\) die Ankathete. Also gilt:
- Die Seite \(a\) ist die Gegenkathete zu \(\alpha\)
- Die Seite \(b\) ist die Ankathete zu \(\alpha\)
- Die Seite \(c\) ist die Hypotenuse
Regel:
Das Verhältnis von Gegenkathete zu Ankathete wird Tangens des Winkels \(\alpha\) genannt.
\(tan(\alpha)=\)\(\frac{Gegenkathete}{Ankathete}=\frac{a}{b}\)
Beispiel:
Gegeben ist das folgende Dreieck, berechne die Länge der Seite \(a\).
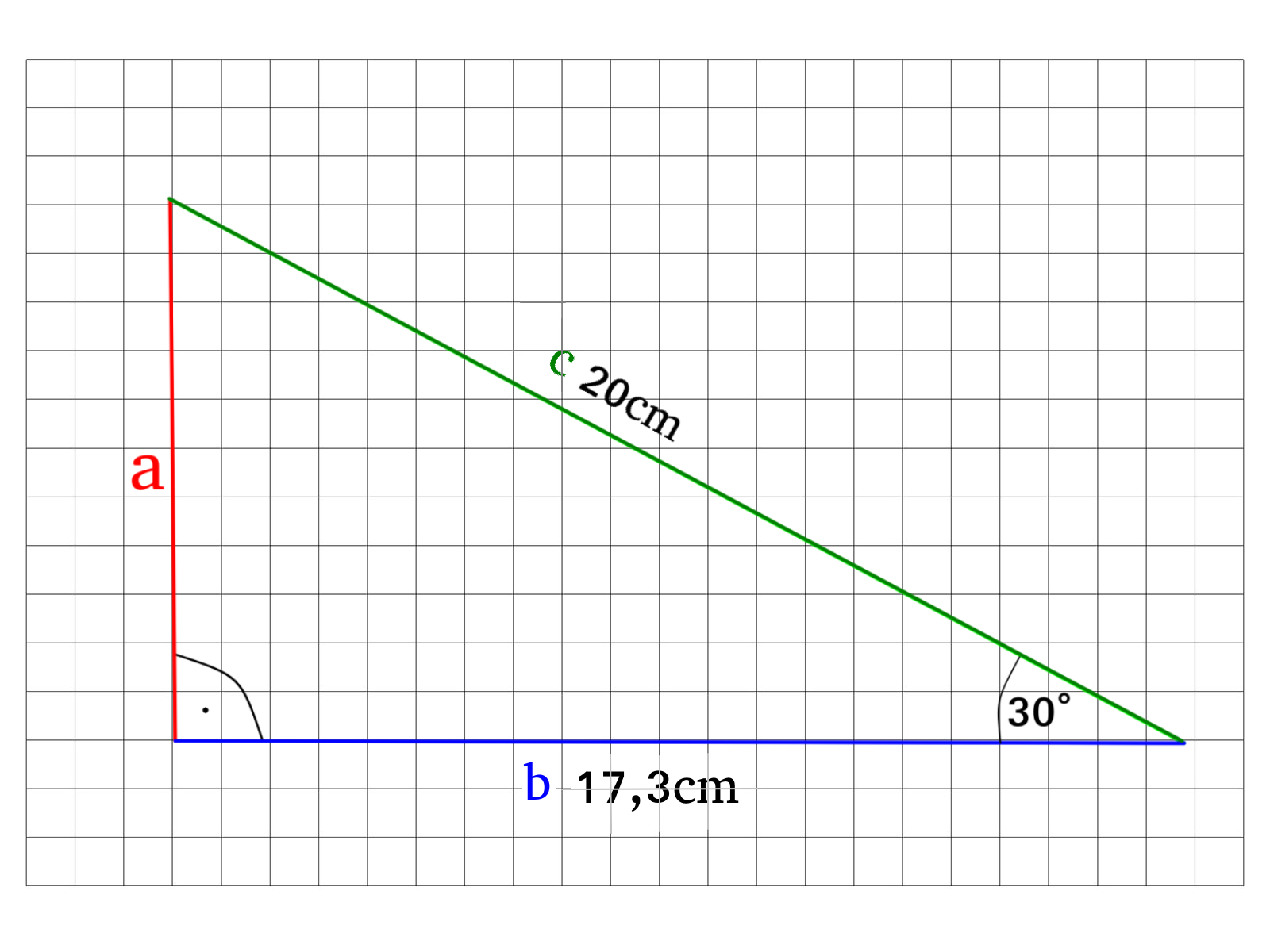
Wir nutzen den Tangens um das Seitenverhältnis von \(a\) und \(b\) zu ermitteln:
\(tan(30°)=\)\(\frac{a}{b}=\frac{a}{17,33cm}\)
\(tan(30°)=\)\(\frac{a}{17,33cm}\)\(\,\,\,\,\,\,|\cdot 17,33cm\)
\(tan(30°)\cdot 17,33cm=a\)
Du suchst im Taschenrechner nach dem tan knopf und berechnest \(tan(30)\). Nicht vergessen, der Taschenrechner muss auf deg bzw. DEG eingestellt sein.
\(tan(30)=0,577\)
Damit folgt:
\(tan(30°)\cdot 17,33cm=a\)
\(0,577\cdot 17,33cm=a\)
\(a=10,00cm\)
Die Länge von \(a\) beträgt \(10cm\).
Tangens Umkehrfunktion
Regel:
Die Umkehrfunktion vom Tangens hat verschiedene Bezeichungen .
- Die Umkehrfunktion von \(tan\) wird \(tan^{-1}\), \(atan\) oder \(arctan\) genannt.
Mit der Umkehrfunktion vom Tangens kann der Winkel in einem rechtwinkligen Dreieck ermittelt werden, dazu muss einem das geeignete Seitenverhälniss gegeben sind.
Es folgt ein Rechenbeispiel um dies zu verdeutlichen.
Regel:
\(tan^{-1}(tan(\alpha))=\alpha\)
