Fadenpendel Periodendauer
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Fadenpendel Zusammenfassung
Die Schwingungsgleichung vom Fadenpendel kann über die Betrachtung der Rückstellkraft ermittelt werden. Dabei ist die Rückstellkraft gerade die Tangentialkomponente der Gewichtskraft.
Die Schwingungsgleichung vom Fadenpendel lautet:
\(\begin{aligned} \ddot{x}(t)+\frac{g}{l}\cdot x(t)=0 \end{aligned}\)
Dabei ist:
\(x(t)\) die Auslenkung.
\(l\) die Länge des Fadens.
\(g\) die Fallbeschleunigung.
Das Fadenpendel schwingt harmonisch mit der Ort-Zeit-Funktion
\(x(t)=x_0\cdot cos(\omega\cdot t)\)
Dabei ist \(\omega\) die Eigenfrequenz bzw. Kreisfrequenz des Pendels.
\(x_0\) ist die Startauslenkung des Pendels.
\(\begin{aligned} \omega=\sqrt{\frac{g}{l}} \end{aligned}\)
Die Schwingungsdauer bzw. die Periodendauer berechnet sich über
Die Frequenz berechnet sich über
\(\begin{aligned} T=\frac{2\pi}{\omega} \end{aligned}\)
\(\begin{aligned} T=2\pi\cdot\sqrt{\frac{l}{g}} \end{aligned}\)
\(\begin{aligned} f=\frac{1}{T} \end{aligned}\)
Fadenpendel Periodendauer
Die Periodendauer gibt an, wie lange ein schwingungsfähiges System für eine vollständige Schwingung benötigt. Lenkt man ein Fadenpendel aus und lässt es dann los, so wäre die Periodendauer, die Zeit die das Pendel benötigt um wieder zurück zur start Auslenkung zu gelangen.
In dem unteren Video ist die Periodendauer vom Fadenpendel leicht erklärt.
Wie man dem Video entnehmen kann, ist die Periodendauer vom Fadenpendel genau die Zeit, die das Pendel benötigt um eine vollständige Periode (hin und her Bewegung) durchzuführen. Diese Zeit können wir bestimmen, indem wir die Zeit zwischen zwei Maxima der Ort-Zeit-Funktion ermitteln. Im unteren Bild ist dieses Vorgehen schematische dargestellt.
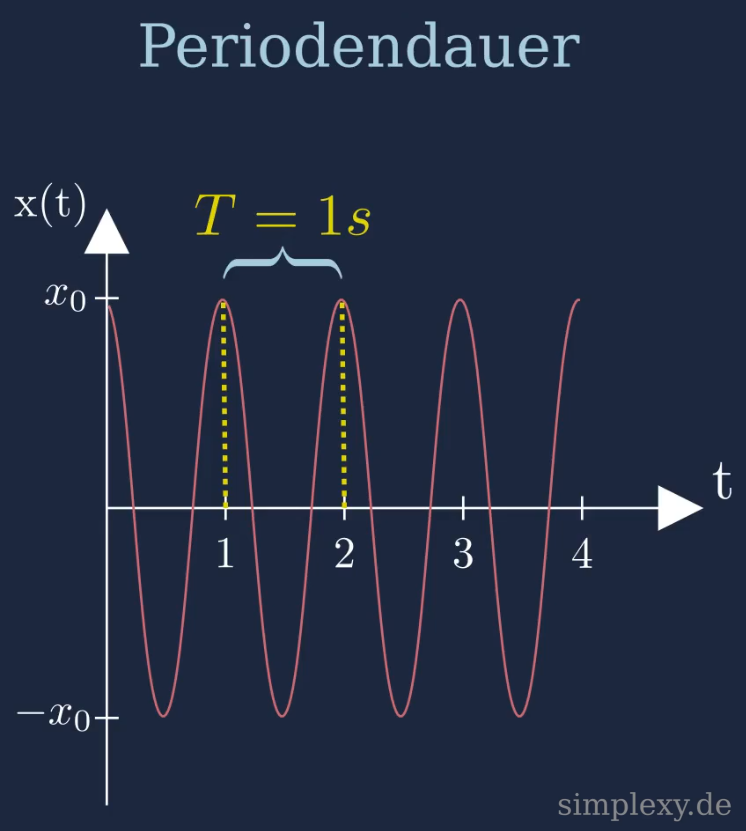
In dem Bild sehen wir, dass ein Maximum der Auslenkung bei der Zeit \(t_1=1s\) und ein Maximum bei der Zeit \(t_2=2s\) vorhanden ist.
Die Differenz zwischen diesen zwei Zeiten ist die Periodendauer \(T\).
\(\begin{aligned} T&=t_2-t_1\\ &=2s-1s\\ &=1s \end{aligned} \)
In diesem Fall ist die Periodendauer genau \(T=1s\) lang.
Man muss für die Bestimmung der Periodendauer nicht immer die Maxima der Ort-Zeit-Funktion (Auslenkungsfunktion) benutzen. Das gleiche kann man mit den Minima, den Nullpunkten oder jeden anderen beliebigen Punkt machen. Wichtig ist nur, dass man die Zeit zwischen zwei identischen aufeinanderfolgenden Punkten betrachten.
Periodendauer
Die Periodendauer gibt an wie lange eine vollständige Schwingung dauert.
In dem unteren Video ist die Periodendauer vom Fadenpendel leicht erklärt.
Periodendauer und Frequenz
Die Frequenz und die Periodendauer stehen in einem engen Zusammenhang zu einander. Die Periodendauer gibt die Zeit für eine vollständige Schwingung an und die Frequenz gibt an wie viele Schwingungen in einer Sekunde vollführt werden.
Periodendauer
Die Periodendauer gibt an, wie lange eine vollständige Schwingungen des Federpendels dauert.
Die Periodendauer hat die Einheit \([s]\) Sekunde.
Je größer die Periodendauer ist, desto kleiner ist die Frequenz und je kleiner die Periodendauer ist, desto größer ist die Frequenz.
Die Frequenz und die Periodendauer können in einander umgerechnet werden. Dazu kann man die folgende Formel verwenden.
\(T=\)\(\frac{1}{f}\)
Bildet man den Kehrwert dieser Gleichung, so kommt man auf
\(f=\)\(\frac{1}{T}\)
Anhand dieser zwei Formeln sieht man, dass die Frequenz und Periodendauer in einem antiproportionalem Verhältniss zu einander stehen.
