Die elektrische Ladung
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
elektrische Ladung
Was ist eine elektrische Ladung und wie kann man sie berechnen? In diesem Beitrag findest du alles wichtige über die Einheit und Formeln zu der elektrischen Ladung. Am besten du schaust dir auch das Video an.
Was ist elektrische Ladung?
Um ein Verständnis für die elektrische Ladung zu entwickeln, müssen wir uns zunächst mit dem Aufbau eines Atoms beschäftigen. In unserer Modellvorstellung besteht ein Atom aus einer Atomhülle, in dieser Atomhülle befinden sich negativ geladene Elektronen. Im Atomkern hingegen befinden sich die positiv geladenen Protonen und die neutralen Neutronen.
Im "Normalfall" sind die meisten Stoffe nicht geladen, man sagt, der Stoff ist elektrisch neutral. Ein elektrisch neutraler Stoff besitzt gleich viele Elektronen wie Protonen, ihre Ladungen gleichen sich daher aus. Besitzt ein Stoff mehr Elektronen als Protonen so ist er negativ geladen, man spricht von einem Elektronenüberschuss. Umgekehrt ist ein Stoff positiv geladen wenn er mehr Protonen als Elektronen besitzt, man spricht dann von einem Elektronenmangel.
Elektrische Ladung Einheit
Ein Elektron besitzt die kleinste elektrische Ladung die es gibt. Die Einheit der elektrischen Ladung ist Coulomb, das Formelzeichen der Ladung ist \(C\). Man nennt die Ladung eines Elektrons Elementarladung.
Elementarladung
\(e=1,602\cdot 10^{-19}C\)
Ein Elektron bestizt die Ladung \(-e\) da ein Elektron negativ geladen ist.
Ein Proton bestizt die Ladung \(+e\) da ein Proton positiv geladen ist.
Achtung !
Warum ein Elektron die Ladung \(-e=-1,602\cdot 10^{-19}C\) besitzt und woher diese Ladung stammt ist der Physik noch ein Rätsel. Daher sagt man auch, "die Ladung ist eine intrinsisch Eigenschaft".
Die elektrische Ladung eines Objekts gibt an, wie positiv oder negativ das Objekt geladen ist.
Elektrische Ladung Einheit und Formelzeichen
Formelzeichen: Q oder q
Einheit: C (Coulomb) bzw. As (Amperesekunde)
Elektrische Ladung Formel
Man kann die Formel der elektrischen Ladung zum einen über die Elementarladung \(e\) und zum anderen über die Stromstärke angeben.
Formel über die Stromstärke
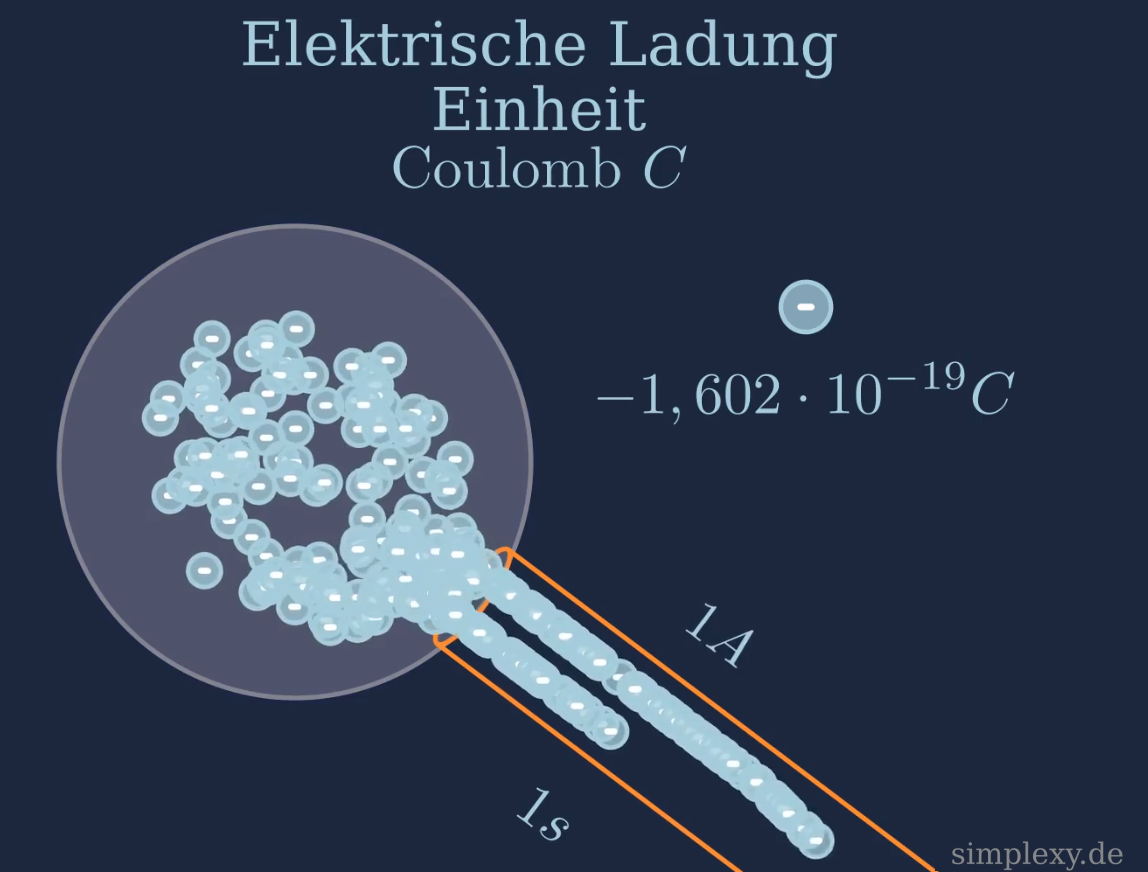
Ein Coulomb ist die Ladung, die durch den Querschnitt eines Drahts transportiert wird, wenn für 1 Sekunde eine Stromstärke von 1 Ampere fließt.
Coulomb
\(1C=1A\cdot s\)
Formel über die Elementarladung

Weis man wie groß der Elektronenüberschuss eines Körpers ist, so kann man über die folgende Formel die Gesamtladung des Körpers berechnen.
Gesamteladung eines Körpers
\(C=k\cdot e\)
Dabei ist \(e=1,602\cdot 10^{-19}C\) die Elementarladung und \(k\) der Elektronenüberschuss bzw. Elektronenmangel.
Elektrische Ladung berechnen
Beispiel:
Ein Ballon besitzt eine negative Ladung von \(2,5 C\). Wie hoch ist der Elektronenüberschuss?
Lösung:
\(\begin{aligned} Q&=2,5C\\ \\ e&=1,602\cdot 10^{-19}C\\ \\ Q&=n\cdot e\\ \\ &\implies\\ \\ n&=\frac{Q}{e}=\frac{2,5C}{1,602\cdot 10^{-19}C}\\ \\ &=1,5605\cdot 10^{19}\\ \\ \end{aligned}\)
Der Ballon hat einen Elektronenüberschuss von \(1,5605\cdot 10^{19}\) Elektronen
Elektrische Ladung und Stromstärke
In dem letzten Abschnitt haben wir die Definition der Einheit Coulomb erläutert. Fließt durch einen Leiter für 1 Sekunde eine Stromstärke von 1 Ampere, dann wird innerhalb dieser Sekunde eine Ladung von 1 Coulumb transportiert.
Dem zufolge hängt die Ladung auch von der Stromstärke ab. Je höher die Stromstärke ist, desto mehr Ladung wird in der gleichen Zeit transportiert. Der Zusammenhang zwischen der Stromstärke und der Ladung lässt sich wie folgt beschreiben:
Stromstärke, Ladung und Zeit
\(\begin{aligned} I=\frac{Q}{t} \end{aligned}\)
Dabei ist \(I\) die Stromstärke, \(Q\) die Ladung und \(t\) die Zeit.
Die Stromstärke gibt einem an wie viel Ladung pro Zeit durch den Querschnitt eines Drahts fließt.
Beispiel Ladung über die Stromstärke berechnen
Durch ein Draht fließt für eine halbe Stunde ein Strom mit der Stromstärke von \(2A\). Wie groß ist die gesamte Ladung die in dieser Zeit durch den Draht transportiert wurde ?
Lösung:
\(\begin{aligned} I&=2A\\ \\ t&=30\,min=1800\,s\\ \\ I&=\frac{Q}{t}\,\,\,\,\,\,\,|\cdot t\\ \\ Q&=I\cdot t\\ \\ Q&=2A\cdot 1800s=3600C\\ \\ \end{aligned}\)
In einer halben Stunde fließt durch den Draht eine Gesamtladung von \(3600\) Coulomb.
Ladungstrennung
Wie bereits erwähnt sind Objekte in der Regel elektrisch neutral. Durch Reibung können elektrische Ladungen jedoch getrennt werden. Dabei übertragen sich einige Ladungsträger von dem einen Objekte zum anderen. Hört man mit der Reibung auf, so erhält man zwei elektrisch geladene Körper.
Dieses Verhalten kann man bei einem Luftballon den man am Kopf reibt beobachten. Sobald man den Luftballon an den Haaren reibt, wandern Elektronen (negative Ladung) von den Haaren in das Gummi vom Ballon. Der Elektronenmangel in den Haaren führt dort zu einer positiven Ladung. Der Ballon hat jedoch einen Elektronenüberschuss und ist damit negativ geladen.
Das sich entgegengesetzte Ladungen anziehen, kann man daran erkennen, das die Haare von der Oberfläche des Ballons angezogen werden. Ist der Ballon nicht mehr in der Nähe der Haare, kann man beobachten, wie sich die Haare gegenseitig abstoßen. Die Haare stehen einem zu Berge, weil sich gleiche Ladungen abstoßen.
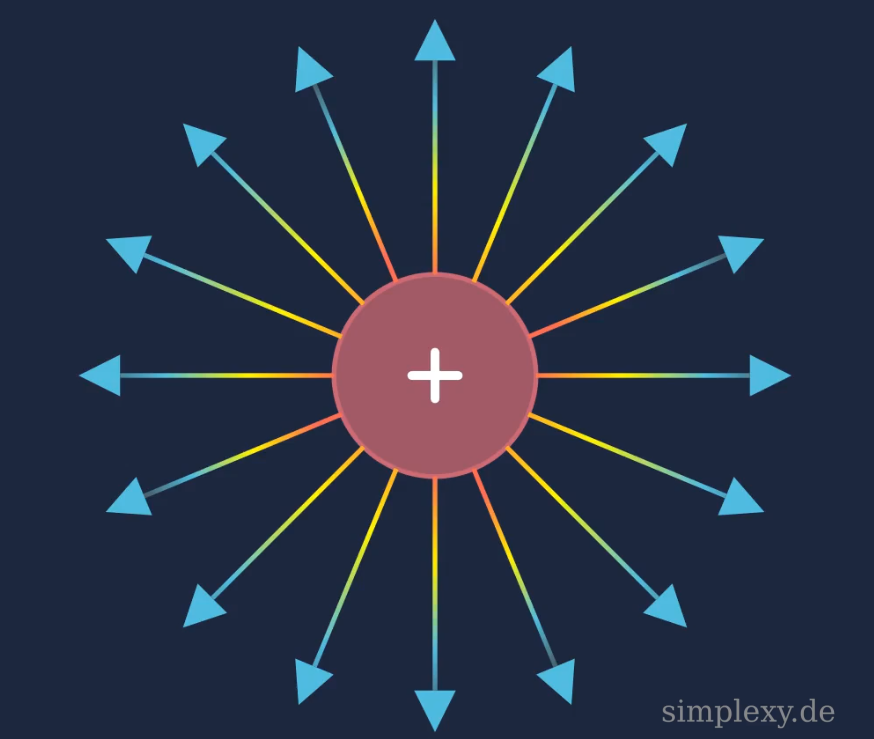
Elektrisches Feld von Ladungen
Jede elektrische Ladung besitzt ein elektrisches Feld. Um ein elektrisch geladener Körper entsteht ein elektrisches Feld mit sogenannten Feldlinien. Die elektrischen Felder von geladenen Körper führen zu den Wechselwirkungen (Anziehung und Abstoßung) zwischen den geladenen Körper.
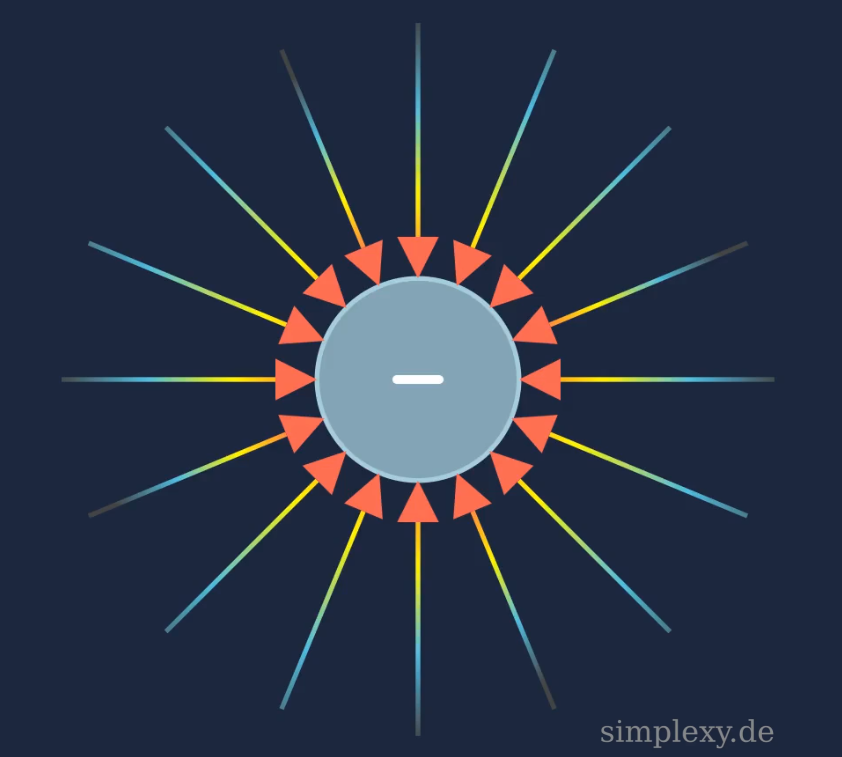
Das elektrische Feld einer negativen Punktladung verläuft überall radial und ist zum Zentrum der Ladung gerichtet.
Das elektrische Feld einer positiven Punktladung ist ebenfalls überall Radial, das Feld ist jedoch vom Zentrum der Ladung nach außen gerichtet.