Exponentialfunktion
Exponentialfunktion Rechner
Mit dem Online Rechner von Simplexy kannst du viele Matheaufgaben lösen und gleichzeitig den Lösungsweg erhalten.
Grundlagen der Exponentialfunktion
Die Exponentialfunktion ist wie der Name bereits sagt, eine Funktion bei dem der Exponent eine besondere Rolle einnimmt. In dem Beitrag zu den Potenzfunktionen lernst du wie man mit Funktionen der Form \(f(x)=x^n\) umgeht, hier ist der Exponent \(n\) eine Konstante und die Variable \(x\) ist die Basis.
Bei der Exponentialfunktion liegt die Besonderheit hingegen darin, dass die Variable \(x\) im Exponenten steht.
Beispiele dafür sind:
Beispiel:
- \(f(x)=2^x\)
- \(f(x)=4^{x-3}\)
- \(f(x)=\frac{1}{2}^x\)
Eigenschaften der Exponentialfunktion
Die allgemeine Funktionsgleichung der Exponentialfunktion sieht wie folgt aus:
\(f(x)=a^x\)
Die Variable \(x\) steht im Exponenten und \(a\) ist eine Konstante die man Basis nennt. Die Basis \(a\) muss eine positive reelle Zahl sein. Bei den Exponentialfunktionen unterscheidet man zwischen zwei Arten:
- Exponentialfunktionen mit \(a\gt 1\)
- Exponentialfunktionen mit \(0\lt a\lt 1\)
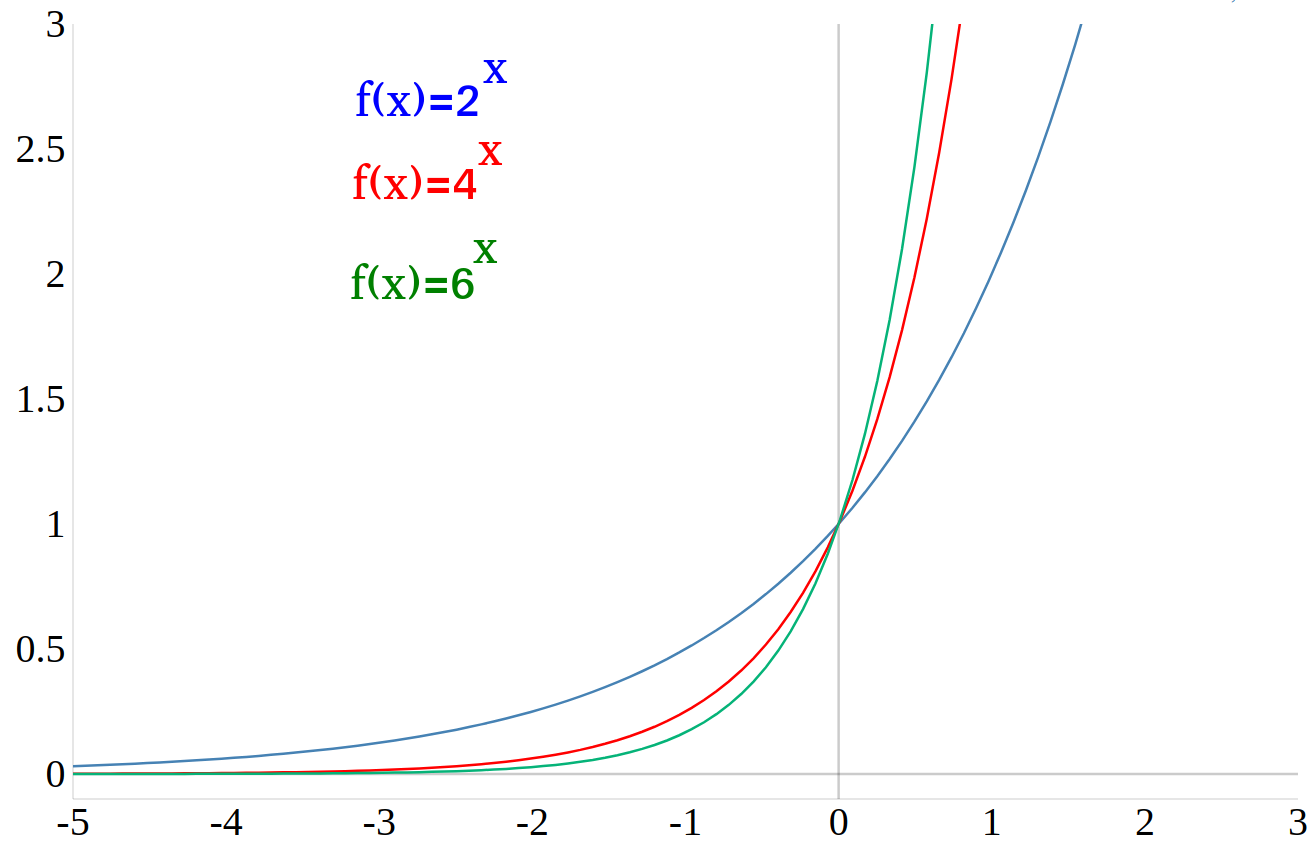
Exponentialfunktionen mit \(a\gt 1\)
Ist die Basis der Exponentialfunktion größer als \(1\), dann ist die Funktion streng monoton wachsend. Je größer \(a\) ist, desto steiler verläuft der Graph.
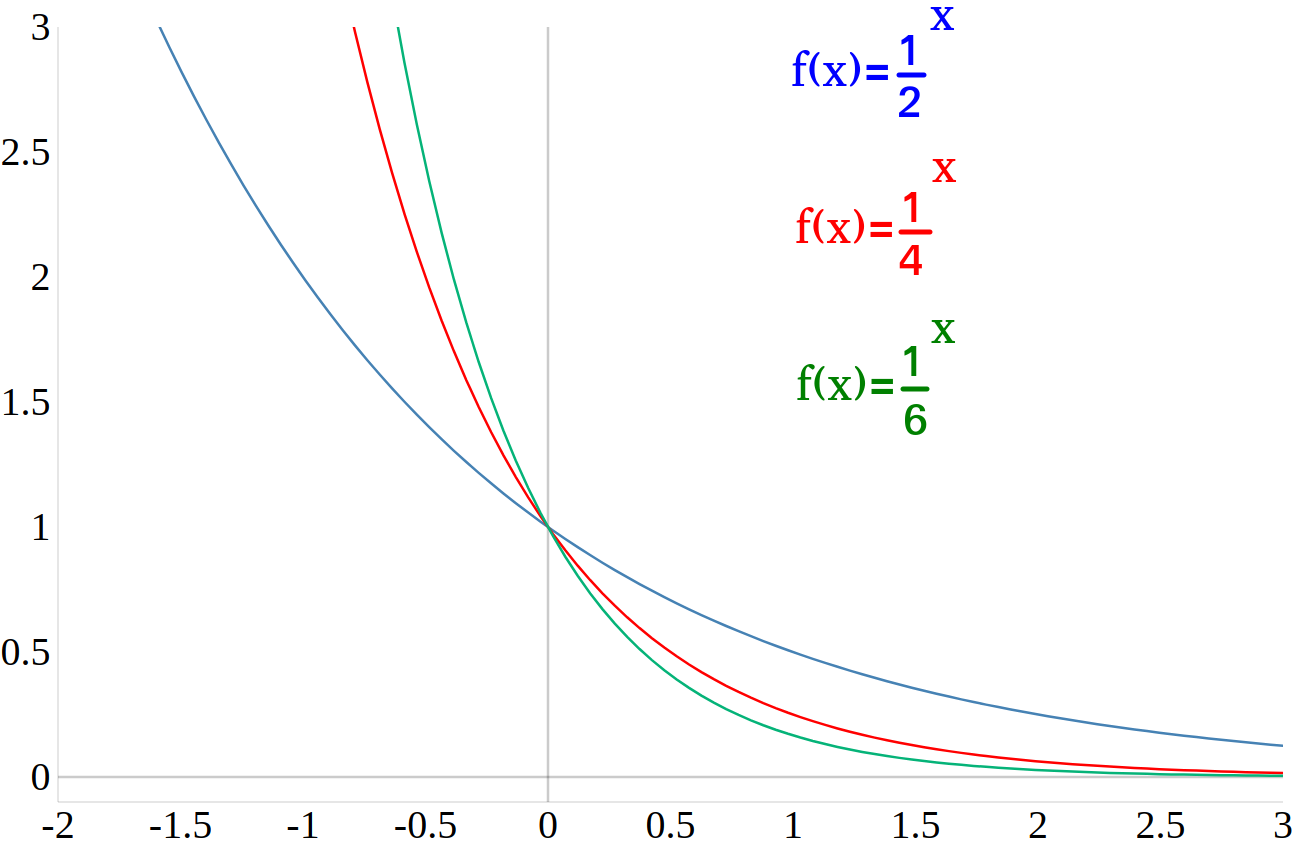
Exponentialfunktionen mit \(0 \lt a\lt 1\)
Ist die Basis der Exponentialfunktion zwischen Null und Eins, dann ist die Funktion streng monoton fallend. Je kleiner \(a\) ist, desto steiler verläuft der Graph.
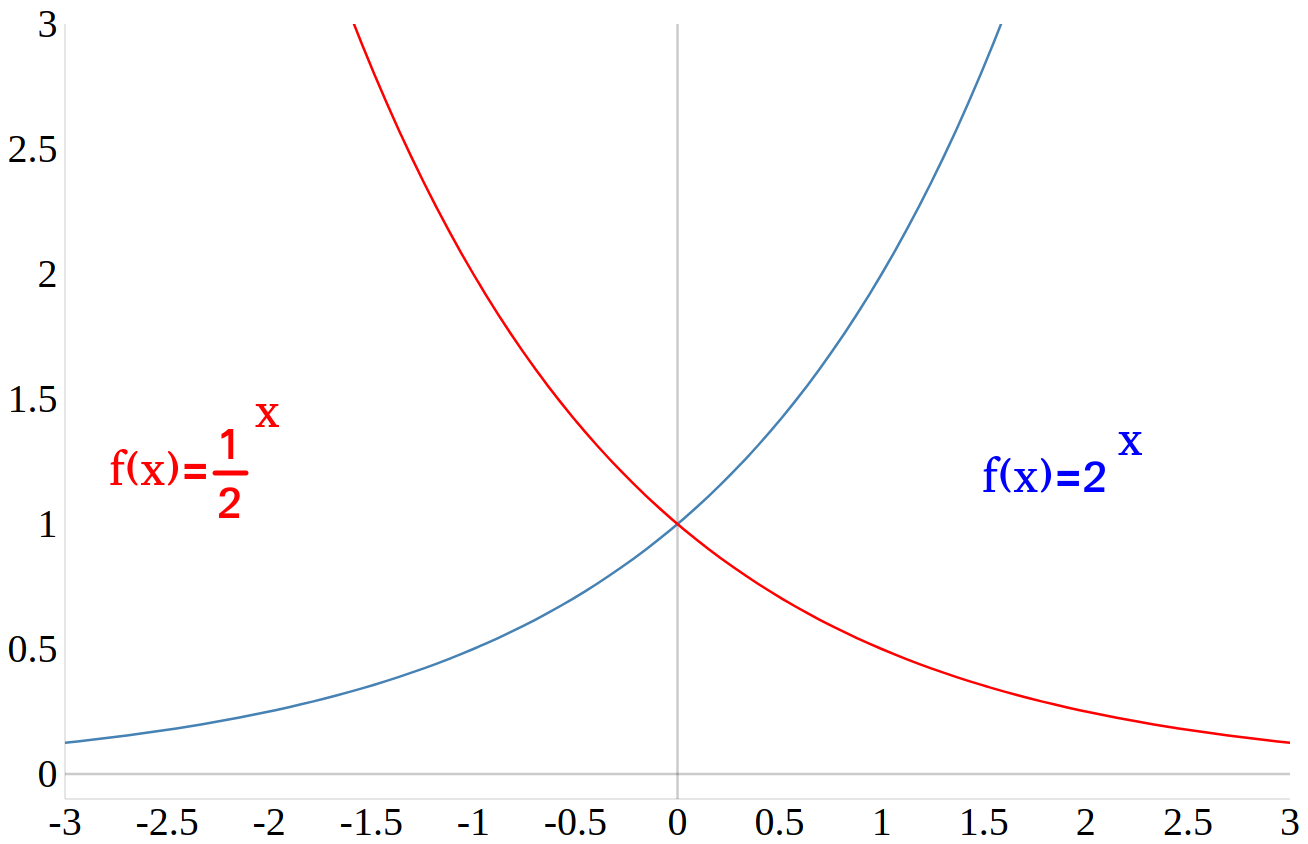
Besonderheiten der Exponentialfunktionen
Womöglich ist es dir schon aufgefallen, die Funktionsgraphen von \(\frac{1}{2}^x\) und \(2^x\) werden durch eine Spiegelung an der \(y\)-Achse aufeinander abgebildet. Das gilt natürlich auch im Allgemeinen für \(a^x\) und \(\frac{1}{a}^x\).
Regel:
Für alle Exponentialfunktionen der Form \(f(x)=a^x\) gilt:
- Die Funktion hat keine Nullstellen.
- Der Graph der Funktion besitzt kein Symmetrieverhalten.
- Der Funktionsgraph geht durch den Punkt \(P(0|1)\).
- Für \(a\gt 1\) ist die Funktion streng monoton steigend.
- Für \(0\lt a\lt 1\) ist die Funktion streng monoton fallend.
- Die \(x\)-Achse ist Asymptote für den Graphen.
Streckung und Spiegelung
der Exponentialfunktion
Wenn man die Funktionsgleichung der Exponentialfunktion mit einer Konstante multipliziert, dann kann man den Graphen strecken und an der \(x\)-Achse spiegeln. Die Funktionsgleichung lautet wie Folgt:
\(f(x)=b\cdot a^x\)
Mit dem Steckungsfaktor b wird bewirkt, dass der Graph parallel zur \(y\)-Achse gestreckt wird. Ist der Steckungsfaktor negativ, dann wird der Graph zusätzlich noch an der \(x\)-Achse gespiegelt.
Beispiel
Betrachten wir mal die Funktion \(f(x)=2^x\).
Wir strecken die Funktion \(f(x)\) mit dem Streckungsfaktor \(3\) und erhalten die Funktion
\(g(x)=3\cdot 2^x\)
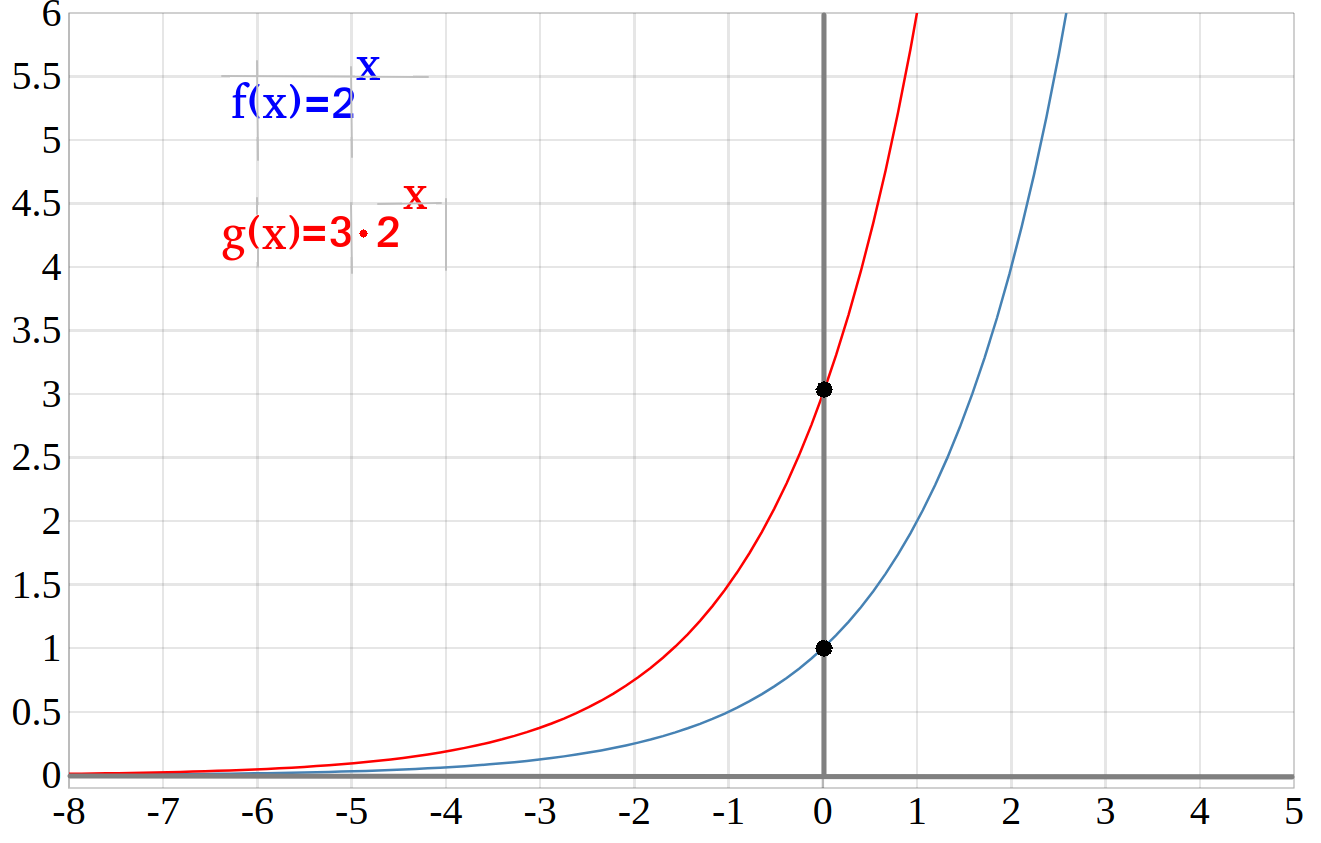
Wie man sieht, ist die Funktion \(g(x)\) steiler als die Funktion \(f(x)\) zusätzlich schneidet die Funktion \(g(x)\) die \(x\)-Achse am Punkt \(P(0|3)\)
Eine Spiegelung entlang der \(x\)-Achse erhält man, mit einem negativen Streckungsfaktor. Betrachten wir dazu zum Beispiel die Funktion
\(h(x)=-3\cdot 2^x\)
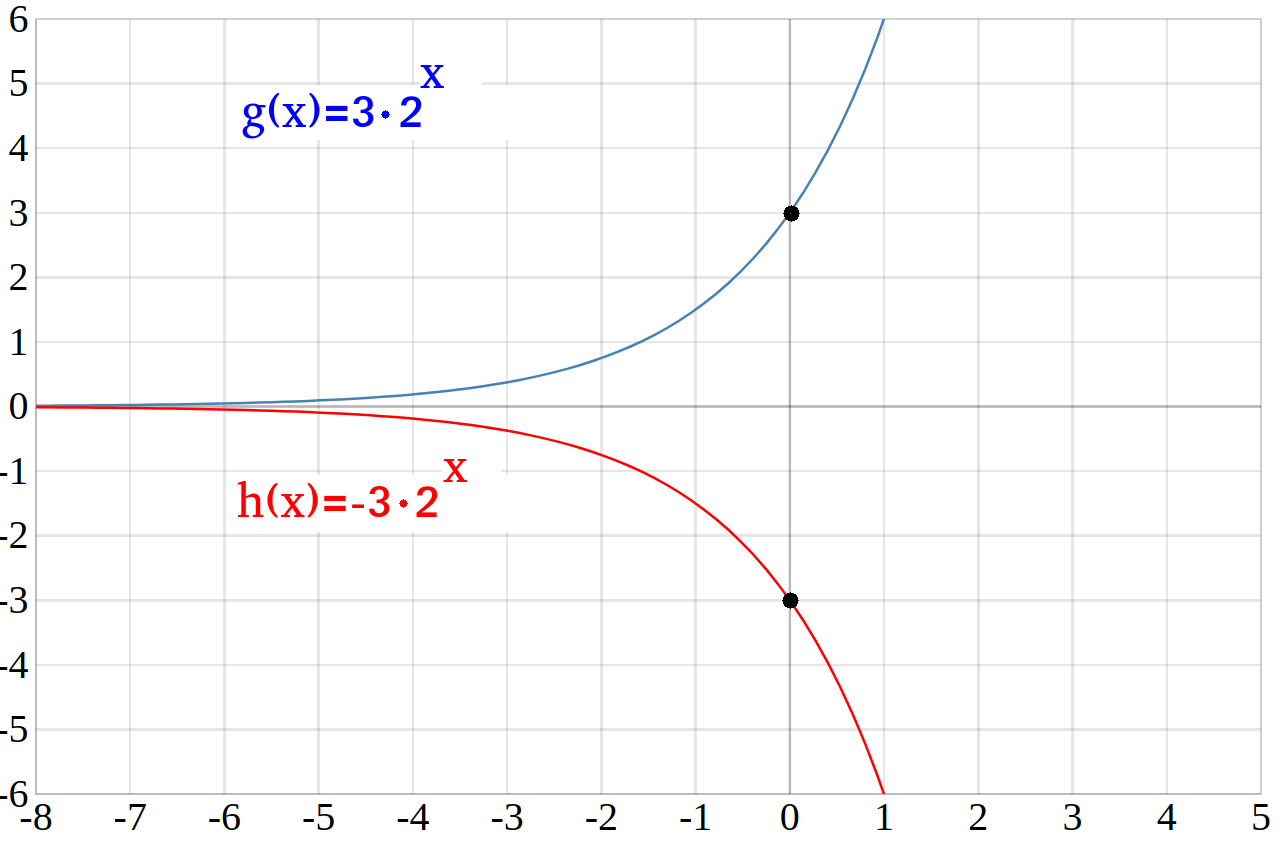
Wie man sieht führt ein negativer Streckungsfaktor zu einer Spiegelung an der \(x\)-Achse.
Eine Exponentialfunktion kann natürlich auch mit einem Streckungsfaktor zwischen \(0\) und \(1\) multipliziert werden. In so einem Fall würde der Graph flacher verlaufen. Nehmen wir als Beispiel die Funktionen
\(i(x)=\frac{1}{2}\cdot 2^x\) und
\(l(x)=-\frac{1}{2}\cdot 2^x\)
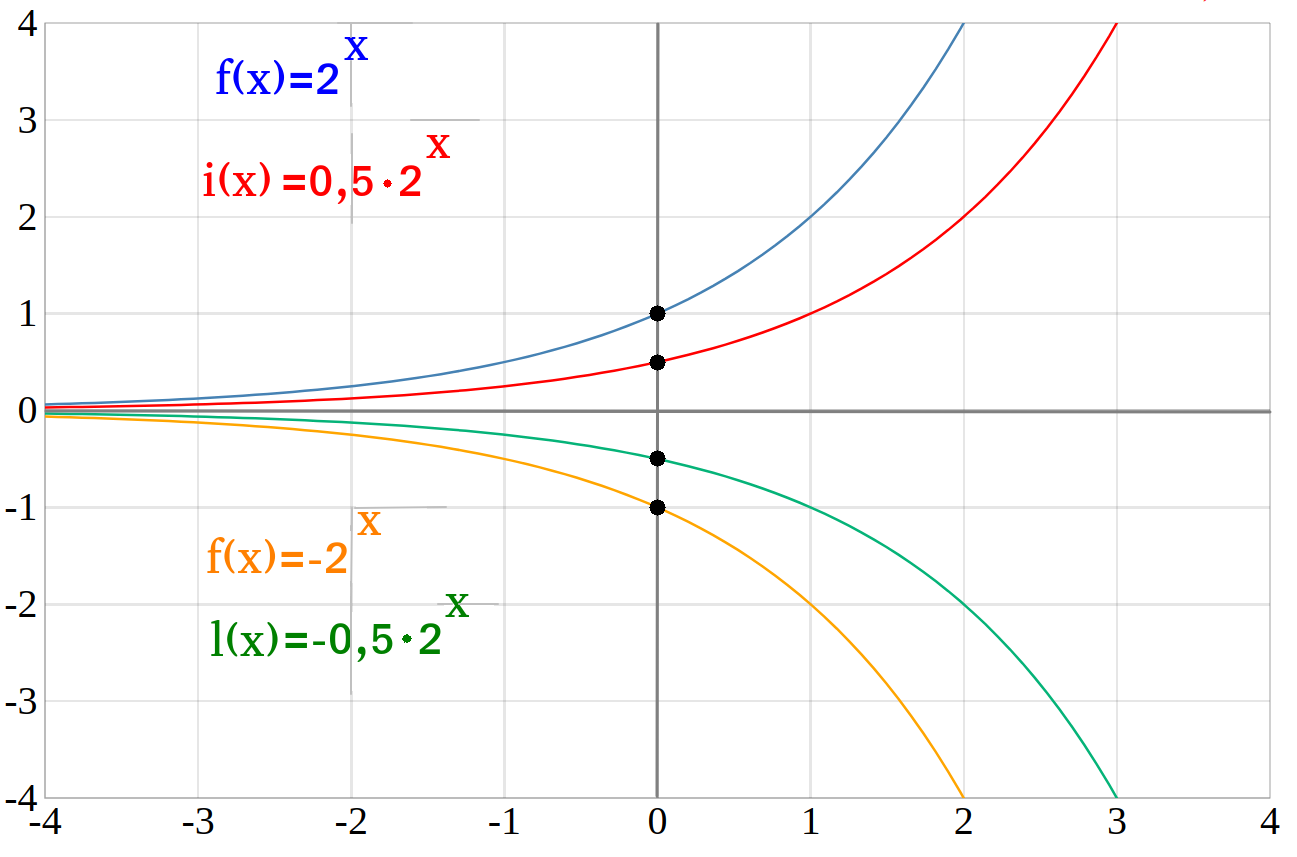
Verschiebung entlang der \(x\)-Achse
Eine Exponentialfunktion lässt sich mit einer Verschiebungskonstante \(c\) entlang der \(x\)-Achse verschieben. Wenn \(c\) positiv ist, dann erfolgt die Verschiebung um \(c\) Einheiten nach Links. Ist \(c\) jedoch negativ dann wird der Graph um \(c\) Einheiten nach Rechts verschoben.
Man schreibt die Funktion dann wie folgt:
\(f(x)=a^{x+c}\)
Beispiele
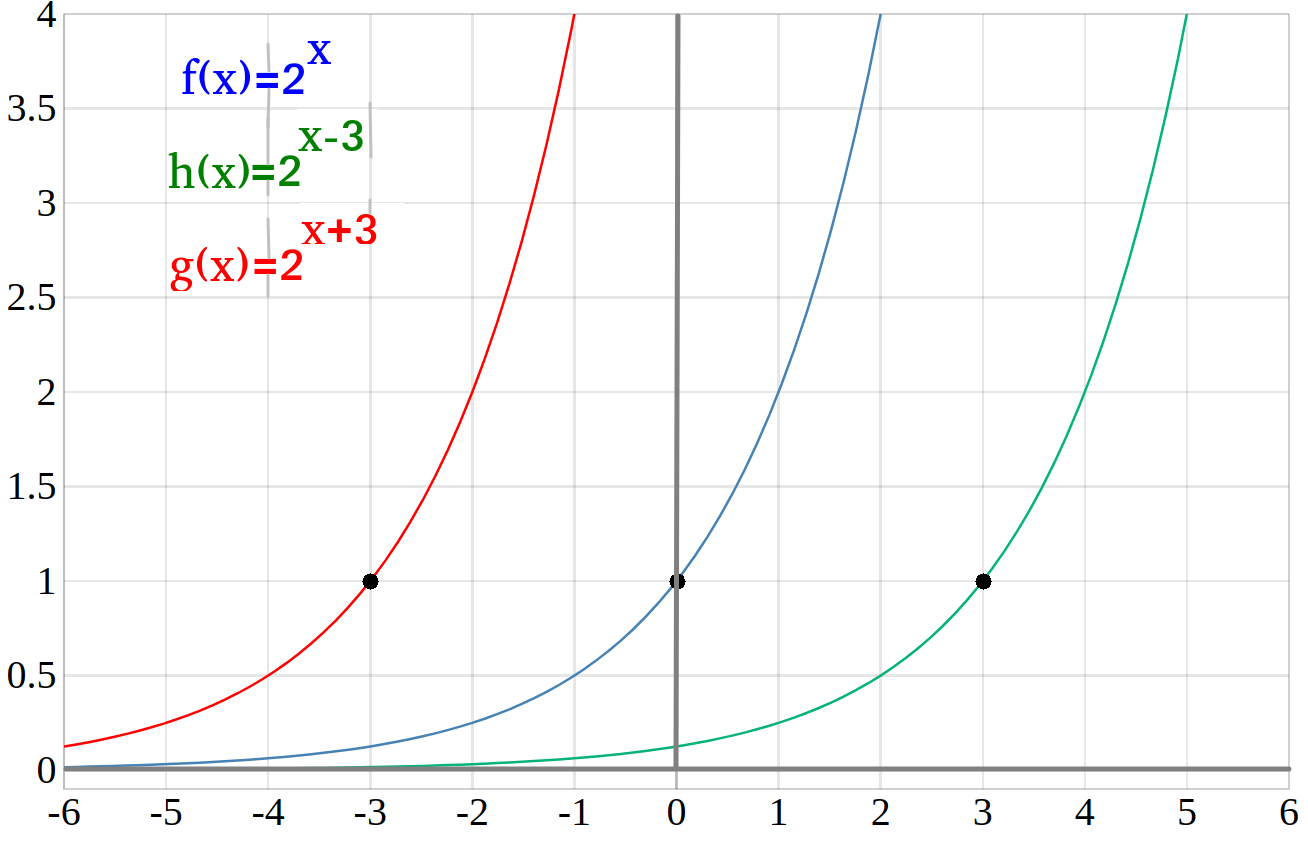
- \(f(x)=2^x\)
- \(h(x)=2^{x-3}\)
- \(g(x)=2^{x+3}\)
Verschiebung entlang der \(y\)-Achse
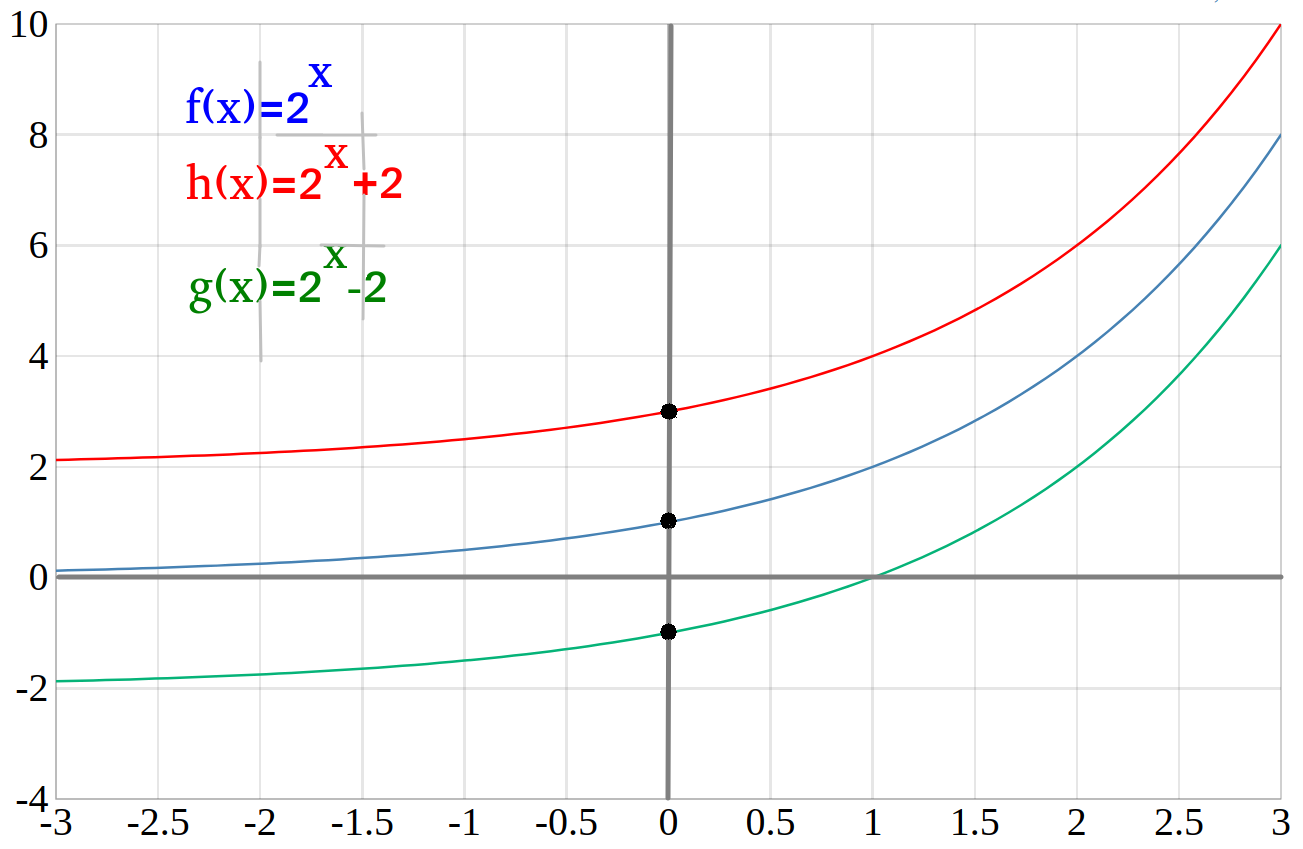
Eine Verschiebung entlang der \(y\)-Achse kann man mit Hilfe der Verschiebungskonstante \(d\) hervorrufen. Wenn \(d\) positiv ist, dann wird der Graph nach Oben verschoben. Ist \(d\) jedoch negativ, dann erfolgt die Verschiebung nach Unten.
Allgemein schreibt man die Funktion mit dem Verschiebungfaktor wie folgt:
\(f(x)=a^x+d\)
Beispiele
- \(f(x)=2^x\)
- \(h(x)=2^{x}+2\)
- \(g(x)=2^{x}-2\)