Monotonieverhalten einer Funktion
Online Rechner
Der Online Rechner von Simplexy kann dir beim Monotonie Verhalten einer Funktion helfen. Mit dem Rechner kannst du dir den Graphen einer Funktion zeichnen lassen, die Funktion ableiten und viel mehr.
Monotonieverhalten
Das Monotonieverhalten einer Funktion ist ein wichtiger Bestandteil einer Kurvendiskussion. Um die Montonie einer Funktion zu ermitteln muss man sich fragen ob die Funktion steigt oder fällt. In dem unteren Video findest du eine kurze Einleitung zum Thema Monotonieverhalten einer Funktion.
Um eine Aussage über das Monotonieverhalten einer Funktion zu treffen muss man sich mit der Steigung der Funktion beschäftigen. Die Steigung einer Funktion lässt sich mit der ersten Ableitung \(f'(x)\) berechnen:
Monotonieverhalten bestimmen
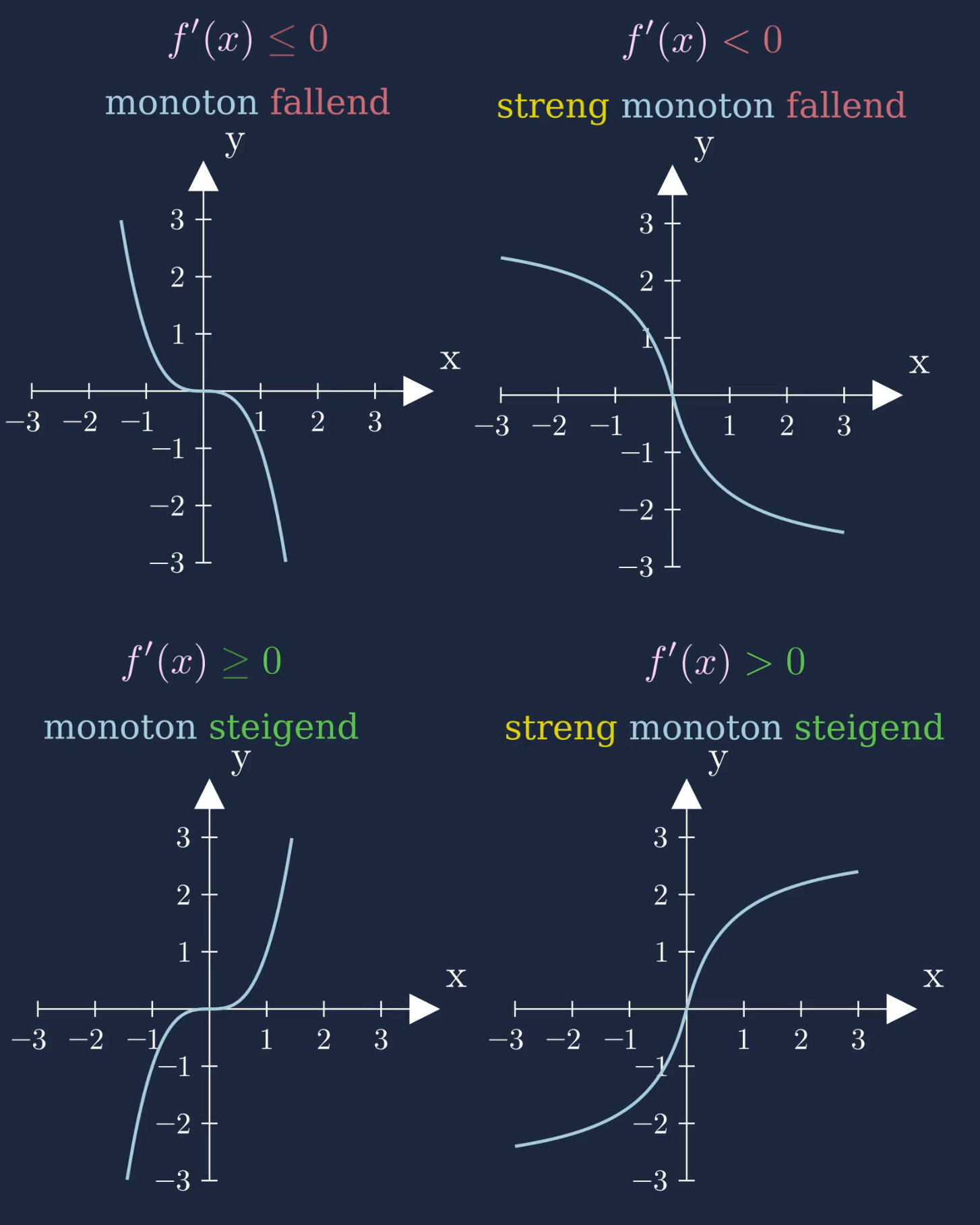
- \(f'(x)\geq 0 \,\,\,\implies\,\,\,f(x)\) ist monoton steigend
- \(f'(x)\leq 0 \,\,\,\implies\,\,\,f(x)\) ist monoton fallend
- \(f'(x)\gt 0 \,\,\,\implies\,\,\,f(x)\) ist streng monoton steigend
- \(f'(x)\lt 0 \,\,\,\implies\,\,\,f(x)\) ist streng monoton fallend
Achtung !
Der unterscheid zwischen monoton und streng monoton ist wichtig.
Streng monoton bedeutet, dass die Steigungsfunktion \(f'(x)\) für alle \(x\)-Werte größer (oder kleiner) als Null ist.
Monotonieverhalten in verschiedenen Intervallen
Wie wir in dem oberen Video bereits gesehen haben, kann eine Funktion in verschiedenen Bereichen unterschiedliche Monotonieverhalten besitzen. Eine Funktion kann in einigen Bereichen steigen und in anderen Bereichen fallen. In solchen Fällen muss man die Funktion in Intervalle unterteilen.
An den Extrempunkten einer Funktion, ändert sich das Monotonieverhalten. Die Intervallgrenzen werden durch die Extrempunkte bestimmt.
Um das Monotonieverhalten von Funktion zu untersuchen, die sowohl fallende als auch steigende Bereiche besitzen, muss man zunächst die Einteilung der Funktion vornehmen. Man unterteilt die Funktion in lediglich steigende und ledigleich fallende Bereiche. Die jeweiligen Intervalle werden durch die Extrempunkte abgerenzt.
Monotonieverhalten bestimmen
- \(f'(x)\) berechnen
- \(f'(x)=0\) setzen und die Nullstellen der Ableitung berechnen (Extrempunkte berechnen).
- Intervalle aufschreiben.
- In jedem Intervall ein \(x\)-Wert aussuchen und in \(f'(x)\) einsetzen. Das Vorzeichen gibt die Steigung in dem jeweiligen Intervall an.
Beispiel Montonie
Untersuche die folgende Funktion auf das Monotonieverhalten:
\(f(x)=x^3-3x^2+3\)
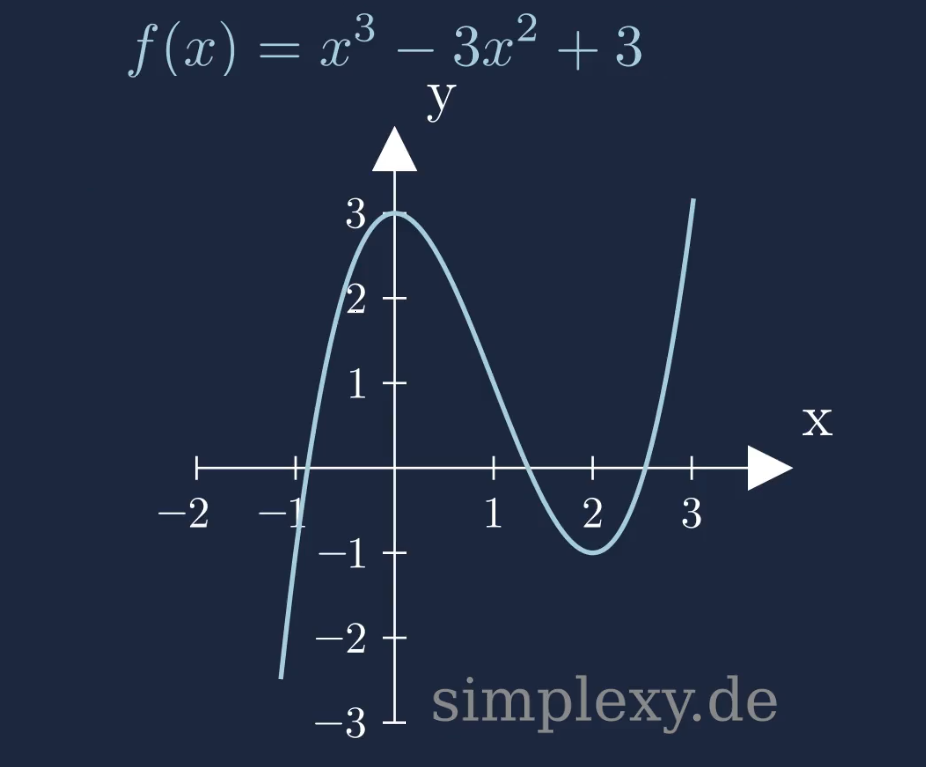
In diesem Fall besitzt die Funktion keine eindeutige Monotonie. Daher muss die Funktion in Intervalle eingeteilt werden, in denen das Monotonieverhalten separat untersucht werden kann. Die Intervalle werden durch die Extrempunkte abgegrenzt. Wir müssen daher zunächst die Extrempunkte der Funktion berechnen. Dazu wird die Ableitung der Funktion nullgesetzt:
\(\begin{aligned} f'(x)=&\,\,3x^2-6x=0\\ &\implies\\ \textcolor{green}{x_1=}&\,\,\textcolor{green}{0}\,\,\,\,\,\,\textcolor{red}{x_2=2}\\ \end{aligned}\)
Wir wissen nun das der Hochpunkt bei \(\textcolor{green}{x_1=0}\) und der Tiefpunkt bei \(\textcolor{red}{x_2=2}\) liegt
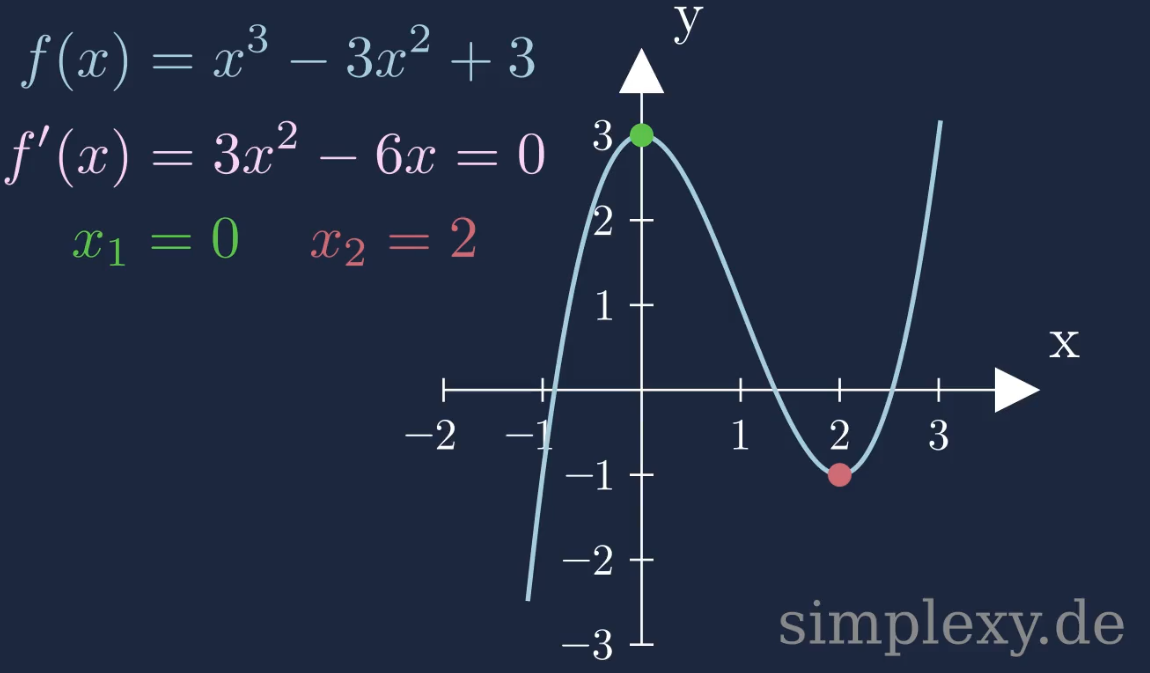
An den Extrempunkten ändert sich das Monotonieverhalten einer Funktion. An einem Hochpunkt geht eine Funktion von einer Steigung in ein Gefälle über. An einem Tiefpunkt geht eine Funktion von einem Gefälle in eine Steigung über. Wir können nun die Einteilung der Funktion in drei Intervalle vornehem.
\(\begin{aligned} I_1&:(-\infty|\textcolor{green}{0})\\ I_2&:(\textcolor{green}{0}|\textcolor{red}{2})\\ I_3&:(\textcolor{red}{2}|\infty)\\ \end{aligned}\)
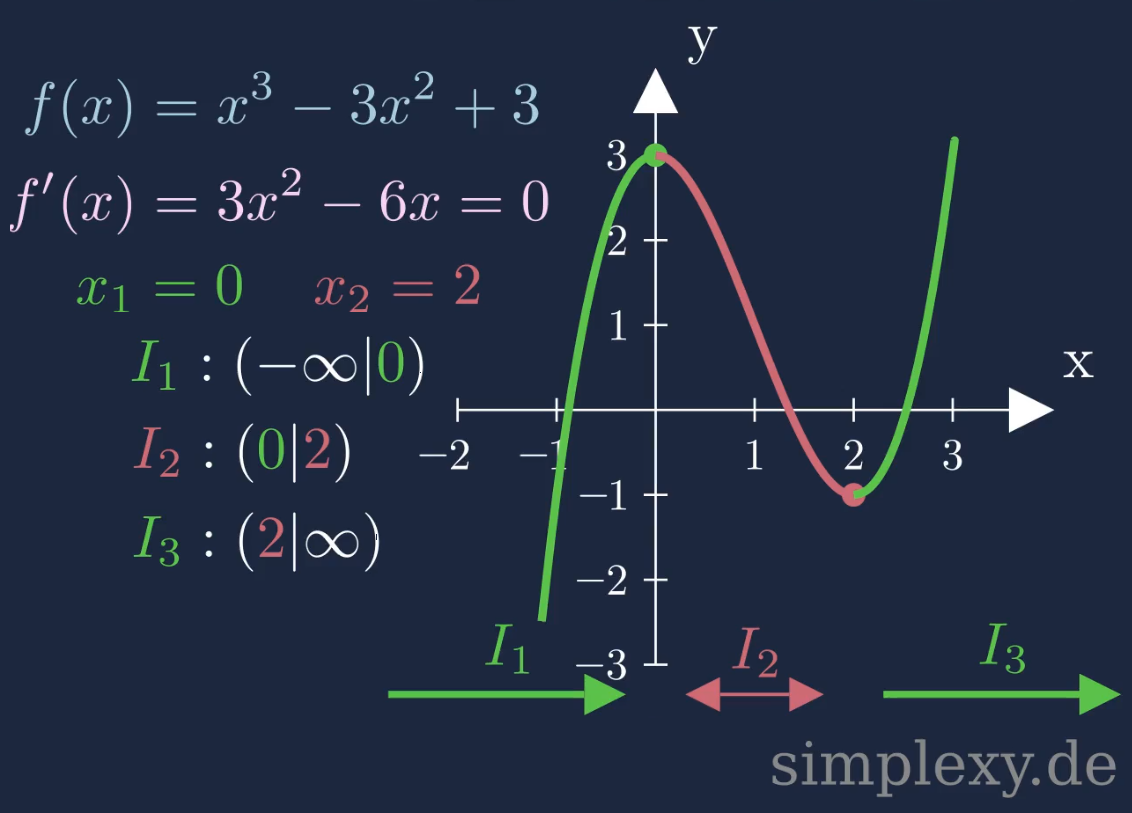
Nun ist die Funktion in drei Intervalle eingeteilt worden. Wir müssen nun rausfinden, welche Monotonie in den jeweiligen intervallen vorliegt. Dazu muss man aus jedem Intervall ein \(x\)-Wert in die erste Ableitung \(f'(x)\) einsetzen. Wenn dabei ein positiver Wert raus kommt, so steigt die Funktion in diesem Intervall. Erhält man jedoch einen negativen Wert, so fällt die Funktion in diesem Intervall.
Der \(x\)-Wert \(\textcolor{blue}{x=-1}\) liegt im ersten Intervall \(I_1\) und wird nun in \(f'(x)\) eingesetzt um die Monotonie im ersten Intervall zu ermitteln.
\(\begin{aligned} f'(\textcolor{blue}{-1})&=3\cdot (\textcolor{blue}{-1})^2-6\cdot (\textcolor{blue}{-1})\\ &=\textcolor{green}{9}>0 \end{aligned}\)
Wir sehen nun, dass \(f'(\textcolor{blue}{-1})\) größer als Null ist. Damit ist die Funktion im ersten Intervall streng monoton steigend.
Als nächstes setzen wir den \(x\)-Wert \(\textcolor{blue}{x=1}\) aus dem zweiten Intervall in \(f'(x)\) ein.
\(\begin{aligned} f'(\textcolor{blue}{-1})&=3\cdot (\textcolor{blue}{1})^2-6\cdot (\textcolor{blue}{1})\\ &=\textcolor{red}{-3}< 0 \end{aligned}\)
Im zweiten Intervall ist \(f'(\textcolor{blue}{-1})\) kleiner als Null, damit ist dort die Funktion streng monoton fallend.
Zuletzt setzen wir den \(x\)-Wert \(\textcolor{blue}{x=3}\) aus dem dritten Intervall in \(f'(x)\) ein.
\(\begin{aligned} f'(\textcolor{blue}{3})&=3\cdot (\textcolor{blue}{3})^2-6\cdot (\textcolor{blue}{3})\\ &=\textcolor{green}{9}> 0 \end{aligned}\)
Im dritte Intervall ist \(f'(\textcolor{blue}{3})\) größer als Null, damit ist dort die Funktion streng monoton steigend.
Zusammenfassend kann man sagen, dass die Funktion im Intervall
\(I_1\) streng monoton steigend ist.
\(I_2\) streng monoton fallend ist.
\(I_3\) streng monoton steigend ist.
