Differentialrechnung
Ableitungsrechner
Der Ableitungsrechner von Simplexy kann beliebige Funktionen für dich Ableiten und noch viel mehr. Um zum Beispiel die Funktion \(f(x)=x^2\) abzuleiten, geh auf den knopf \(\frac{df}{dx}\) und gib \(x^2\) ein. Dann kannst du auf lösen drücken und du erhälts die Ableitung deiner Funktion. Teste den Rechner aus.
Steigung einer Funktion - Differenzenquotient
Steigung einer Funktion berechnen
Mit Hilfe der Steigungsformel kannst du die Steigung einer Geraden berechnen. Man benötigt für eine Gerade lediglich zwei Punkte und aus denen kann man die Steigung der Geraden folgendermaßen berechnen:
\(m=\)\(\frac{y_2-y_1}{x_2-x_1}\)
wobei \(m\) die Steigung ist.
Wie sieht die Steigungsformel für eine beliebige Funktion aus?
Betrachten wir zwei beliebige Punkte einer Funktion \(f(x)\). Den ersten Punkt nennen wir
\(Q(x_1|f(x_1))\)
und den zweiten Punkt nennen wir
\(P(x_2|f(x_2))\)
Nun können wir die obige Formel für die Steigung \(m\) anwenden:
\(m=\)\(\frac{f(x_2)-f(x_1)}{x_2-x_1}\)
Dieser Bruch wird Differenzenqoutient gennant. Der Differenzenquotient liefert einem die Steigung der Geraden, die durch die Punkte \(Q\) und \(P\) verläuft. In der nächsten Abbildung siehst du eine beliebige Funktion \(f(x)\) und die Punkte \(Q\) und \(P\). Durch die zwei Punkte kann man eine Gerade zeichnen, die Steigung dieser Geraden lässt sich über den Differenzenqoutienten berechnen.
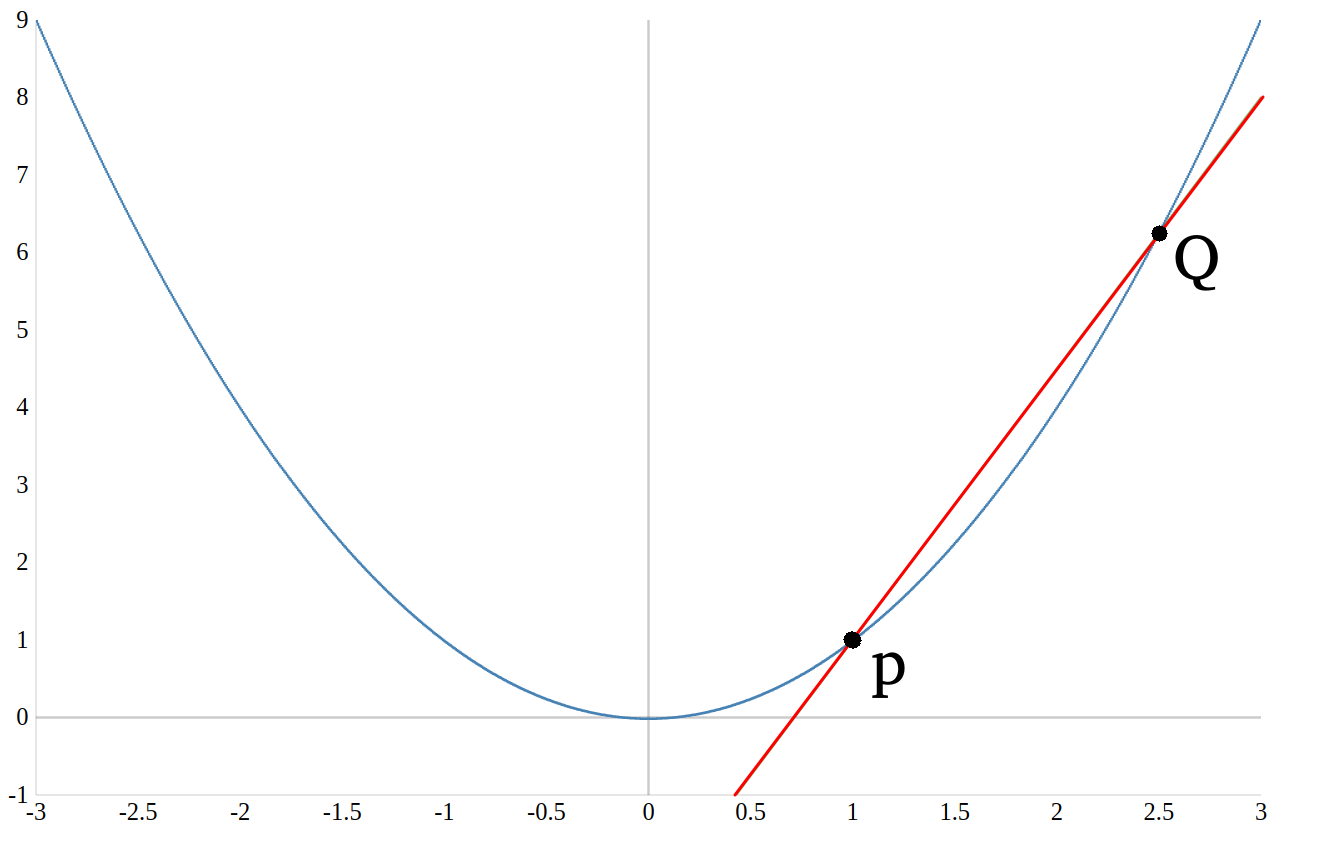
Mit dem Differenzenqoutient kann man also die Steigung einer Geraden berechnen die durch zwei Punkte einer beliebigen Funktion durchläuft. Wie kann man die Steigung einer Funktion an einem beliebigen Punkt berechnen?
Im nächsten Graph ist eine Funktion und ihrer Steigung am Punkt \(P\) dargestellt.
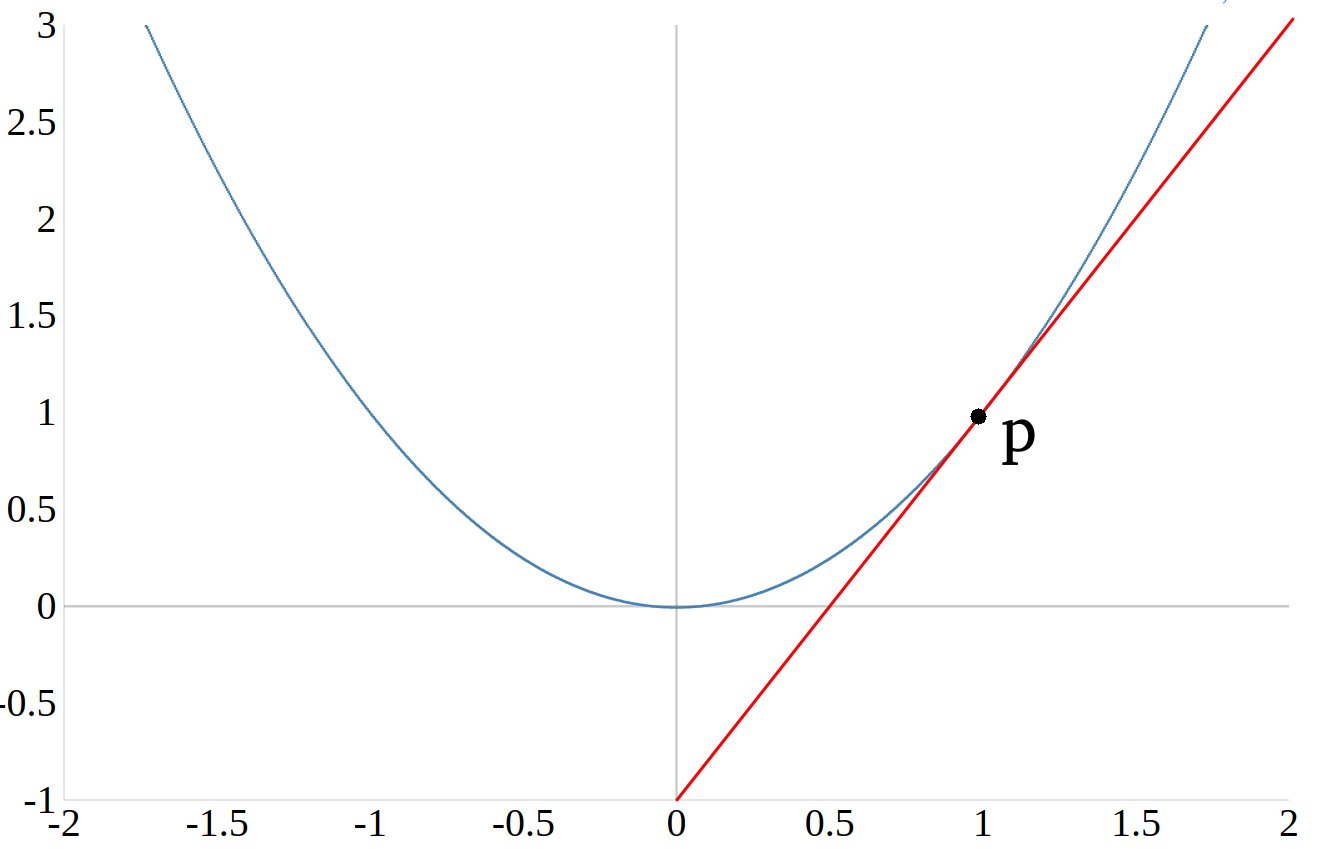
Doch wie erhält man die Steigung der Geraden an dem Punkt \(P\)?
Eine Möglichkeit mit der man die Gerade am Punkt \(P\) annähern kann besteht darin, wie in der ersten Abbildung dargestellt, zwei Punkte auf der Funktion zu wählen und den Abstand zwischen den zwei Punkten immer kleiner zu machen. Den Abstand machen wir kleiner, indem wir Punkt \(Q\) in Richtung Punkt \(P\) verscheiben.
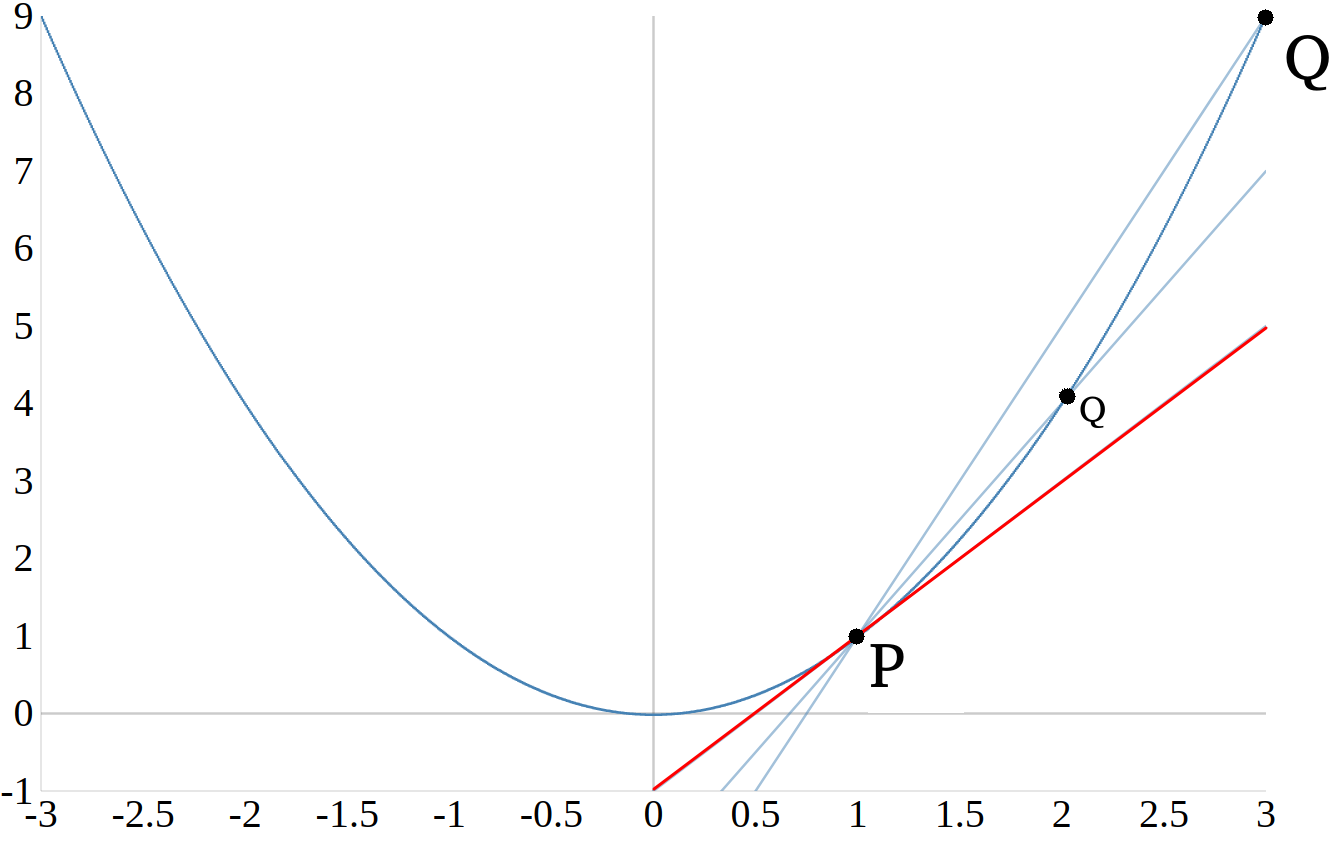
Wenn wir also Punkt \(Q\) immer näher an Punkt \(P\) schieben, so werden irgendwann die zwei Punkte zusammenfallen und die Gerade zwischen den zwei Punkten (Sekante) wird zu einer Geraden die nur noch den Punkt \(P\) berührt (Tangente).
Mathematisch lässt sich dies mit dem Limes (lim) ausdrucken.
\(m=\lim_{x_2 \to x_1}\)\(\frac{f(x_2)-f(x_1)}{x_2-x_1}\)
Dieser Ausdruck wird Differentialqoutienten gennant und dient dazu, die Steigung einer Funktion \(f(x)\) an der Stelle \(x_1\) zu berechnen.
Ableitungen
Die erste Ableitung einer Funktion \(f(x)\) an der Stelle \(x_0\) wird geschrieben als \(f'(x_0)\) oder \(\frac{df}{dx}|_{x_0}\). Die Steigung einer Funktion an der Stelle \(x_0\) entspricht der Steigung der Tangete an der Stelle \(x_0\). Wie in den Abbildungen oben gezeigt, kann an jeder Stelle der Funktion eine Tangente gelegt werden, deren Steigung entspricht \(f'(x_0)\). Mit der ersten Ableitung lässt sich neben der Steigung auch Aussagen über das Monotonie-Verhalten einer Funktion treffen. Zum Monotonie-Verhalten kommen wir später zurück, jetzt lernst du erstmal wie das Ableiten konkret funktioniert.
Ableitungsregeln
Das Ableiten mit dem Differentialqoutienten wird in der Praxis nicht gemacht, dazu ist der Rechenaufwand zu groß. Man verwendet zum Ableiten von Funktionen die sogenannten Ableitungsregeln, natürlich kann man diese Regeln herleiten bzw. beweisen. Für uns ist zunächst einmal das Anwenden der Ableitungregeln wichtig. Wendet man die Regeln richtig an, dann kann man jede Funktion die man in der Schule lernt ableiten.
Potenzregel
Die Potenzregel ist dafür da Funktionen der Form \(f(x)=x^n\) abzuleiten.
Regel:
Potenzregel
Ableitung von \(f(x)=x^n\)
\(f'(x)=n\cdot x^{n-1}\)
Dabei ist \(n\) eine beliebige Zahl.
Beispiele Potenzregel:
- \(\frac{d}{dx}\)\(x^3=3\cdot x^2\)
- \(\frac{d}{dx}\)\(x^2=2\cdot x\)
- \(\frac{d}{dx}\)\(x=1\)
- \(\frac{d}{dx}\)\(2\cdot x^3=6\cdot x^2\)
- \(\frac{d}{dz}\frac{1}{5}\)\(\cdot z^5=z^4\)
Mit dem Ableitungsrechner von Simplexy lassen sich Funktionen mit der Potenzregel ableiten.
Faktorregel
Die Faktorregel ist dafür da Funktionen der Form \(f(x)=c\cdot g(x)\) abzuleiten, dabei ist c eine Konstante.
Regel:
Faktorregel
Ableitung von \(f(x)=c\cdot g(x)\)
\(f'(x)=c.g'(x)\)
Dabei ist \(c\) eine konstante.
Beispiele Faktorregel:
- \(\frac{d}{dx}\)\(c\cdot x^4=4\cdot c\cdot x^3\)
- \(\frac{d}{dx}\)\(\alpha x^2=2\cdot \alpha \cdot x\)
- \(\frac{d}{dx}\)\(2\cdot x=2\)
Eine Funktion der Form \(f(x)=c\cdot g(x)\) ableiten ist sehr einfach. Da man eine Konstante \(c\) nicht ableiten kann, bzw. die Ableitung einer Konstante gleich Null ist, braucht man nur \(g(x)\) ableiten und die Konstante kann man ignorieren.
Der Ableitungsrechner von Simplexy ist in der Lage Funktionen mit der Faktorregel abzuleiten.
Summenregel
Die Summenregel ist dafür da Funktionen der Form
\(f(x)=g(x)\pm h(x)\) abzuleiten. Die Summenregel besagt, eine Funktion die durch eine Addition zweier Terme gebildet wird, leitet man ab indem man die einzel Terme ableitet und diese dann addiert .
Regel:
Summenregel
Ableitung von \(f(x)=g(x)\pm h(x)\)
\(f'(x)=g'(x)\pm h'(x)\)
Beispiele Summenregel:
- \(\frac{d}{dx}\)\((x^2+x)=2\cdot x+1\)
- \(\frac{d}{dx}\)\((2\cdot x^3+x^2)=6\cdot x^2 + 2\cdot x\)
- \(\frac{d}{dx}\)\((c\cdot x+\alpha x^2)=c+2\cdot \alpha\cdot x\)
Diese Regel ist sehr einfach anzuwenden. Wenn man eine Funktion als Summe zweier Terme schreiben kann, so leitet man diese Funktion ab, indem man die einzelnen Terme ableitet.
Mit dem Ableitungsrechner lassen sich Funktionen mittels Summenregel ableiten.
Produktregel
Die Produktregel sagt dir wie du Funktionen der Form
\(f(x)=g(x)\cdot h(x)\) abzuleiten hast. Eine Funktion die durch die Multiplikation zweier Terme zusammengesetzt ist leitet man folgendermaßen ab.
\(f'(x)=g'(x)\cdot h(x)+g(x)\cdot h'(x)\)
Regel:
Produktregel
Ableitung von \(f(x)=g(x)\cdot h(x)\)
\(f'(x)=g'(x)\cdot h(x)+g(x)\cdot h'(x)\)
Beispiele Produktregel:
\(\frac{d}{dx}\)\((5x^2-3x)\cdot 8x=(10x-3) \cdot 8x+(5x^2-3x)\cdot 8\)
\(\frac{d}{dx}\)\(\bigl((2\cdot x^3+x^2)\cdot x\bigr)=(6x^2+2x)\cdot x+(2x^3+x^2)\cdot 1\)
\(\frac{d}{dx}\)\(\bigl(c\cdot (x+\alpha x^2)\bigr)=\underbrace{0\cdot(x+\alpha x^2)}_{\text{=0}}+c\cdot (1+2\alpha x)\)
Eine Funktion ableiten, die sich aus dem Produkt zweier Terme schreiben lässt, ist ziemlich einfach. Man leitet zuerst den einen Term ab und multipliziert diese Ableitung mit dem zweiten Term. Im Anschluss leitet man den zweiten Term ab und multipliziert diese Ableitung mit dem ersten Term. Die Ergebnisse aus diesen zwei Schritten werden addiert.
Der Ableitungsrechner kann auch Funktionen mit der Produktregel ableiten. Probiere den Ableitungsrechner aus...
Kettenregel
Die Kettenregel sagt dir wie du Funktionen der Form
\(f(x)=g\bigl(h(x)\bigr)\) abzuleiten hast. Eine verkettete Funktion leitet man folgendermaßen ab.
\(f'(x)=g'\bigl(h(x)\bigr)\cdot h'(x)\)
Regel:
Kettenregel
Ableitung von \(f(x)=g\bigl(h(x)\bigr)\)
\(f'(x)=g'\bigl(h(x)\bigr)\cdot h'(x)\)
Beispiele Kettenregel:
- \(\frac{d}{dx}\)\((2x^2-4)^5=5\cdot(2x^2-4)^4\cdot 4x\)
- \(\frac{d}{dx}\)\(sin(2x)=cos(2x)\cdot 2\)
- \(\frac{d}{dx}\)\(e^{x^2}=e^{x^2}\cdot 2x\)
Die Kettenregel wird unter Anderem auch als "Äußere mal Innere Ableitung" bezeichnet. Dabei ist gemeint, dass man eine verkettete Funktion so ableitet, dass man die äußere Funktion ableitet und diese dann mit der Ableitung der innerne Funktion multipliziert.
Solche verketteten Funktionen lassen sich mit dem Ableitungsrechner von Simplexy ableiten. So kannst du dein Rechenweg überprüfen...
Quotientenregel
Die letzte Ableitungsregel nennt man Quotientenregel, sie hilft bei der Ableitung von Funktionen der Form
\(f(x)=\)\(\frac{g(x)}{h(x)}\)
Eine Funktion die durch ein Quotient zweier Funktionen gebildet wird, leitet sich folgendermaßen ab:
\(f'(x)=\)\(\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{h(x)^2}\)
Regel:
Quotientenregel
Ableitung von \(f(x)=\)\(\frac{g(x)}{h(x)}\)
\(f'(x)=\)\(\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{h(x)^2}\)
Beispiele Quotientenregel:
- \(\frac{d}{dx}\)\(\frac{x}{2x+1}=\frac{1\cdot(2x+1)-x\cdot 2}{(2x+1)^2}\)
- \(\frac{d}{dx}\)\(\frac{x^2+x}{2x+x^3}=\frac{(2x+1)\cdot (2x+x^3)-(x^2+x)\cdot(2+3x^2)}{(2x+x^3)^2}\)
- \(\frac{d}{dx}\)\(\frac{e^x}{sin(x)}=\frac{e^x\cdot sin(x)-e^x\cdot cos(x)}{sin(x)^2}\)
Ableitung wichtiger Funktionen
In dem rest von diesem Beitrag werden wichtige Funktionen und der Ableitung angegeben. Zu einigen der Funktionen werden Beispiele berechnet. Diese Funktionen lassen sich auch mit dem Ableitungsrechner ableiten.
Wurzelfunktion ableiten
\(\begin{aligned} f(x)&=\sqrt{x}\\ \\ f'(x)&=\frac{1}{2\sqrt{x}} \end{aligned}\)
Hier muss man darauf achten, ob in der Wurzefunktion nur ein \(x\) steht oder zusätzlich noch etwas anderes. Sollte unter der Wurzel mehr als nur ein \(x\) stehen (z.B \(2x\)), so muss man die Kettenregel anwenden.
Beispiel Wurzelfunktion ableiten
Berechne die Ableitung der folgenden Wurzelfunktion
\(f(x)=\sqrt{2x}\)
Lösung:
Da unter der Wurzel nicht nur ein \(x\) steht, haben wir es mit einer verketteten Funktion zu tun.
\(f(x)=g(h(x))\)
daher müssen wir die Kettenregel bei der Ableitung nutzen.
Hier ist die äußere Funktion:
\(g(x)=\sqrt{x}\)
Die innere Funktion lautet:
\(h(x)=2x\)
Wie wir bereits wissen berechnet sich die Ableitung einer verketteten Funktion wie folgt:
\(f'(x)=g'(h(x))\cdot h'(x)\)
Dass kann man nun anwenden:
\(\begin{aligned} f'(x)&=\underbrace{\frac{1}{2\sqrt{2x}}}_{g'(h(x))}\cdot \underbrace{2}_{h'(x)} \\ \\ &=\frac{1}{\sqrt{2x}} \end{aligned}\)
Als Lösung erhalten wir damit:
\(\begin{aligned} f'(x)&=\frac{1}{\sqrt{2x}} \end{aligned}\)
Die Ableitung einer Wurzelfunktion kann man mit dem Ableitungsrechner berechnen. So kannst du dein Ergebnis jederzeit überprüfen.
e-Funktion ableiten
\(\begin{aligned} f(x)&=e^x\\ \\ f'(x)&=e^x \end{aligned}\)
Das ableiten einer \(e\)-Funktion ist sehr einfach, denn die Ableitung der \(e\)-Funktion ergibt wieder die \(e\)-Funktion. Das kann man mit dem Ableitungsrechner schnell überprüfen. Ähnlich wie bei der Ableitung der Wurzelfunktion muss man darauf achten ob im Exponenten der \(e\)-Funktion mehr als nur \(x\) steht. Wenn dort mehr als \(x\) steht, so muss man die Kettenregel beim ableiten anwenden.
Beispiel
Als Beispiel für das anwenden der Kettenregel beim ableiten der \(e\)-Funktion berechnen wir das folgende Beispiel:
\(f(x)=e^{2x}\)
Lösung:
Da im Exponenten der \(e\)-Funktion \(2x\) steht, haben wir es mit einer verketteten Funktion zu tun
\(f(x)=g(h(x))\)
wir müssen alsi die Kettenregel bei der Ableitung anwenden.
Die äußere Funktion lautet:
\(g(x)=e^x\)
und die innere Funktion ist:
\(h(x)=2x\)
Wie wir bereits wissen wird eine verkettete Funktion wie folgt abgeleitet:
\(f'(x)=g'(h(x))\cdot h'(x)\)
Das werden wir nun anwenden:
\(f'(x)=\underbrace{e^{2x}}_{g'(h(x))}\cdot \underbrace{2}_{h'(x)}\)
Als Lösung erhalten wir damit:
\(f'(x)=2\cdot e^{2x}\)
Der Ableitungsrechner von Simplexy kann solche verketteten \(e\)-Funktionen ableiten.
Logarithmus Funktion ableiten
\(\begin{aligned} f(x)&=ln(x)\\ \\ f'(x)&=\frac{1}{x} \end{aligned}\)
Die Ableitung vom natürlichen Logarithmus lautet eins durch \(x\). Man muss auch hier darauf achten ob in der \(ln\) funktion mehr als nur ein \(x\) steht. Sollte dort mehr als \(x\) stehen, so muss man wieder die Kettenregel beim ableiten anwenden.
Beispiel
Berechne die Ableitung der folgenden Logarithmus Funktion
\(f(x)=ln(2x)\)
Lösung:
Da im \(ln\) nicht nur ein \(x\) sondern \(2x\) steht, haben wir es mit einer verketteten Funktion zu tun.
\(f(x)=g(h(x))\)
daher müssen wir die Kettenregel bei der Ableitung betrachten.
Die äußere Funktion lautet:
\(g(x)=ln(x)\)
Die innere Funktion lautet:
\(h(x)=2x\)
Wir wissen, dass sich die Ableitung einer verketteten Funktion wie folgt berechnet:
\(f'(x)=g'(h(x))\cdot h'(x)\)
Dass kann man nun anwenden und man erhält:
\(f'(x)=\underbrace{\frac{1}{2x}}_{g'(h(x))}\cdot \underbrace{2}_{h'(x)}\)
Als Lösung erhalten wir damit:
\(f'(x)=\)\(\frac{1}{x}\)
Sinusfunktion ableiten
\(\begin{aligned} f(x)&=sin(x)\\ \\ f'(x)&=cos(x) \end{aligned}\)
Die Ableitung von der Sinusfunktion ist die Cosinusfunktion. Das kann man sich sehr leicht merken. Jedoch muss man wieder darauf achten ob im sinus mehr als nur ein \(x\) steht. Dann muss man nämlich die Kettenregel bei der Ableitung anwenden.
Beispiel
Leite die folgende Funktion ab
\(f(x)=sin(2x)\)
Lösung:
Es scheint als hätten wir es wieder mit einer verketteten Funktion zu tun. Im sinus steht nicht nur ein \(x\):
\(f(x)=g(h(x))\)
Wir müssen also die Kettenregel bei der Ableitung betrachten.
Die äußere Funktion ist:
\(g(x)=sin(x)\)
Die innere Funktion lautet:
\(h(x)=2x\)
Wir haben bereits oft die Kettenregel angewendet, sie lautet:
\(f'(x)=g'(h(x))\cdot h'(x)\)
Man erhält also:
\(f'(x)=\underbrace{cos(2x)}_{g'(h(x))}\cdot \underbrace{2}_{h'(x)}\)
Als Lösung erhalten wir damit:
\(f'(x)=2\cdot cos(2x)\)
Mit dem Ableitungsrechner von Simplexy kann man auch Winkelfunktionen wie der Sinus und der Cosinus ableiten.
Cosinusfunktion ableiten
\(\begin{aligned} f(x)&=cos(x)\\ \\ f'(x)&=-sin(x) \end{aligned}\)
Die Ableitung von der Cosinusfunktion ist die Minus Sinusfunktion. Das kann man sich ebenfalls leicht merken. Auch hier muss man wieder darauf achten das im Cosinus nicht mehr als ein \(x\) steht. Ansonsten muss man bei der Ableitung wieder die Kettenregel nutzen.
Beispiel
Berechne die Ableitung der folgenden Cosinus Funktion
\(f(x)=cos(2x)\)
Lösung:
Weil im Cosinus mehr als nur ein \(x\) steht, haben wir es mit einer verketteten Funktion zu tun
\(f(x)=g(h(x))\)
daher müssen wir die Kettenregel bei der Ableitung nutzen.
Die äußere Funktion lautet:
\(g(x)=cos(x)\)
und die innere Funktion ist:
\(h(x)=2x\)
Wir können wieder die Kettenregel nutzen, sie lautet:
\(f'(x)=g'(h(x))\cdot h'(x)\)
Wendet man das an, so erhält man:
\(f'(x)=\underbrace{-sin(2x)}_{g'(h(x))}\cdot \underbrace{2}_{h'(x)}\)
Als Lösung erhalten wir damit:
\(f'(x)=-2\cdot sin(2x)\)
Mit dem Ableitungsrechner kann man solche verketteten Funktionen leicht ableiten.
