Symmetrieverhalten
Online Rechner
Der Online Rechner von Simplexy kann dir beim Symmetrieverhalten einer Funktion sehr helfen. Mit dem Rechner kannst du dir den Graphen einer Funktion zeichnen lassen, die Funktion ableiten und viel mehr.
Symmetrie einer Funktion
Beim Symmetrieverhalten einer Funktion geht es darum, ob der Graph zur \(y\)-Achse oder zu einem Punkt (z.B. Ursprung) symmetrisch ist. Im folgenden Video findest du eine Einleitung zum Thema Symmetrie von Funktionen:
Im Video wurden zwei Arten von Symmetrien eingeführt. Zum einen die Achsensymmetrie und zum anderen die Punktsymmetrie. Mit diesen zwei Symmetrien werden wir uns im folgenden beschäftigen.
Achsensymmetrie
Eine Achsensymmetrie zur y-Achse liegt beispielsweise bei der Normalparabel vor.
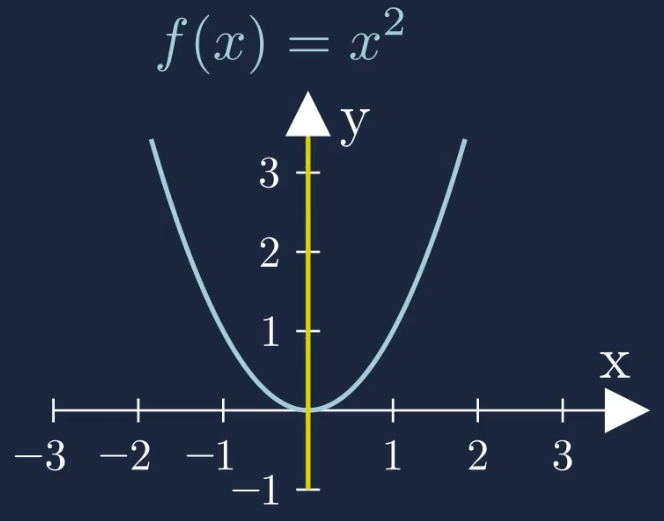
Achsensymmetrie zur y-Achse
\(f(-x)=f(x)\)
Möchte man zeigen, das eine Funktion eine Achsensymmetrie zur y-Achse besitzt, so muss man \(-x\) in die Funktion einsetzen und überprüfen ob das Ergbnis gleich \(f(x)\) ist.
Beispiel zur Achsensymmetrie
Zeige das die folgende Funktion Achsensymmetrisch zur y-Achse ist.
\(f(x)=x^4-x^2\)
Um die Achsensymmetrie zur zeigen, müssen wir folgendes zeigen:
\(f(-x)=f(x)\)
Dazu setzen wir \(\textcolor{blue}{-x}\) in die Funktion ein
\(f(\textcolor{blue}{-x})=(\textcolor{blue}{-x})^4-(\textcolor{blue}{-x})^2=x^4-x^2=f(x)\)
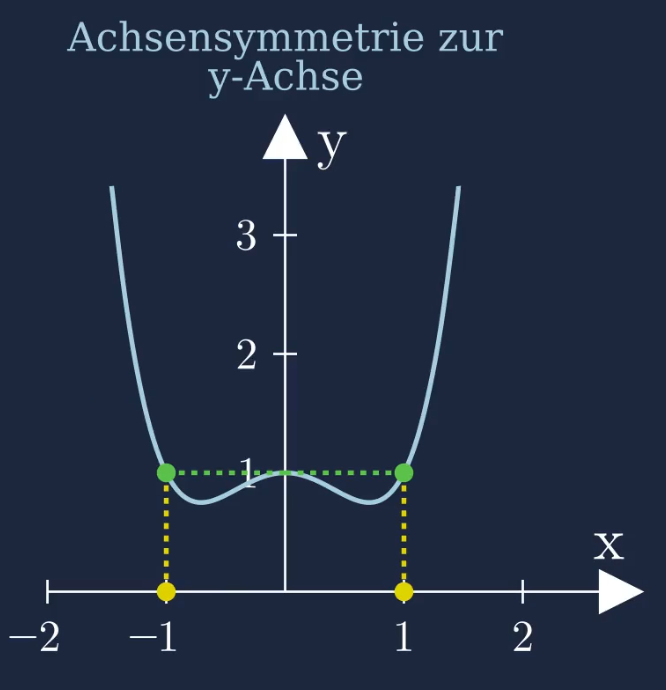
Achsensymmetrie zur beliebigen Achse
Eine achsensymmetrische Funktion kann entlang der \(x\)-Achse verschoben werden. Damit verschiebt sich auch die Achsensymmetrie. Eine Achsensymmetrie kann zu einer beliebigen Achse vorliegen.
Achsensymmetrie zu einer beliebigen Achse
\(f(x_0+h)=f(x_0-h)\)
Dabei ist \(x_0\) die Verschiebung entlange der x-Achse und \(h\) eine beliebige konstante.
Beispiel
Ziege das die folgende Funktion eine Achsensymmetrie zur Achse \(x_0=2\) besitzt:
\(f(x)=(x-2)^2\)
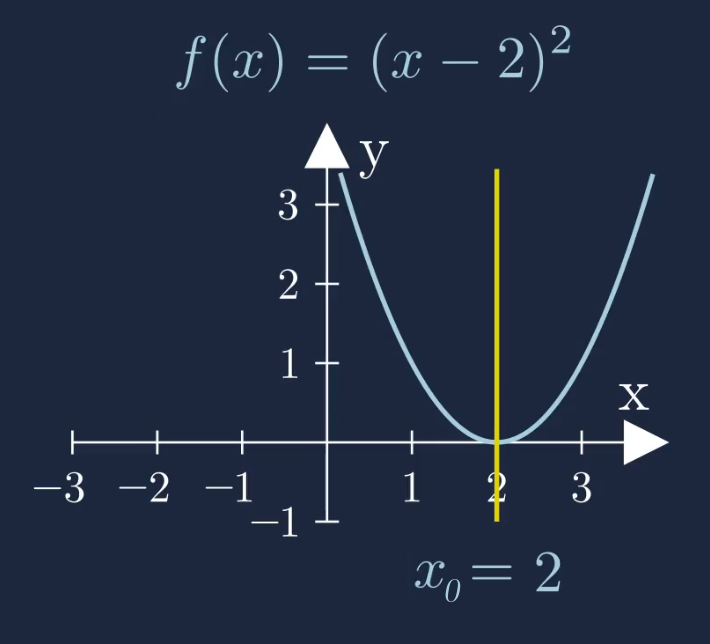
Um zu zeigen dass die Funktion eine Achsensymmetrie zur Achse \(x_0=2\) besitzt, müssen wir zeigen, dass
\(f(x_0+h)=f(x_0-h)\)
Als erstes setzen wir \(x_0+h\) in die Funktion ein:
\(\begin{aligned} f(\textcolor{blue}{x_0+h})=(\textcolor{blue}{2+h}-2)^2=h^2 \end{aligned}\)
Nun setzen wir \(\textcolor{red}{x_0-h}\) in die Funktion ein:
\(\begin{aligned} f(\textcolor{red}{x_0-h})=(\textcolor{red}{2-h}-2)^2=(-h)^2=h^2 \end{aligned}\)
Wir haben in beiden Fällen als Ergebnis \(h^2\) erhalten. Damit gilt also:
\(f(\textcolor{blue}{x_0+h})=f(\textcolor{red}{x_0-h})\)
Die Funktion ist damit symmetrisch zur Achse \(x_0=2\)
Punktsymmetrie zum Ursprung
Eine weitere wichtige Symmetrie mit der wir uns beschäftigen ist die Punktsymmetrie zum Ursprung.
Punktsymmetrie zum Ursprung liegt vor, wenn gilt:
\(f(-x)=-f(x)\)
Beispiel Punktsymmetrie zum Ursprung
Zeige das die folgende Funktion punktsymmetrisch zum Ursprung ist:
\(f(x)=x^3\)
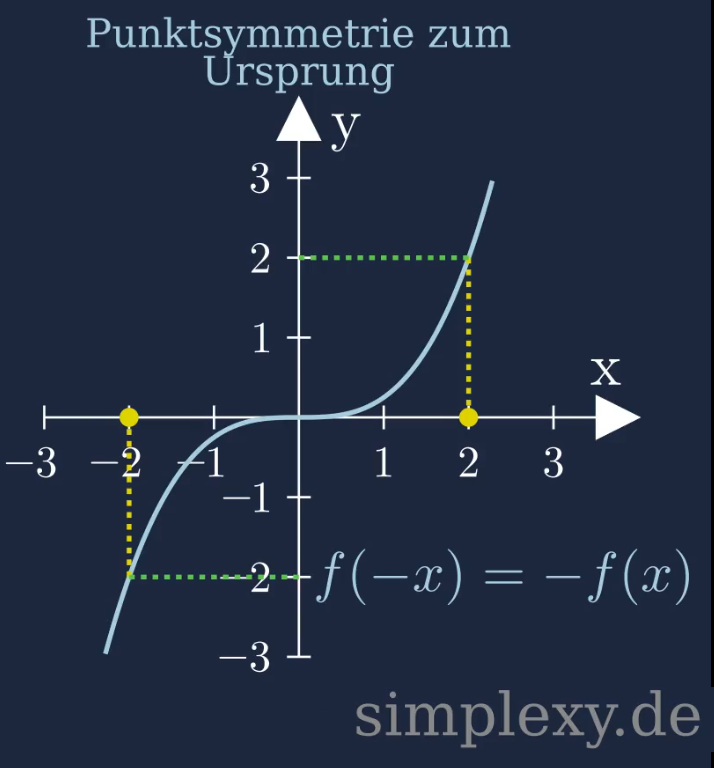
Um zu zeigen, dass die Funktion Punktsymmetrisch zum Ursprung ist, müssen wir \(\textcolor{red}{-x}\) in die funktion einsetzen:
\(\begin{aligned} f(\textcolor{red}{-x})&=(\textcolor{red}{-x})^3\\ &=(-x)\cdot(-x)\cdot(-x)\\ &=-x^3=-f(x) \end{aligned}\)
Damit gilt:
\(f(-x)=-f(x)\)
und die Funktion ist Achsensymmetrisch zum Ursprung.
Achsensymmetrie zu einem beliebigen Punkt
Die Symmetrie zu einem beliebigen Punkt liegt vor, wenn gilt:
\(f(x_0+h)-y_0=-f(x_0-h)+y_0\)
Dabei sind \(x_0\) und \(y_0\) die Koordinaten des Symmetrie-Punktes.
Um zu zeigen, dass eine Funktion symmetrisch zu einem Punkt mit den Koordinaten \((x_0|y_0)\) ist, muss man \(f(x_0+h)-y_0\) berechnen und -\(f(x_0-h)+y_0\) berechnen und zeigen das beide gleich sind.
Beispiel Punktsymmetrie zu einem beliebigen Punkt.
Zeige das die folgende Funktion eine Punktsymmetrie bzgl. des Punktes \(P(2|1)\) besitzt:
\(f(x)=(x-2)^3+1\)
Um die Punktsymmetrie zu zeigen müssen wir als erstes \(f(\textcolor{blue}{x_0+h})-\textcolor{red}{y_0}\) berechnen:
\(\begin{aligned} f(\textcolor{blue}{x_0+h})-\textcolor{red}{y_0}&=(\textcolor{blue}{2+h}-2)^3+1-\textcolor{red}{1}\\ &=h^3 \end{aligned}\)
Als nächstes müssen wir \(-f(\textcolor{blue}{x_0-h})+\textcolor{red}{y_0}\) berechnen:
\(\begin{aligned} -f(\textcolor{blue}{x_0-h})+\textcolor{red}{y_0}&=-(\textcolor{blue}{2-h}-2)^3-1+\textcolor{red}{1}\\ &=-(-h)^3=h^3 \end{aligned}\)
Wir erhalten in beiden Fällen als Ergebnis \(h^3\), damit ist die Funktion Punktsymmetrisch zum Punkt \(P(2|1)\).
