Fläche unter einem Graphen berechnen
Integralrechner
Der Integral Rechner von Simplexy kann dir die Fläche unter einem Graphen berechnen. Nutze den Integralrechner um das bestimmte und unbestimmte Integal von Funktionen zu ermitteln.
Fläche unter einem Graphen bestimmten
Um die Fläche unter einem Graphen berechnen zu können, muss man das bestimmte Integral verwenden. Die Fläche unter einem Graphen wird stets in einem betimmten Intervall berechnet. Das Intervall bildet die Integrationsgrenzen des bestimmten Integrals.
Wie man die Fläche unter einer Funktion berechnen kann, wird dir direkt an einem Beispiel gezeigt. Berechne die Fläche unter der Funktion \(f(x)=x\) im Intervall \([1,3]\).

Die Fläche A lässt sich mit dem bestimmten Integral berechnen:
\(A=\displaystyle\int_{\color{green}{1}}^{\color{blue}{3}} x\,\,dx\)
Schritt 1
Berechne die Stammfunktion \(F(x)\)
\(F(x)=\frac{1}{2}x^2\)
Schritt 2
Deute an, dass du die Integrationsgrenzen in die Stammfunktion einsetzen wirst. Dies machst du mit Hilfe von eckigen Klammern.
\(\displaystyle\int_{\color{green}{1}}^{\color{blue}{3}} x\,\,dx=\Bigg[F(x)\Bigg]_{\color{green}{1}}^{\color{blue}{3}}=\Bigg[\frac{1}{2}x^2\Bigg]_{\color{green}{1}}^{\color{blue}{3}}\)
Schritt 3
Nun kannst du das bestimmte Integral berechnen indem du das folgende ausrechnest:
\(F({\color{blue}{3}})-F({\color{green}{1}})\)
also \(F({\color{blue}{\text{obere Grenze}}})\) minus \(F({\color{green}{\text{untere Grenze}}})\)
\(\begin{aligned} \displaystyle\int_{\color{green}{1}}^{\color{blue}{3}} x\,\,dx&=\Bigg[\frac{1}{2}x^2\Bigg]_{\color{green}{1}}^{\color{blue}{3}}\\ \\ &=\big(\frac{1}{2}{\color{blue}{3}}^2\big)-\big(\frac{1}{2}{\color{green}{1}}^2\big)\\ \\ &=\frac{9}{2}-\frac{1}{2}=4 \end{aligned}\)
Die Fläche unter der Funktion \(f(x)=x\) im Intervall \([1,3]\) ist \(4\) Flächeneinheiten groß.
\(A=4\,\,FE\)
Negativer und positiver Flächeninhalt
Sind die Integrationsgrenzen so gewählt, dass ein Teil der Funktion unterhalb der x-Achse und ein Teil oberhalb der x-Achse liegt, so muss man das Integral aufteilen.
Betrachten wir als Beispiel die Funktion
\(f(x)=x\)
Nun möchten wir die Fläche unter der Funktion im Intervall \([-3,3]\) berechnen.

Würde man die Fläche unter der Funktion mit dem folgenden bestimmten Integral berechnen:
\(A=\displaystyle\int_{\color{green}{-3}}^{\color{blue}{3}} x\,\,dx\)
So würde man einen Flächeninhalt von Null erhalten.
\(\begin{aligned} A&=\displaystyle\int_{\color{green}{-3}}^{\color{blue}{3}} x\,\,dx=\Bigg[\frac{1}{2}x^2\Bigg]_{\color{green}{-3}}^{\color{blue}{3}}\\ \\ &=\big(\frac{1}{2}{\color{blue}{3}}^2\big)-\big(\frac{1}{2}({\color{green}{-3}}^2)\big)\\ \\ &=\frac{9}{2}-\frac{9}{2}=0 \end{aligned}\)
Die Fläche zwischen der Funktion und der x-Achse ist jedoch nicht gleich Null. Um den Flächeninhalt richtig zu berechnen muss man das bestimmte Integral aufteilen. Dabei muss die Fläche die unterhalb der x-Achse liegt und die Fläche welche oberhalb der x-Achse liegt separat berechnen und davon dann den Betrag bilden.
\(\begin{aligned} A&=\displaystyle\int_{\color{green}{-3}}^{\color{blue}{3}} x\,\,dx\\ \\ &=\Bigg|\displaystyle\int_{\color{green}{-3}}^{\color{black}{0}} x\,\,dx\Bigg|+\Bigg|\displaystyle\int_{\color{black}{0}}^{\color{blue}{3}} x\,\,dx\Bigg|\\ \\ &=\Bigg|\Big[\frac{1}{2}x^2\Big]_{\color{green}{-3}}^{\color{black}{0}}\Bigg|+\Bigg|\Big[\frac{1}{2}x^2\Big]_{\color{black}{0}}^{\color{blue}{3}}\Bigg|\\ \\ &=\Bigg|-\frac{9}{2}\Bigg|+\Bigg|\frac{9}{2}\Bigg|\\ \\ &=\frac{9}{2}+\frac{9}{2}=9 \end{aligned}\)
Die Fläche unter der Funktion ist \(9\) Flächeneinheiten groß.
Weiteres Beispiel
Nun betrachten wir die Funktion \(sin(x)\) und fragen uns wie groß die Fläche zwischen der Kurve und der x-Achse im Intervall \([-\pi,\pi]\) ist.
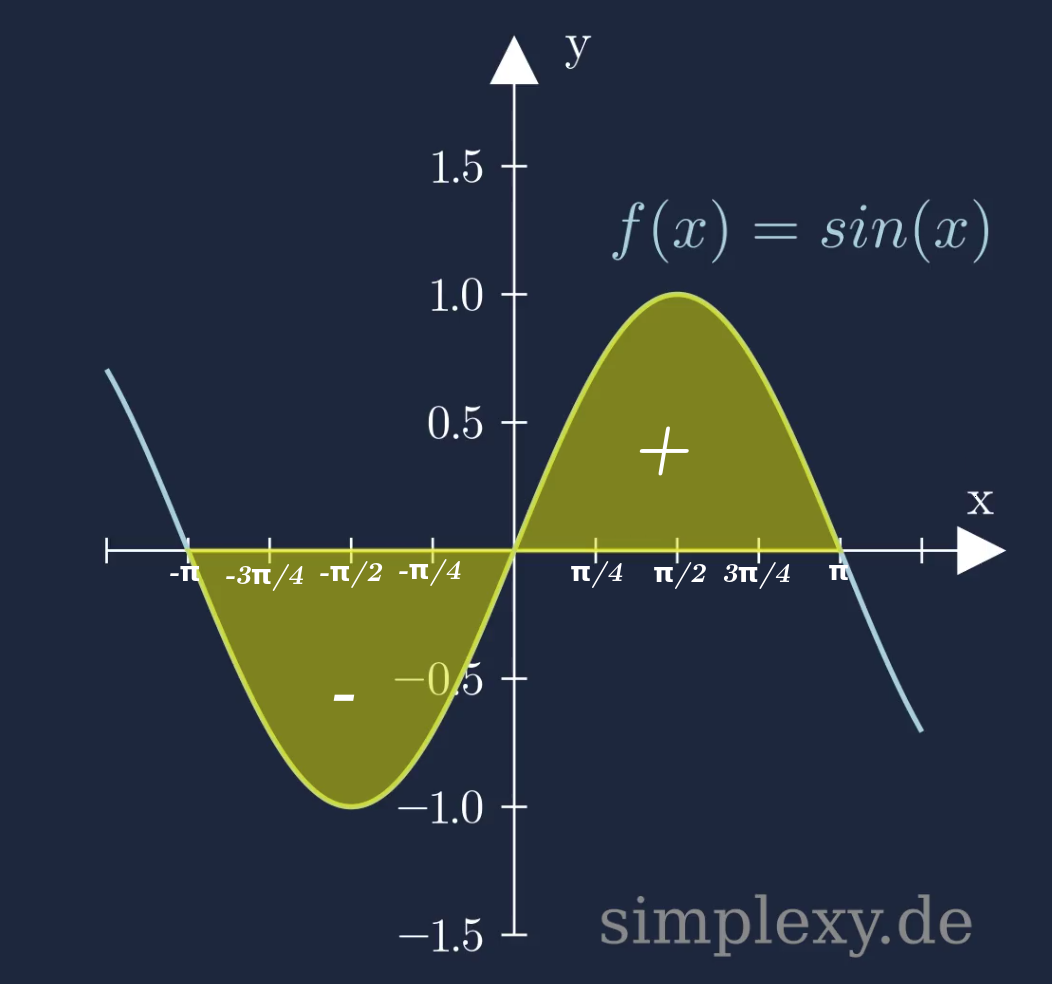
Die Fläche erhält man über das bestimmte Integral
\(\displaystyle\int_{-\pi}^{\pi} sin(x)\,\,dx\)
Um dieses bestimmte Integral zu berechnen führen wir die folgenden Schritte aus:
Schritt 1
Berechne die Stammfunktion \(F(x)\)
\(F(x)=-cos(x)\)
Schritt 2
Deute an, dass du die Integrationsgrenzen in die Stammfunktion einsetzen wirst. Dies machst du mit Hilfe von eckigen Klammern.
\(\begin{aligned} \displaystyle\int_{\color{green}{-\pi}}^{\color{blue}{\pi}} sin(x)\,\,dx&=\bigg[F(x)\bigg]_{\color{green}{-\pi}}^{\color{blue}{\pi}}\\ \\ &=\big[-cos(x)\big]_{\color{green}{-\pi}}^{\color{blue}{\pi}} \end{aligned}\)
Schritt 3
Nun kannst du das bestimmte Integral berechnen indem du das folgende ausrechnest:
\(F({\color{blue}{\pi}})-F({\color{green}{-\pi}})\)
also \(F({\color{blue}{\text{obere Grenze}}})\) minus \(F({\color{green}{\text{untere Grenze}}})\)
\(\begin{aligned} \displaystyle\int_{\color{green}{-\pi}}^{\color{blue}{\pi}} sin(x)\,\,dx&=\Bigg[-cos(x)\Bigg]_{\color{green}{-\pi}}^{\color{blue}{\pi}}\\ \\ &=-cos({\color{blue}{\pi}})-\big(-cos({\color{green}{-\pi}})\big)\\ \\ &=1-1=0 \end{aligned}\)
Nun stellt sich die Frage warum das bestimmte Integral gleich null ist, obwohl die Fläche ungleich Null ist.
Auch hier ist es darauf zurück zuführen, dass das bestimmte Integral negative und positive Werte liefern kann.
Besonderheit bei der Flächenberechnung
Das bestimmte Integral liefert positive und negative Flächeninhalte.
An dem Beispiel mit der Sinus-Funktion sieht man, der Flächeninhalt zwischen dem Graph und der x-Achse lässt sich nicht so leicht berechnen, wenn die Funktion innerhalb der Integrationsgrenzen sowohl unterhalb als auch oberhalb der x-Achse verläuft. In solchen Fällen muss man das bestimmte Integral aufteilen. Dabei wird das bestimmte Integral so aufgeteilt, dass man von einer Nullstelle der Funktion zur nächsten Nullstelle integriert und die Beträge davon werden addiert. Am beispiel der Sinus-Funktion geht man also wie folgt vor um die Fläche A zwischen dem Graphen und der x-Achse zu berechnen.
\(\begin{aligned} A&=\Bigg|\displaystyle\int_{-\pi}^{0} sin(x)\,\,dx\Bigg|+\Bigg|\displaystyle\int_{0}^{\pi} sin(x)\,\,dx\Bigg|\\ \\ &=\Bigg|\Big[-cos(x)\Big]_{-\pi}^{0}\Bigg|+\Bigg|\Big[-cos(x)\Big]_{0}^{\pi}\Bigg|\\ \\ &=\Big|-cos(0)+cos(-\pi)\Big|+\Big|-cos(\pi)+cos(0)\Big|\\ \\ &=2+2=4 \end{aligned}\)
Damit ist die Fläche zwischen dem Graphen der Funktion \(f(x)=sin(x)\) und der x-Achse im Intervall \([-\pi,\pi]\) genau \(4\) Flächeneinheiten groß.
Fläche unter einer Funktion mit Vorzeichenwechsel berechnen
Wie in den letzten zwei Beispielen gezeigt, können Funktionen einen Vorzeichenwechsel durchführen. Das heißt, ein Teil der Funktion liegt oberhalb der x-Achse und ein Teil liegt unterhalb der x-Achse. Muss man die Fläche zwischen einer Funktion und der x-Achse in einem Intervall berechnen, bei dem die Funktion einen Vorzeichenwechsel durchführt, so muss man diese Schritte anwenden.
Schritt 1
Bestimme die Nullstelle bzw. Nullstellen der Funktion.
Schritt 2
Integrier vom Anfang des Intervall bis zur Nullstelle.
Schritt 3
Integrier von der Nullstelle bis zum Endpunkt des Intervall.
Sind mehrere Nullstellen vorhanden, dann integrierst du von Nullstelle zur Nullstelle.
Schritt 4
Addiere die Ergebnisse, achte dabei unbedingt darauf, dass du die Beträge addierst (also ohne Minus). Dann hast du die Fläche zwischen einer Funktion und der x-Achse berechnen können.
