Stammfunktion 1/x
Stammfunktion Rechner
Der Stammfunktion Rechner von Simplexy kann dir die Stammfunktion von Brüchen berechnen und noch viel mehr. Nutze den Integralrechner um das bestimmte und unbestimmte Integal von Funktionen zu ermitteln.
Stammfunktion 1/x
1/x Stammfunktion
\(\displaystyle\int \frac{1}{x}=ln(|x|)+c\)
Wie du womöglich schon weist lässt sich ein Bruch in eine Potzenfunktion umschrieben. Die Stammfunktion lässt sich dann leichter berechnen, dass hatten wir in dem Beitrag über die Stammfunktion von Brüchen behandelt.
Bei der Stammfunktion von 1/x kann die Potenzregel nicht angewendet werden. Dies liegt daran, dass die Umschreibung von 1/x in eine Potzenfunktion folgendes ergibt:
\(\frac{1}{x}=x^{-1}\)
Möchte man nun die Potenzregel anwenden, um die Stammfunktion von 1/x berechnen zu können, so wird man festellen, dass im Exponenten eine Null stehen wird. Die Stammfunktion von 1/x lässt sich also auf diesem weg nicht berechnen.
Um 1/x integrieren zu können muss die logarithmische Integrationsregel verwendet werden. Doch zunächst einmal findest du hier das Integral von 1/x:
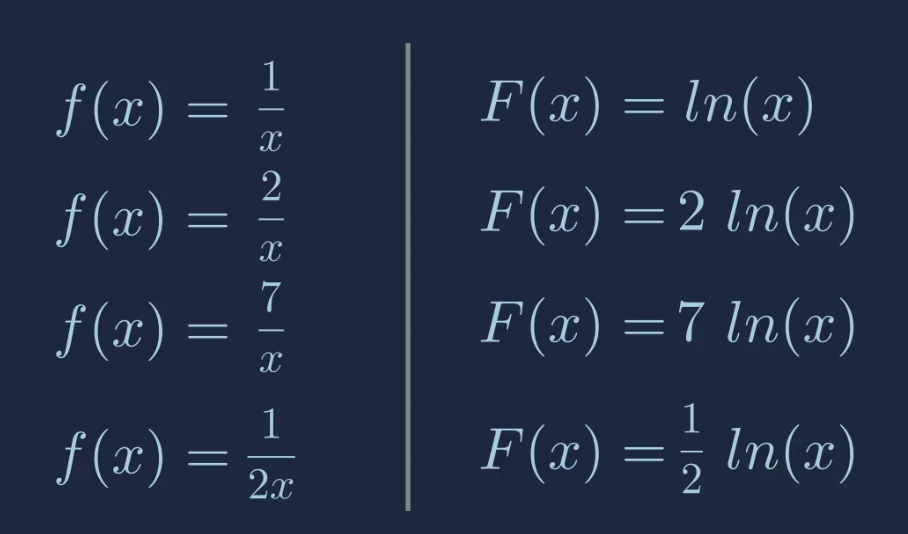
1/x Stammfunktion
\(\displaystyle\int \frac{1}{x}=ln(|x|)+c\)
Dies ist eine Folge der logarithmischen Integrationsregel, welche folgendes besagt:
logarithmische Integrationsregel
\(\displaystyle\int \frac{f'(x)}{f(x)}\,\,dx=ln(|f(x)|)+c\)
Ist \(f(x)=x\) so ist \(f'(x)=1\) und das Integral lautet:
\(\displaystyle\int \frac{f'(x)}{f(x)}\,\,dx=\displaystyle\int \frac{1}{x}\,\,dx=ln(|x|)+c\)
