Matrix invertieren
Inverse Matrix Rechner
Der Matrizenrechner von Simplexy kann beliebige Matrix Rechenoperationen für dich durchführen. Mit dem Inverse Matrix Rechner kannst du ganz einfach eine Matrix invertieren und viel mehr.
Inverse Matrix berechnen
In diesem Beitrag wirst du sehen wie man eine Inverse Matrix berechnen kann. Du wirst sehen wie du Schritt für Schritt eine Matrix invertieren kannst.
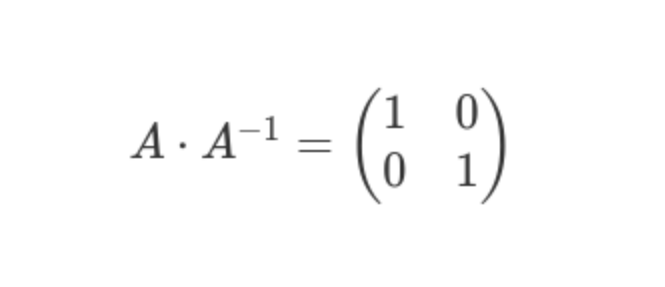
Matrix invertieren erklärt
Die Funktion der Inverse Matrix \(A^{-1}\) ist ähnlich dem sogenannten Kehrwert einer Zahl. Wenn man eine Zahl mit ihrem Kehrwert multipliziert, dann lautet das Ergebnis 1. Ebenso ist es wenn man eine Matrix mit ihrer Inversen multipliziert, als Ergebnis bekommt man die Einheitsmatrix \(E\).
Wiederholung Kehrwert:
\(\begin{aligned} 3\cdot 3^{-1}=3\cdot \frac{1}{3}=1 \end{aligned}\)
\(\begin{aligned} x\cdot x^{-1}=x\cdot \frac{1}{x}=1 \end{aligned}\)
Matrix mit Inverser Matrix multiplizieren
Wenn man eine Matrix \(A\) mit ihrer Inversen Matrix \(A^{-1}\) multipliziert, dann erhält man als Ergebnis die Einheitsmatrix \(E\)
\(A\cdot A^{-1}=E\)
Beispiel Inverse Matrix
\(A=\begin{pmatrix}1 & 2 \\3 &4 \\\end{pmatrix}\)
\(A^{-1}=\begin{pmatrix} -2 & 1 \\ \frac{3}{2} &-\frac{1}{2} \\\end{pmatrix}\)
\(A\cdot A^{-1}=\begin{pmatrix} 1 & 0 \\ 0 & 1\\\end{pmatrix}\)
Ist eine Matrix gegeben, so ist das Ermitteln der Inversen Matrix nicht so einfach wie das ermitteln des Kehrwertes einer Zahl. Es existieren einige Verfahren mit denen die Inverse einer Matrix berechnet werden können. Zu dem ist nicht jede Matrix invertierbar. Es gibt also Matrizen zu denen keine Inverse berechnet werden kann.
Invertierbarkeit einer Matrix
Eine Matrix \(A\) ist genau dann invertierbar, wenn gilt:
\(det(A)\neq 0\)
Ist die Determinante einer Matrix A ungleich null, so sind die Zeilen und Spalten dieser Matrix linear unabhängig. Mehr dazu im Beitrag Determinante berechnen.
2x2 Matrix invertieren
Für eine 2x2 Matrix gibt es eine leicht Formel mit der man die Inverse Matrix berechnen kann. Für eine Matrix \(A\) der folgenden Form:
\(A=\begin{pmatrix}a & b \\c &d \\\end{pmatrix}\)
Berechnet sich die Inverse Matrix \(A^{-1}\) über die folgende Formel:
\(\begin{aligned} A^{-1}=\frac{1}{det(A)}\begin{pmatrix}d & -b \\-c &a \\\end{pmatrix} \end{aligned}\)
Rechenregeln für die Inverse Matrix
Inverse Matrix Regeln
Regel 1
Die Inverse von einem Matrizenprodukt ist gleich dem Produkt aus den Inversen:
\((A\cdot B)^{-1}=A^{-1}\cdot B^{-1}\)
Regel 2
Inverse einer transponierten Matrix und die transponierte der inversen Matrix sind gleich:
\((A^T)^{-1}=(A^{-1})^{T}\)
Regel 3
Die Inverse einer Matrix ist auch invertierbar:
\((A^{-1})^{-1}=A\)
Inverse Matrix berechnen
Wenn du die Inverse Matrix \(A^{-1}\) berechnen möchtest, dann musst du die Einheitsmatrix \(E\) rechts neben der Matrix \(A\) hinschreiben. Als nächstes musst du mit Hilfe von Zeilenumformungen die Einheitsmatrix auf der rechten Seite erzeugen. Die Inverse Matrix kannst du dann auf der rechten Seite ablesen.
\(\begin{aligned} \left( \begin{array}{cc|cc}0 & 1 & 1 & 0\\-1 & 0 & 0 & 1 \\\end{array}\right) \longrightarrow \left( \begin{array}{cc|cc}1 & 0 & 0 & -1\\0 & 1 & 1 & 0 \\\end{array}\right) \end{aligned}\)
Für die Zeilenumformungen kann man den Gauß-Jordan-Algorithmus verwenden. Sobald auf der linken Seite die Einheitsmatrix steht, kann man die inverse Matrix auf der rechten Seite ablesen.
Erweiterte Matrix
Unter der erweiterten Matrix versteht man, die Matrix, in der auf der linken Seite die gegebene Matrix und auf der rechten Seite die Einheitsmatrix steht.
Beispiel Matrix invertieren
Nun betrachten wir eine Beispiel, wie man eine Matrix invertieren kann. Gegebn ist die folgende Matrix:
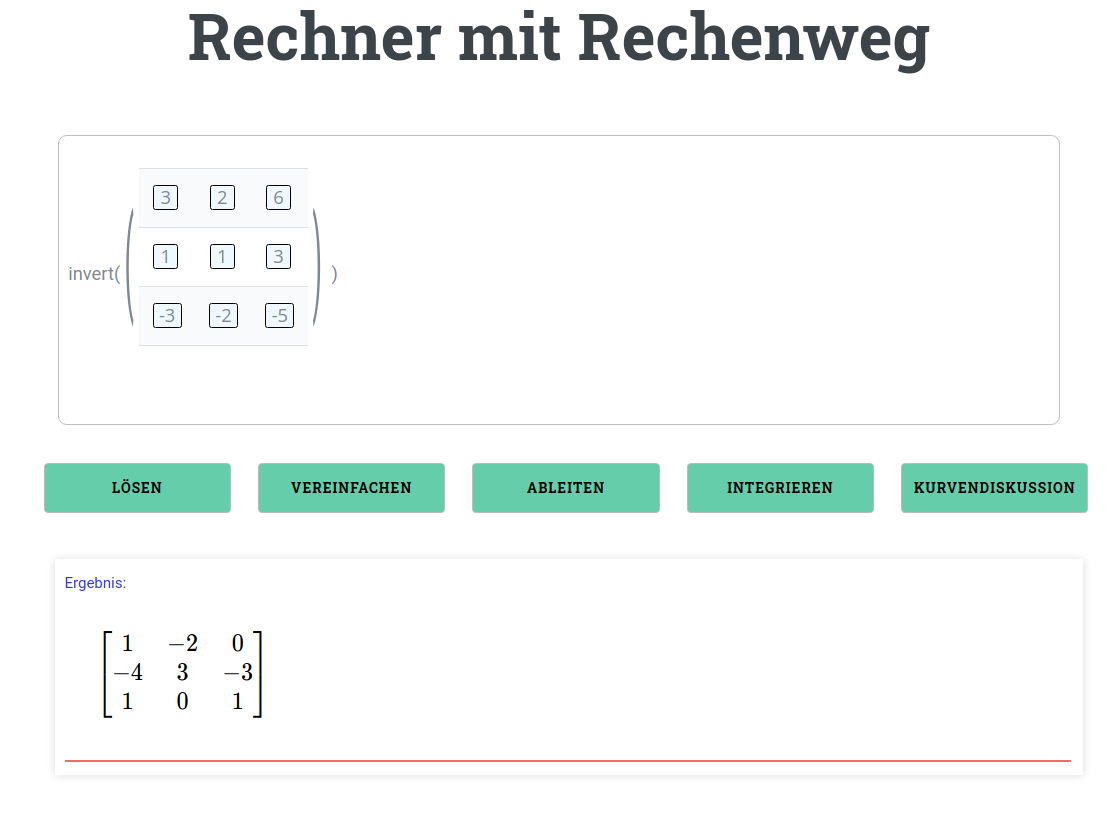
\(\begin{aligned} A=\begin{pmatrix} 3 & 2 & 6 \\ 1 & 1 & 3 \\ -3 & -2 & -5\\\end{pmatrix} \end{aligned}\)
Nun schreiben wir die erweiterte Matrix hin.
\(\begin{aligned} \left( \begin{array}{ccc|ccc}3 & 2 & 6 & 1 & 0 & 0\\1 & 1 & 3 & 0 & 1 & 0 \\ -3 & -2 & -5 & 0 & 0 & 1 \\\end{array}\right) \end{aligned}\)
Durch Zeilenumformungen kann man nun die linke Seite zur Einheitsmatrix verwandeln.
\(\begin{aligned} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 1 & -2 & 0\\0 & 1 & 0 & -4 & 3 & -3 \\ 0 & 0 & 1 & 1 & 0 & 1 \\\end{array}\right) \end{aligned}\)
Auf der rechten Seite steht nun die Inverse Matrix \(A^{-1}\).
\(\begin{aligned} A^{-1}=\begin{pmatrix} 1 & -2 & 0 \\ -4 & 3 & -3 \\ 1 & 0 & 1\\\end{pmatrix} \end{aligned}\)
Du kannst gerne mit dem Matrizenrechner versuchen die Berechnung der Inversenmatrix zu überprüfen.
Matrix nicht invertierbar
Nicht jede Matrix ist invertierbar. Sobald eine Matrix nicht invertierbar ist, wird sie singulär genannt. Hier ein Beispiel für eine nicht invertierbare Matrix.
Nicht invertierbare Matrix Beispiel
\(\begin{aligned} A=\begin{pmatrix} 1 & 2 \\ 2 & 4\\\end{pmatrix} \end{aligned}\)
Die Matrix ist singulär. Die Zeilen der Matrix sind linear abhängig. Für die Determinante der Matrix gilt somit:
\(\begin{aligned} det(A)=0 \end{aligned}\)
Matrix Determinante
Du möchtest mehr über die Determinante einer Matrix lernen. Dann wirf einen Blick auf den Beitrag Determinante berechnen.
