Gerade aus zwei Punkten berechnen
Lineare Funktion Rechner
Der Online Rechner mit Rechenweg von Simplexy kann lineare Funktionen zeichnen, Nullstellen berechnen, y-Achsenabschnitte berechnen und viel mehr.
Lineare Funktion aus zwei Punkten konstruieren
Es ist möglich eine Gerade und die dazu gehörige Geradengleichung aufzustellen, wenn einem lediglich zwei Punkten im Koordinatensystem gegeben sind.
Nehmen wir mal an dir sind der Punkt \(Q=(-2|-4)\) und der Punkt \(P(2|2)\) gegeben, wie erhält man daraus die Geradengleichung ?
Zunächst einmal eine Skizze:
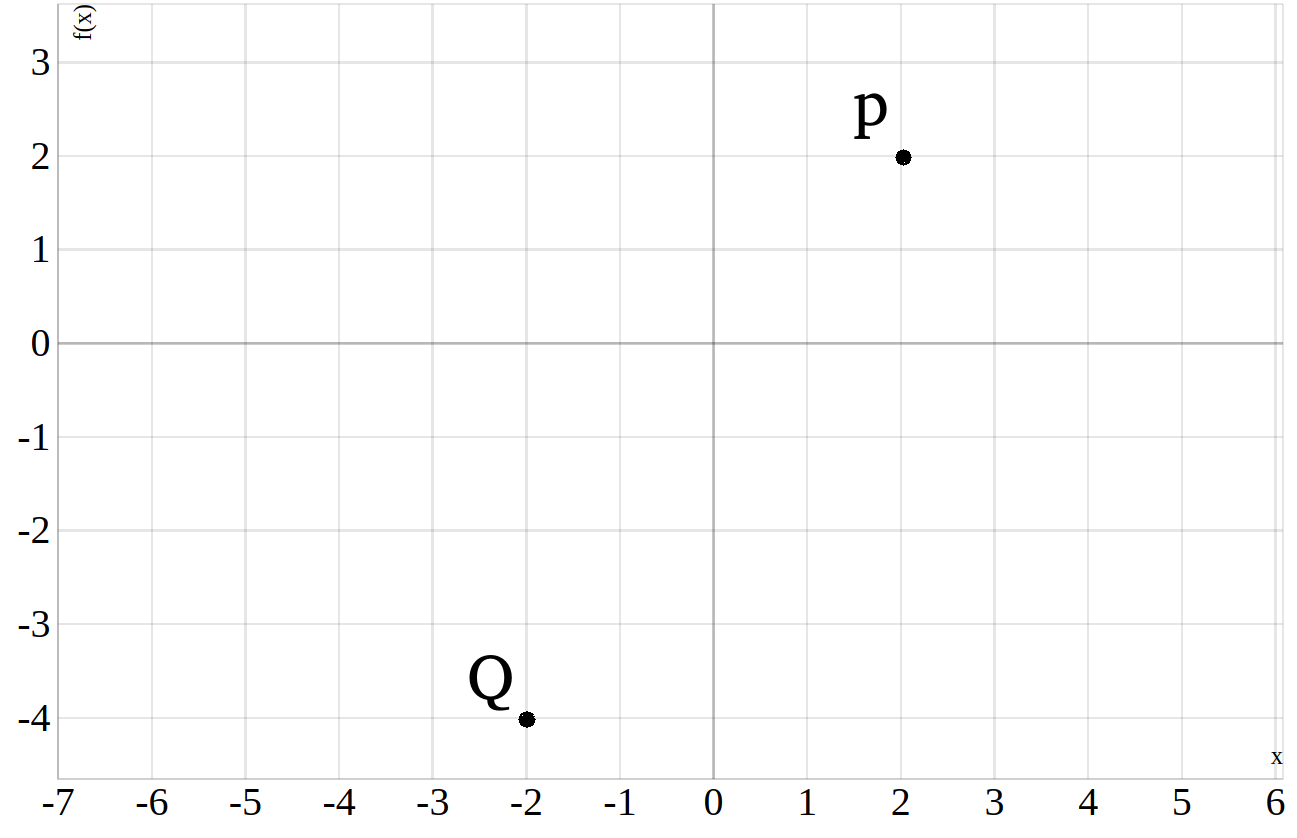
Um auf die Gerade zu kommen die durch beide Punkte \(Q\) und \(P\) geht, brauchen wir die allgemeine Geradengleichung
\(f(x)=m\cdot x+b\). Wir müssen also \(m\) und \(b\) ermitteln.
Steigung berechnen
Die Steigung erhältst du über die Formel \(m=\frac{y_Q-y_P}{x_Q-x_P}\). Wobei \(y_Q\) die \(y\)-Koordinate des Punktes \(Q\) ist und \(y_P\) ist die \(y\)-Koordinate des Punktes \(p\). Das gleiche gilt natürlich im bezug auf \(x_Q\) und \(x_P\). Setzen wir mal unsere Werte in die Gleichung ein.
\(\begin{aligned} m=\frac{-4-2}{-2-2}=\frac{-6}{-4}=\frac{3}{2} \end{aligned}\)
Es ist übrigens Egal ob man \(m=\frac{y_Q-y_P}{x_Q-x_P}\) oder \(m=\frac{y_P-y_Q}{x_P-x_Q}\) rechnet. Es kommt das gleiche Ergbnis bei raus, probier es mal aus.
y Achsenabschnitt berechnen
Den \(y\)-Achsenabschnitt erhälts du, in dem du entweder den Punkt \(Q\) oder den Punkt \(P\) in die allgemeine Geradengleichung einsetzt. Dabei ist es vollkommen egal welchen der zwei Punkte du benutzt.
Wir benutzen mal den Punkt \(Q\) und setzen \(Q=(-2|-4)\) in die allgemeine Geradengleichung \(f(x)=m\cdot x+b\) ein. Das heißt
\(f(x)=-4\), \(\,x=-2\) und die Steigung \(m=\frac{3}{2}\) haben wir Oben berechnet.
Nach dem Einsetzten erhalten wir:
\(\begin{aligned} -4=\frac{3}{2}\cdot (-2)+b \end{aligned}\)
Um auf \(b\) zu kommen müssen wir diese Gleichung jetzt nach \(b\) umformen
\(\begin{aligned} -4&=\frac{3}{2}\cdot (-2)+b\,\,\,\,|-b\\ \\ -4-b&=-3\\ \\ -4-b&=-3\,\,\,\,|+4\\ \\ -b&=-3+4\\ \\ -b&=1\,\,\,\,\,\,\,\,\,\,\,\,|\cdot (-1)\\ \\ b&=-1 \end{aligned}\)
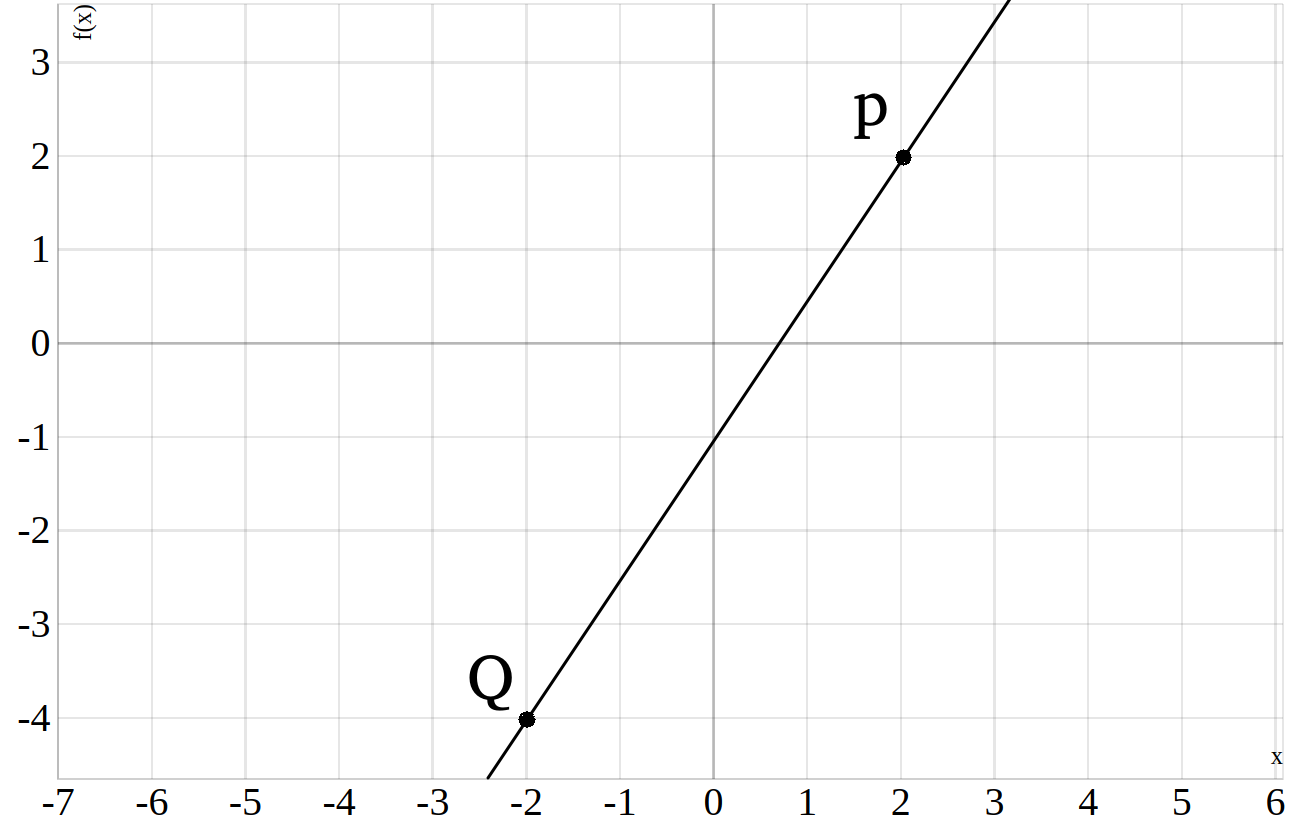
Damit haben wir ausgehend von den zwei gegebenen Punkten, die Steigung \(m\) und den \(y\)-Achsenabschnitt berechnet. Mit Hilfe einer Skizze kannst du deine Ergebnisse immer überprüfen. Die Gerade durch die Punkte \(Q=(-2|4)\) und \(P(2|2)\) lässt sich schreiben als \(f(x)=\frac{3}{2}\cdot x - 1\).
Falls du das Umstellen einer Gleichung noch nicht gut beherrschst, oder das Lösen von Gleichungen üben möchtest, dann kannst du es hier nochmal wiederholen.
Lineare Funktion aus zwei Punkten konstruieren - Vorgehen
Die Steigung einer Geraden die durch die zwei Punkte \(Q(x_Q|y_Q)\)
und \(P(x_P|y_P)\) geht, erhälts du über die Formel:Den \(y\)-Achsenabschnitt berechnet man, indem man einen der gegebenen Punkte in die Geradengleichung \(f(x)=m\cdot x+b\) einsetzt und nach \(b\) umstellst.
\(m=\frac{y_P-y_Q}{x_P-x_Q}\)
