Lineare Funktionen
Lineare Funktion Rechner
Der Online Rechner mit Rechenweg von Simplexy kann lineare Funktionen zeichnen, Nullstellen berechnen, Y-Achsenabschnitte berechnen und viel mehr.
Lineare Funktion einfach erklärt
In diesem Beitrag wirst du verstehen was lineare Funktionen sind und wie man eine lineare Funktion berechnen kann. Des Weiteren wirst du Beispielaufgaben zu Geraden und der Geradengleichung sehen.
Eine Lineare Funktion hat ganz Allgemein die Form
\(f(x)=m\cdot x+b\)
Der Graph einer linearen Funktion ist wie der Name schon sagt eine Gerade. Dabei nennt man \(m\) die Steigung der Geraden und \(b\) nennt man den \(y\)-Achsenabschnitt, also die Stelle an der die Gerade die \(y\)-Achse schneidet. In einem Koordinantensystem wird das aussehen der Geraden, durch die Werte \(m\) und \(b\) festgelegt.
Beispiel einer linearen Funktion
Hier siehst du den Funktionsgraphen der linearen Funktion \(f(x)=2\cdot x + 1\), wobei in diesem fall \(m=2\) und \(b=1\) ist:
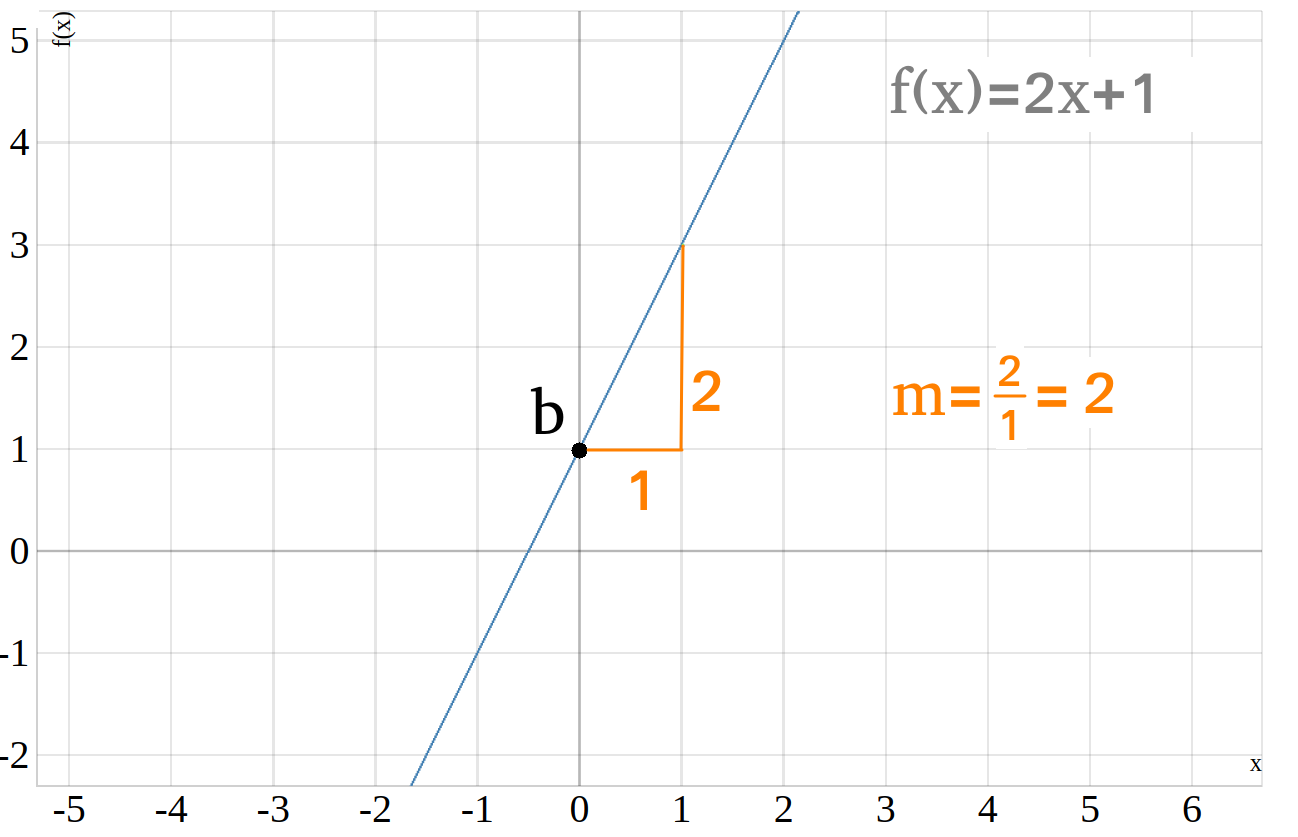
In dem obigen Graphen siehst du bereits wie man auf den Wert von \(b\) kommt, wenn dir nur der Graph gegeben ist. Dazu musst du lediglich rausfinden an welcher Stelle eine Gerade die \(y\)-Achse schneidet. Hier in diesem Fall passiert das am Punkt \((0|1)\). In einem Koordinantensystem werden Punkte immer durch die Angabe \((x|y)\) dargestellt.
Solche Graphen kannst du mit dem online Rechner für lineare Funktionen von Simplexy selber erstellen, gib in das Eingabefeld zum Beispiel \(2\cdot x + 1\) ein und siehe was passiert. Hier kommst du zum Rechner für Geraden.
Der \(y\)-Achsenabschnitt einer Geraden kann auch negativ sein, das kannst du am zweiten Beispiel sehen.
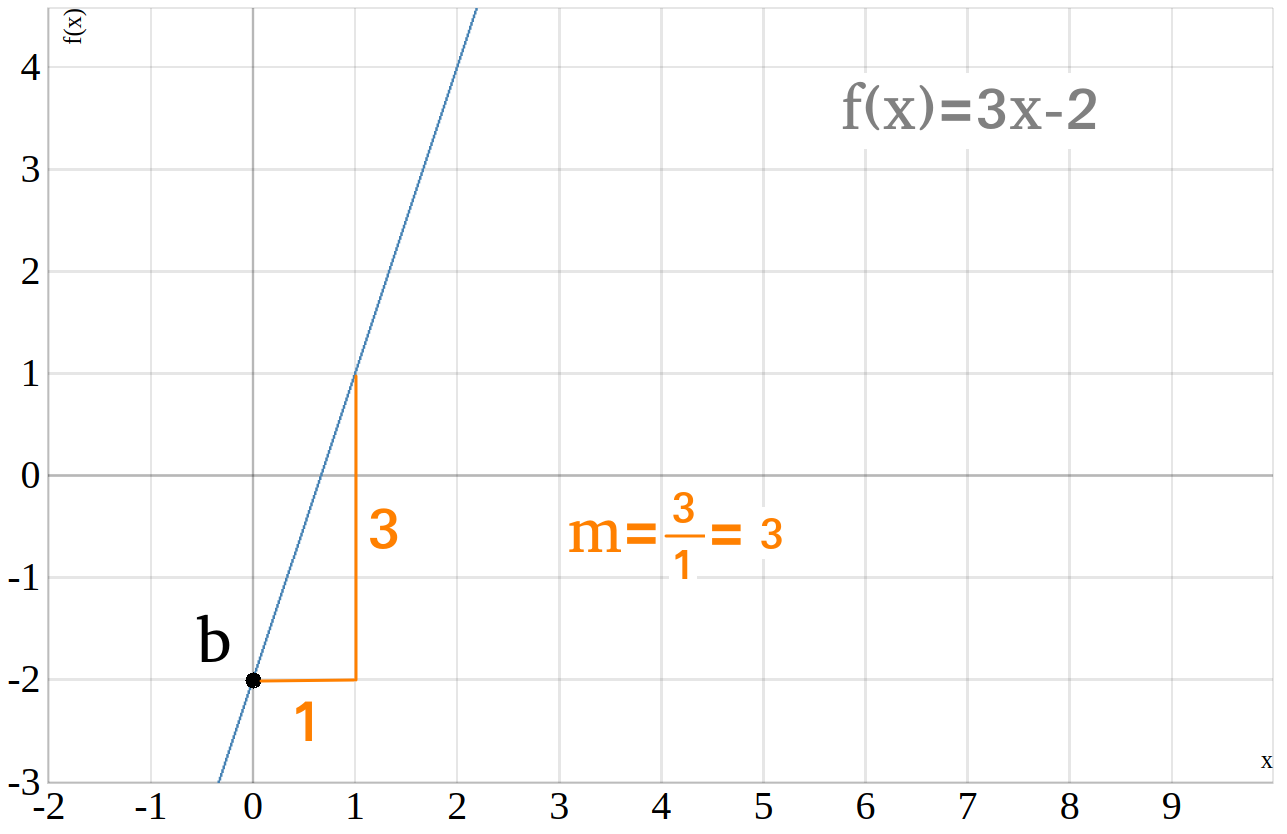
Wie du in dem Graphen oben siehst, lautet die Funktionsgleichung dieser Geraden
\(f(x)=3\cdot x - 2\).
Da die Gerade die \(y\)-Achse am punkt \((0|-2)\) schneidet, ist der \(y\)-Achsenabschnitt der Funktion \(b=-2\). Die Steigung bekommst du in dem du wieder \(\frac{\Delta y}{\Delta x}\) berechnest, also in diesem Fall \(\frac{3}{1}=3\). Damit ist die Steigung dieser Geraden \(m=3\), die Geradengleichung lautet also
\(f(x)=m\cdot x + b = 3\cdot x - 2\).
Abgesehen von einem negativen \(y\)-Achsenabschnitt kann eine lineare Funktion auch eine negative Steigung besitzen. Dazu weiter unten mehr...
Merke
In der Funktionsgleichung einer linearen Funktion steht immer nur ein \(x\). Man findet keine höhere Potenz von \(x\), zb. \(x^2\) oder \(x^3\). Eine lineare Funktion wird daher auch als Funktion ersten Grades bezeichnet.
Lineare Funktion Formel
Lineare Funktionen werden mathematisch als Geraden dargestellt. Man verwendet eine Geradengleichung um eine Lineare Funktion auszudrücken. Ganz allgemein nennt man die Gleichung einer Funktion Funktionsgleichung.
Funktionsgleichung einer linearen Funktion
Die Gleichung jeder linearen Funktion hat die Form
\(\begin{aligned} f(x)=\textcolor{blue}{m}\cdot x +\textcolor{red}{b} \end{aligned}\)
wobei \(\textcolor{blue}{m}\) die Steigung und \(\textcolor{red}{b}\) der y-Achsenabschnitt der linearen Funktion ist.
Beispiel einer linearen Funktion
Die lineare Funktion \(f(x)=\textcolor{blue}{2}\cdot x + \textcolor{red}{1}\) besitzt die Steigung \(\textcolor{blue}{2}\) und den y-Achsenabschnitt \(\textcolor{red}{1}\).
Lineare Funktion Steigung berechnen
Du siehst bereits an der Funktionsgleichung \(f(x)=2\cdot x + 1\), dass die Steigung der linearen Funktion \(m=2\) ist, doch wie findet man das heraus wenn nur der Graph gegeben ist. Das ist ganz einfach, du musst aussgehend von deinem \(y\)-Achsenabschnitt ein Quadrat bzw. eine Einheit nach rechts gehen und dann in \(y\)-Richtung solange nach oben gehen bis du deine Gerade wieder triffst. Du musst dir jetzt nur noch merken wie viele Quadrate du nach rechts und wie viele Quadrate du nach oben gegangen bist. Die Steigung bekommst du dann indem du den Quotienten
\(\begin{aligned} \frac{\Delta y}{\Delta x}=\frac{\text{Quadrate nach oben}}{\text{Quadrate nach rechts}} \end{aligned}\)
bestimmst.
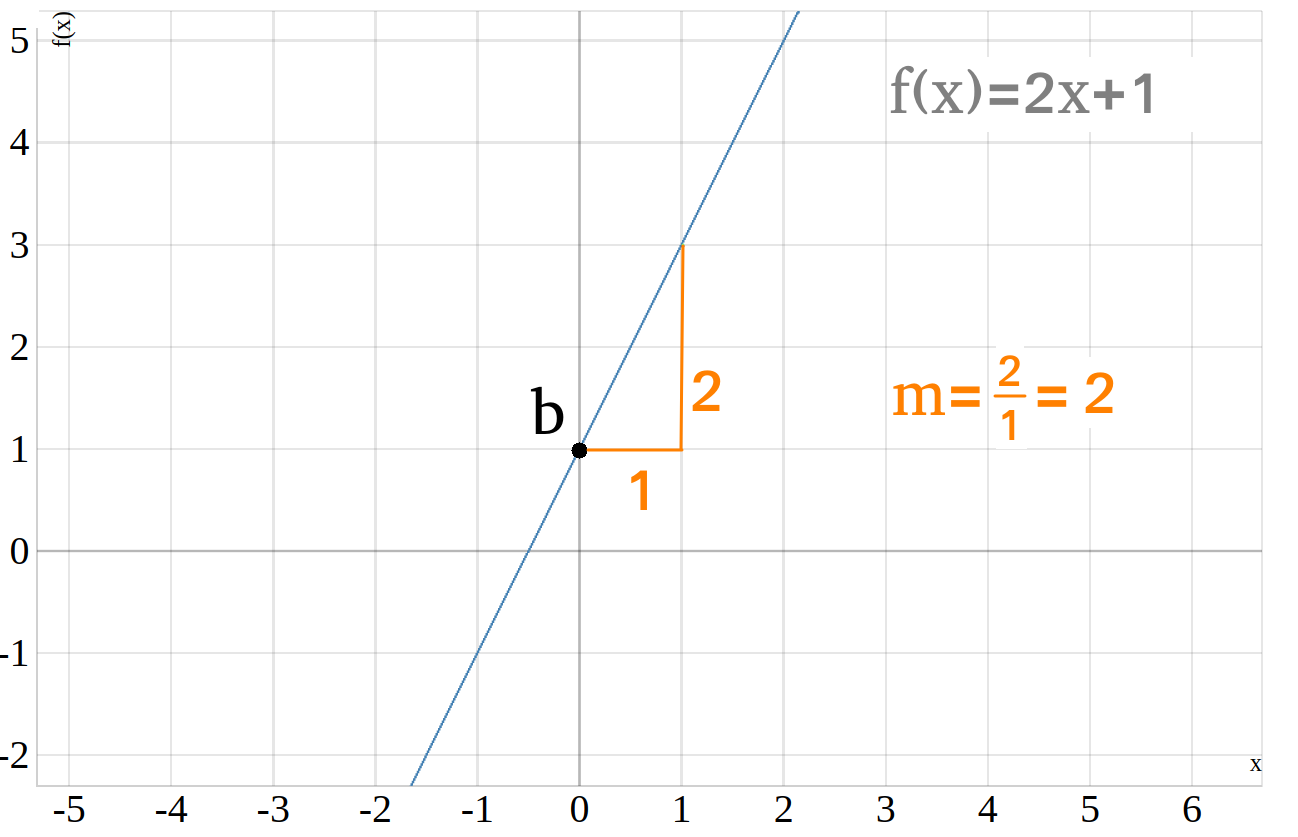
Im Beispiel von Oben gehst du ausgehend vom \(y\)-Achsenabschnitt ein Quadrat nach rechts, und dann muss man genau zwei Quadrate nach oben gehen um auf die Gerade zu treffen.
Das heißt \(\Delta x = 1\) und \(\Delta y = 2\), der Quotient \(\frac{\Delta y}{\Delta x}\) aus beiden ist also
\(\frac{2}{1}=2\).
Negative Steigung - Lineare Funktion
Hier siehst du eine Funktion mit negativer Steigung:
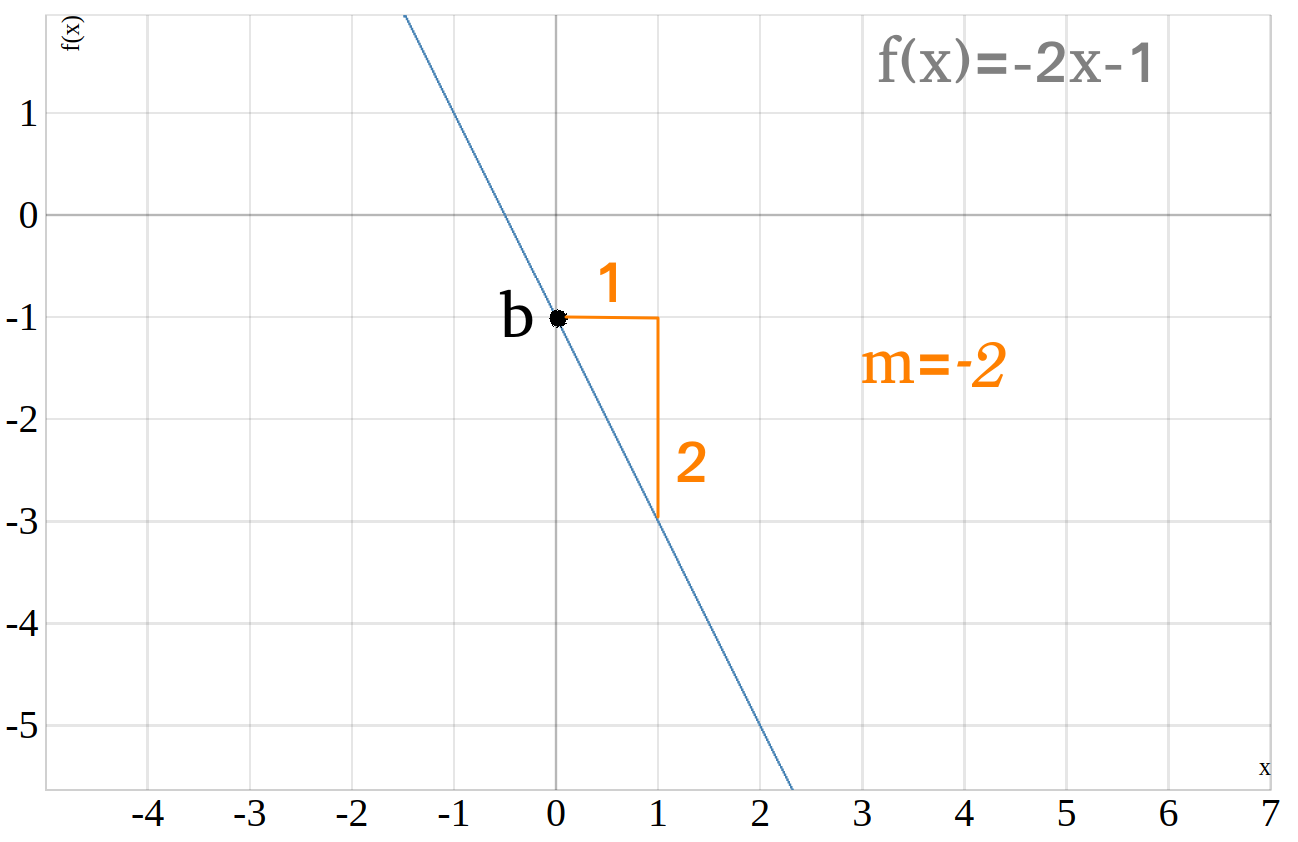
In diesem Beispiel ist die Funktion \(f(x)=-2\cdot x - 1 \), die Steigung
\(m=-2\) und der \(y\)-Achsenabschnitt \(b=-1\). Die Steigung dieser Geraden ist negativ weil die Funktion mit größeren \(x\)-Werten immer kleiner \(y\)-Werte annimmt. Anders als bei einer Funktion mit positiver Steigung ermitteln man die Steigung indem man eine Einheit nach rechts geht und dann so viele Quadrate nach unten geht bis man die Gerade wieder erreicht. Die Steigung berechnet sich bei einer linearen Funktion mit negativer Steigung folgendermaaßen
\(m=-\frac{\Delta y}{\Delta x}\).
Regel
- Der \(y\)-Achsenabschnitt ist der Punkt an dem die lineare funktion die \(y\)-Achse schneidet.
- Die Steigung einer linearen Funktion berechnet sich über \(m=\frac{\Delta y}{\Delta x}\).
- \(\Delta x\) ist die Anzahl an Einheit die man nach rechts geht. \(\Delta y\) ist die Anzahl an Einheiten die man von da aus benötigt um zur Gerade zu gelangen.
- Die Steigung ist positiv wenn man nach oben gehen muss um zur Gerade zu gelangen.
- Die Steigung ist negativ wenn man nach unten gehen muss um zur Gerade zu gelangen.
Lineare Funktion aus zwei Punkten konstruieren
Es ist möglich eine lineare Funktion und die dazu gehörige Geradengleichung aufzustellen wenn einem lediglich zwei Punkte im Koordinatensystem gegeben sind.
Nehmen wir mal an, dir sind der Punkt \(Q=(-2|-4)\) und der Punkt \(P(2|2)\) gegeben. Wie erhält man daraus die lineare Funktion, welche beide Punkte verbindet?
Zunächst einmal eine Skizze:
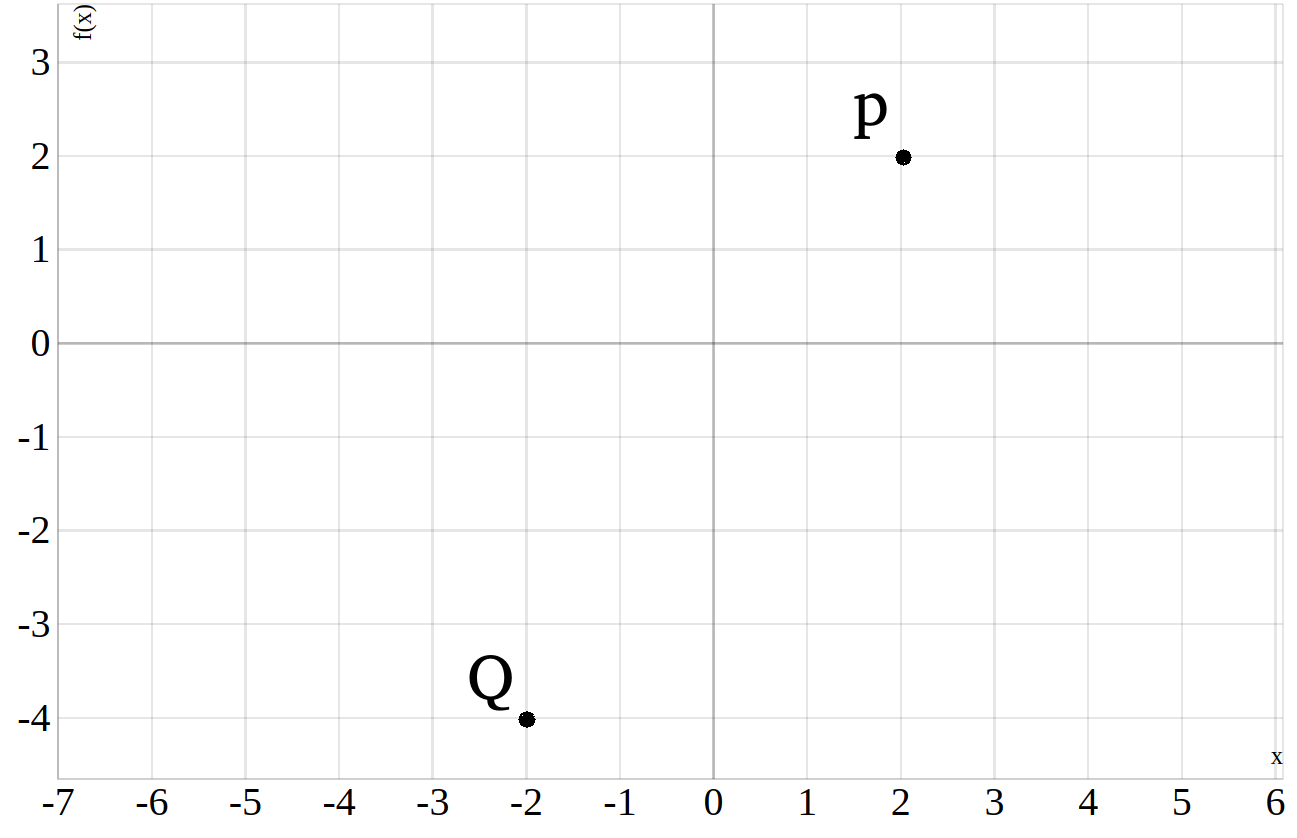
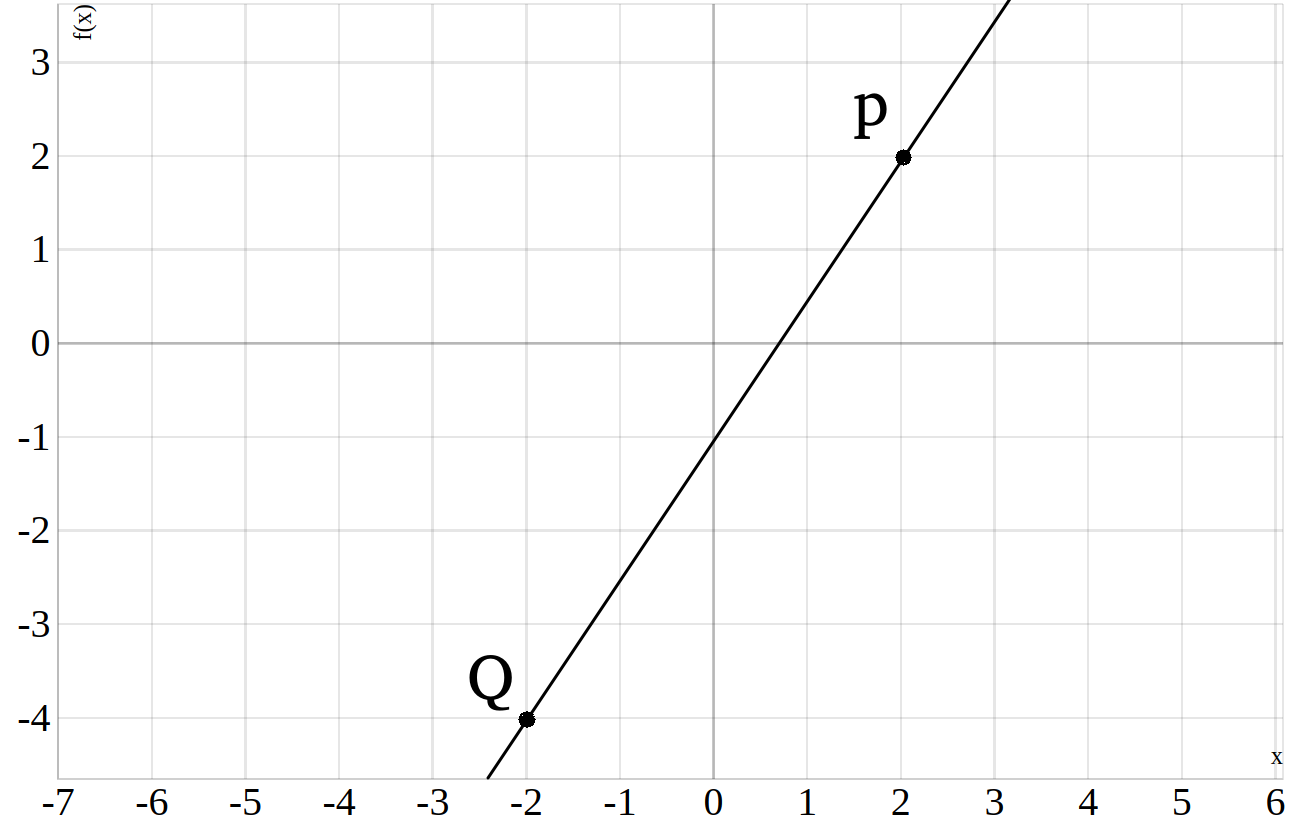
Um auf die Gerade zu kommen die durch beide Punkte \(Q\) und \(P\) geht, brauchen wir die allgemeine Geradengleichung
\(f(x)=m\cdot x+b\). Wir müssen also \(m\) und \(b\) ermitteln.
Steigung berechnen
Um die Steigung einer linearen Funktion berechnen zu können, verwenden wir die Formel:
Lineare Funktion - Steigung Formel
\(\begin{aligned} m&=\frac{\Delta y}{\Delta x}\\ \\ m&=\frac{y_2-y_1}{x_2-x_1} \end{aligned}\)
Damit erhalten wir die Steigung über die Formel:
\(\begin{aligned} m=\frac{y_Q-y_P}{x_Q-x_P} \end{aligned}\)
Wobei \(y_Q\) die \(y\)-Koordinate des Punktes \(Q\) ist und \(y_P\) ist die \(y\)-Koordinate des Punktes \(p\). Das gleiche gilt natürlich im bezug auf \(x_Q\) und \(x_P\). Setzen wir mal unsere Werte in die Gleichung ein.
\(\begin{aligned} m=\frac{-4-2}{-2-2}=\frac{-6}{-4}=\frac{3}{2} \end{aligned}\)
Es ist übrigens Egal ob man
\(\begin{aligned} m=\frac{y_Q-y_P}{x_Q-x_P} \end{aligned}\)
oder
\(\begin{aligned} m=\frac{y_P-y_Q}{x_P-x_Q} \end{aligned}\)
berechnet. Es kommt das gleiche Ergebnis bei raus, probier es mal aus.
y-Achsenabschnitt berechnen
Den \(y\)-Achsenabschnitt einer linearen Funktion erhälts du, in dem du den Punkt \(Q\) oder den Punkt \(P\) in die Geradengleichung einsetzt. Dabei ist es vollkommen egal welchen der zwei Punkte du benutzt.
Wir benutzen mal den Punkt \(Q\) und setzen \(Q=(-2|-4)\) in die Funktionsgleichung \(f(x)=m\cdot x+b\) ein. Es gilt also:
\(\begin{aligned} y&=f(x)=-4\\ \\ x&=-2\\ \\ m&=\frac{3}{2} \end{aligned}\)
Damit gilt für die Funktionsgleichung:
\(\begin{aligned} f(x)&=m\cdot x+b\\ \\ -4&=\frac{3}{2}\cdot (-2)+b \end{aligned}\)
Um auf \(b\) zu kommen müssen wir diese Gleichung jetzt nach \(b\) umformen
\(-4=\frac{3}{2}\cdot (-2)+b\,\,\,\,\,\,\,\,\,\,\,\,|-b\)
\(-4-b=-3\)
\(-4-b=-3\,\,\,\,\,\,\,\,\,\,\,\,|+4\)
\(-b=-3+4\)
\(-b=1\,\,\,\,\,\,\,\,\,\,\,\,|\cdot (-1)\)
\(\,\,\,\,\,b=-1\)
Damit haben wir nun, ausgehend von den zwei gegebenen Punkten, sowohl die Steigung \(m\) als auch den \(y\)-Achsenabschnitt berechnet. Mit Hilfe einer Skizze kannst du deine Ergebnisse immer überprüfen. Die Gerade durch die Punkte \(Q=(-2|4)\) und \(P(2|2)\) lässt sich schreiben als \(f(x)=\frac{3}{2}\cdot x - 1\).
Falls du das Umstellen einer Gleichung noch nicht gut beherrschst, oder das Lösen von Gleichungen üben möchtest, dann kannst du es hier nochmal wiederholen.
Regel:
Die Steigung einer Geraden die durch die zwei Punkte \(Q(x_Q|y_Q)\)
und \(P(x_P|y_P)\) geht, erhälts du über die Formel:Den \(y\)-Achsenabschnitt bekommst du indem du einen der Punkte \(Q(x_Q|y_Q)\) oder \(P(x_P|y_P)\) in die allgemeine Geradengleichung \(f(x)=m\cdot x+b\) einsetzt und nach \(b\) umstellst.
\(\begin{aligned} m=\frac{y_P-y_Q}{x_P-x_Q} \end{aligned}\)
Lineare Funktion Nullstelle berechnen
Was ist eine Nullstelle ?
Die Nullstelle einer linearen Funktion ist der Punkt im Koordinatensystem, an dem die Gerade die \(x\)-Achse schneidet. Um die Nullstelle zu berechnen brauchst du also lediglich die Funktionsgleichung mit Null gleichsetzen, denn gesucht ist ja der Punkt an dem die Gerade den Wert \(f(x)=0\) bzw. \(y=0\) besitzt. Versuchen wir mal die Nullstelle der Funktion \(f(x)=2\cdot x -3\) zu berechnen. Der Graph der Funktion ist unten abgebildet.
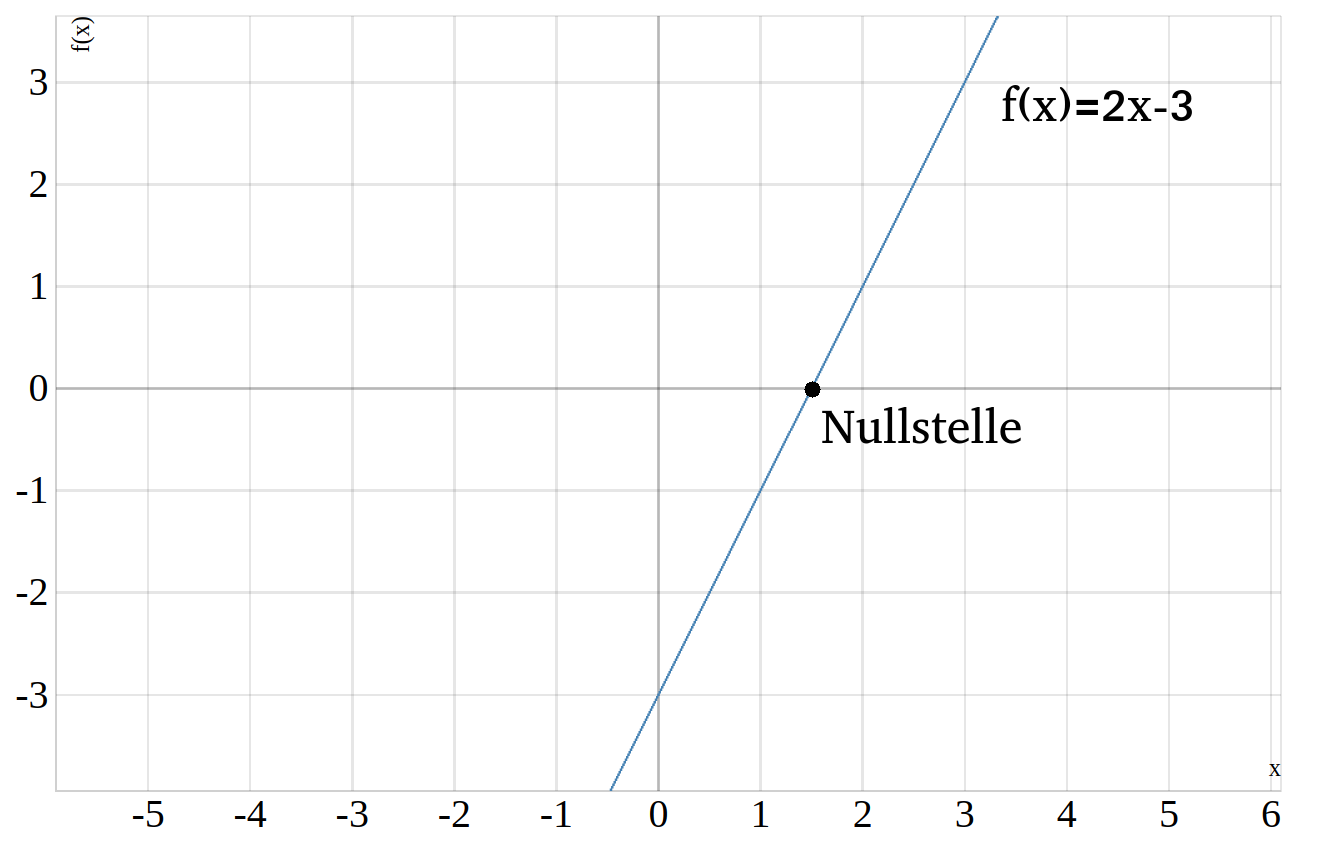
Die Nullstelle berechnest du, indem du \(0=2\cdot x -3\) nach \(x\) umstellst
\(0=2\cdot x -3\,\,\,\,\,\,\,\,\,\,\,|+3\)
\(3=2\cdot x\)
\(3=2\cdot x\,\,\,\,\,\,\,\,\,\,\,|:2\)
\(\begin{aligned} \frac{3}{2}=x \end{aligned}\)
Damit haben wir also als Nullstelle \(x=\frac{3}{2}=1,5\) ermittelt, im Graphen kann man das natürlich überprüfen.
Nullstelle berechnen - lineare Funktion
Die Nullstelle einer linearen Funktion berechnet man, indem man die Funktionsgleichung \(f(x)=m\cdot x+b\) Nullsetzt.
Dann muss man \(0=m\cdot x+b\) nach \(x\) umstellen.
Allgemein geschrieben ist die Nullstelle gegeben durch die Formel
\(\begin{aligned} x=-\frac{b}{m} \end{aligned}\)
Solche Aufgaben kannst du mit dem Online Rechner für lineare Funktionen von Simplexy lösen. Der Rechner gibt dir die Lösung und den Rechenweg an. Um die Nullstelle der Funktion \(f(x)=2\cdot x - 3\) zu bestimmt musst du im Eingabefeld \(2\cdot x -3 = 0\) eingeben, den rest erledigt der Rechner. So kannst du immer überprüfen ob du richtig gerechnest hast.
Konstante lineare Funktion
Eine lineare Funktion kann auch parallel zur \(x\)-Achse verlaufen, so eine Gerade nennt man eine Konstante. Die Funktionsgleichung einer zur \(x\)-Achse parallelen Geraden lautet \(f(x)=b\), da die Steigung \(m=0\) ist, lässt sich die Funktion also nur durch den \(y\)-Achsenabschnitt ausdrucken.
Beispiel einer konstanten Funktion \(f(x)=3\)
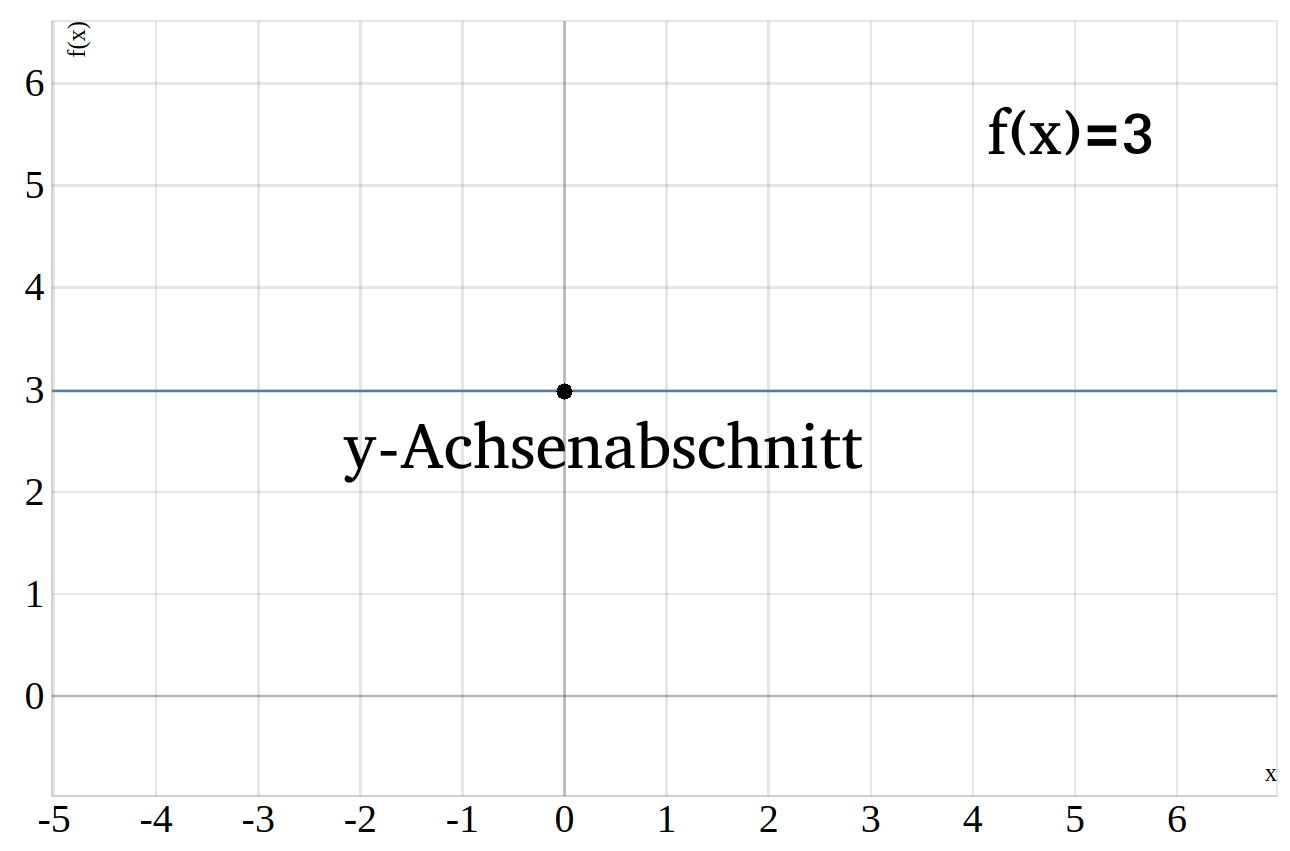
Schnittpunkt zweier Geraden
Du willst wissen wie man den Schnittpunkt zweier Geraden bzw. den Schnittpunkt zweier lineare Funktionen berechnen kann?
Dann wirf einen Blick auch den Beitrag Schnittpunkt zweier Geraden
