Schnittpunkt Lineare Funktion
Lineare Funktion Rechner
Der Online Rechner mit Rechenweg von Simplexy kann lineare Funktionen zeichnen, Nullstellen berechnen, y-Achsenabschnitt berechnen und viel mehr.
Schnittpunkt zweier Geraden berechnen
Voraussetzung
Zwei lineare Funktionen können sich nur dann schneiden, wenn sie eine unterschiedliche Steigung besitzen. Zwei Funktionen mit der gleichen Steigung verlaufen parallel zu einander und können sich daher nicht schneiden.
Die lineare Funktion \(y=2x+1\) besitzt die Steigung \(2\), genau wie die Funktion \(y=2x-2\). Beide Funktionen verlaufen daher parallel zu einander. Somit können sich diese zwei Geraden nicht schneiden.
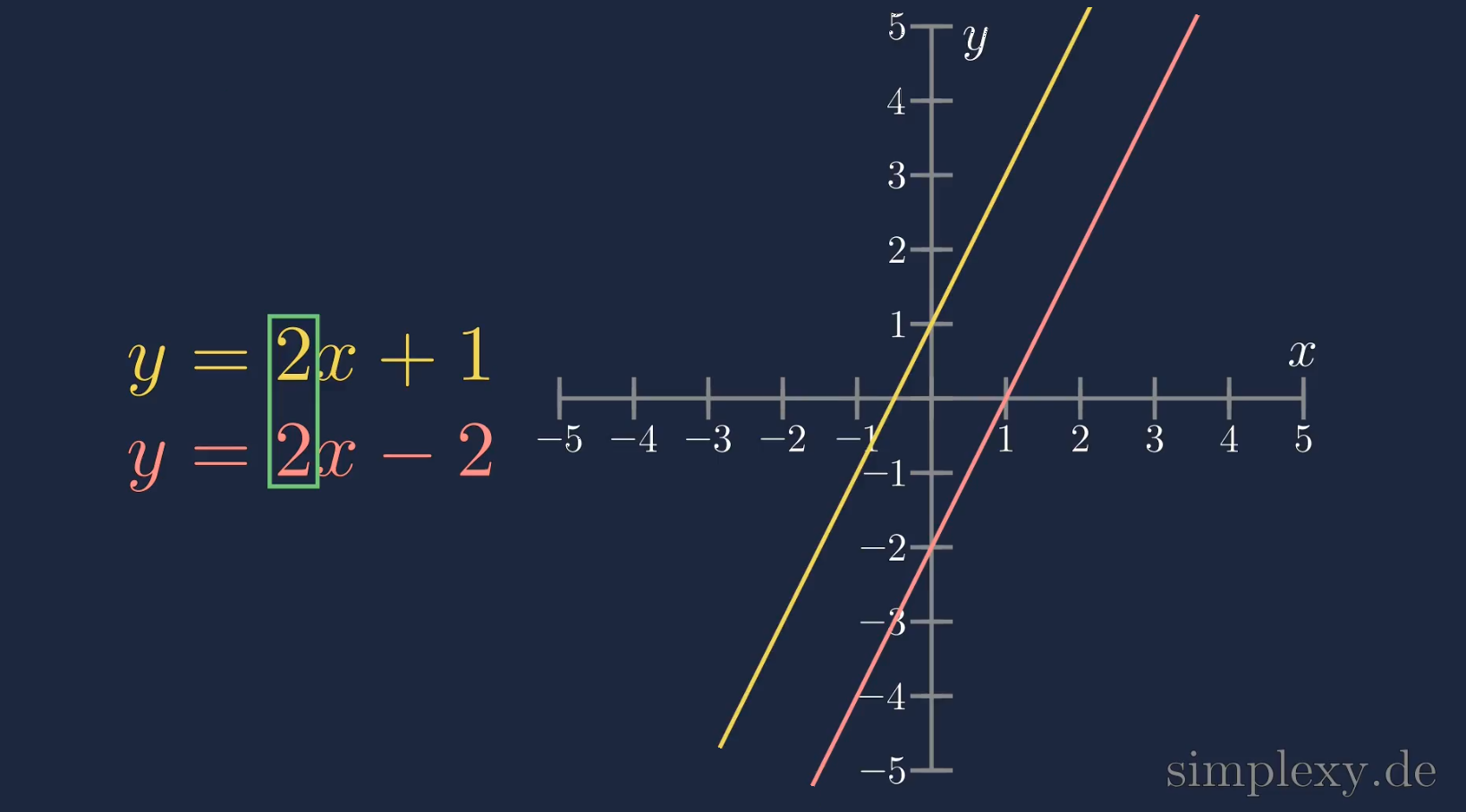
Schnittpunkt bei unterschiedlicher Steigung
Zwei lineare Funktionen mit unterschiedlicher Steigung besitzen genau einen Schnittpunkt.
Die zwei Geraden \(y_1=\frac{1}{2}x+2\) und \(y_2=3x-3\) besitzen unterschiedliche Steigungen. Beide Funktionen schneiden sich daher.
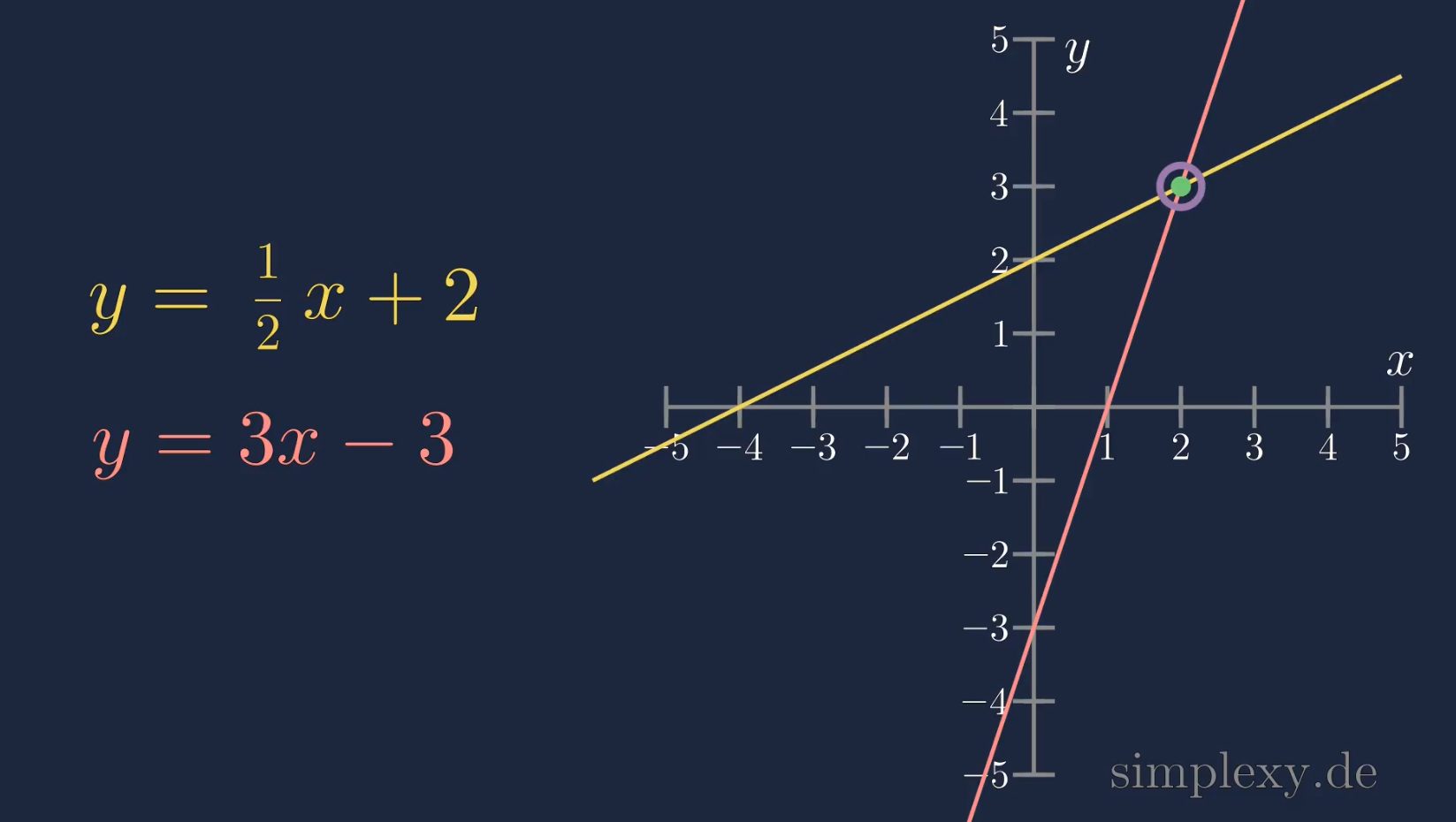
Der Schnittpunkt zweier Geraden wird durch dem \(x\)-Wert und dem dazugehörigen \(y\)-Wert angegeben. Um den \(x\)-Wert vom Schnittpunkt zu bestimmen nutzt man aus, dass beide Funktionen am Schnittpunkt den gleichen Funktionswert haben. Man kann also beide funktionen gleichsetzen und erhält:
\(\begin{aligned}y_1&=y_2\\ \frac{1}{2}x+2&=3x-3\end{aligned}\)
Durch das Gleichsetzen beider Funktionen erhlaten wir eine Gleichung die wir nach \(x\) auflösen können:
\(\frac{1}{2}x+2=3x-3\,\,\,\,\,\,\,\,\,|-3x\)
\(\frac{1}{2}x-3x+2=-3\)
\(-\frac{5}{2}x+2=-3\,\,\,\,\,\,\,\,\,\,\,\,\,\,|-2\)
\(-\frac{5}{2}x=-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,|\div 5\)
\(-\frac{1}{2}x=-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,|\cdot(-2)\)
\(x=2\)
Wir wissen nun, der \(x\)-Wert des Schnittpunktes liegt bei \(x=2\)
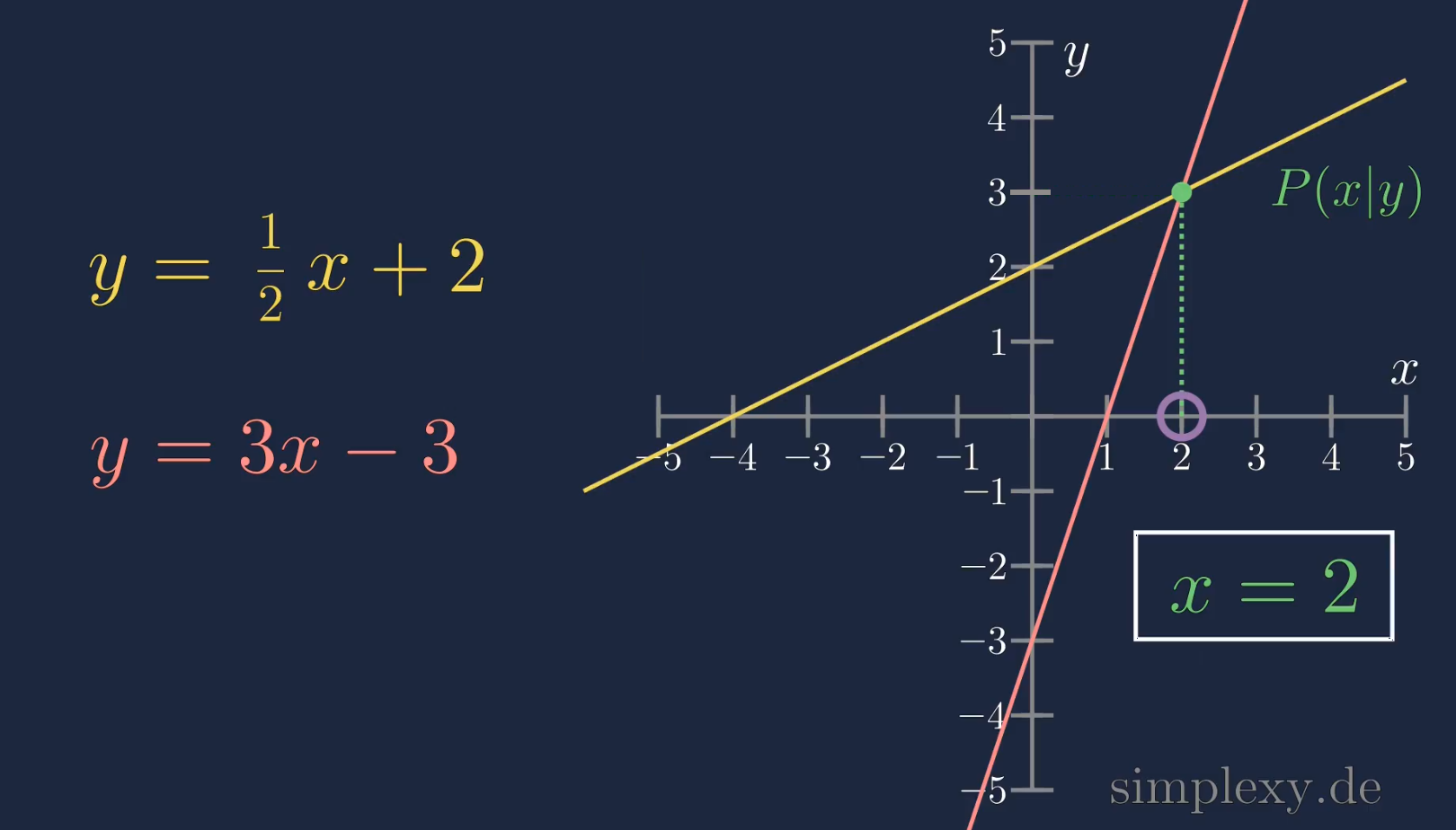
Nun fehlt nur noch der \(y\)-Wert des Schnittpunktes. Den erhalten wir, indem wir den berechneten \(x\)-Wert in eines der Funktionen einsetzen. Dabei ist es egal in welche Funktion man den \(x\)-Wert einsetzt, es sollte bei beiden Funktionen der gleich \(y\)-Wert rauskommen. Erhält man beim einsetzen in beide Funktion unterschiedliche \(y\)-Werte, so hat man bei der Berechnung des \(x\)-Wertes einen Fehler gemacht.
\(x=2\) einsetzen in \(y_1\)
\(\frac{1}{2}x+2=\frac{1}{2}\cdot 2+2=3\)
Der \(y\)-Wert des Schnittpunktes liegt bei \(y=3\).
Zur Kontrolle setzen wir den \(x\)-Wert in die zweite Funktion \(y_2\) ein:
\(3x-3=3\cdot2-3=3\)
Auch beim einsetzen in die zweite Funktion, erhalten wir für den \(y\)-Wert des Schnittpunktes \(y=3\).
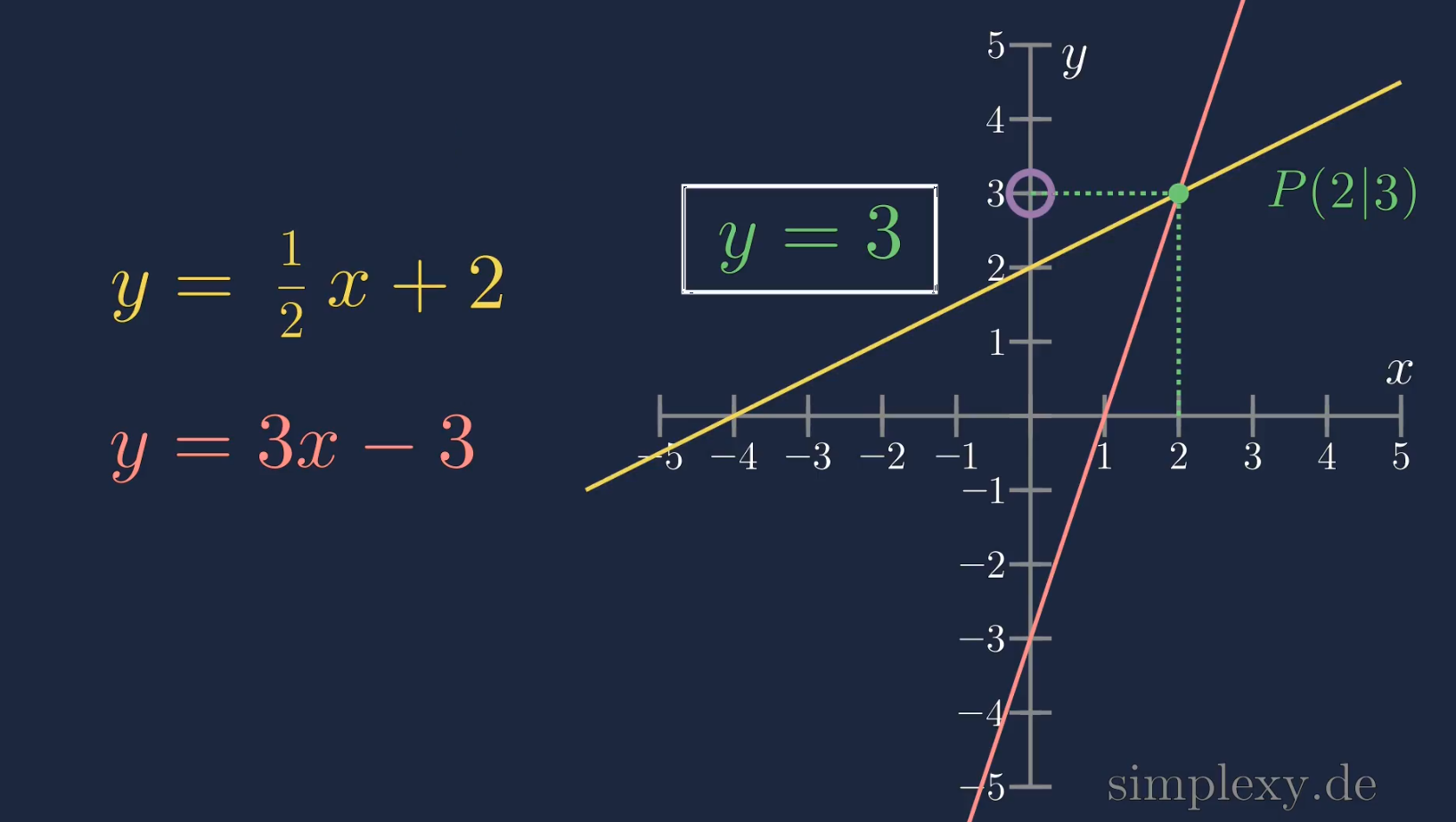
Der Schnittpunkt beider Funktion liegt damit am Punkt \((2|3)\).
Der \(x\)-Wert des Schnittpunktes muss beim Einsetzen in beide Funktionen den gleichen \(y\)-Wert ergeben. Nur dann ist der Schnittpunkt beider Funktionen bestimmt. Sollte sich beim Einsetzen vom \(x\)-Wert verschiedene \(y\)-Werte ergeben, so hast du dich wahrscheinlich verrechnet.
Lineare Funktion Schnittpunkt berechnen - Vorgehen
Setze beide linearen Funktionen gleich.
Löse die Gleichung nach \(x\) auf, um den \(x\)-Wert des Schnittpunktes zu ermitteln.
Setze den \(x\)-Wert des Schnittpunktes in einem der beiden Funktionen ein um den \(y\)-Wert des Schnittpunktes zu ermitteln
Kontrolliere den \(y\)-Wert indem du den \(x\)-Wert auch in die andere Funktion einsetzt.
Beispiel Lineare Funktion Schnittpunkt berechnen
Beispiel 1
Gesucht ist der Schnittpunkt zwischen der linearen Funktion
\(y=2\cdot x-2\) (gelb) und der Funktion
\(y=-\frac{2}{3}\cdot x+6\) (rot). Wir erkennen das beide Funktionen eine unterschiedliche Steigung besitzten, daher müssen Sie sich an einem Punkt im Koordinatensystem Schneiden.
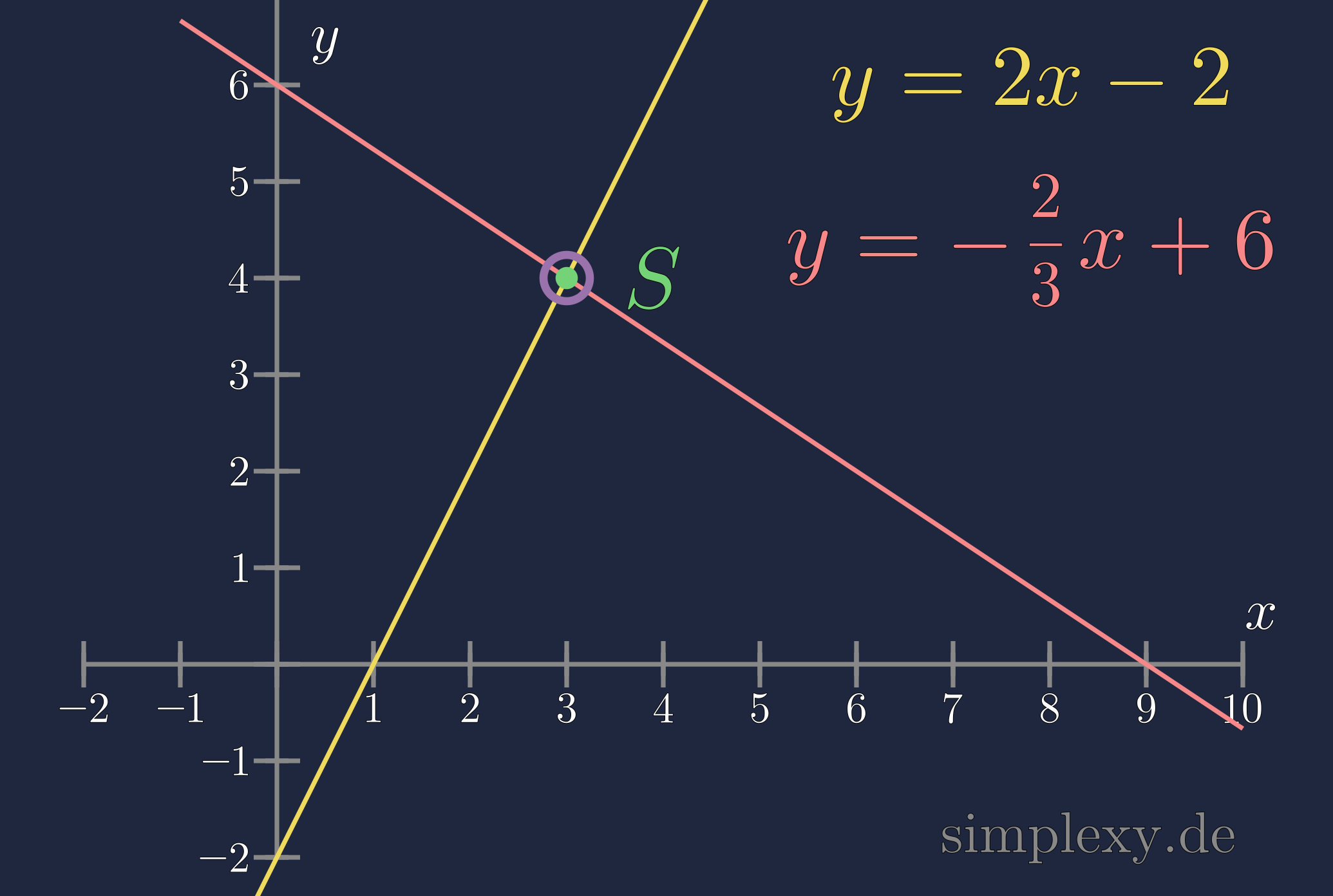
Wenn man beide Geraden in das Koordinatensystem einträgt, dann erkennt man den Schnittpunkt deutlich. Man sieht ebenfalls, dass sich dieser am Punkt \((3|4)\) befindet. Wir wollen den Schnittpunkt rechnerisch überprüfen. Dazu setzten wir beide Funktionen gleich und lösen die Gleichung nach \(x\) auf.
\(2x-2=-\frac{2}{3}x+6\,\,\,\,\,\,\,\,\,|+2\)
\(2x=-\frac{2}{3}x+8\,\,\,\,\,\,\,\,\,|+\frac{2}{3}x\)
\(\frac{8}{3}x=8\,\,\,\,\,\,\,\,\,\,\,\,\,\,|\cdot \frac{3}{8} \)
\(x=3\)
Der \(x\)-Wert des Schnittpunktes liegt also bei \(x=3\), nun benötigen wir noch den dazugehörigen \(y\)-Wert. Den erhalten wir, indem wir den \(x\)-Wert in eines der beiden Funktionen einsetzen.
Setzen wir \(x=3\) in die gelbe Funktion ein:
\(2x-2=2\cdot 3-2=4\)
Der \(y\)-Wert des Schnittpunkten scheint bei \(y=4\) zu sein. Wir können dies überprüfen, indem wir den \(x\)-Wert auch in die rote Funktion einsetzen:
\(-\frac{2}{3}x+6=-\frac{2}{3}\cdot 3+6=4\)
Auch beim einsetzen in die rote Funktion ergibt sich, dass der \(y\)-Wert des Schnittpunktes bei \(y=4\) liegt. Wir haben somit den richtigen Schnittpunkt berechnet. Der Schnittpunkt beider Funktionen liegt bei \((3|4)\).
Beispiel 2
Gesucht ist der Schnittpunkt zwischen der linearen Funktion
\(y=\frac{1}{2}\cdot x-2\) (gelb) und der Funktion
\(y=\frac{1}{2}\cdot x+\frac{4}{3}\) (rot). Wir erkennen das beide Funktionen die gleich Steigung \(\frac{1}{2}\) besitzten, daher muss es sich um parallele Funktionen handeln.
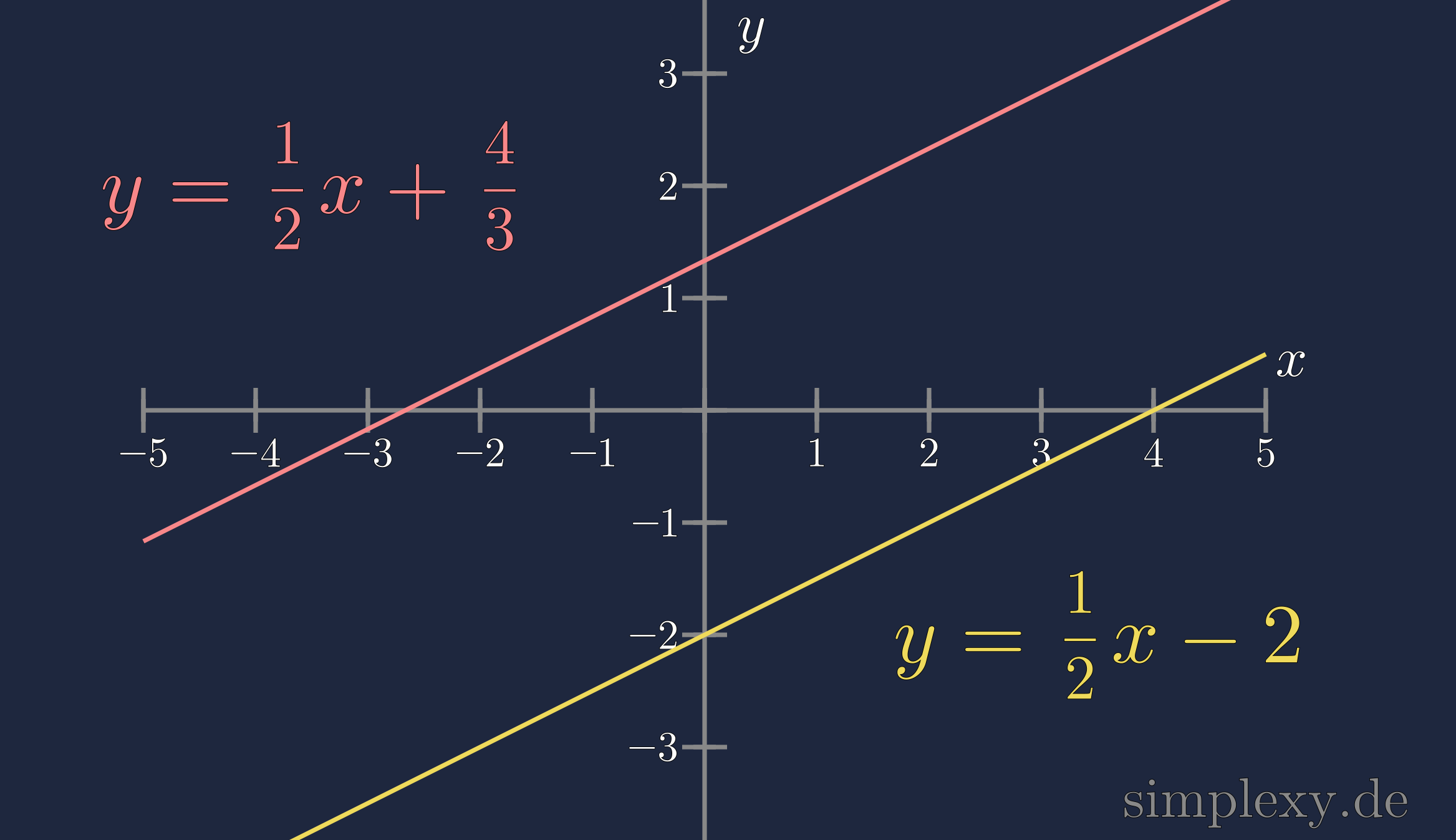
Angenommen du hast nicht bemerkt, dass beide funktionen die gleiche Steigung besitzen und du versuchst, rechnerisch den Schnittpunkt zweier Geraden zu bestimmen. Dann würdest du beide Funktionen gleichsetzen und nach \(x\) umformen:
\(\frac{1}{2}\cdot x-2=\frac{1}{2}\cdot x+\frac{4}{3}\,\,\,\,\,\,\,\,\,|-\frac{1}{2}\cdot x\)
\(-2=\frac{4}{3}\)
Das ist eindeutig ein Widerspruch, \(-2\) ist immer ungleich \(\frac{4}{3}\). In diesem Fall kannst du den Schnittpunkt zweier Funktionen nicht berechnen, weil keinen gibt.
Um sich unnötige Rechenarbeit zu ersparen, loht es sich die Steigung beider Funktionen zu vergleichen.
Lineare Funktionen Schnittpunkt berechnen - Vorgehen
Gegeben seien die Funktionen:
\(f(x)=m\cdot x+b\)
\(g(x)=n\cdot x+t\)
Vorgehen, Schnittpunkt zweier Linearer Funktionen berechnen:
Schritt 1: Betrachte beide Funktionen sehr genau und finde raus ob sie die gleiche Steigung besitzen. Das erkennt man daran, dass \(m=n\) ist. Man könnte auch beide Funktionen in ein Koordinatensystem eintagen und die Steigung über ein Steigungsdreieck ermitteln. Haben beide Funktionen die gleiche Steigung, so sind sie parallel. Sollten beide Funktionen unterschiedliche \(y\)-Achsenabschnitte besitzen, also \(b\neq t\), so haben sie keinen Schnittpunkt.
Schritt 2: Haben beide Funktionen unterschiedliche Steigungen (\(m\neq n\)), so haben sie einen eindeutigen Schnittpunkt. Die Koordinaten dieses Schnittpunktes kann man leicht berechen, man beginnt damit den \(x\)-Wert des Schnittpunktes zu ermitteln. Dazu setzt man beide Funktionen gleich und stellt nach \(x\) um.
Schritt 3: Setze den berechneten \(x\)-Wert des Schnittpunktes in einem der beiden Funktionen ein, um den zugehörigen \(y\)-Wert zu erhalten.
Schritt 4: Um sicherzugehen, dass du den richtigen Schnittpunkt hast, musst du den \(x\)-Wert auch in die andere Funktion einsetzen. Wenn auch da, der gleichen \(y\)-Wert raus kommt, hast du richtig gerechnet. Es sollte beide Male das gleiche für den \(y\)-Wert rauskommen.
\(m\cdot x+b=n\cdot x+t\)
\(\rightarrow \text{nach } x\text{ umstellen}\)
Schnittpunkte Mögliche Ergebnisse
Es gibt drei mögliche Ergebnisse, bei Schnittpunkten von linearen Funktionen:
Die Geraden haben keinen Schnittpunkt. Dann sind die Geraden Parallel und sie besitzen die gleiche Steigung, zudem haben beide Funktionen unterschiedliche y-Achsenabschnitte.
Die Geraden schneiden sich in einem Punkt. Der Punkt ist eindeutig und seine Koordinaten können durch das Gleichsetzen der beiden Funktionen ermittelt werden.
Die Geraden haben unendlich viele Schnittpunkte. Das ist der Fall, wenn beide Funktionen identisch sind. In anderen Worten, beide Funktionen liegen auf einander.
