Klammerrechnung
Online Rechner mit Rechenweg
Mit dem Online Rechner von Simplexy kannst du viele Matheaufgaben berechnen und dabei den Rechenweg erhalten.
Rechnen mit Klammern
In diesem Kapitel werden einige der wichtigsten Rechenregeln besprochen, behandelt werden die Rechenregeln für Klammern. Klammersetzung spielt in der Mathematik eine wichtige Rolle, die Klammern geben die Priorität vor. Im Allgemeinen werden Operationen innerhalb einer Klammer zuerst gelöst, erst im Anschluss führt man die weiteren Rechenoperationen durch. So ähnlich wie bei der Punkt vor Strichrechnung weis man durch die Klammern in einer Gleichung wo man anfangen soll. Am Ende dieses Kapitels wirst du wissen wie Klammer ausmultiplizieren funktioniert, wie Klammerlösen geht und wie du die Klammerrechnung mit Brüchen am einfachsten verstehst.
Mit dem Klammer Rechner von Simplexy kannst du beliebige Klammeraufgaben lösen und überprüfen.
Klammerrechnung leicht erklärt
Die Klammern in einer Gleichung geben die Priorität der Rechenoperationen vor. Klammern haben eine höhere Priorität als die Punkt vor Stichregel.
Klammerrechnung
Immer erst was innerhalb der Klammern steht ausrechnen dann weiter den Rest berechnen.
Beispiele zur Erklärung
- \(\textcolor{blue}{(2+3)}\cdot 4=\textcolor{blue}{5}\cdot 4=20\)
- \(5\cdot \textcolor{blue}{(1+4)}=5\cdot \textcolor{blue}{5}=25\)
- \(2\cdot \textcolor{blue}{(1+3)}+5=2\cdot \textcolor{blue}{4}+5=8+5=13\)
-
\(\begin{aligned} \frac{\textcolor{blue}{(6+4)}}{2}+1=\frac{\textcolor{blue}{10}}{2}+1=5+1=6 \end{aligned}\)
- \(\textcolor{blue}{(1+4)}\cdot \textcolor{red}{(1+1)}=\textcolor{blue}{5}\cdot \textcolor{red}{2}=10\)
In dem ersten Beispiel \(\textcolor{blue}{(2+3)}\cdot 4=5\cdot 4=20\) muss aufgrund der Klammer erst \(\textcolor{blue}{(2+3)}=\textcolor{blue}{5}\) gerechnet werden und danach
\(\textcolor{blue}{5}\cdot 4=20\). Die Klammer hat also die Punkt vor Strichrechnung aufgehoben, Klammern haben also eine höhere Priorität. Mit Klammern zu rechnen ist sehr einfach, man muss zuerst alles innerhalb einer Klammer ausrechnen und anschließend alles weitere berechnen.
Auch im vierten Beispiel \(\frac{\textcolor{blue}{(6+4)}}{2}+1\) wird zuerst was in der Klammer steht gelöst. Im Zähler steht \(\textcolor{blue}{(6+4)}\) das wird gelöst und man erhätt die \(\textcolor{blue}{10}\). Diese \(\textcolor{blue}{10}\) schreibt man in den Zähler \(\frac{\textcolor{blue}{10}}{2}+1\) und dann kann man anschließend wie gehabt weiter rechnen.
Mehrere Klammern auflösen
Wie kann man mehrere Klammern auflösen ?
Am besten wird es mit einpaar weiteren Beispielen deutlich
- \(\textcolor{blue}{(2+3)}+\textcolor{green}{(5+1)}=\textcolor{blue}{5}+\textcolor{green}{6}=11\)
- \(\textcolor{blue}{\big(}\textcolor{green}{(1+3)}+6\textcolor{blue}{\big)}+5=\textcolor{blue}{\big(}\textcolor{green}{4}+6\textcolor{blue}{\big)}+5=15\)
- \(\textcolor{blue}{(1+3)}\cdot \textcolor{green}{(2+4)}+4=\textcolor{blue}{4}\cdot \textcolor{green}{6}+4=28\)
- \(\textcolor{blue}{\bigl(}\textcolor{green}{(1+4)}+3\textcolor{blue}{\bigr)}\cdot2=\textcolor{blue}{(}\textcolor{green}{5}+3\textcolor{blue}{)}\cdot 2=\textcolor{blue}{8}\cdot 2=16\)
Im ersten Beispiel hat man zwei Klammern die durch ein \(+\) getrennt sind, hier ist es mathematisch egal welche Klammer zuerst gelöst wird. Im zweiten Beispiel werden innere Klammern durch äußere Klammer umgeben \(\bigl((1+3)+6\bigr)\). In so einem Fall ist es wichtig erst die innerste Klammer zu rechnen \((1+3)=4\) und im Anschluss die äußere Klammer \(\bigl(4+6\bigr)=10\) zu berechnen.
Beim dritten Beispiel \((1+3)\cdot (2+4)+4\), sind zwei Klammern durch eine Multiplikation getrennt. Auch hier macht es keinen Unterschied welche der beiden Klammern zuerst gelöst wird, man sollte aber stets von link nach rechts rechnen. Also löst man zuerst
\((1+3)=4\) und danach \((2+4)=6\), dann kann man den Rest berechnen \(4\cdot 6+4=28\).
Rechnen mit mehreren Klammern
Beim Rechnen mit mehreren Klammer gilt: Erst die innerste Klammer lösen und sich dann nach außen hin arbeiten.
Wenn du diese Regel beachtest ist das Rechnen mit Klammern sehr leicht. Trotzallem wird man erst durch das Üben besser, versuche die folgenden Aufgaben zu Lösen. Um deine Ergebnisse zu überprüfen oder eine Schritt für Schritt Erklärung zu bekommen kannst du die Aufgaben im Rechner von Simplexy eingeben.
Klammerrechnung Aufgaben
- \((1+5)\cdot 2=\)
- \(3\cdot (1+4)=\)
- \(2\cdot (2+1)+5=\)
- \((\frac{(6+2)}{2}+1)-2=\)
- \(\bigl(2\cdot (2+3)+5\bigr)\cdot 2=\)
Klammer ausmultiplizieren
Wie kann man eine Klammer ausmultiplizieren?
Um eine Klammer ausmultiplizieren zu Können, muss nach der Klammer direkt eine Multiplikation stehten.
Beispiel

- \((2+2)\cdot 4=(8+8)=16\)
Man Könnte aber auch so rechnen wie wir es im letzten Abschnitt getan haben.
- \((2+2)\cdot 4=4\cdot 4=16\)
Es macht also mathematisch keinen unterschied ob man
\((2+2)\cdot 4=(2\cdot 4+2\cdot 4)=8+8=16\) oder
\((2+2)\cdot 4=4\cdot 4=16\) rechnet
Man kann also entweder die Klammer zuerst Lösen und dann weiter rechnen oder man zieht die \(4\) in die Klammer und rechnet dann weiter.
Im Algemeinen gelten folgende Regeln:
- \((a+b)\cdot c=a\cdot c+b\cdot c\)
- \(c\cdot (a+b)=a\cdot c+b\cdot c\)
Wenn in der Klammer ein Produkt steht und nicht ein Plus dann ist es noch einfacher.
Es gilt dann:
- \((a\cdot b)\cdot c=a\cdot b \cdot c\)
- \(c\cdot (a\cdot b)=a\cdot b \cdot c\)
Hier einpaar Beispiele:
- \((2+3)\cdot 2=5\cdot 2=10\)
- \(\bigl((1+2)\cdot 2\bigr)\cdot 3=(3\cdot 2)\cdot 3 =3\cdot 2\cdot 3=18\)
- \((2\cdot 2)\cdot 5=4\cdot 5=20\)
- \(\bigl((3\cdot 2)\cdot 1\bigr)\cdot 2=(6\cdot 1)\cdot 2 =6\cdot 2=12\)
Klammer mal Klammer ausmultiplizieren
Jetzt kann man sich die Frage stellen wie Klammer mal Klammer ausmultiplizieren funktioniert.
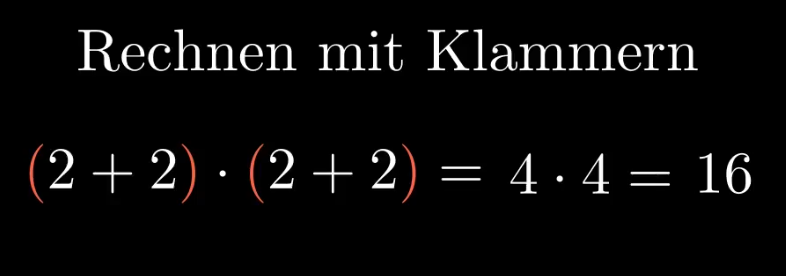
Auch hier gilt das man jede Klammer für sich löst und dann beide Ergebnise mit einander Multipliziert.
Beispiel:
- \((2+3)\cdot (1+4)=5\cdot 5=25\)
Man kann also jede Klammer für sich Lösen und dann die Multiplikation beider Ergebnise miteinander berechnen.
Das gleiche Ergebnis bekommt man auch wenn man folgendermaßen rechnet:
- \((2+3)\cdot (1+4)=2\cdot 1+2\cdot 4+3\cdot 1+3\cdot 4=25\)
Im Algemeinen gilt die Regel:
\((a+b)\cdot (c+d)=a\cdot c+a\cdot d+b\cdot c+b\cdot d\)
Minus vor der Klammer
Wie kann man ein Minus vor der Klammer auflösen? Betrachten wir mal zur Erklärung das nächste Beispiel.
Beispiel
- \(-(2+3)\cdot 2=-5\cdot 2=-10\)
Hier wurde wieder zuerst das was in der Klammer steht berechnet, das Minus schreiben wir einfach vor dem Ergebnis
\(-(2+3)=-5\). Anschießen kann man wie gehabt
\(-5\cdot 2=-10\) Rechnen.
Das Minus vor der Klammer kann man sich wie eine -1 vorstellen,
\(-(2+3)=-1\cdot (2+3) = -1\cdot 5 = -5\)
Im Allgemeinen gilt die Regel:
\(-(a+b)\cdot c=-1\cdot (a+b)\cdot c\)
\(=(-a-b)\cdot c=-a\cdot c-b\cdot c\)
Klammerrechnung mit Brüchen
Enthalten deine Klammer auch Brüche, so kannst du auch da die gleichen Rechenregeln verwenden, die du oben gelernt hast.
<
Klammer mit Bruch auflösen
- Klammern zuerst ausrechnen. Wenn mehrere Klammern vorhanden sind, rechnest du von innen nach außen.
- Punkt vor Strichrechnung.
- Von Links nach Rechts Rechnen.
Beispiel für Klammerrechnung mit Brüchen:
\(\bigl(\frac{1}{4}\cdot (\frac{1}{2}+\frac{1}{2})\bigr)+\frac{1}{4}\)\(=\frac{1}{4}\cdot 1+\frac{1}{4}=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}\)
\(\frac{(3+1)}{2}\cdot 4=\frac{(3\cdot 4+1 \cdot 4)}{2}\)\(=\frac{(12+4)}{2}=\frac{16}{2}=8\)
\(\frac{\frac{3}{4}}{\frac{4}{5}}-(\frac{1}{4}+\frac{1}{2})=\frac{\frac{3}{4}}{\frac{5}{4}}-(\frac{1}{4}+\frac{2}{4})\)\(=\frac{15}{16}-\frac{3}{4}=\frac{15}{16}\cdot \frac{12}{16}=\frac{3}{16}\)
\(\frac{(\frac{3}{5}\, -\,\frac{4}{10})}{(\frac{4}{30}\, -\,\frac{2}{15})}=\frac{(\frac{6}{10}-\frac{4}{10})}{(\frac{2}{15}+\frac{2}{15})} \)\(=\frac{\frac{2}{10}}{\frac{4}{15}}=\frac{2}{10}\cdot \frac{15}{4}\)
\(=\frac{1}{5}\cdot \frac{15}{4}=\frac{1}{1}\cdot \frac{3}{4}=\frac{3}{4}\)
