Scheitelpunkt
Scheitelpunkt Rechner
Mit dem Parabelrechner von Simplexy kannst du ganz einfach die Nullstellen einer quadratischen Funktion berechnen, eine Parabel zeichnen lassen, ein Scheitelpunkt berechnen uvm.
Was ist der Scheitelpunkt einer Parabel?
Scheitelpunkt Definition
Der Scheitelpunkt einer Parabel ist der höchste oder tiefste Punkt einer Parabel.
Eine quadratischen Funktion kann über zwei Arten ausgedrückt werden. Es gibt die Normalform einer Parabel und es gibt die Scheitelpunktform einer Parabel. Jede quadratische Funktion kann in beiden Formen angegeben werden. Hat man eine quadratische Funktion in der Normalform gegeben, so kann man diese umwandeln in die Scheitelpunktform. Eine Umwandlung von der Scheitelpunktform in die Normalform ist ebenfalls möglich. Das Aussehen der Parabel ist unabhängig davon wie man die quadratische Funktion angibt, es sind ledigleich zwei verschiebene Schreibweisen für die gleiche Parabel.
Normalform und Scheitelpunktform einer quadratischen Funktion
Scheitelpunktform
\(f(x)=a(x+d)^2+e\)
Normalform
\(f(x)=ax^2+bx+c\)
Scheitelpunkt ablesen
Der Vorteil der Scheitelpunktform (oft auch Scheitelform genannt) liegt darin, dass man den Scheitelpunkt einer Parabel ablesen kann.
Scheitelpunkt einer Parabel ablesen
Die Scheitelpunktform einer quadratischen Funktion lautet:
Scheitelpunktform
\(f(x)=a(x\textcolor{blue}{+}\textcolor{red}{d})^2\textcolor{green}{+e}\)
Die Koordinaten vom Scheitelpunkt kann man direkt ablesen. Der Scheitelpunkt befindet sich bei:
\(S(\textcolor{blue}{-}\textcolor{red}{d}|\textcolor{green}{e})\)
Achtung!
Ein \(\textcolor{blue}{+}\textcolor{red}{d}\) in der Scheitelpunktform führt dazu das der x-Wert vom Scheitelpunkt bei \(\textcolor{blue}{-}\textcolor{red}{d}\) liegt. Hier ist es mit den Vorzeichen genau umgekehrt. Mehr dazu im Video und in den Beispielen...
Parabel Scheitelpunkt Beispiele
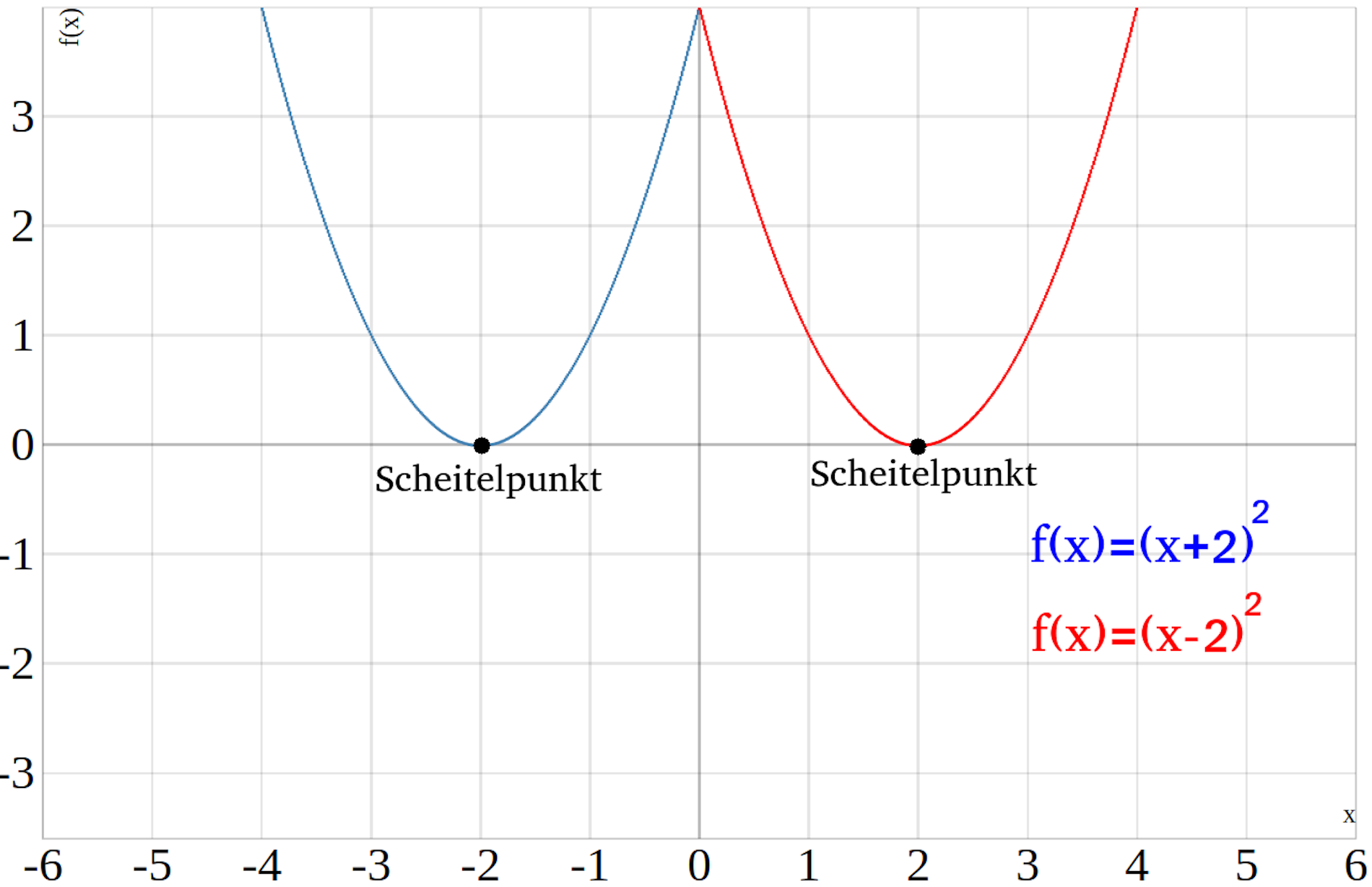
Im unteren Bild ist der Scheitelpunkt einer nach links verschobenen Parabel (blau) und einer nach rechts verschobenen Parabel (rot) dargestellt.
Beispiel 1
Gegeben ist die folgende quadratische Funktion in der Scheitelpunktform.
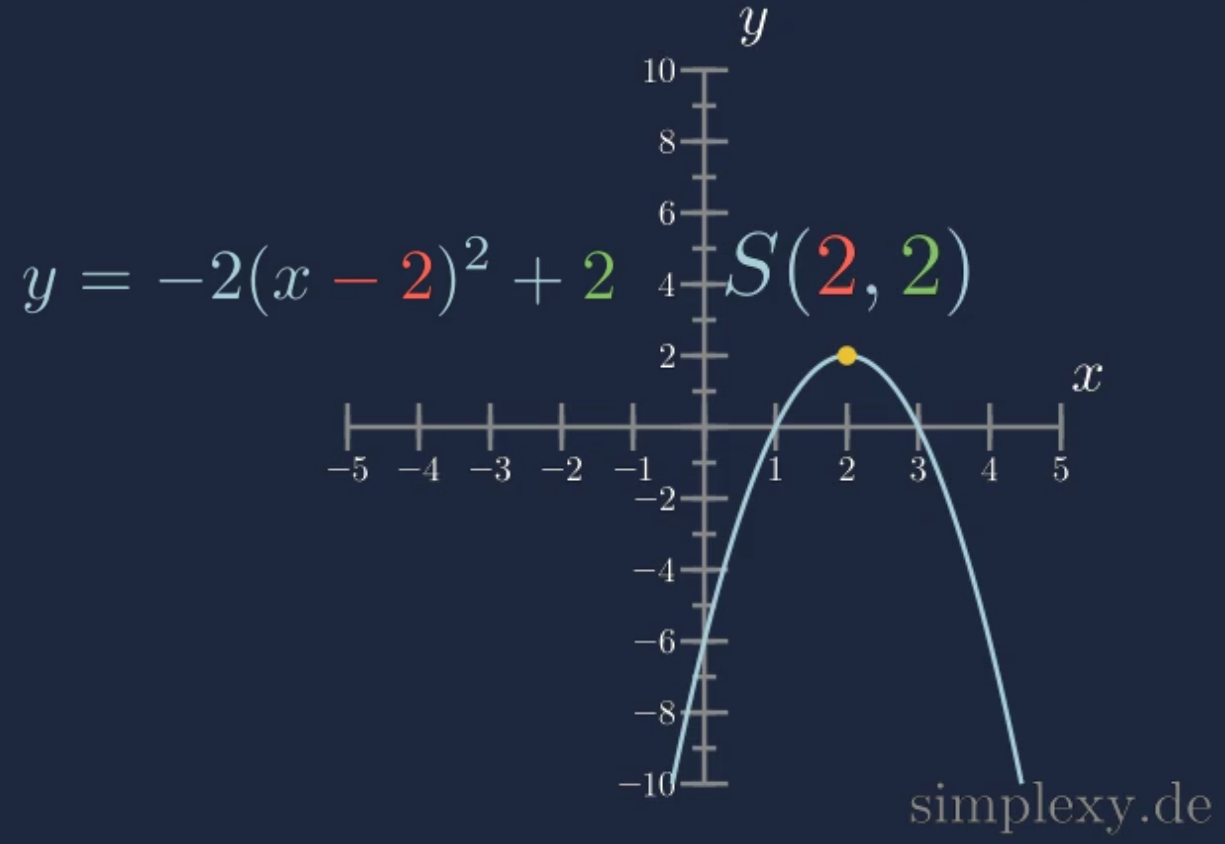
\(f(x)=-2(x\textcolor{blue}{-}\textcolor{red}{2})^2\textcolor{green}{+2}\)
Wie lauten die Koordinaten vom Scheitelpunkt?
Man kann den Scheitelpunkt ablesen, die Koordinaten vom Scheitelpunkt \(S\) liegen bei:
\(S(\textcolor{red}{2}|\textcolor{green}{2})\)
In der folgenden Abbildung ist die Funktion und der Scheitelpunkt dargestellt:
Beispiel 2
Gegeben ist die Parabel:
\(f(x)=(x\textcolor{blue}{+}\textcolor{red}{1})^2\)
Wo liegt der Scheitelpunkt?
Man kann den Scheitelpunkt aus der Scheitelpunktform ablesen:
\(S(\textcolor{red}{-1}|0)\)
Im folgenden Video ist die Funktion und der Scheitelpunkt dargestellt.
Beispiel 3
Gegeben ist die folgende quadratische Funktion:
\(f(x)=\frac{1}{2}x^2\textcolor{green}{-4}\)
Wie lauten die Koordinaten vom Scheitelpunkt?
Man kann die Koordinaten vom Scheitelpunkt ablesen:
\(S(\textcolor{red}{0}|\textcolor{green}{-4})\)
In der folgenden Abbildung ist die Parabel und der Scheitelpunkt dargestellt.
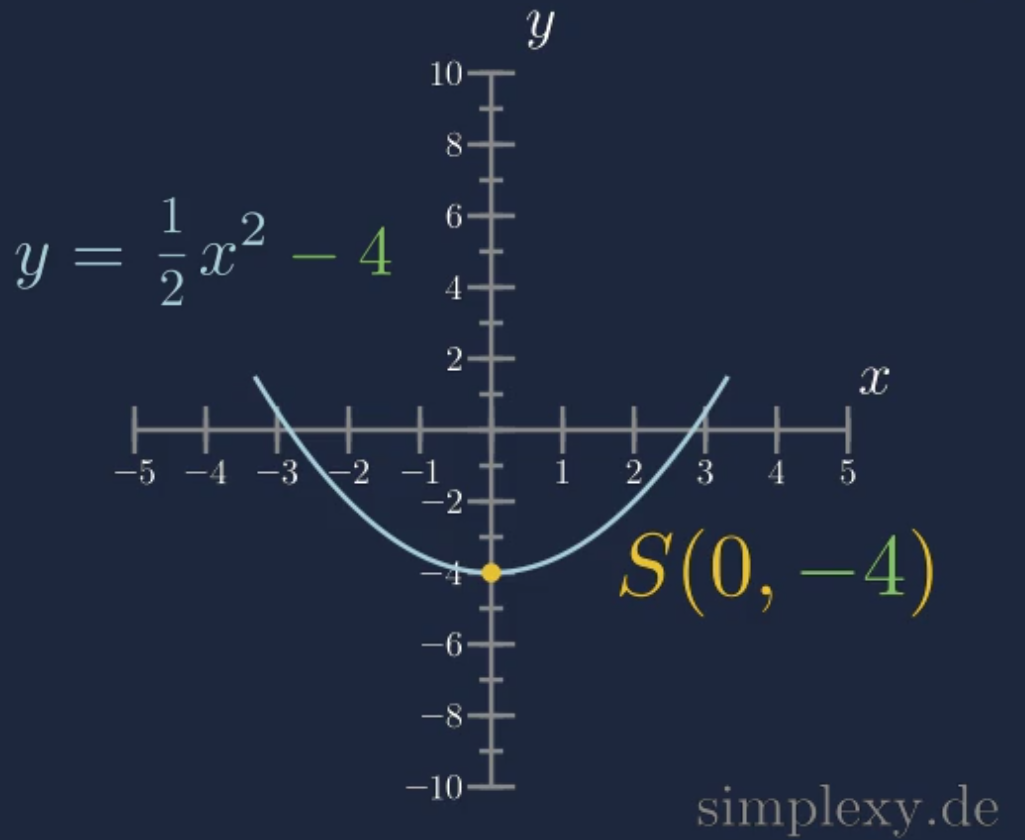
Scheitelpunkt Normalform
Wie bereits erwähnt muss eine quadratische Funktion nicht in der Scheitelpunktform angegeben werden. Eine quadratischen Funktion kann auch über die Normalform ausgedrückt werden. Dabei handelt es sich nur um eine andere Schreibweise zur Scheitelpunktform. Man kann zwischen der Scheitelpunktform und der Normalform hin und her wechseln.
Im allgemeinen wird eine quadratische Funktion in der Normalform über
\(f(x)=ax^2+bx+c\)
ausgedrückt. Der unterschied zur Scheitelpunktform liegt an dem Term \(bx\). Über die Normalform kann man die Koordinaten des Scheitelpunktes nicht direkt ablesen. Hier muss man den Scheitelpunkt berechnen.
Normalform einer Parabel
\(f(x)=ax^2+bx+c\)
Scheitelpunkt berechnen
Um den Scheitelpunkt berechnen zu können, benötigt man eine Formel. Für eine quadratische Funktion der Form:
\(f(x)=ax^2+bx+c\)
befindet sich der Scheitelpunkt bei den Koordninaten:
\(\begin{aligned} S=\Big(\,\,\,\frac{-b}{2a}\,\,\,\Big|\,\,\,\frac{4ac-b^2}{4a}\,\,\,\Big) \end{aligned}\)
Scheitelpunkt Formel
Der Scheitelpunkt einer quatradischen Funktion der Form
\(f(x)=ax^2+bx+c\)
berechnet sich über
\(S=\Big(\,\,\,\frac{-b}{2a}\,\,\,\Big|\,\,\,\frac{4ac-b^2}{4a}\,\,\,\Big)\)
Beispiel Scheitelpunkt berechnen
Beispiel 4
Die Funktion
\(f(x)=-2x^2+8x-6\)
ist eine Parabel in der Normalform, die gleiche Parabel in der Scheitelpunktform lautet:
\(f(x)=-2(x-2)^2+2\)
Sie ist die Parabel aus Beispiel 1. Verwende die Formel für den Scheitelpunkt einer Parabel um die Koordinaten vom Scheitelpunkt zu berechnen. Vergleiche das Ergebnis mit dem Scheitelpunkt aus Beispiel 1.
Lösung
Der Scheitelpunkt berechnet sich über die Formel:
\(S(\,\,\,\frac{-b}{2a}\,\,\,|\,\,\,\frac{4ac-b^2}{4a}\,\,\,)\)
Die gegebene Funktion lautet:
\(f(x)=-2x^2+8x-6\)
Damit ist \(a=-2\), \(b=8\) und \(c=-6\). Die Werte können nun in die Scheitelpunkt Formel eingesetzt werden.
\(\begin{aligned} S&=(\,\,\,\frac{-8}{-2\cdot 2}\,\,\,|\,\,\,\frac{4\cdot 2\cdot 6-8^2}{-4\cdot 2}\,\,\,)\\ \\ S&=(2|2) \end{aligned}\)
Genau wie in Beispiel 1 befindet sich der Scheitelpunkt bei \(S(2|2)\). Es handelt sich bei der Funktion \(f(x)=-2x^2+8x-6\) und \(f(x)=-2(x-2)^2+2\) um die gleiche Parabel, nur einmal in der Normalform und einmal in der Scheitelpunktform ausgedürckt.
