Sinus, Cosinus und Tangens - Winkelfunktionen
Winkelfunktion Rechner
Simplexy besitzt einen Online Rechner mit Rechenweg. Probier den Rechner aus !
Winkelfunktionen
In diesem Kapitell wirst du lernen wie man mit Sinus, Cosinus und Tangens die Winkel und Seitenlängen in einem rechtwinkligen Dreieck berechnet. Du wirst Begriffe wie Hypotenuse, Ankathete und Gegenkathete nutzen, du solltest dich am besten schon etwas mit der Geometrie des Dreiecks beschäftigt haben. Das kannst du hier wiederholen, wenn nötig. Mit dem Online Rechner von Simplexy kannst du viele Aufgaben berechnen, du erhälts bei vielen Aufgaben auch einen Lösungsweg. Hier kommst du zum online Rechner.
Die Trigonometrie ist eine Lehre, die sich mit Längen und Winkeln in Dreiecken beschäftigt.
In der Mathemathik bezeichnet man Winkelfunktionen auch als trigonometrische Funktionen.
Wiederholung
Ein Dreieck mit einem rechten Winkel heißt rechtwinkliges Dreieck. Die Hypotenuse ist die längste Seite eines rechtwinkligen Dreiecks, sie liegt immer gegenüber vom rechten Winkel. Man bezeichnet die zwei kürzeren Seiten als Kathete. Die Winkeln in einem Dreieck werden mit griechischen Buchstaben gekennzeichnet.
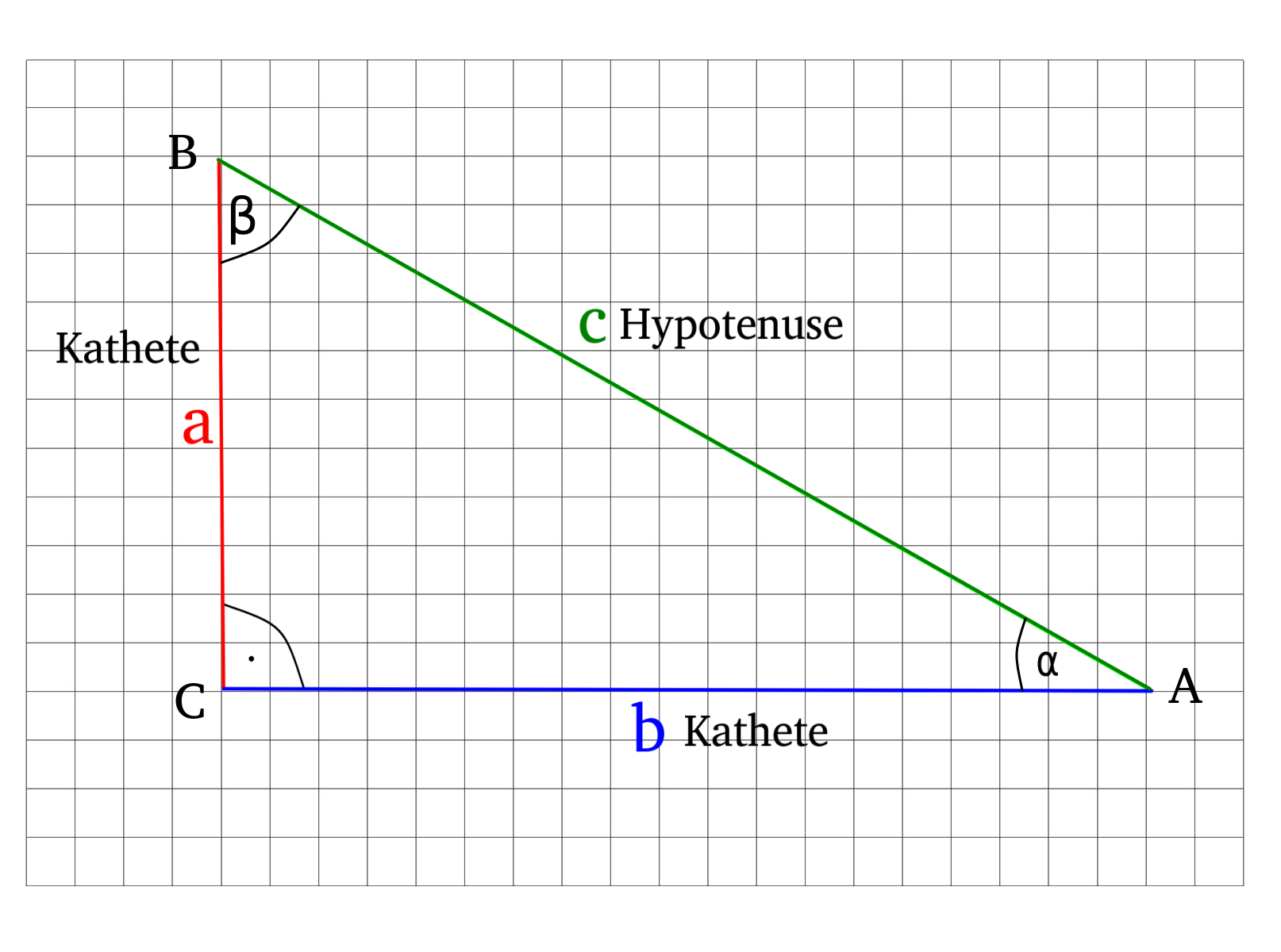
Um die zwei Katheten zu unterscheiden verwendet man die Begriffe Ankathete und Gegenkathete. Welches der zwei man Gegenkathete und welches man Ankathete nennt, hängt immer davon ab auf welchen Winkel man die Katheten bezieht. In den nächsten zwei Bildern wird das verdeutlicht.
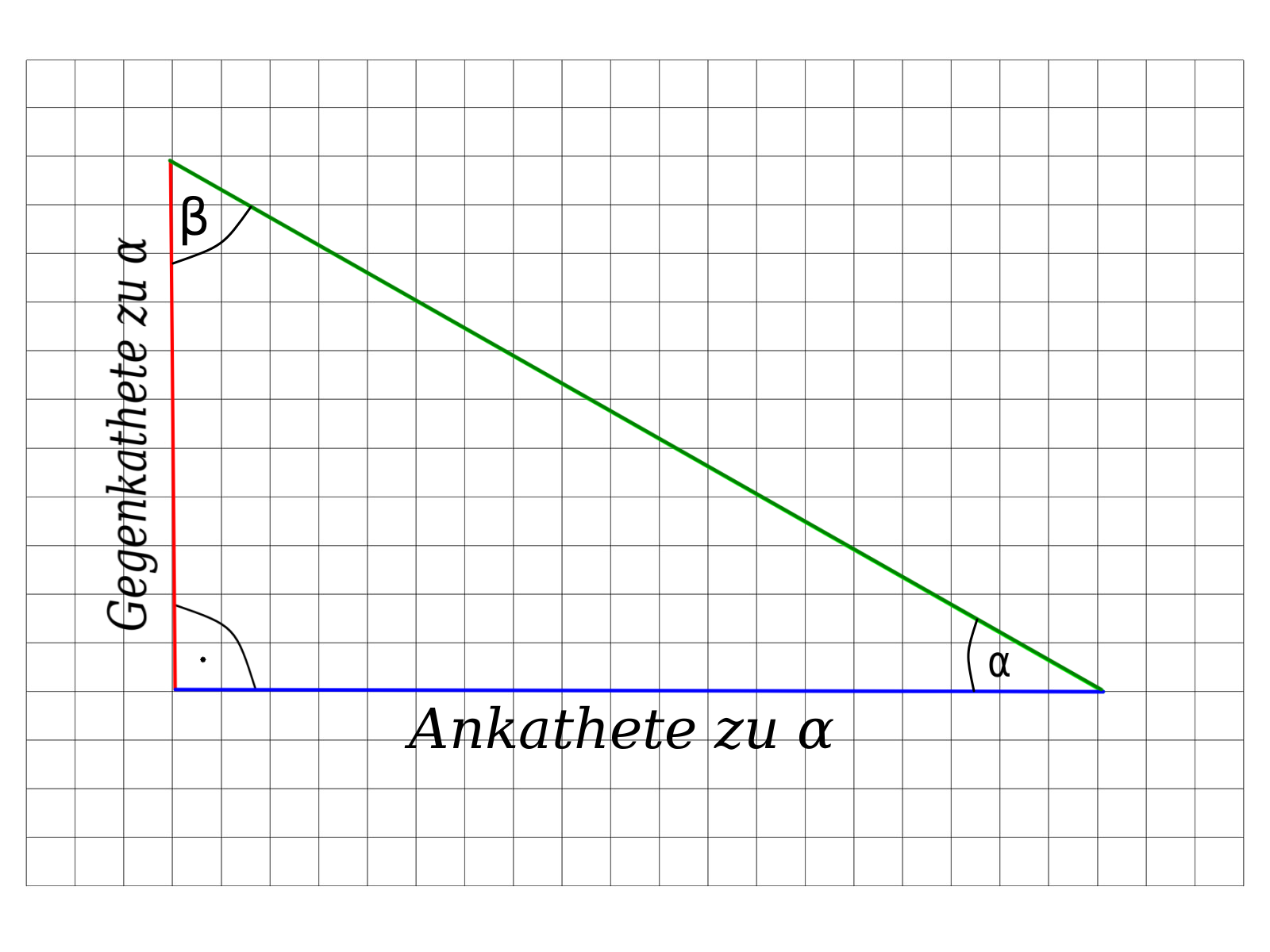
In der oberen Abbildung, siehst du das die rote Seite gegenüber vom Winkel \(\alpha\) liegt, deswegen wird die rote Seite auch Gegenkathete zu \(\alpha\) genannt. Die rote Seite liegt aber auch gleichzeitig an dem Winkel \(\beta\) weshalb diese Seite gleichzeitig die Ankathe zu \(\beta\) ist. Das siehst du im unteren Bild.
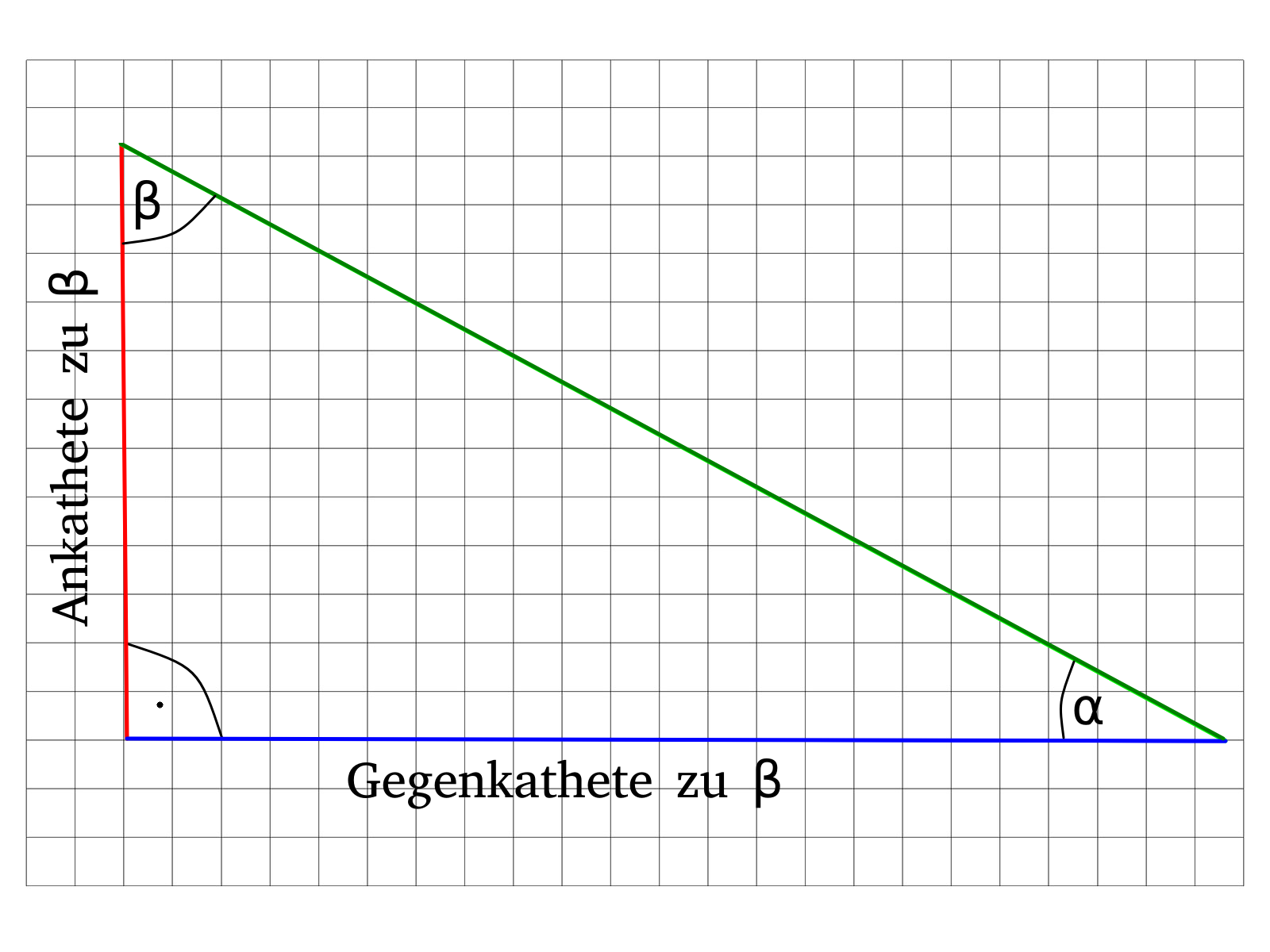
Dir sollte nun aufgefallen sein das beide Katheten sowohl eine Ankathe als auch eine Gegenkathe sind, es kommt nur darauf an, auf welchen Winkel man sich bezieht. Die Begriffe Ankathete und Gegenkathete bekommen also erst ein Bedeutung wenn man zusätzlich erwähnt auf welchen Winkel man sich bezieht.
Regel:
- Die dem Winkel anliegende Kathete heißt Ankathete
- Die dem Winkel gegenüberliegende Kathete heißt Gegenkathete
Wir beziehen und ab jetzt auf den Winkel \(\alpha\) und veruschen zu lernen wie man mit dem Sinus, Cosinus und dem Tangens umgeht.
Mit den Funktionen Sinus, Cosinus und Tangens kann man das Verhältnis zweier Seiten in einem rechtwinkligen Dreieck berechnen. Doch wie genau geht das ?
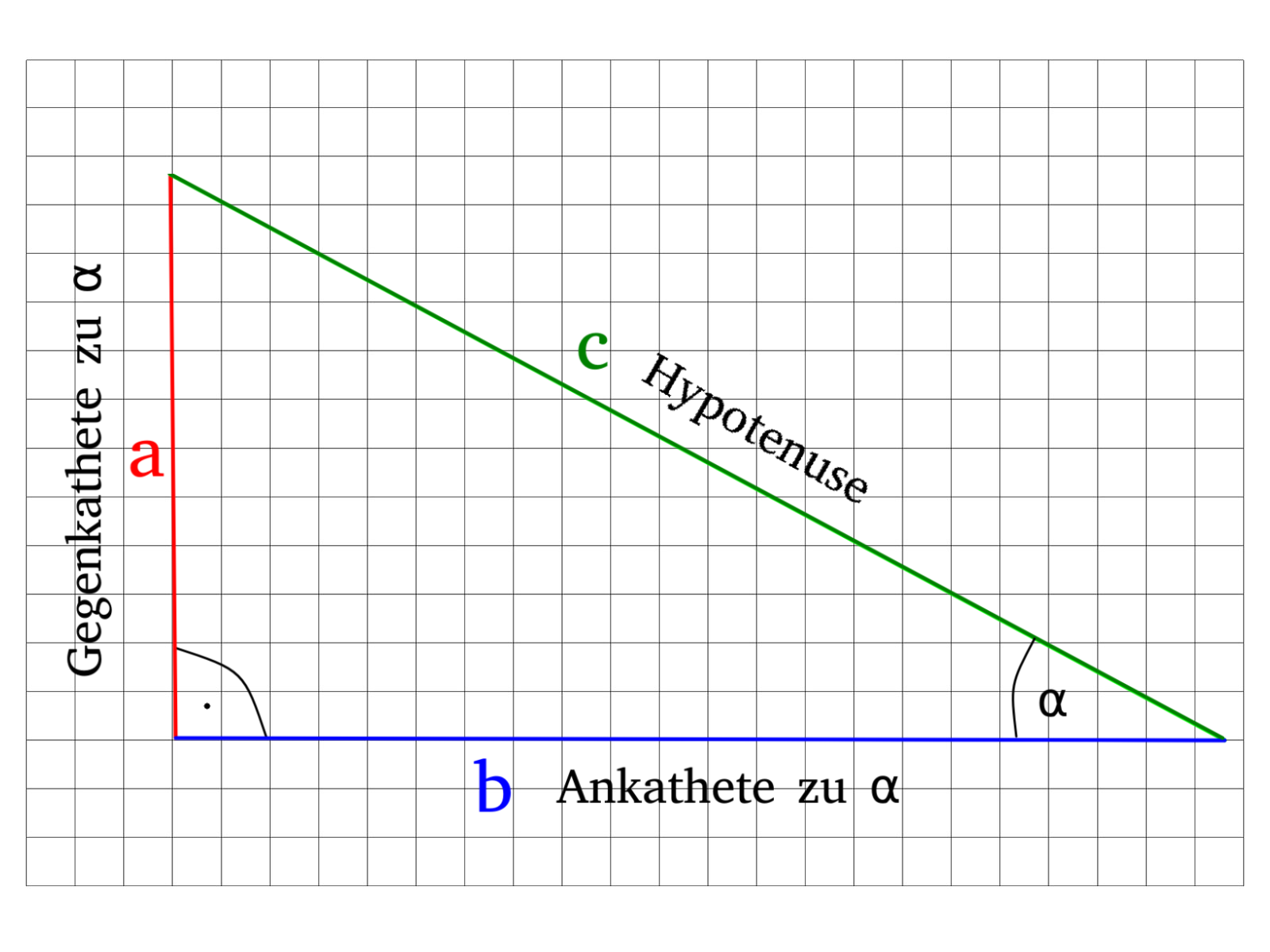
Wir benutzen zur Definition der Winkelfunktionen die obere Abbildung. Dabei steht der Winkel \(\alpha\) im Fokus.
Im Bezug auf den Winkel \(\alpha\), ist die Seite \(a\) die Gegenkathete und die Seite \(b\) die Ankathete. Also gilt:
- Die Seite \(a\) ist die Gegenkathete zu \(\alpha\)
- Die Seite \(b\) ist die Ankathete zu \(\alpha\)
- Die Seite \(c\) ist die Hypotenuse
Regel:
Der Sinus des Winkels \(\alpha\) entspricht dem Verhältnis von Gegenkathete zu Hypotenuse
\(sin(\alpha)=\)\(\frac{Gegenkathete}{Hypotenuse}=\frac{a}{c}\)
Regel:
Der Cosinus des Winkels \(\alpha\) entspricht dem Verhältnis von Ankathete zu Hypotenuse
\(cos(\alpha)=\)\(\frac{Ankathete}{Hypotenuse}=\frac{b}{c}\)
Regel:
Der Tangens des Winkels \(\alpha\) entspricht dem Verhältnis von Gegenkathete zu Ankathete
\(tan(\alpha)=\)\(\frac{Gegenkathete}{Ankathete}=\frac{a}{b}\)
Beispiel 1
Gegeben ist das folgende Dreieck, berechne die Länge der Seite \(a\).
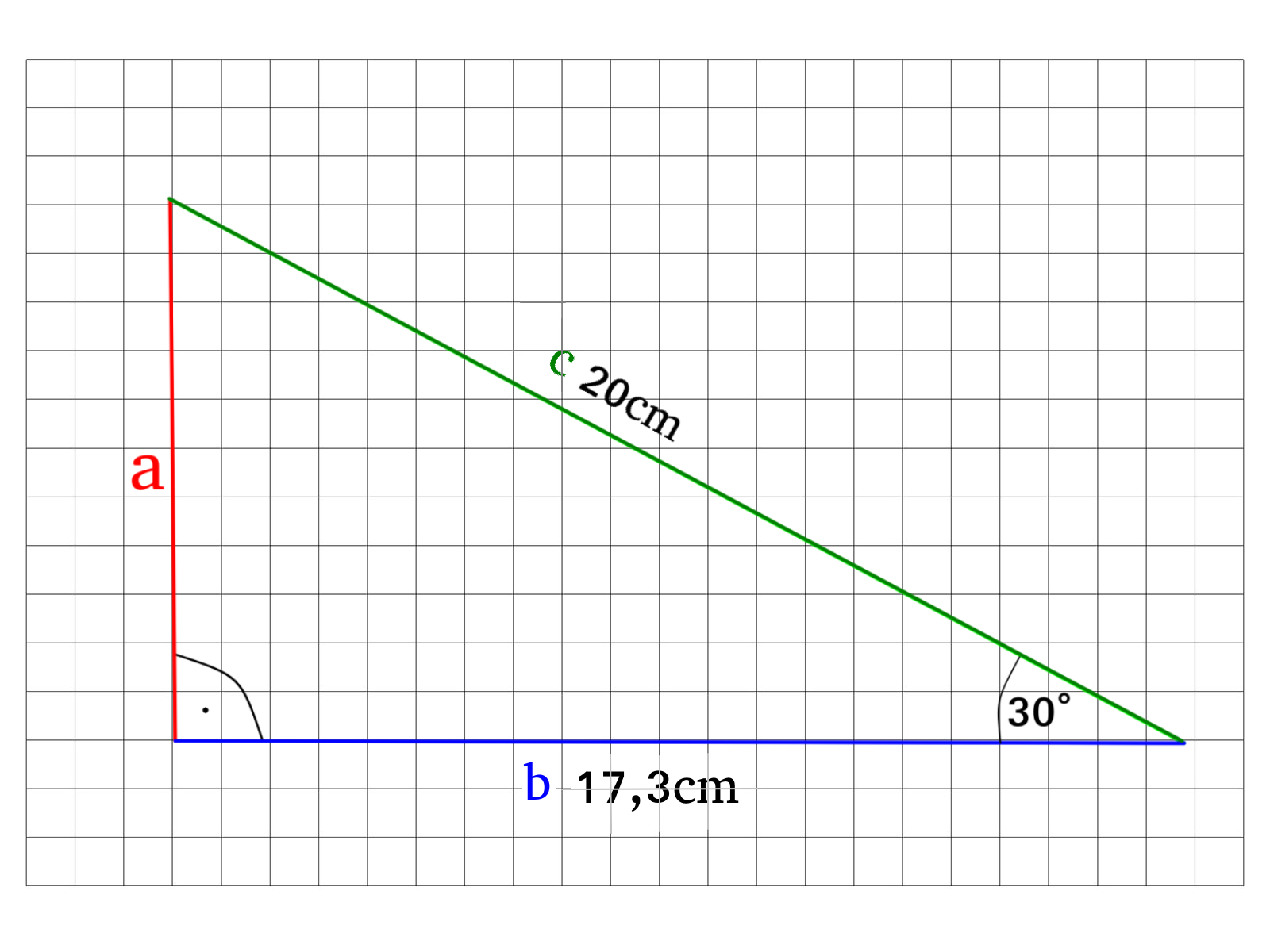
Um die Seitenlänge von \(a\) zu berechnen gibt es zwei Wege.
Weg 1:
Wir nutzen den Sinus um das Seitenverhältnis von \(a\) und \(c\) zu ermitteln:
\(sin(30°)=\)\(\frac{a}{c}=\frac{a}{20cm}\)
Diese Gleichung können wir wie jede andere Gleichung umstellen, das Umstellen von Gleichungen kannst du hier wiederholen.
\(sin(30°)=\)\(\frac{a}{20cm}\)\(\,\,\,\,\,\,|\cdot 20cm\)
\(sin(30°)\cdot 20cm=a\)
Wir wissen jetzt, dass
\(a=sin(30°)\cdot 20cm\)
wir könnnen im Tachenrechner nach dem \(sin\) suchen und dann den \(sin(30°)\) berechen. Dabei ist zu beachten, das der Taschenrechner auf deg bzw. DEG eingestellt ist. Den \(sin(30°)\) kannst du auch mit dem Rechner von Simplexy berechnen. Der Rechner ist auch in der lage die Gleichung \(sin(30°)=\)\(\frac{a}{20}\) für dich zu lösen. Hier kommst du zum Rechner. Der Rechner von Simplexy rechnet automatisch mit der Einstellung 'deg' darum braucht du dich also bei Simplexy nicht mehr zu kümmern.
Wir geben im Taschenrecher \(sin(30)\) ein und erhalten:
\(sin(30)=0,5\)
Damit bekommen wir die gesuchte Seitenlänge
\(a=sin(30°)\cdot 20cm=0,5\cdot 20cm=10cm\)
Die Seite \(a\) ist \(10cm\) lang.
Weg 2:
Wir nutzen den Tangens um das Seitenverhältnis von \(a\) und \(b\) zu ermitteln:
\(tan(30°)=\)\(\frac{a}{b}=\frac{a}{17,33cm}\)
\(tan(30°)=\)\(\frac{a}{17,33cm}\)\(\,\,\,\,\,\,|\cdot 17,33cm\)
\(tan(30°)\cdot 17,33cm=a\)
Du suchst im Taschenrechner nach dem tan knopf und berechnest \(tan(30)\). Nicht vergessen, der Taschenrechner muss auf deg bzw. DEG eingestellt sein.
\(tan(30)=0,577\)
Damit folgt:
\(tan(30°)\cdot 17,33cm=a\)
\(0,577\cdot 17,33cm=a\)
\(a=10,00cm\)
Die Länge von \(a\) beträgt \(10cm\).
Damit hast du zwei Methoden gesehen mit denen man auf die gewünschte Seitenlänge kommt, je nach Aufgabenstellung muss man verschiedene Winkelfunktionen benutzen um auf das Ziel zu kommen. Im folgenden werden noch weitere Aufgaben gelöst.
Umkehrfunktionen
Mit dem ersten Beispiel hast du gesehen das man mit Hilfe der Winkelfunktionen die fehlende Seitenlänge berechnen kann. Die Winkelfunktionen ermöglich aber auch den umgekehrten weg, sind die Seitenlängen bekannt, dann kann man die Winkeln zwischen ihnen berechnen, ohne je etwas messen zu müssen. Dazu benötigen wir die sogenannten Umkehrfunktionen von Sinus, Cosinus und Tangens.
Regel:
Die Winkelfunktionen Sinus, Kosinus und Tangens besitzen je eine Umkehrfunktion.
- Die Umkehrfunktion von \(sin\) wird \(sin^{-1}\), \(asin\) oder \(arcsin\) genannt.
- Die Umkehrfunktion von \(cos\) wird \(cos^{-1}\), \(acos\) oder \(arccos\) genannt.
- Die Umkehrfunktion von \(tan\) wird \(tan^{-1}\), \(arctan\) oder \(cot\) genannt.
Es kann sehr verwirrend sein, dass die Umkehrfunktionen so viele Namen besitzen. Der Name spielt aber keine Rolle für den Rechenweg. Auf deinem Taschenrechner kann also \(sin^{-1}\) oder \(asin\) stehten, sie sind beides das gleiche, nämlich die Umkehrfunktion von \(sin\). Wir werden hier für die Umkehrfunktion die schreibweise \(sin^{-1}\) verwenden, lass dich nicht davon verwirren falls dein Lehrer in der Schule eine andere schreibweise verwendet. Was genau ist die Umkehrfunktion für den \(sin\) ?
In Beispiel 1 hast du gesehen, dass \(sin(30)=0,5\) ist. Es gilt:
\(sin^{-1}(0,5)=30\)
Was genau ist hier passiert, schreiben wir das mal anderes auf:
\(sin^{-1}(0,5)=sin^{-1}(sin(30))=30\)
Man bezeichnet die Zahl die in den Klammern einer Funktion steht als Argument der Funktion, im Fall von \(sin(30)\) ist der Winkel \(30\) das Argument. Im Fall von \(sin^{-1}(0,5)\) ist das Argument \(0,5\). Es sieht so aus als könnte man mit der Funktion \(sin^{-1}\) herausfinden, was das Argument vom \(sin\) war.
Das Kann man auch allgemein schrieben als:
\(sin^{-1}(sin(\alpha))=\alpha\)
Das gleichen gilt natürlich auch für \(cos\) und \(tan\).
Regel:
- \(sin^{-1}(sin(\alpha))=\alpha\)
- \(cos^{-1}(cos(\alpha))=\alpha\)
- \(tan^{-1}(tan(\alpha))=\alpha\)
Wie wendet man die Umkehrfunktionen jetzt an ?
Beispiel 2:
Gegeben ist das folgende Dreieck, wie groß ist der Winkel \(\alpha\) ?
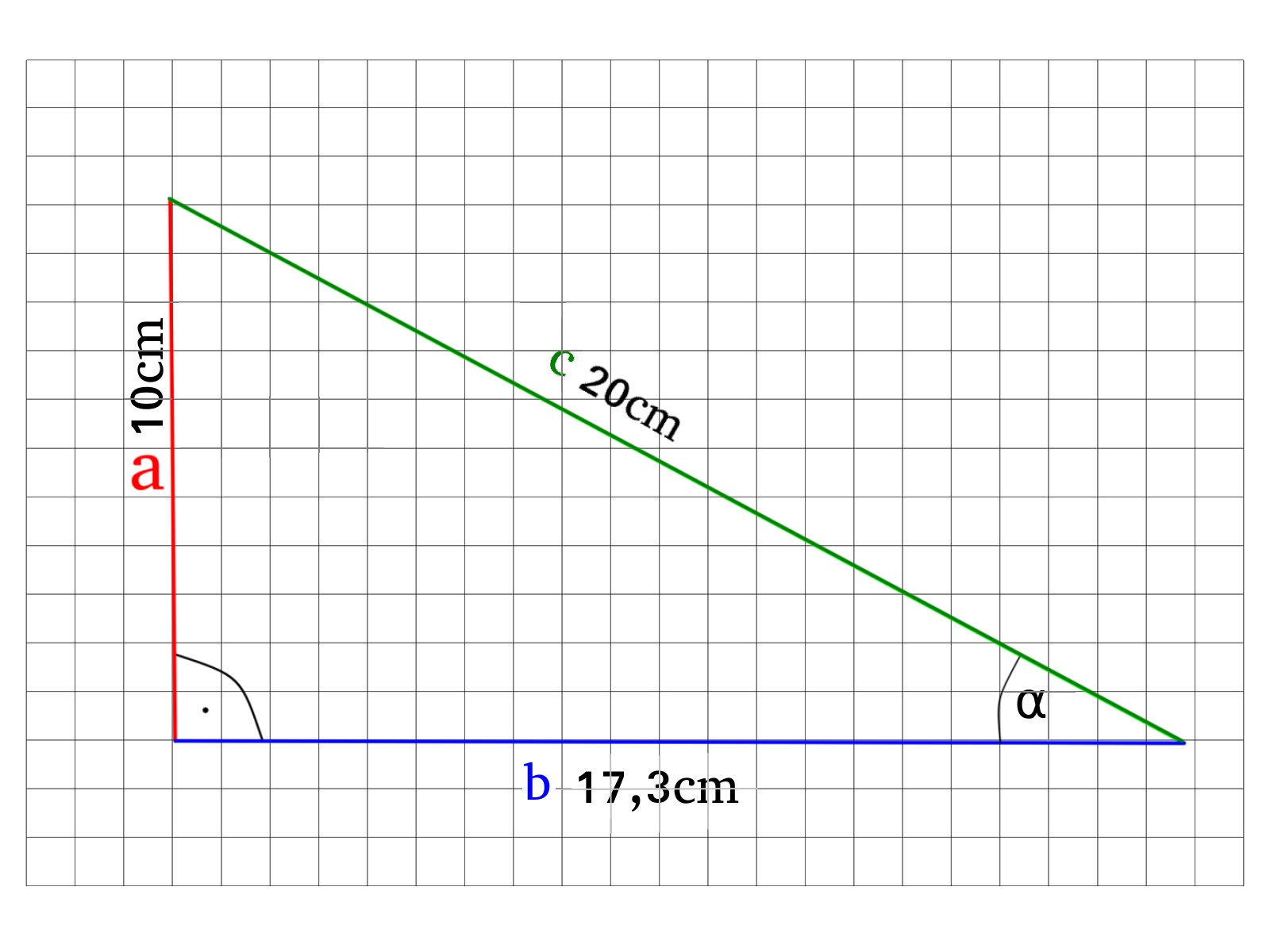
Bei so einer Aufgabe ist das Vorgehen sehr einfach, da uns alle drei Seiten gegeben sind können wir frei wählen, ob wir mit dem Sinus, Cosinus oder mit dem Tangens rechnen wollen. Wir entscheiden uns diesmal für den Cosinus.
Wir wissen bereits, dass folgendes gilt:
\(cos(\alpha)=\)\(\frac{Ankathete}{Hypotenus}=\frac{b}{c}\)
\(cos(\alpha)=\)\(\frac{17,3cm}{20cm}\)
\(cos(\alpha)=0,865\)
Um also auf den Winklen \(\alpha\) zu kommen müssen wir nur noch folgendes anwenden:
\(cos^{-1}(cos(\alpha))=\alpha\)
\(cos^{-1}(0,865)\approx 30°\)
Der Winkel \(\alpha\) ist ca. \(30°\) groß.
Aufgaben
Das rechnen mit den Winkelfunktionen benötigt Übung, du kannst versuchen die nächsten zwei Aufgaben zu lösen. Solltest du Hilfe brauchen kannst du immer den Rechner von Simplexy benutzen.
Hier kommst du zum online Rechner.
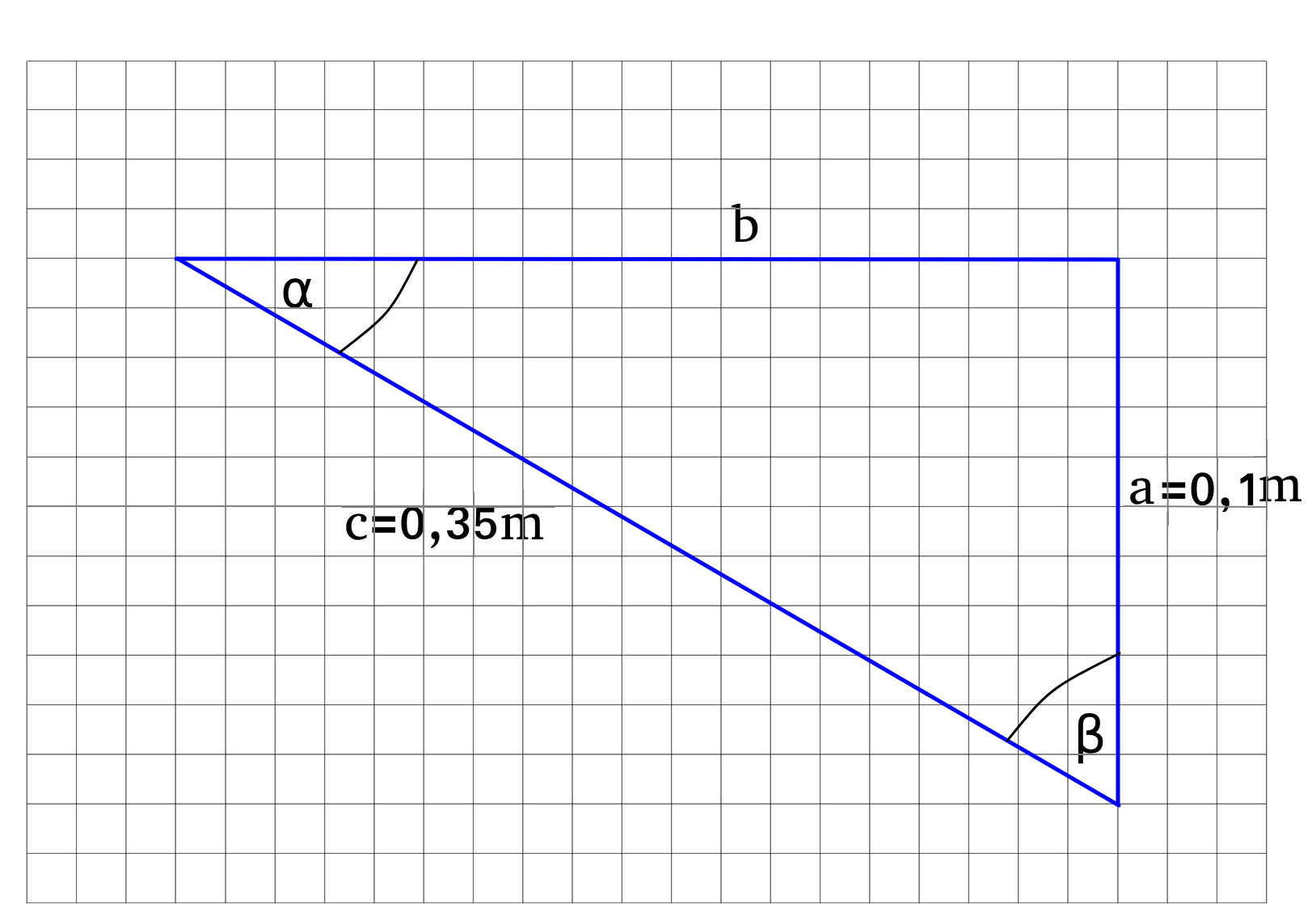
Aufgabe 1
Gegeben ist das folgende Dreieck, berechne alle fehlenden Seitenlängen und Winkeln
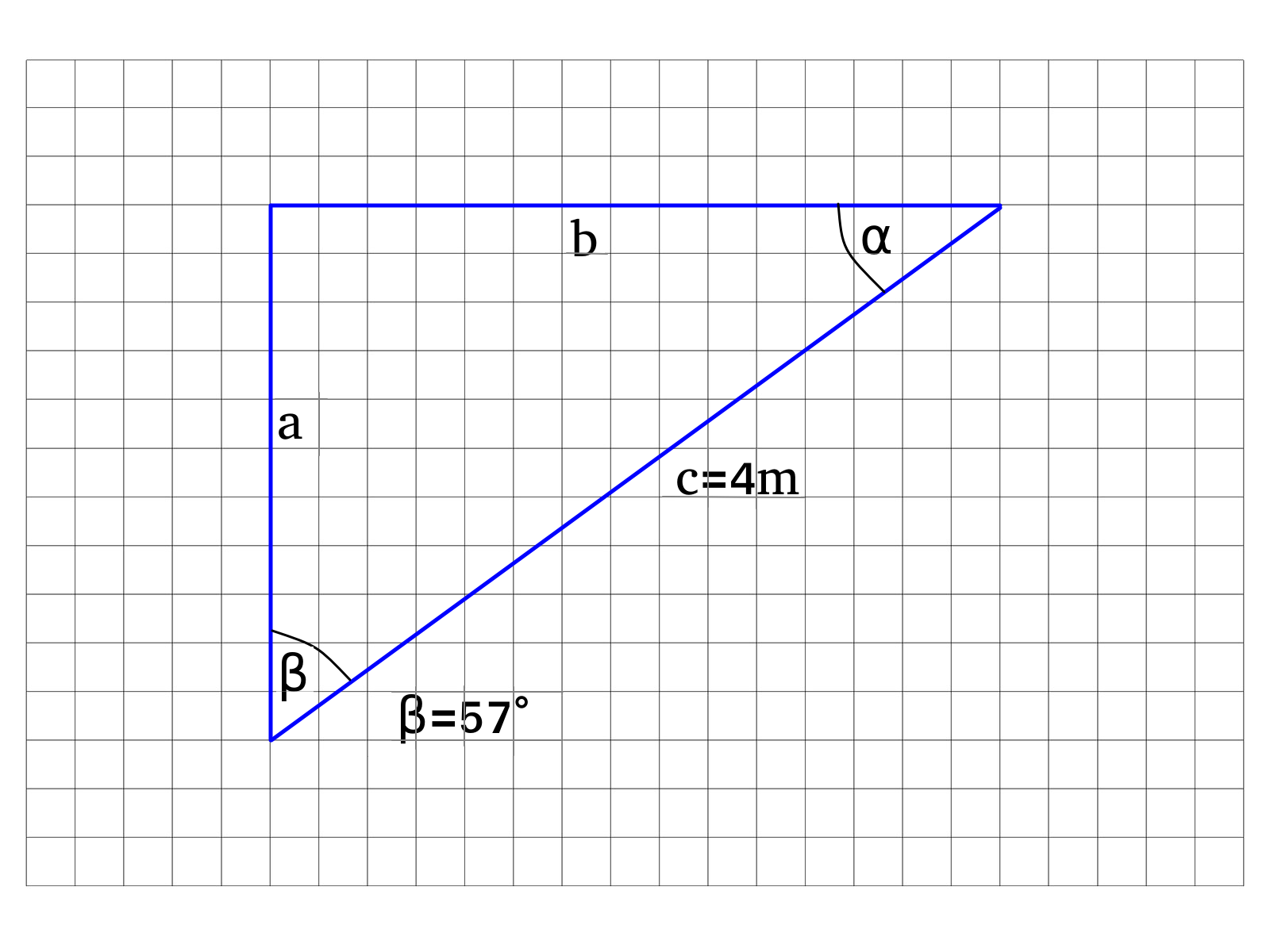
Aufgabe 2
Gegeben ist das folgende Dreieck, berechne alle fehlenden Seitenlängen und Winkeln