Parallelschaltung - Verzweigter Stromkreis
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Formeln im Überblick
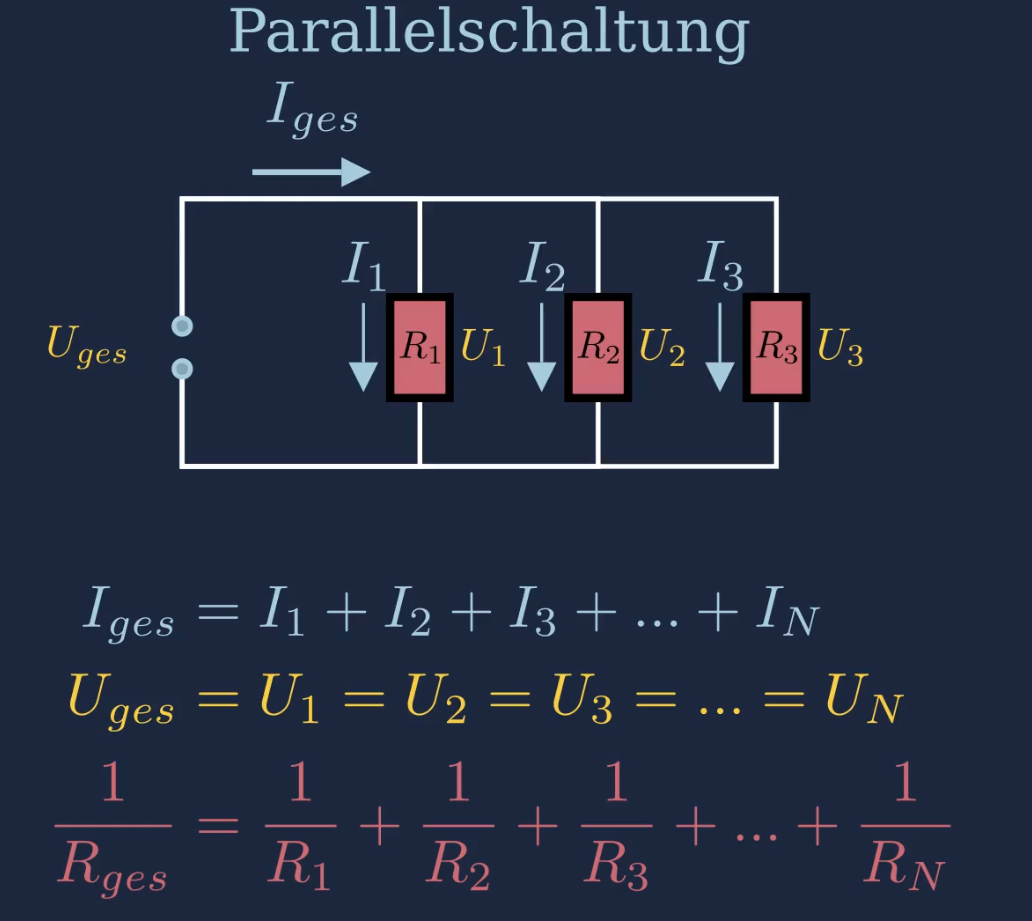
Parallelschaltung von Widerständen
\(\frac{1}{R_{ges}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+...\)
Parallelschaltung von 2 Widerständen
\(R_{ges}\)\(=\frac{R_1\cdot R_2}{R_1+R_2}\)
Verhalten des Stroms in einer Parallelschaltung
\(I_{ges}=I_1+I_2+I_3+...\)
Verhalten der Spannung in einer Parallelschaltung
\(U_{ges}=U_1=U_2=U_3=...\)
Parallelschaltung Erklärt
Stromkreise bestehen oftmals aus mehreren elektrischen Bauteilen. Sind beispielsweise mehrere Widerstände in einer Schaltung vorhanden, dann hängt der Gesamtwiderstand davon ab ob sie in Reihe oder Parallel geschalten sind. Die frage ist nun, wie man bei einer Reihenschaltung und einer Parallelschaltung das Ohmsche Gesetz sinnvoll anwenden kann. In diesem Artikel soll es zunächst nur um die Parallelschaltung gehen.
Zusatz Information
Solltest du die Begriffe Stromstärke, Spannung und Widerstand nochmal wiederholen wollen, dann kannst du das hier machen.
Für eine Wiederholung des Ohmschen Gesetzes, kannst du diesen Artikel durchlesen.
Parallelschaltung Wiederstand berechnen
In dem letzten Artikel über das Ohmsche Gesetz haben wir uns bereits mit einem Stromkreis beschäftigt, in dem mehrere Widerstände auftauchen. Sollest du in einem Schaltkreis Widerstände finden, in denen zwei oder mehr Widerstände parallel angeordnet sind, dann spricht man von einer Parallelschaltung. Ein Beispiel für drei parallele Widerstände findest du im unteren Bild.
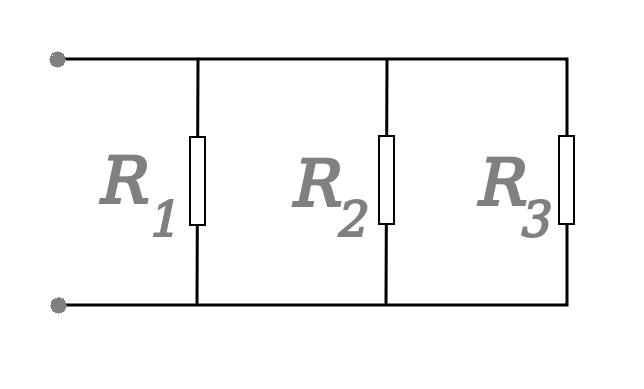
In den meisten Fällen werden die Widerstände durch nummeriert, wie auch hier in diesem Beispiel. Befinden sich die Widerstände in einer Parallelschaltung, so ist der Kehrwert des Gesamtwiderstand genau so groß wie du Summe aus den Kehrwerten der Einzelwiderstände. Dazu werden diese Kehrwerte folgendermaßen addiert:
Parallelschaltung von Widerständen
\(\frac{1}{R_{ges}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+...\)
Parallelschaltung von 2 Widerständen
\(R_{ges}\)\(=\frac{R_1\cdot R_2}{R_1+R_2}\)
Bei einer Parallelschaltung von Widerständen, besteht der Kehrwert des Gesamtwiderstand aus der Summe der Kehrwerte der Einzelwiderstände.
Hinweis
Bei einer Parallelschaltung ist der Gesamtwiderstand kleiner als der kleinste Einzelwiderstand. Besteht die Parallelschaltung aus zwei identischen Widerständen, so entspricht der Gesamtwiderstand der Hälfte eines Teilwiderstandes.
Parallelschaltung Stromstärke und Spannung berechnen
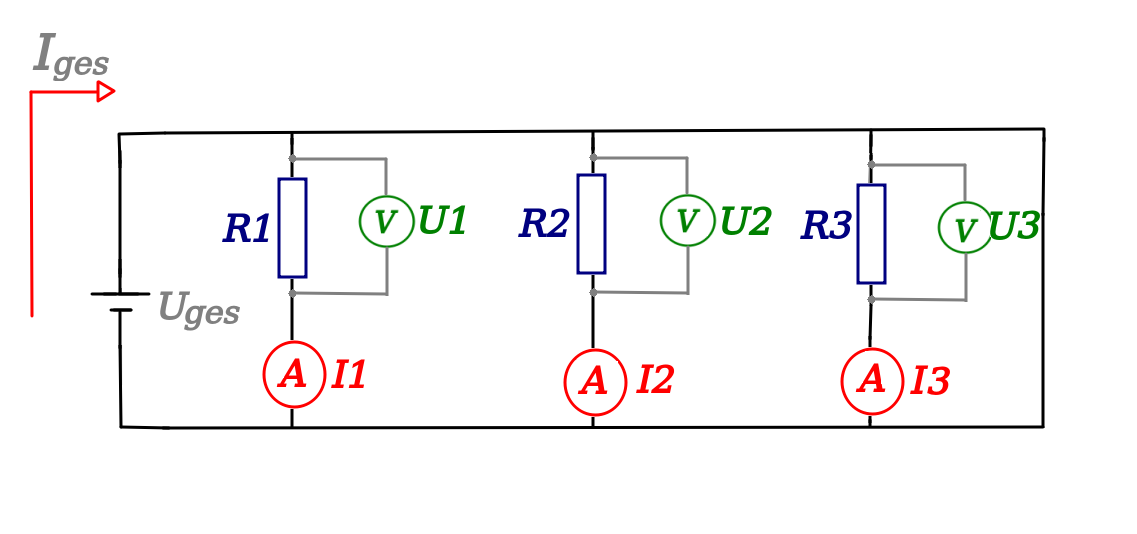
Wie verhält sich die Stromstärke und die Spannung bei einer Parallelschaltung ?
Verhalten des Stroms in einer Parallelschaltung
\(I_{ges}=I_1+I_2+I_3+...\)
Der Strom in einer Parallelschaltung teilt sich auf alle Widerstände auf.
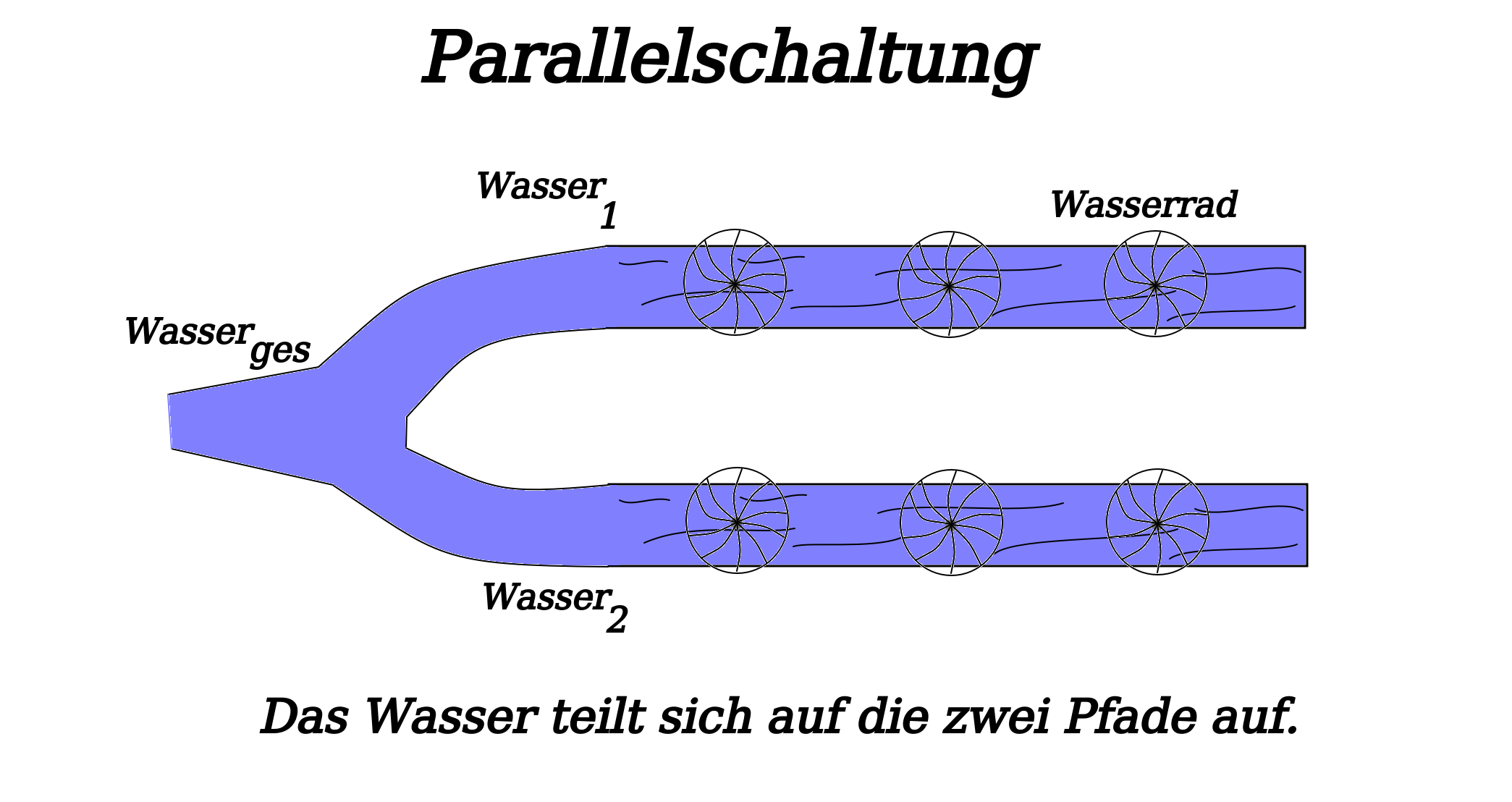
Handelt es sich um eine Parallelschaltung, dann teilt sich der Gesamtstrom auf alle elektrische Bauteile auf. Im Artikel Strom, Spannung und Widerstand haben wir bereits die Analogie zwischen Strom und Wasser benutzt. Bei einer Parallelschaltung gibt es für das Wasser mehrere Verzweigung durch die es fließen kann (durch alle Bauteile). Der Strom bzw. das Wasser wird sich auf alle möglichen Fade aufteilen.
Verhalten der Spannung in einer Parallelschaltung
\(U_{ges}=U_1=U_2=U_3=...\)
Bei einer Parallelschaltung haben alle Bauteile die gleiche Spannung nämlich die Gesamtspannung \(U_{ges}\).
Dadurch dass die Spannungen in einer Parallelschaltung überall gleich sind, verursachen die verschiedenen Widerstände unterschiedliche Teilströme. Dabei verhalten sich die Ströme umgekehrt zu ihren Widerständen. Durch einen hohen Widerstand fließt ein kleiner Strom während durch einen kleinen Widerstand ein hohe Strom fließt.
Die Ströme \(I_1\) und \(I_2\) verhalten sich umgekehrt zu ihren Widerständen.
\(\frac{R_1}{R_2}=\frac{I_2}{I_1}\)
Parallelschaltung Beispiel
Parallelschaltung Gesamtwiderstand berechnen
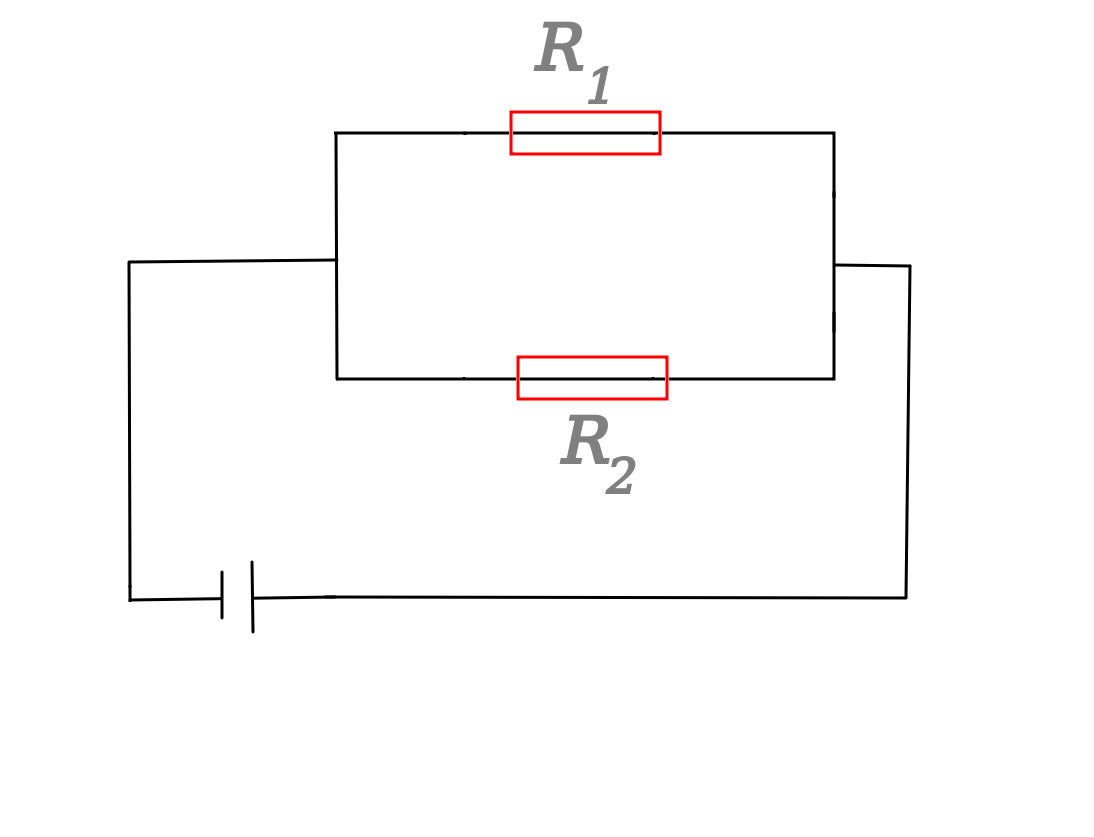
Betrachten wir den folgenden Stromkreis.
Die Widerstände haben folgende Werte: \(R_1=40\Omega\), \(R_2=10\Omega\).
Die Angelegte Spannung beträgt \(U=230V\).
Wie groß ist der Gesamtwiderstand des Stromkreises ?
Durch welchen Widerstand fließt der höhere Strom und um wie viel höher ist der Strom gegenüber dem anderen Widerstand ?
Lösung
Zunächst berechnen wir den Gesamtwiderstand berechen:
\(R_{ges}\)\(=\frac{40\Omega\cdot 10\Omega}{40\Omega+10\Omega}\)
\(R_{ges}\)\(=\frac{400\Omega^2}{50\Omega}\)
\(R_{ges}=8\Omega\)
Der Gesamtwiderstand des Stromkreises beträgt 8 Ohm.
Da sich die Ströme umgekehrt zu den Widerständen verhalten, fließt durch den kleineren Widerstand \(R_2\) einen größern Strom als durch den Widerstand \(R_1\). Um den Strom zu berechnen der durch die Widerstände fließt, verwenden wir folgende Formel:
\(\frac{R_1}{R_2}=\frac{I_2}{I_1}\)
\(\frac{40\Omega}{10\Omega}\)\(=4\)
\(\implies \frac{I_2}{I_1}\)\(=4\)
\(\frac{I_2}{I_1}\)\(=4\,\,\,\,\,\,|\cdot I_1\)
\(I_2=4\cdot I_1\)
Durch den Widerstand \(R_2\) fließt vier mal so viel strom wie durch den Widerstand \(R_1\).
Möchte man wissen wie viel strom genau durch den Wiederstand \(R_2\) fließt, so kann man das Ohmsche Gesetz verwenden. Dabei muss man beachten, dass beide Widerstände aufgrund der Parallelschaltung die gleiche Spannung besitzen.
\(I_2\)\(=\frac{U}{R_2}\)
\(I_2\)\(=\frac{230V}{10\Omega}\)
\(I_2=23\)\(\frac{V}{\Omega}\)
\(I_2\)\(=23 A\)
Durch den Widerstand \(R_2\) fließt ein Strom von \(23\) Ampere.
Da wir schon berechnent haben, dass durch \(R_2\) vier mal soviel Strom fließt wie durch \(R_1\) wissen wir, dass
\(I_1=\)\(\frac{I_2}{4}\)
\(I_1=\)\(\frac{23A}{4}\)
\(I_1=5,75A\)
Durch den Widerstand \(R_1\) fließt ein Strom von \(5,75\) Ampere.
