Ableitung von Brüchen
Ableitungsrechner
Der Ableitungsrechner von Simplexy kann beliebige Funktionen für dich Ableiten und noch viel mehr. Um zum Beispiel die Funktion \(f(x)=x^2\) abzuleiten, geh auf den knopf \(\frac{df}{dx}\) und gib \(x^2\) ein. Dann kannst du auf Lösen drücken und du erhälts die Ableitung deiner Funktion. Teste den Rechner mit Rechenweg aus.
Ein Bruch umschreiben
Die Ableitung von Brüchen haben wir bereits im letzten Beitrag zur Quotientenregel behandelt. Manche Brüche lassen sich jedoch auch auf eine andere, oftmals einfachere Art ableiten. In dem unteren Video wird eine alternative Methode zum Ableiten von Brüchen erklärt.
Bruch umschreiben
Einige Brüche können in eine Potenzfunktion umgeschrieben werden.
\(\begin{aligned} \frac{1}{x}&=x^{-1}\\ \\ \frac{1}{x^2}&=x^{-2}\\ \\ \frac{1}{x^3}&=x^{-3}\\ \end{aligned}\)
Dabei handelt es sich lediglich um eine neue Schreibweise für den Bruch. Diese neue Schreibweise kann man genau so verinnerlichen wie die Schreibweise:
\(\begin{aligned} x\cdot x=x^2 \end{aligned}\)
Es handelt sich dabei ebenfalls nur um eine mathematische Notation die oftmals das Rechnen erleichtert. Das Umschreiben eines Bruchs in eine Potenzfunktion erleichtert die Berechnung der Ableitung.
Regel:
Umschreiben von Brüchen
Einen Bruch der Form
\(\begin{aligned} \frac{1}{x} \end{aligned}\)
kann in eine Potenzfunktion mit einem negativen Exponenten umgeschrieben werden. Dabei hängt der Grand \(\textcolor{blue}{n}\) der Potenz vom Grand \(\textcolor{blue}{n}\) des Nenners ab:
\(\begin{aligned} \frac{1}{x^\textcolor{blue}{1}}&=x^{\textcolor{blue}{-1}}\\ \\ \frac{1}{x^\textcolor{blue}{2}}&=x^{\textcolor{blue}{-2}}\\ \\ \frac{1}{x^\textcolor{blue}{3}}&=x^{\textcolor{blue}{-3}}\\ &...\\ \frac{1}{x^\textcolor{blue}{n}}&=x^{\textcolor{blue}{-n}}\\ \end{aligned}\)
Durch die Umschreibung des Bruchs in eine Potenzfunktion, kann die Ableitung mittels Potenzregel berechnet werden.
Befinden sich im Zähler und im Nenner weitere Zahlen, so müssen diese wie folgt berücksichtigt werden
\(\begin{aligned} \frac{\textcolor{green}{1}}{x^\textcolor{blue}{1}}&=\textcolor{green}{1}x^{\textcolor{blue}{-1}}\\ \\ \frac{\textcolor{green}{1}}{\textcolor{red}{2}x^\textcolor{blue}{1}}&=\frac{\textcolor{green}{1}}{\textcolor{red}{2}}x^{\textcolor{blue}{-1}}=\textcolor{green}{1}(\textcolor{red}{2}x)^{\textcolor{blue}{-1}}\\ \\ \frac{\textcolor{green}{3}}{\textcolor{red}{5}x^\textcolor{blue}{2}}&=\frac{\textcolor{green}{3}}{\textcolor{red}{5}}x^{\textcolor{blue}{-2}}=\textcolor{green}{3}(\textcolor{red}{5}x)^{\textcolor{blue}{-2}}\\ \\ \frac{\textcolor{green}{8}}{x^\textcolor{blue}{3}}&=\textcolor{green}{8}x^{\textcolor{blue}{-3}}\\ \\ \frac{\textcolor{green}{1}}{\textcolor{red}{7}x^\textcolor{blue}{5}}&=\frac{\textcolor{green}{1}}{\textcolor{red}{7}}x^{\textcolor{blue}{-5}}=(\textcolor{red}{7}x)^{\textcolor{blue}{-5}}\\ \\ \end{aligned}\)
Bruch ableiten
Nachdem man einen Bruch in eine Potenzfunktion umgeschrieben hat, kann die Ableitung mittels Potenzregel berechnet werden.
Beispiel 1
Berechne die Ableitung der Funktion
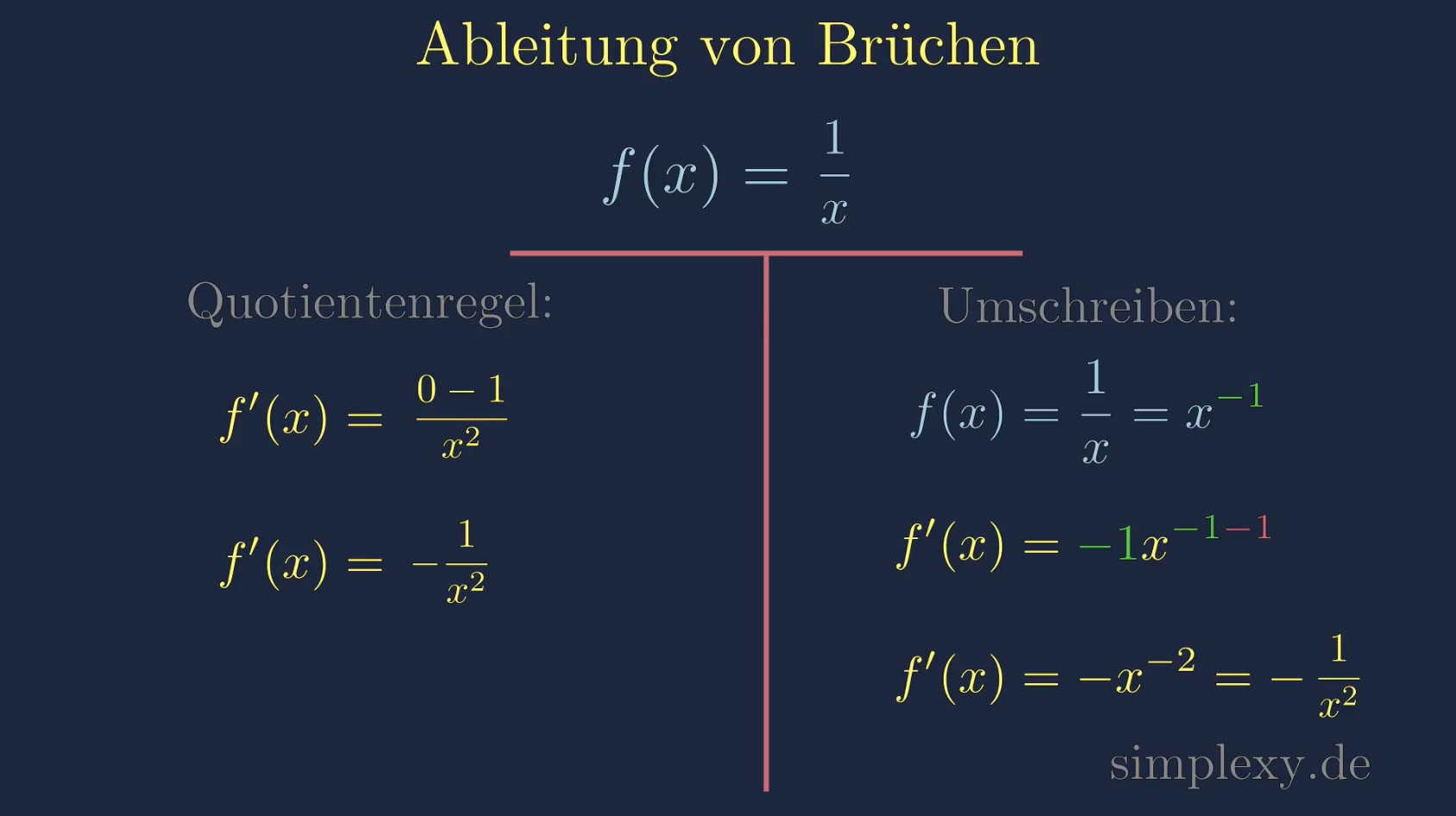
\(\begin{aligned} f(x)=\frac{1}{x} \end{aligned}\)
Lösung:
Zunächst scheiben wir den Bruch in eine Potenzfunktion um:
\(\begin{aligned} f(x)&=\frac{1}{x}=x^{\textcolor{blue}{-1}}\\ \end{aligned}\)
Nun können wir die Potenzregel anwenden, dazu bringen wir den Exponenten \(\textcolor{blue}{-1}\) nach vorne und ziehen dann eine \(\textcolor{red}{1}\) ab.
\(\begin{aligned} f'(x)&=\textcolor{blue}{-1}x^{\textcolor{blue}{-1}-\textcolor{red}{1}}\\ &=-1x^{-2} \end{aligned}\)
Die Ableitung können wir wieder in einen Bruch umschreiben:
\(\begin{aligned} f'(x)=-1x^{-2}=-\frac{1}{x^2} \end{aligned}\)
Bruch Ableiten
Die Ableitung von
\(\begin{aligned} f(x)=\frac{1}{x^\textcolor{blue}{n}} \end{aligned}\)
lautet:
\(\begin{aligned} f'(x)=\textcolor{blue}{-n}x^{\textcolor{blue}{-n}-\textcolor{red}{1}}=\textcolor{blue}{-}\frac{\textcolor{blue}{n}}{x^{\textcolor{blue}{n}+\textcolor{red}{1}}} \end{aligned}\)
Beispiel 2
Bestimme die Ableitung der Funktion
\(\begin{aligned} f(x)=\frac{1}{x^2} \end{aligned}\)
Lösung:
Damit wir die Ableitung nicht über die Q uotientenregel berechnen müssen, werden wir den Bruch in eine Potenzfunktion umschreiben:
\(\begin{aligned} f(x)&=\frac{1}{x^2}=x^{\textcolor{blue}{-2}}\\ \end{aligned}\)
Nun können wir die Potenzregel anwenden, dazu bringen wir den Exponenten \(\textcolor{blue}{-2}\) nach vorne und ziehen dann eine \(\textcolor{red}{1}\) ab.
\(\begin{aligned} f'(x)&=\textcolor{blue}{-2}x^{\textcolor{blue}{-2}-\textcolor{red}{1}}\\ &=-2x^{-3} \end{aligned}\)
Die Ableitung können wir wieder in einen Bruch umschrieben:
\(\begin{aligned} f'(x)=-2x^{-3}=-\frac{2}{x^3} \end{aligned}\)
Beispiel 3
Wie lautet die Ableitung der Funktion
\(\begin{aligned} f(x)=\frac{2}{x^3} \end{aligned}\)
Lösung:
Wir schreiben den Bruch wieder in eine Potenzfunktion um:
\(\begin{aligned} f(x)&=\frac{\textcolor{green}{2}}{x^\textcolor{blue}{3}}=\textcolor{green}{2}x^{\textcolor{blue}{-3}}\\ \end{aligned}\)
Nun können wir die Potenzregel anwenden, dazu bringen wir den Exponenten \(\textcolor{blue}{-3}\) nach vorne und ziehen dann eine \(\textcolor{red}{1}\) ab.
\(\begin{aligned} f'(x)&=\textcolor{green}{2}\cdot(\textcolor{blue}{-3})x^{\textcolor{blue}{-3}-\textcolor{red}{1}}\\ &=-6x^{-4} \end{aligned}\)
Die Ableitung können wir wieder in einen Bruch umschrieben:
\(\begin{aligned} f'(x)=-6x^{-4}=-\frac{6}{x^4} \end{aligned}\)
Beispiel 4
Berechne die Ableitung der Funktion
\(\begin{aligned} f(x)=\frac{1}{2x^3} \end{aligned}\)
Lösung:
Zunächst schreiben wir den Bruch in eine Potenzfunktion um:
\(\begin{aligned} f(x)&=\frac{1}{\textcolor{green}{2}x^\textcolor{blue}{3}}=\frac{1}{\textcolor{green}{2}}x^{\textcolor{blue}{-3}}\\ \end{aligned}\)
Nun können wir die Potenzregel anwenden, dazu bringen wir den Exponenten \(\textcolor{blue}{-3}\) nach vorne und ziehen dann eine \(\textcolor{red}{1}\) ab.
\(\begin{aligned} f'(x)&=\frac{1}{\textcolor{green}{2}}\cdot(\textcolor{blue}{-3})x^{\textcolor{blue}{-3}-\textcolor{red}{1}}\\ &=-\frac{3}{2}x^{-4} \end{aligned}\)
Die Ableitung können wir wieder in einen Bruch umschrieben:
\(\begin{aligned} f'(x)=-\frac{3}{2}x^{-4}=-\frac{3}{2x^{4}} \end{aligned}\)
