Kurvendiskussion
Kurvendiskussion Rechner
Der Online Rechner von Simplexy kann dir bei der Kurvendiskussion sehr helfen. Mit dem Kurvendiskussion Rechner kannst du die Extrempunke, Wendepunkte und viel mehr berechnen.
Grundlagen der Kurvendiskussion
In dem folgenden Video wird die Kurvendiskussion eingeführt. Wenn du mehr über die Berechnung von Extremstellen (Hochpunkt und Tiefpunkt) lernen möchtest, dann kannst du dir gerne die restlichen Videos in der Playlist ansehen.
Was ist eine Kurvendiskussion?
Mit einer Kurvendiskussion kannst du viele geometrische eigenschaften einer Funktion untersuchen:
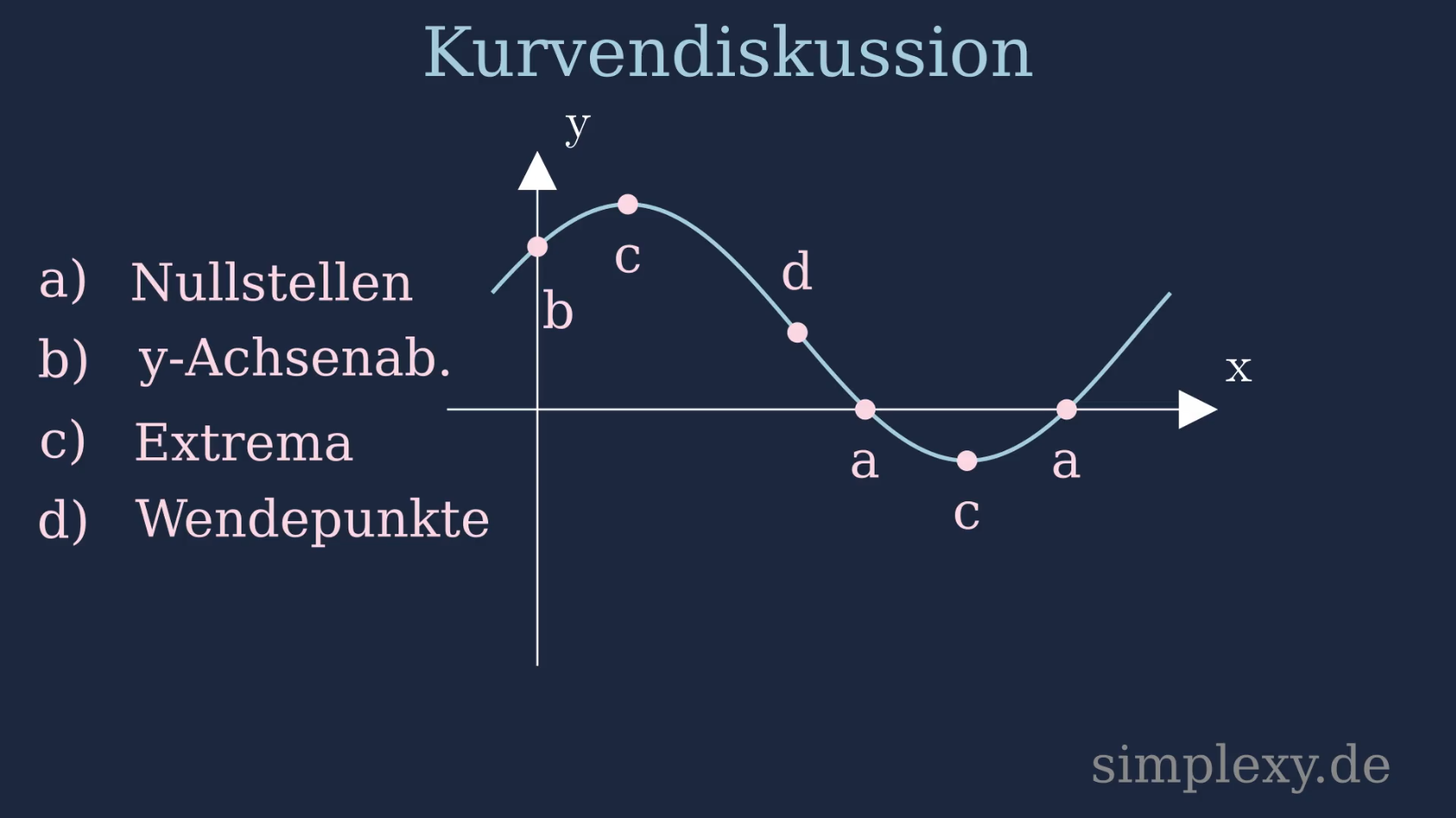
- a) Nullstellen
- b) Schnittpunkt mit der \(y\)-Achse
- c) Extrempunkte: Hochpunkte und Tiefpunkte
- d) Wendepunkte
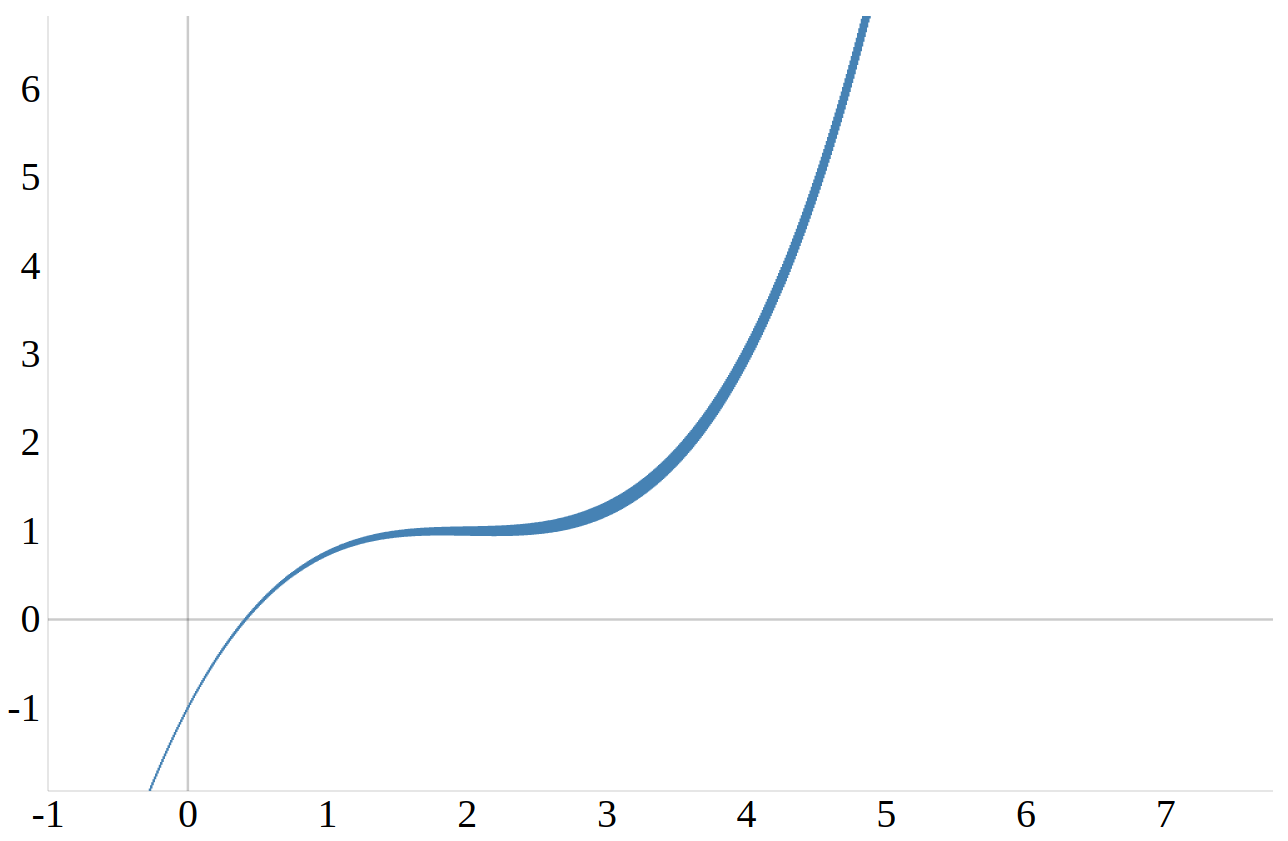
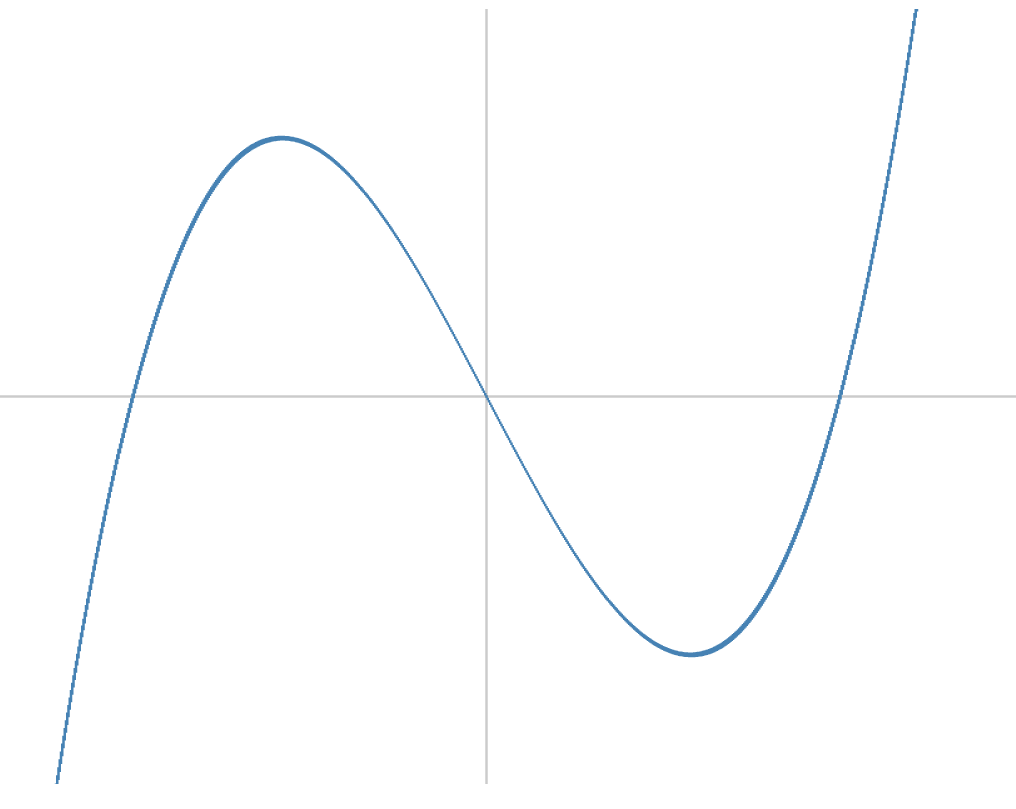
Wie du in dem Bild hier oben siehst, kann eine Funktion viele signifikante Stellen besitzen. Eine Funktion kann zum Beispiel Extrempunkte besitzen, dass sind die Hochpunkte und Tiefpunkte einer Funktion. Um die Koordinaten dieser Extrempunkte zu ermitteln muss man eine Kurvendiskussion durchführen. Über die Ableitungen der betrachten Funktion erhält man Informationen über die Position der Extrempunkte. Im Folgenden wirst du sehen wie genau das gemacht wird.
Extrempunkte berechnen - Kurvendiskussion
Die Berechnung von Extrempunkten ist in dem folgenden Video exemplarisch vorgerechnet.
In den nächsten Videos wird auf die notwendige und hinreichende Bedingung für die Existenz von Extremstellen eingegangen.
1. Notwendige Bedingung:
\(f'(x_E)=0\)
\(\implies\)
potentielle Extremstelle bei \(x_E\)
Ist die erste Ableitung einer Funktion an der Stelle \(x_E\) gleich Null, dann wissen wir, dass sich dort ein potentieller Extrempunkt befindet.
Eine Funktion kann mehrere potentielle Extremstellen besitzen.
Nicht jede potentielle Extremstelle ist auch ein Hochpunkt oder ein Tiefpunkt. Wenn man den Graphen einer Funktion nicht vor Auge hat, dann kann man nicht sofort wissen ob eine potentielle Extremstelle auch wirklich eine Extremstelle ist. Man muss noch die hinreichende Bedingung betrachten.
2. Hinreichende Bedingung:
\(f'(x_E)=0\) und \(f''(x_E)\ne 0\)
\(\implies\)
Extremstelle bei \(x_E\).
Ist die erste Ableitung einer Funktion an einer potentiellen Extremstelle \(x_E\) null und die zweite Ableitung der Funktion an dieser potentiellen Extremstelle ungleich Null, dann wissen wir, dass sich dort ein Extrempunkt befindet.
Für die zweite Ableitung an einer potentiellen Extremstelle \(f''(x_E)\) kann folgendes rauskommen:
- \(f''(x_E)\lt 0\,\,\implies\,\,x_E\) ist ein Hochpunkt
- \(f''(x_E)\gt 0\,\,\implies\,\,x_E\) ist ein Tiefpunkt
- \(f''(x_E)= 0\,\,\implies\,\,x_E\) ist kein Extrempunkt
Hinreichende und Notwendige Bedingung für Extremstellen
1. Notwendige Bedingung:
\(f'(x_E)=0\)
\(\implies\) potentielle Extremstelle
2. Hinreichende Bedingung:
\(f'(x_E)=0\)
und
\(f''(x_E)\ne 0\)
\(\implies\) Extremstelle
Achtung !
Eine Funktion kann mehrere Hochpunkte oder Tiefpunkte besitzen, man unterscheidet dann zwischen lokalen und globalen (oder absoluten) Extremstellen.
Mit dem Kurvendiskussion Rechner von Simplexy kannst du die Extrempunkte einer Funktion berechnen und den dazugehörigen Rechenweg ansehen.
Extrempunkte berechnen Beispiel
Untersuche die Funktion
\(f(x)=\frac{1}{12}x^3+x^2\)
auf Extremstellen.
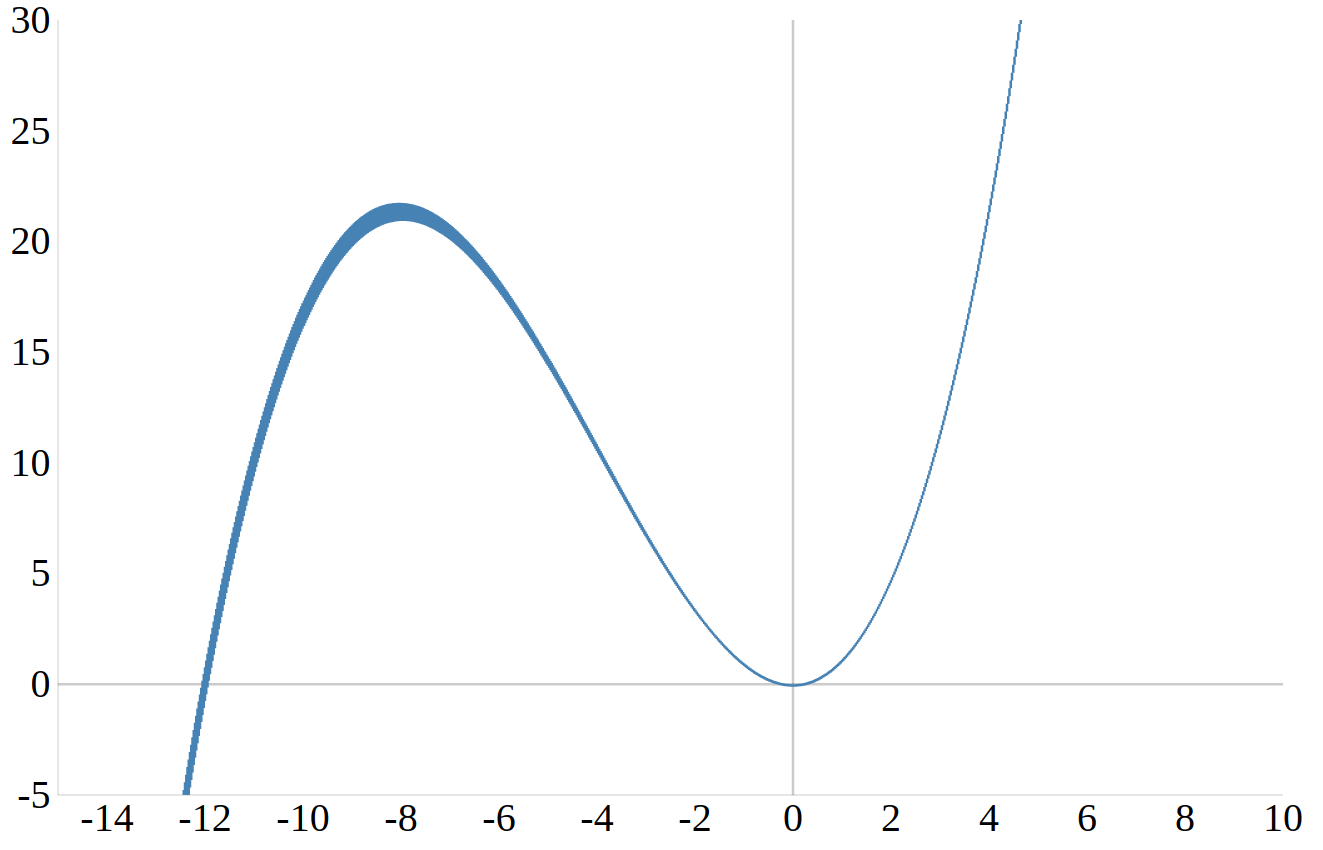
Schritt 1 - Bilde die erste Ableitung und setze sie gleich Null:
\(f'(x)=\frac{1}{4}x^2+2x=0\)
Löst man diese Gleichung mit der pq-Formel, dann erhält man als potentielle Extremwerte
\(x_1=0\) und \(x_2=-8\)
Schritt 2 - Berechne die zweite Ableitung und setze \(x_1\) und \(x_2\) ein:
\(f''(x)=\frac{1}{2}x+2\)
- \(x_1\) einsetzen:
- \(x_2\) einsetzen:
\(f''(x_1)=\frac{1}{2}\cdot 0 +2\gt 0\)
\(\implies\)
\(x_1\) ist ein Minimum
\(f''(x_2)=\frac{1}{2}\cdot (-8) +2\lt 0\)
\(\implies\)
\(x_2\) ist ein Maximum
Schritt 3 - Die Extrempunkte in die Ausgangsfunktion einsetzten:
\(y_1=f(x_1)=0\)
\(y_2=f(x_2)=\frac{64}{3}\)
Die Funktion besitzt bei
\((0|0)\) ein Minimum
und bei
\((-8|\frac{64}{3})\) ein Maximum.
Mit dem Rechner von Simplexy kannst du Ableitungen berechnen und diese Ableitung auch Nullsetzen. So kannst du immer überprüfen ob du die richtigen Hochpunkte und Tiefpunkte berechnet hast.
Lokale und Globale Extremstellen
Extrempunkte werden in lokale und globale Extrempunkte unterschieden. Ein Extrempunkt ist ein globaler Extrempunkt, wenn er der "höchste" bzw. der "niedrigste" Punkt der Funktion ist. Ein lokaler Extrempunkt ist lediglich in einer bestimmten Umgebung der "höchste" bzw. niedrigste Punkt der Funktion.

Ein globaler Extrempunkt ist auch immer ein lokaler Extrempunkt.
Mehr zum Thema lokaler und globaler Tiefpunkte bzw. Hochpunkte erfährt man im folgenden Video:
Du möchtest gerne die Hochpunkte und tiefpunkte einer Funktion berechnen, dann kannst du dies mit dem Kurvendiskussion Rechner machen.
Wendepunkte berechnen
Ein Wendepunkt ist ein Punkt auf einer Funktion, indem die Funktion seine Krümmung ändert.
1. Notwendige Bedingung:
\(f''(x_W)=0\)
\(\implies\)
potentielle Wendestelle bei \(x_W\)
2. Hinreichende Bedingung:
\(f''(x_W)=0\) und \(f'''(x_W)\ne 0\)
- \(f'''(x_W)\lt 0\)
- \(f'''(x_W)\gt 0\)
\(\implies\) Links-Rechts-Wendestelle
\(\implies\) Rechts-Links-Wendestelle
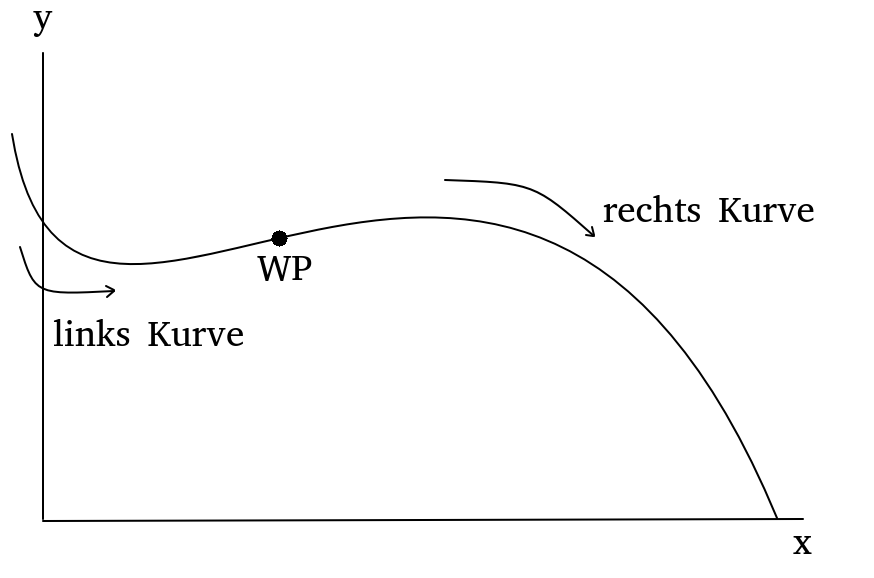
Bei einem Wendepunkt handelt es sich um einen Punkt, bei dem der Funktionsgraph seine Krümmung ändert. Dabei geht der Graph entweder von einer Links- in eine Rechtskurve oder umgekehrt. Meistens ist der Wendepunkt gesucht wenn in der Aufgabenstellung nach der stärksten Zunahme bzw. Abnahme gefragt wird.
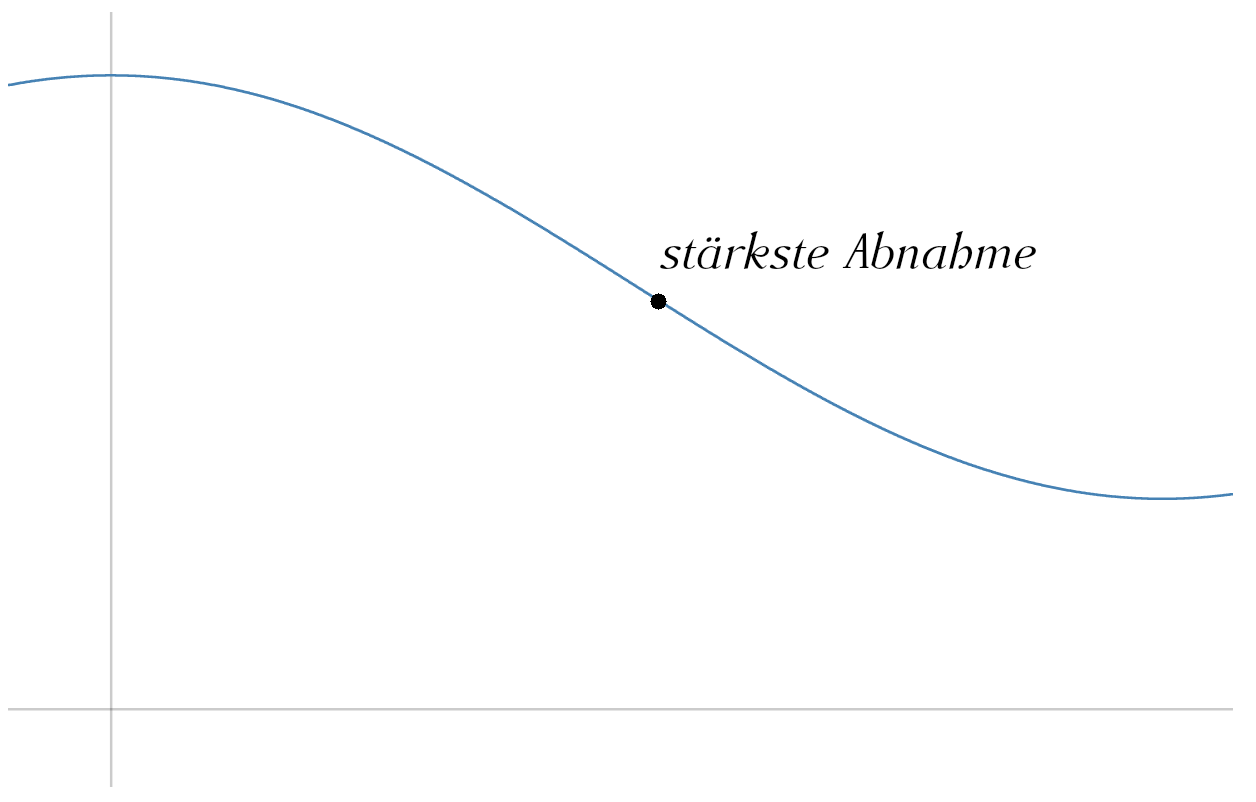
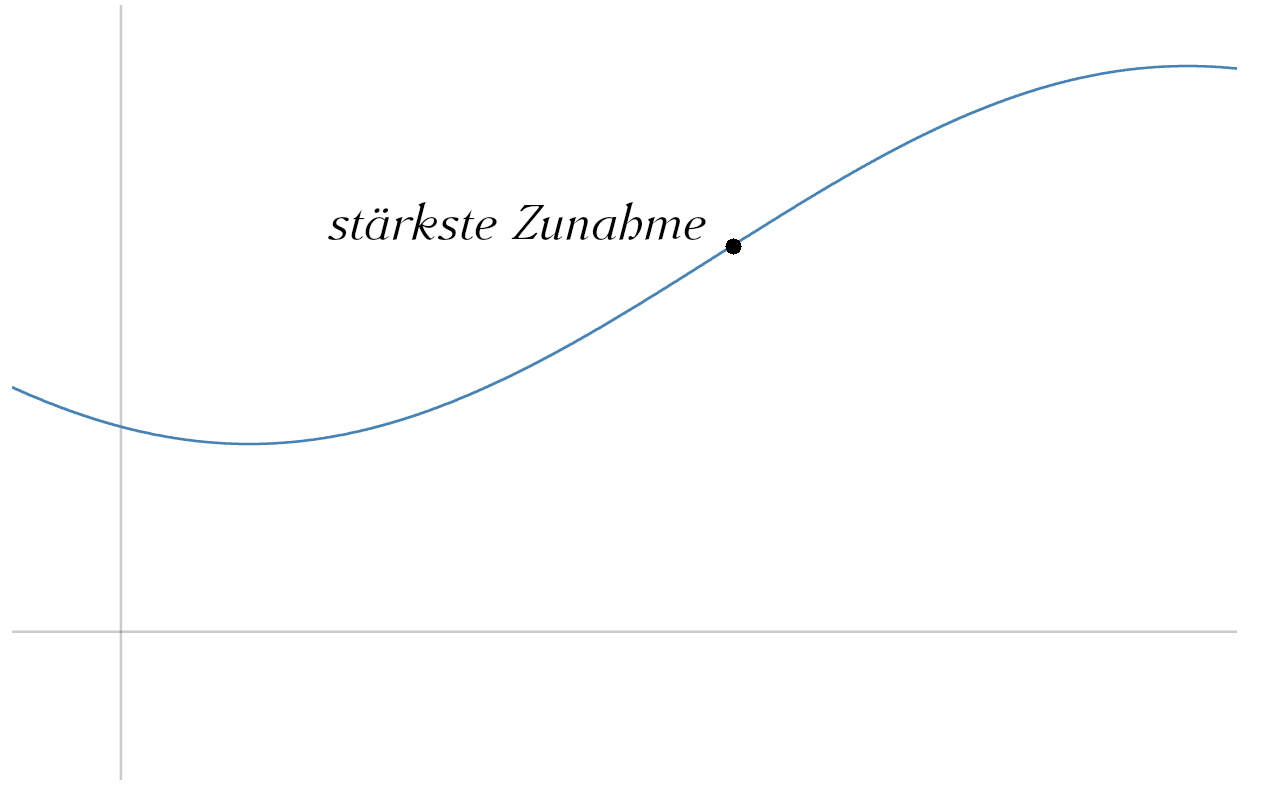
Bedingungen für das Ermitteln von einem Wendepunkt
1. Notwendige Bedingung:
\(f''(x_W)=0\)
\(\implies\)
potentieller Wendepunkt
2. Hinreichende Bedingung:
\(f''(x_W)=0\)
und
\(f'''(x_W)\ne 0\)
\(\implies\)
Wendepunkt bei \(x_W\)
Beispiel Aufgabe Wendepunkt berechnen:
Untersuche die Funktion
\(f(x)=\frac{1}{4}x^3-\frac{3}{2}x^2+3x-1\)
auf Wendepunkte.
Schritt 1 - Berechne die zweite Ableitung und setze sie gleich Null:
\(f'(x)=\frac{3}{4}x^2-3x+3\)
\(f''(x)=\frac{3}{2}x-3=0\)
Löst man die Nullstellen der zweiten Ableitung, dann erhält man als potentiellen Wendepunkt \(x_W=2\).
Schritt 2 - Berechne die dritte Ableitung und setze \(x_W\) ein:
\(f'''(x)=\frac{3}{2}\)
Da die dritte Ableitung von \(x\) unabhängig ist, können wir da nix einsetzten. Trotzdem ist \(f'''(x)=\frac{3}{2}\gt 0\). Das heißt, \(x_W=2\) ist eine Wendestelle, um genau zu sein eine Rechts-links-Wendestelle.
Um den Funktionswert an der Wendestelle zu ermitteln, setzen wir \(x_W\) in die Funktion ein und erhalten:
\(f(x_W)=\frac{1}{4}\cdot 2^3-\frac{3}{2}\cdot 2^2+3\cdot 2-1=1\)
Die Funktion besitzt am Punkt \(P(2|1)\) eine Rechts-links-Wendestelle.
Mit dem Online Rechner kannst du im Rahmen einer Kurvendiskussion auch die Wendepunkte einer Funktion berechnen.
Sattelpunkt berechnen
Ein Sattelpunkt ist ein Wendepunkt jedoch mit einer Steigung von null.
Bedingungen für das Ermitteln von einem Sattelpunkt
1. Notwendige Bedingung:
\(f'(x_s)=0\)
\(f''(x_s)=0\)
\(\implies\)
potentieller Wendepunkt bei \(x_s\)
2. Hinreichende Bedingung:
\(f'''(x_s)\ne 0\)
\(\implies\)
Sattelpunkt bei \(x_s\)
Bei einem Sattelpunkt müssen die gleichen Bedingungen erfüllt sein wie bei einem Wendpunkt und zusätzlich muss die erste Ableitung am Sattelpunkt gleich null sein.
Du kannst den Sattelpunkt einer Funktion mit dem Kurvendiskussion Rechner berechnen.
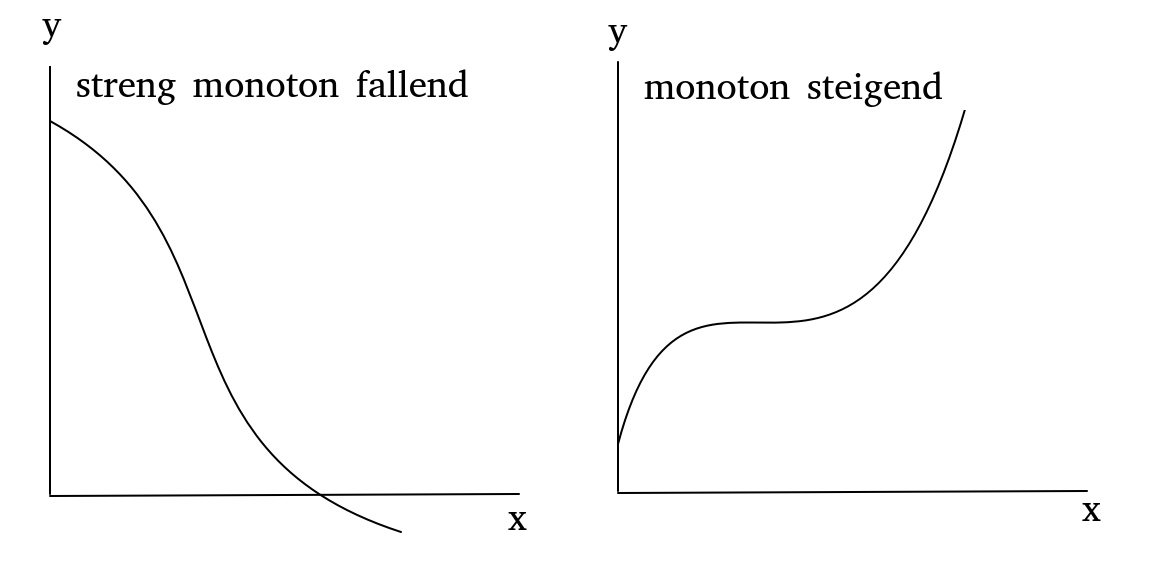
Monotonieverhalten
Das Monotonieverhalten sagt einem ob es sich um eine steigende oder fallende Funktion handelt. Um eine Aussage über das Monotonieverhalten zu treffen betrachtet man die erste Ableitung \(f'(x)\) der Funktion.
Wie wir bereits wissen gibt uns \(f'(x)\) die Steigung der Funktion an:
- \(f'(x)\geq 0\)
- \(f'(x)\leq 0\)
- \(f'(x)\gt 0\)
- \(f'(x)\lt 0\)
\(\implies f(x)\) ist monoton steigend
\(\implies f(x)\) ist monoton fallend
\(\implies f(x)\) ist sterng monoton steigend
\(\implies f(x)\) ist sterng monoton fallend
Achtung !
Der Unterscheid zwischen monoton und streng monoton ist wichtig.
Streng monoton bedeutet, dass die Steigungsfunktion \(f'(x)\) an keiner Stelle den Wert \(0\) annimmt.
Krümmungsverhalten
Um das Krümmungsverhalten einer Funktion zu bestimmen verwendet man die zweite Ableitung \(f''(x)\).
Dabei Gilt:
\(f''(x)\gt 0\)
\(\implies f(x)\) ist links gekrümmt
\(f''(x)\lt 0\)
\(\implies f(x)\) ist rechts gekrümmt
Symmetrieverhalten
Symmetrie von ganzrationalen Funktionen:
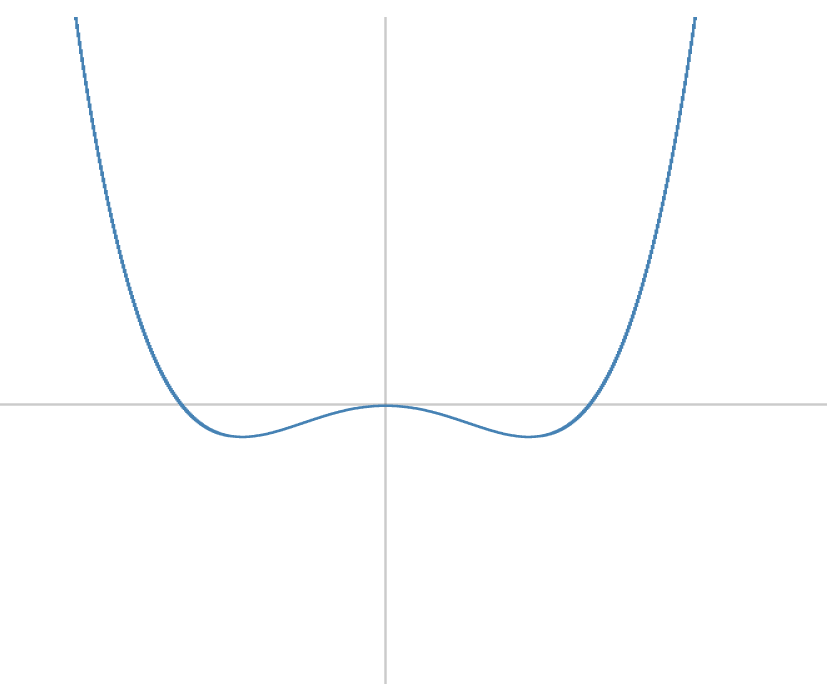
Besteht die Funktion nur aus geraden Exponenten wie beispielsweise
\(f(x)=x^4-x^2\)
dann ist die Funktion achsensymmetrisch zur y-Achse.
Rechnerisch wird das folgendermaßen gezeigt:
\(f(-x)=f(x)\)
\(\begin{aligned} f(-x)&=(-x)^4-(-x)^2\\ &=x^4-x^2=f(x) \end{aligned}\)
Bedingung für Achensymmetrie
\(f(-x)=f(x)\)
Besteht die Funktion nur aus ungeraden Exponenten wie beispielsweise
\(f(x)=x^3-3x\)
dann ist die Funktion punktsymmetrisch zum Ursprung.
Rechnerisch wird das folgendermaßen gezeigt:
\(f(-x)=-f(x)\)
\(\begin{aligned} f(-x)&=(-x)^3-3(-x)\\ &=-x^3+3x=-f(x) \end{aligned}\)
Bedingung für Punktsymmetrie
\(f(-x)=-f(x)\)
