Quadratische Funktionen Übersicht
Quadratische Funktion Rechner
Mit dem Online Rechner von Simplexy kannst du ganz einfach eine quadratische Funktion bzw. eine Parabel zeichnen, die Nullstellen berechnen, die Schnittpunkte berechnen und viel mehr.
Quadratische Funktion
Übersicht
Das Merkmal einer quadratischen Funktion besteht darin, dass der höchste Exponent eine \(2\) ist.
Die allgemeine Form einer quadratischen Funktion lautet:
\(\begin{aligned} f(x)=ax^2+bx+c \end{aligned}\)
Ganz wichtig ist dabei, das der Parameter a nicht Null ist. Den Term \(ax^2\) nennt man quadratisches Glied, \(bx\) heißt lineares Gleid und \(c\) wird als das absolutes Glied bezeichnet. Der Graph einer quadratischen Funktion wird Parabel genannt.
Beispiele für quadratische Funktionen
- \(f(x)=x^2\)
- \(f(x)=x^2+x\)
- \(f(x)=x^2+5\)
- \(f(x)=x^2-2x+1\)
- \(f(x)=-\frac{1}{2}\cdot x^2+2x+\frac{1}{4}\)
Der Graph einer quadratischen Funktion wird Parabel genannt. Eine Parabel kann sowohl nach oben als auch nach unten geöffnet sein. Eine Parabel ist immer symmetrisch, dabei verläuft die Symmetrieachse parallel zur \(y\)-Achse. Der Schnittpunkt der Parabel mit ihrer Symmetrieachse wird Scheitelpunkt genannt. Eine Parabel kann bis zu zwei Schnittpunkte mit der \(x\)-Achse besitzen, diese Schnittpunkte werden Nullstellen genannt. Übrigens kann eine Parabel auch keine Nullstellen besitzen. Mehr dazu weiter unten...
Normalform einer Parabel
Die allgemeine Form oder auch Normalform einer quadratischen Funktion lautet:
\(\begin{aligned} f(x)=ax^2+bx+c \end{aligned}\)
Beispiele für Parabeln
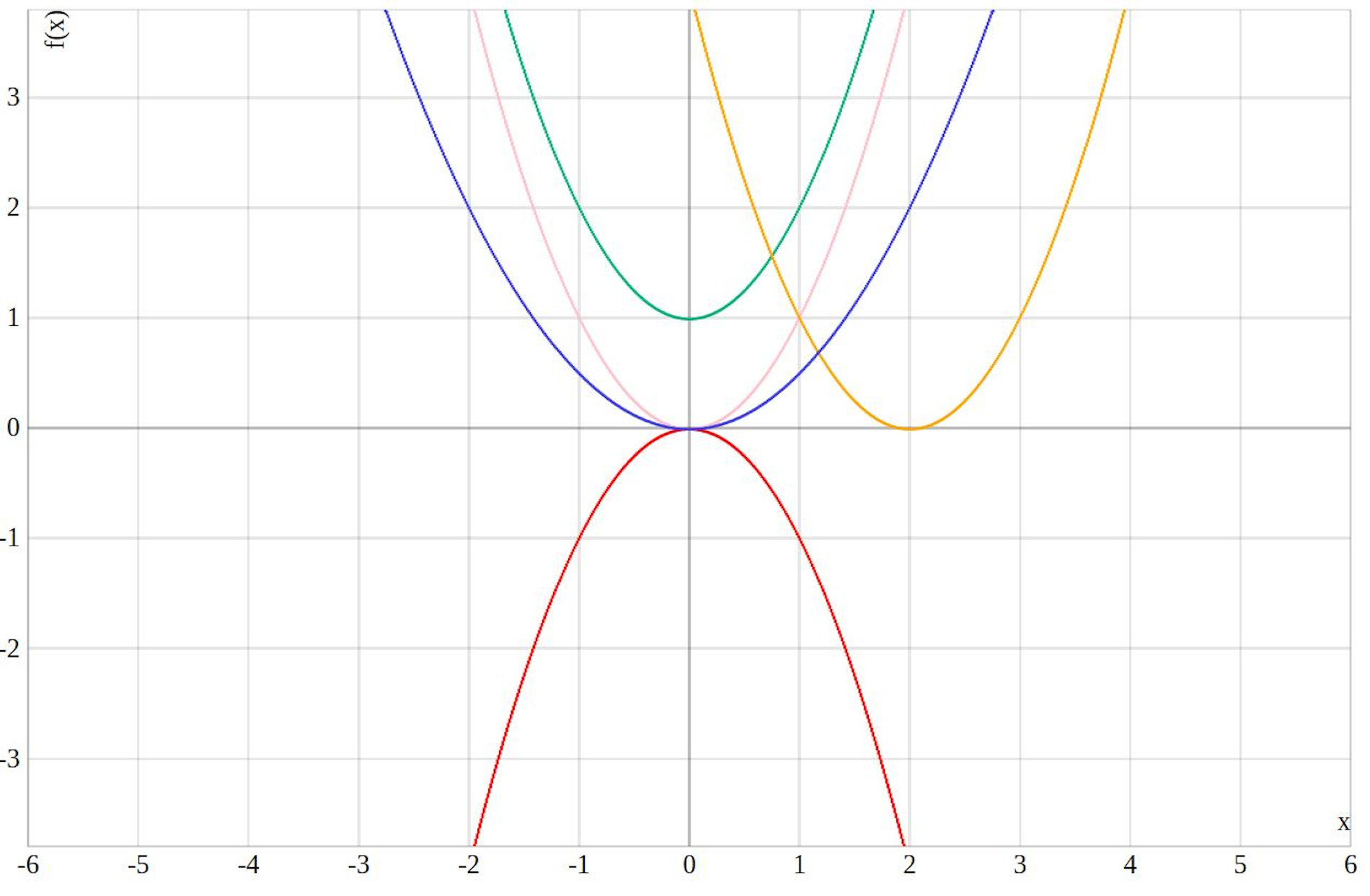
Solche Graphen kannst du mit dem Online Rechner von Simplexy selber erstellen, gib eine Parabel in das Eingabefeld ein und siehe was passiert. Simplexy bietet auch einen Nullstellen Rechner und ein qp-Formel Rechner mit Rechenweg an. Gib dazu am besten zur Probe mal \(x^2+2x-5=0\) ein, du erhältst die Nullstellen und den Rechenweg.
Normalparabel
Den Begriff Normalparabel verwendet man für die quadratische Funktion
\(f(x)=x^2\). Ihr Scheitelpunkt befindet sich am Punkt \((0,0)\) und die Nullstelle liegt bei \(x_{0}=0\). Der Graph der Normalparabel ist unten dargestellt.
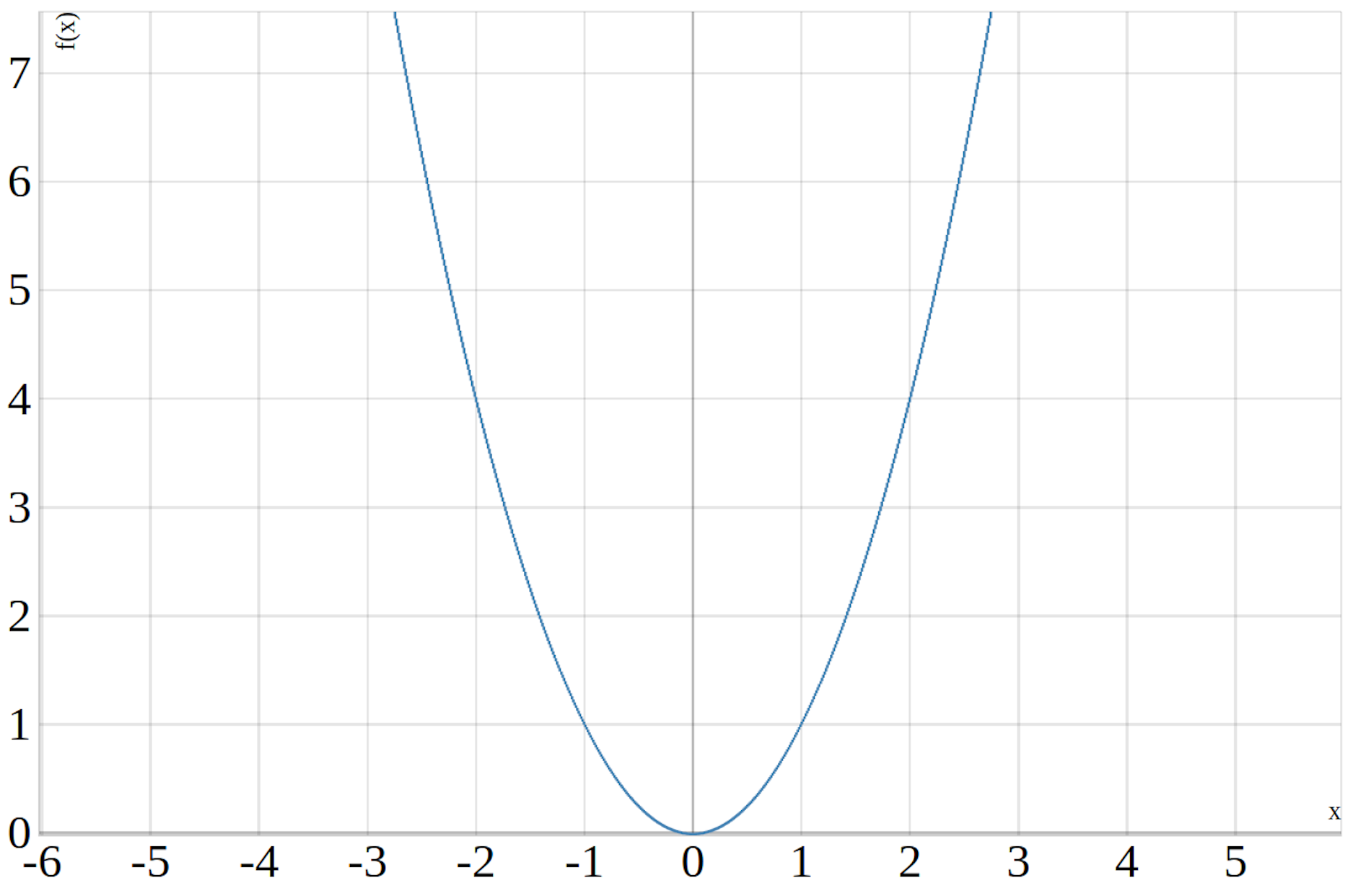
Mehr zum Thema Normalparabel findest du im Beitrag Normalparabel.
Vorzeichen einer Parabel
Ein Minus vor dem Term \(x^2\) führt dazu, dass die Parabel nach unten geöffnet ist. Die Funktion \(f(x)=-x^2\) ist eine Parabel die an der \(x\)-Achse gespiegelt ist. Wichtig ist dabei, dass das Minuszeichen nicht mit quadriert wird, sonst gilt:
\(f(x)=(-x)^2=x^2\)
denn
\(-x\cdot -x = x^2\)
Die nach unten geöffnete Parabel ist in der folgenden Abbildung dargestellt:
\(\begin{aligned} f(x)=-x^2 \end{aligned}\)
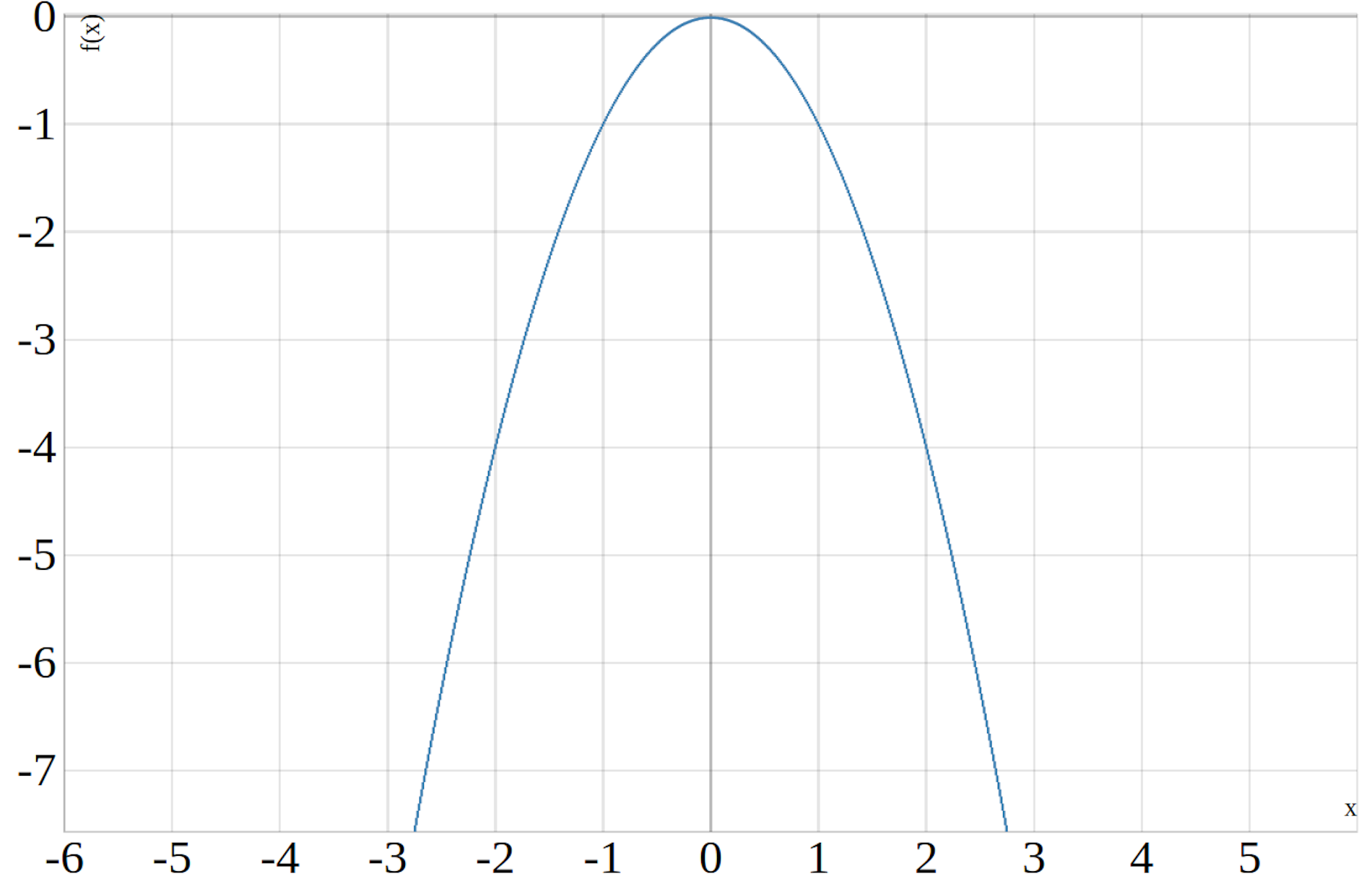
Mehr zum Thema negative Parabel findest du im Beitrag negative Parabel.
Verschiebung in y Richtung
Mit dem Parameter \(c\) in der Funktionsgleichung einer quadratischen Funktion \(f(x)=x^2+c\) kann die Parabel entlang der y-Achse verschoben werden. Eine Verschiebung entlang der y Achse entspricht einer Verschiebung der Parabel nach oben oder unten.
Verschiebung in y Richtung
Verschiebung entlang der \(y\)-Achse:
\(f(x)=x^2+c\)
- Ist \(c\) größer als Null, dann wird die Parabel nach oben verschoben.
- Ist \(c\) kleiner als Null, dann wird die Parabel nach unten verschoben.
Im unteren Graph siehst du eine Parabel die nach oben verschoben ist (blau) und eine Parabel die nach unten verschoben ist (rot).
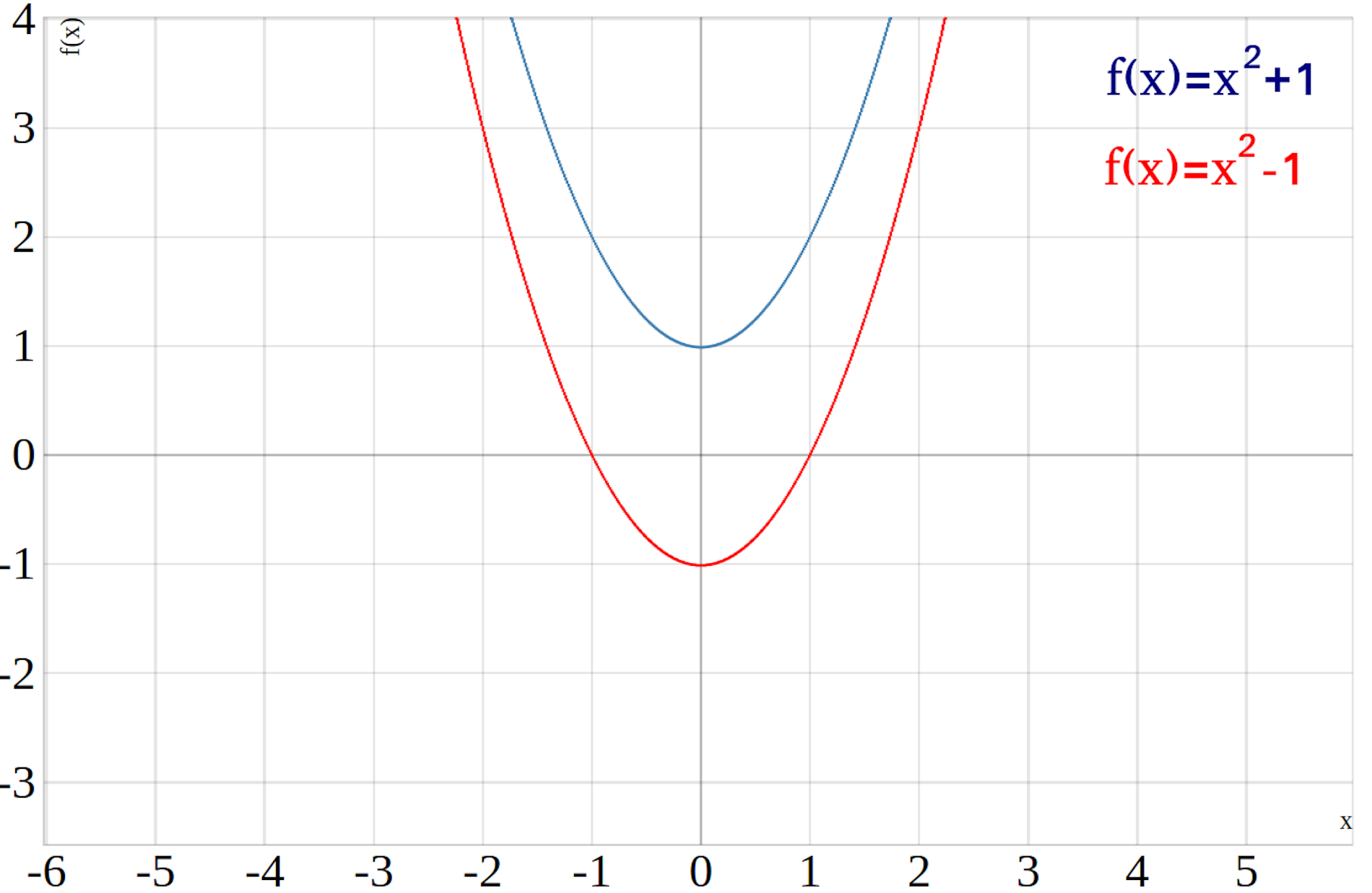
Mehr zum Thema Parabel entlang der y Achse verschieben, findest du im Beitrag Parabel nach oben und unten verschieben.
Verschiebung in x Richtung
Um eine quadratischen Funktion entlang der x-Achse zu verschieben, muss man den Parameter \(d\) in der Parabel \(f(x)=(x+d)^2\) verändern.
Verschiebung in x Richtung
Verschiebung entlang der \(x\)-Achse:
\(f(x)=(x+d)^2\)
- Ist \(d\) größer als Null, dann wird die Parabel nach links verschoben.
- Ist \(d\) kleiner als Null, dann wird die Parabel nach rechts verschoben.
Im unteren Bild siehst du eine quadratische Funktion die nach links verschoben ist (blau) und eine Parabel die nach rechts verschoben ist (rot).
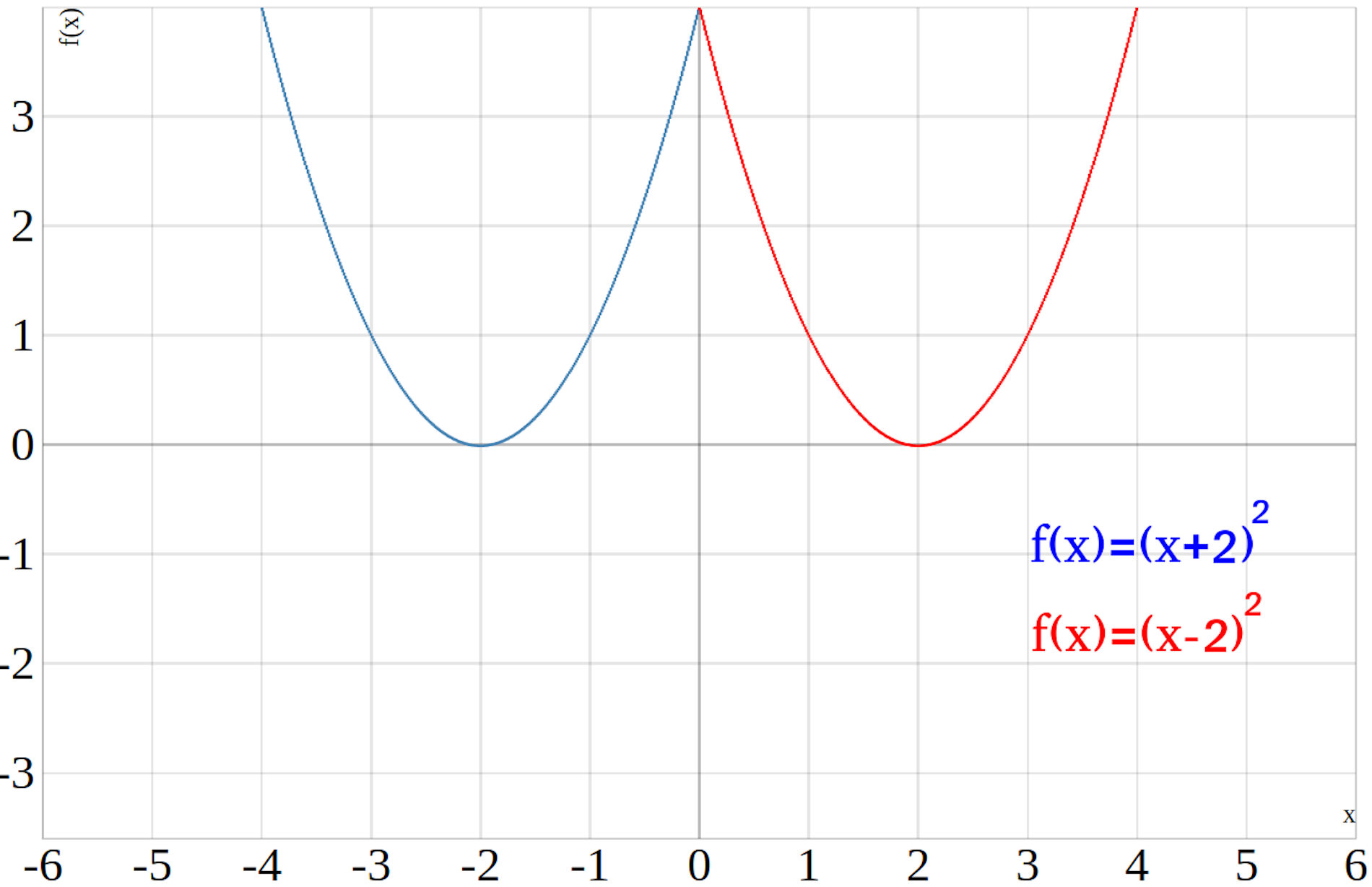
Mehr zum Thema Parabel entlang der x Achse verschieben, findest du im Beitrag Parabel nach links und rechts verschieben.
Streckung und Stauchung
Eine Parabel kann gestaucht oder gestreckt werden, mit dem Parameter \(a\) im Term \(f(x)=ax^2\) kann Einfluss auf die Stauchung und Streckung der Parabel genommen werden. Wenn \(a\) zwischen \(0\) und \(1\) liegt, dann wird die Parabel gestaucht. Ist \(a\) größer als \(1\), so wird die Parabel gestreckt.
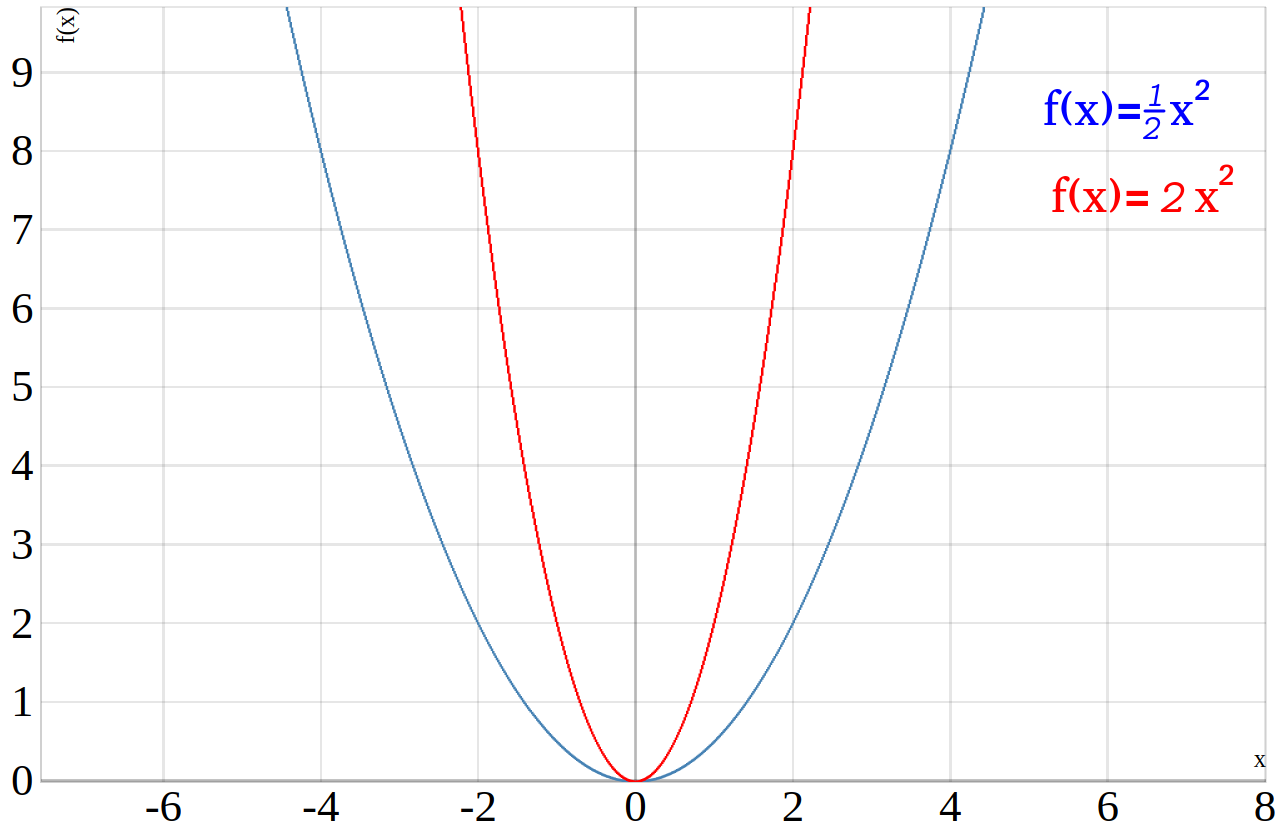
In dem Beitrag Parabel Streckung und Parabel Stauchung findest du mehr Beispiele.
Quadratische Funktion Scheitelpunkt
Der Scheitelpunkt einer quadratischen Funktion lässt sich mit Hilfe einer allgemeinen Formel sehr leicht berechnen. Für eine allgemeine Parabel mit der Funktionsgleichung
\(\begin{aligned} f(x)=ax^2+bx+c \end{aligned}\)
liegt der Scheitelpunkt bei den Koordinaten
\(\begin{aligned} \Big(\frac{-b}{2a}\,\,\Big|\,\,\frac{4ac-b^2}{4a}\Big) \end{aligned}\)
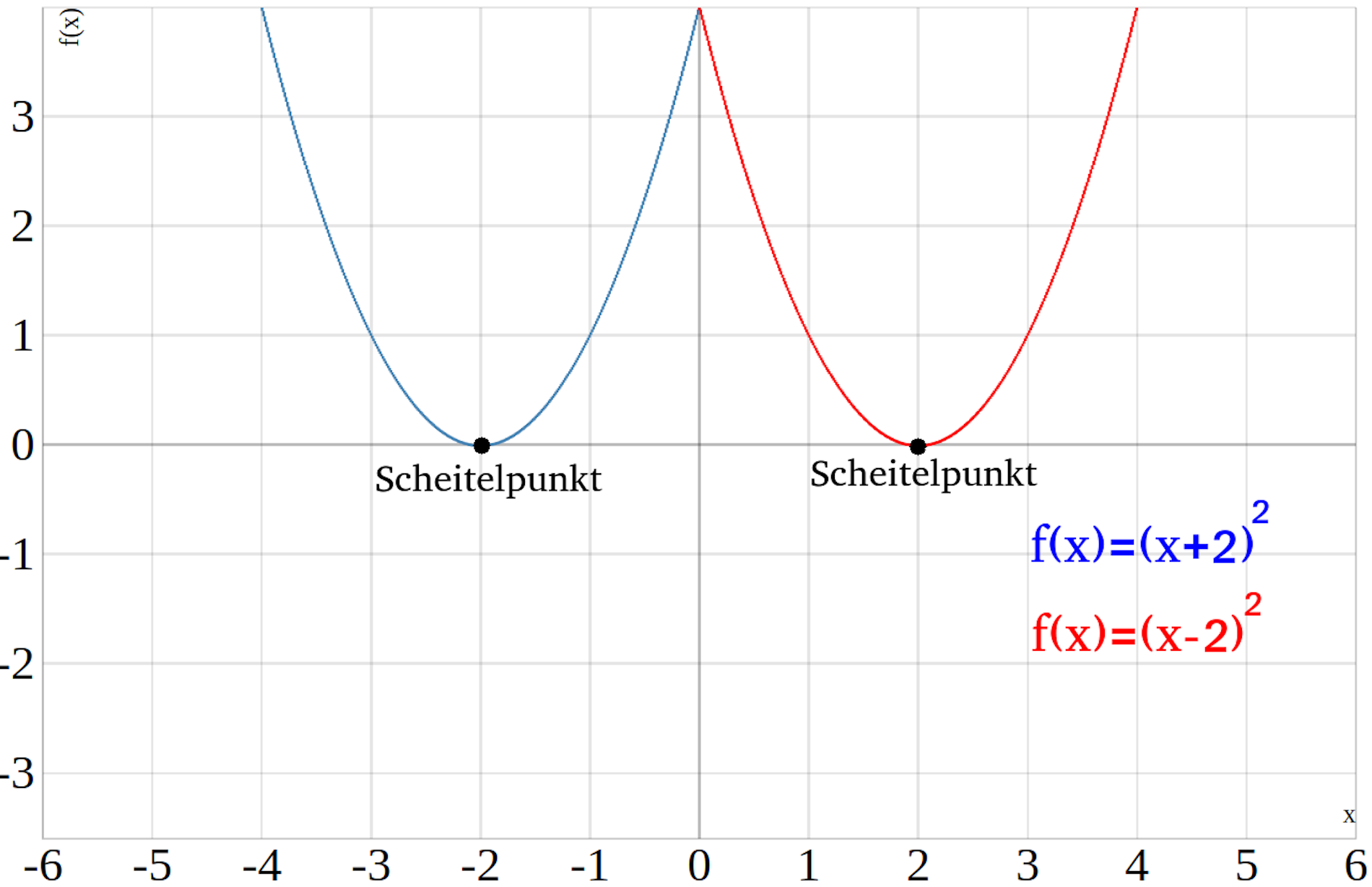
Quadratische Funktion Scheitelpunkt berechnen
Der Scheitelpunkt einer quadratischen Funktion der Form
\(\begin{aligned} f(x)=ax^2+bx+c \end{aligned}\)
besitzt die Koordinaten
\(\begin{aligned} S=\Big(\frac{-b}{2a}\,\,\Big|\,\,\frac{4ac-b^2}{4a}\Big) \end{aligned}\)
Eine quadratische Funktion kann in zwei Formen mathematisch dargestellt werden. Es gibt die Normalform einer Parabel und die Scheitelpunktform einer Parabel. Man kann jede quadratische Funktion sowohl in der Normalform als auch in der Scheitelpunktform angeben. Ist einem, eine quadratische Funktion in der Normalform gegeben, so kann man diese in die Scheitelpunktform überführen. Genauso kann man auch einen Parabel von der Scheitelpunktform in die Normalform umrechnen. Der Graph (das Aussehen) einer Parabel ist unabhängig davon, in welcher Form die Funktionsgleichung angegben ist. Es handelt sich bei der Normalform und der Scheitelpunktform lediglich um mathematische Schreibweisen.
Normalform und Scheitelpunktform einer quadratischen Funktion
Scheitelpunktform
Normalform
\(f(x)=a(x+d)^2+e\)
\(f(x)=ax^2+bx+c\)
Die Scheitelpunktform einer quadratischen Funktion bestizt gegenüber der Normalform einen Vorteil, wenn es darum geht den Scheitelpunkt der Parabel zu ermitteln. As der Scheitelpunktform können die Koordinaten des Scheitelpunktes direkt abgelesen werden.
Scheitelpunktform einer quadratischen Funtion
Die Scheitelpunktform einer quadratischen Funktion lautet:
Scheitelpunktform
\(f(x)=a(x\textcolor{blue}{+}\textcolor{red}{d})^2\textcolor{green}{+e}\)
Die Koordinaten des Scheitelpunktes können direkt abgelesen werden. Der Scheitelpunkt befindet sich bei:
\(S(\textcolor{blue}{-}\textcolor{red}{d}|\textcolor{green}{e})\)
Achtung!
Ein \(\textcolor{blue}{+}\textcolor{red}{d}\) in der Scheitelpunktform führt dazu, dass der \(x\)-Wert des Scheitelpunkts bei \(\textcolor{blue}{-}\textcolor{red}{d}\) liegt. Hier ist es mit den Vorzeichen genau umgekehrt. Mehr dazu im Video und im Beitrag zur Scheitelpunktform.
Möchtest du wissen, wie man eine Parabel von der Scheitelpunktform in die Normalform umrechnen kann?
Dann wirf einen Blick auf den Beitrag Scheitelpunktform in Normalform umrechnen.
Quadratische Funktion - Nullstellen
Um die Nullstellen einer quadratischen Funktion berechnen zu können, muss man die Funktionsgleichung Nullsetzen.
\(\begin{aligned} x^2+px+q=0 \end{aligned}\)
Die Lösung dieser Gleichung erhälts du mit der pq-Formel oder der Mitternachtsformel.
pq-Formel
\(\begin{aligned} x_{1/2}=-\frac{p}{2}\pm\sqrt{\Big(\frac{p}{2}\Big)^2-q} \end{aligned}\)
Wie du siehst steht in der pq-Formel \(x_{1/2}\) weil eine quadratische Funktion bis zu zwei Nullstellen bestizen kann. Eine quadratische Funktion kann keine, eine oder zwei Nullstellen besitzen. Um die Anzahl an Nullstellen zu bekommen musst du die Diskriminante
\(\begin{aligned} D=\Big(\frac{p}{2}\Big)^2-q \end{aligned}\)
berechnen, dass ist der Term unter der Wurzel in der pq-Formel. Es gilt:
- Wenn \(D\) kleiner als null ist, dann existieren keine Nullstellen.
- Wenn \(D=0\) ist, dann existiert genau eine Nullstelle.
- Wenn \(D\) größer als null ist, dann existieren zwei Nullstellen.
In dem unteren Graph sind zwei Parabeln abgebildet, die blaue Parabel besitzt keine Nullstellen während die rote Parabel zwei Nullstellen besitzt.
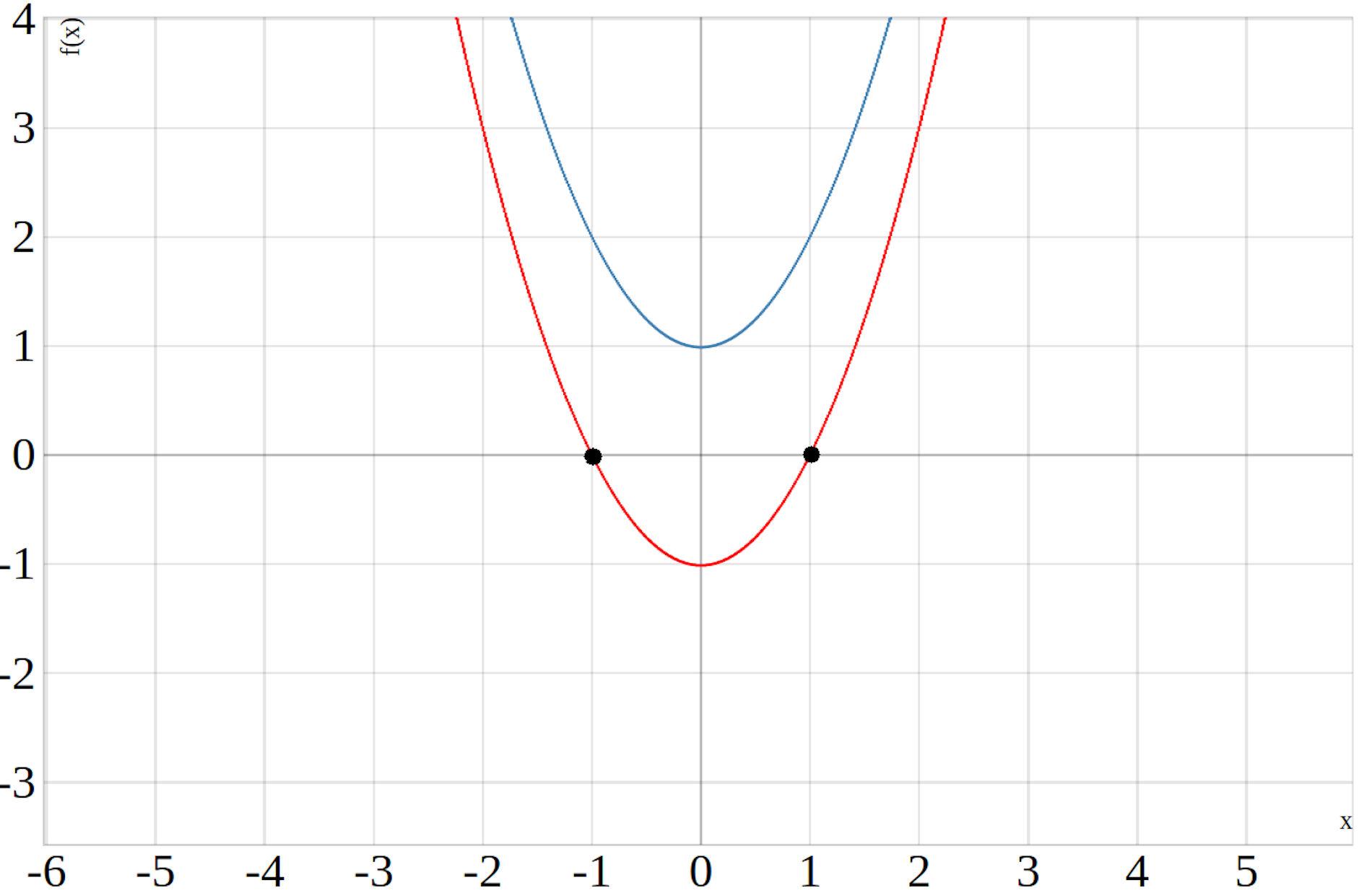
Quadratische Funktion Nullstellen berechnen
Eine quadratische Funktion kann keine, eine oder zwei Nullstellen besitzen.
Die Nullstellen von \(f(x)=ax^2+bx+c\) berechnen sich mit der
Mitternachtsformel
\(\begin{aligned} x_{1/2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{aligned}\)
Fallunterscheidung
\(\begin{aligned} x_{1}=\frac{-b-\sqrt{b^2-4ac}}{2a} \end{aligned}\)
\(\begin{aligned} x_{2}=\frac{-b+\sqrt{b^2-4ac}}{2a} \end{aligned}\)
Mit dem Rechner von Simplexy kannst du Nullstellen quadratischer Funktionen berechen. Gib dazu am besten zur Probe mal \(x^2+2x-5=0\) ein, du erhältst die Nullstellen und den Rechenweg.
Hier kommst du zum Rechner.
Wenn du mehr zum Thema Mitternachtsformel bzw. pq-Formel lernen möchtest, dann werf einen Blick auf den Beitrag Mitternachtsformel bzw. pq-Formel.
Vorgehen um Nullstellen von Parabeln zu berechnen:
Quadratische Funktion in die Normalform bringen.
\(a,b\) und \(c\) aus der Normalform ablesen.
\(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
Mitternachtsformel ausrechnen.
Parabel Nullstellen berechen Beispiele
Beispiel 1:
\(f(x)=2x^2-12x-14\)
Die Funktion befindet sich bereits in der Normalform. Wir können also direkt zum zweiten Schritt übergehen und \(a,b\) und \(c\) ablesen.
\(a=2,\) \(b=-12\) und \(c=-14\)
Nun müssen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-(-12)\pm\sqrt{(-12)^2-4\cdot 2\cdot (-14)}}{2\cdot 2}\\ \\ &=\frac{12\pm\sqrt{144+112}}{4}\\ \\ &=\frac{12\pm\sqrt{256}}{4}\\ \\ &=\frac{12\pm 16}{4}\\ \end{aligned}\)
Fallunterscheidung:
\(x_{1}=\)\(\frac{12-16}{4}\)\(=-1\)
\(x_{2}=\)\(\frac{12+16}{4}\)\(=7\)
Die Nullstellen der Parabel befinden sich somit bei
\(x_1=-1\) und \(x_2=7\).
Beispiel 2:
\(f(x)=4x^2-16x+16\)
Die Funktion befindet sich bereits in der Normalform. Wir können also direkt zum zweiten Schritt übergehen und \(a,b\) und \(c\) ablesen.
\(a=4,\) \(b=-16\) und \(c=16\)
Nun müssen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-(-16)\pm\sqrt{(-16)^2-4\cdot 4\cdot 16}}{2\cdot 4}\\ \\ &=\frac{16\pm\sqrt{256-256}}{8}\\ \\ &=\frac{16\pm\textcolor{blue}{\sqrt{0}}}{8}\\ \\ &=\frac{16\pm 0}{8}\\ \\ &=\frac{16}{8}\\ \\ &=2\\ \end{aligned}\)
In diesem Beispiel hat die Parabel nur eine Nullstelle, da
die Diskriminante \(D\) gleich Null ist.
\(D=b^2-4ac=0\)
Die einzige Nullstelle befindet sich bei \(x_0=2\).
Beispiel 3:
\(f(x)=2x^2-8x+11\)
Die Funktion befindet sich bereits in der Normalform. Wir können also direkt zum zweiten Schritt übergehen und \(a,b\) und \(c\) ablesen.
\(a=2,\) \(b=-8\) und \(c=11\)
Nun müssen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ &=\frac{-(-8)\pm\sqrt{(-8)^2-4\cdot 2\cdot 11}}{2\cdot 2}\\ &=\frac{8\pm\sqrt{64-88}}{4}\\ &=\frac{16\pm\textcolor{red}{\sqrt{-24}}}{4}\\ \end{aligned}\)
In diesem Beispiel hat die Parabel keine Nullstelle. Die Wurzel einer negativen Zahl ist in den reellen Zahlen nicht definiert. Aus diesem Grund hat die quadratische Funktionen keine Nullstellen. Sie befindet sich oberhalb der \(x-\)Achse.
