Fläche zwischen zwei Graphen und der x-Achse berechnen
Integralrechner
Mit dem Integral Rechner von Simplexy kannst du sowohl bestimmte als auch unbestimmte Integrale berechnen. Teste den Rechner jetzt aus...
Eingeschlossene Fläche zwischen zwei Funktionen und der x-Achse
Wie man die Fläche zwischen zwei Graphen und der x-Achse berechnen kann, sehen wir uns direkt an einem Beispiel an.
Gegeben sind die zwei Funktionen
\(\begin{aligned} f(x)&=-x^2+2x+3\\ \\ g(x)&=-2x+3 \end{aligned}\)
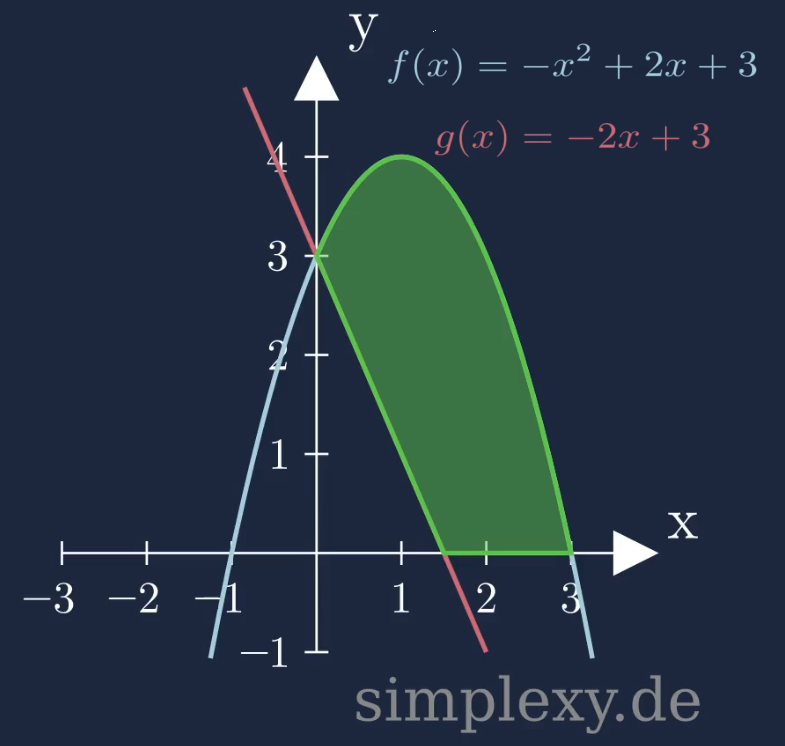
Um die grün markierte Fläche zwischen den zwei Funktionen und der x-Achse berechnen zu können, muss man sich überlegen wie diese Fläche zusammengesetzt ist. Dazu benötigt man jedoch den Schnittpunkt der zwei Funktionen und die Nullstellen der Funktionen. Diese Punkte sind im unteren Bild markiert.
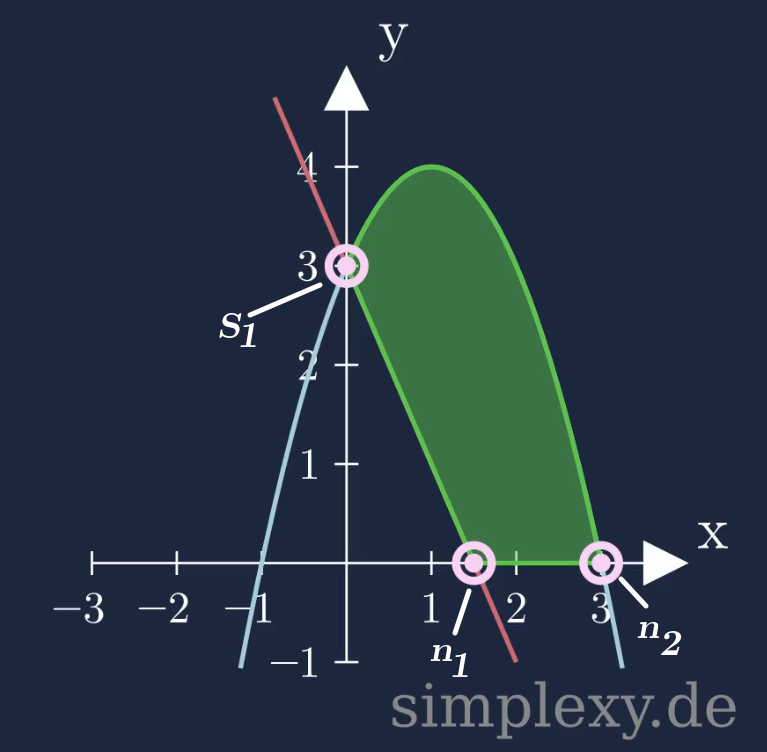
Um die eingeschlossene Fläche zwischen den zwei Funktionen und der x-Achse zu berechnen, müssen wir sowohl die blau als auch die rote Fläche berechnen.
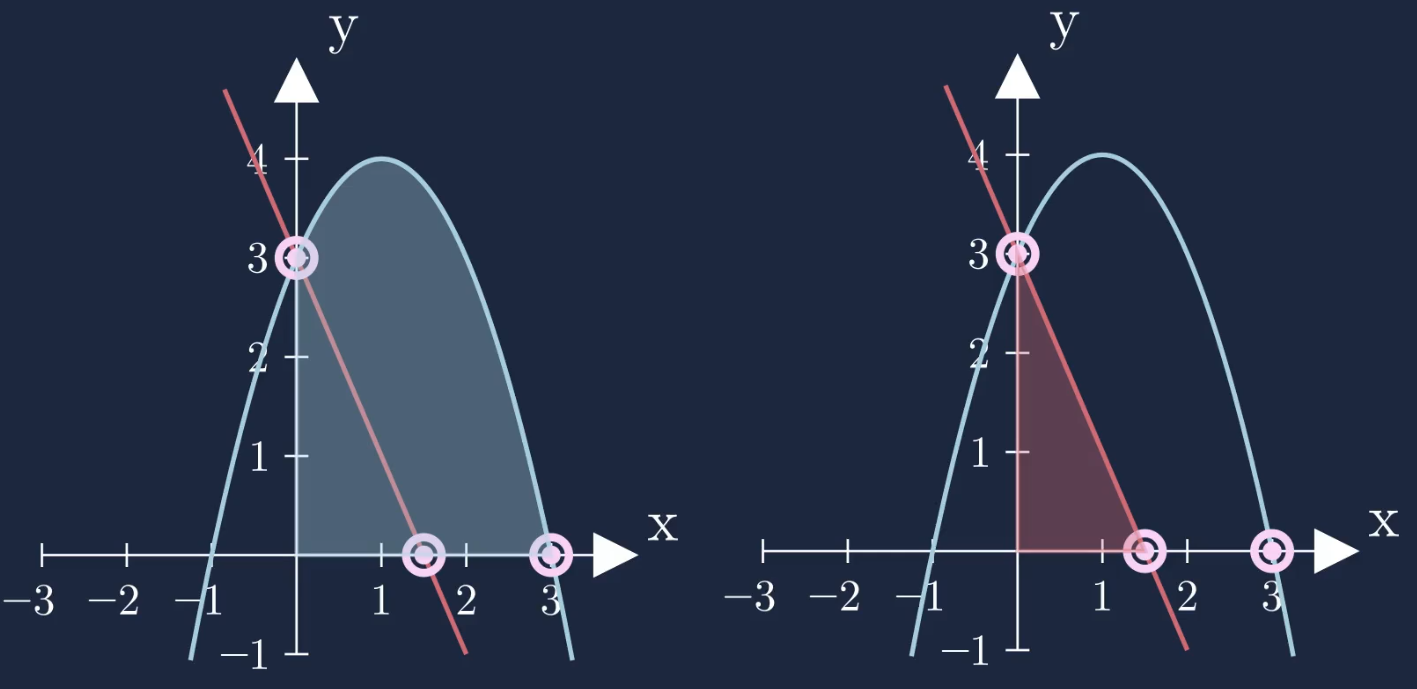
Bildet man die differenz dieser zwei Flächen, so erhält man die gesuchte grüne Fläche zwischen den zwei Funktionen und der x-Achse.
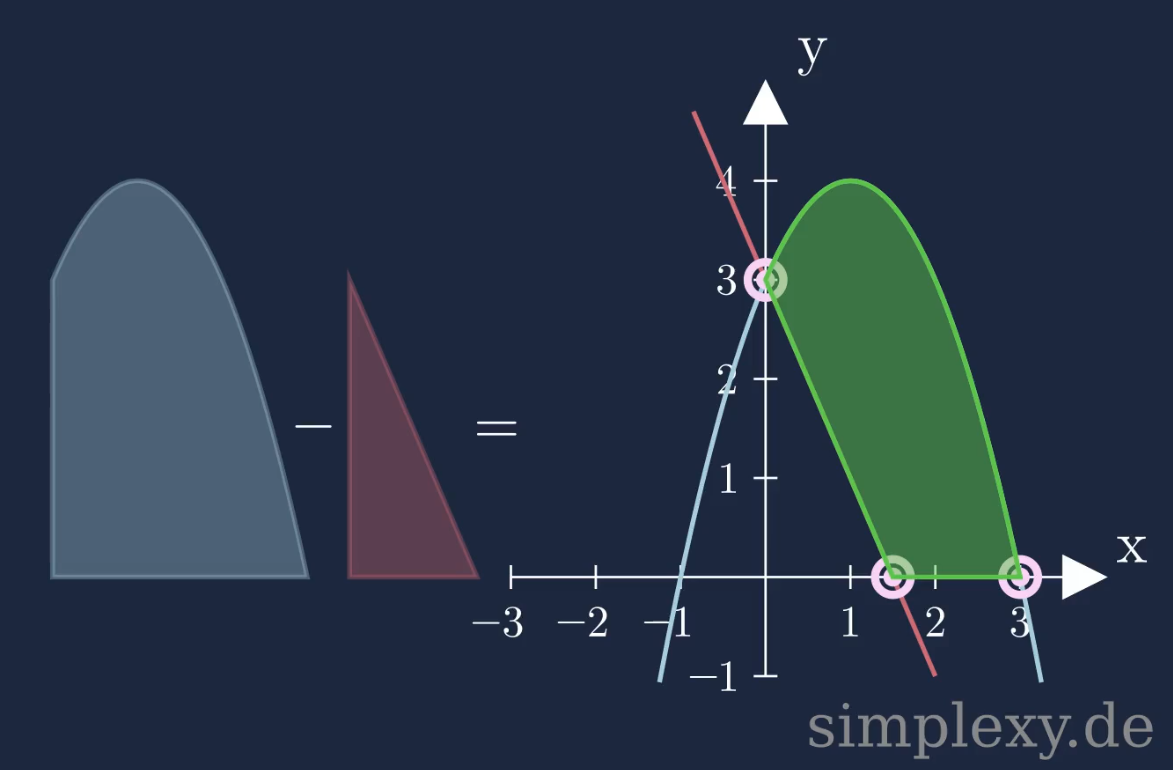
Um die grüne Fläche zwischen den zwei Funktionen zu berechnen, müssen wir also folgende Schritte durchführen.
Schritt 1
Berechne die Schnittpunkte zwischen den zwei Funktionen. Die Schnittpunkte erhält man, durch gleichsetzen der zwei Funktionsgleichungen.
\(\begin{aligned} f(x)&=g(x)\\ \\ -x^2+2x+3&=-2x+3\,\,|+2x-3\\ \\ -x^2+2x+3+2x-3&=0\\ \\ -x^2+4x&=0\\ \\ &\implies\\ \\ s_1=0 &\,\,\,\,\&\,\,\,\, s_2=4 \end{aligned}\)
Die zwei Schnittpunkte der Funktionen lauten \(s_1=0\) und \(s_2=4\). Für die Berechnung der Fläche benötigen wir nur den Schnittpunkt \(s_1=0\). Der Schnittpunkt \(s_2=4\) befindet sich unterhalb der x-Achse und ist damit für die Flächenberechnung irrelevant.
Schritt 2
Berechne die Nullstellen der Funktion \(f(x)\) indem die Funktionsgleichung Null gesetzt wird. Die Nullstellen sind mit der Mitternachtsformel oder der pq-Formel zu ermitteln
\(\begin{aligned} f(x)&=0\\ \\ -x^2+2x+3&=0\\ \\ &\implies\\ \\ x_0=-1&\,\,\,\,\&\,\,\,\, x_1=3 \end{aligned}\)
Die Nullstellen der Funktion \(f(x)\) lauten \(x_0=-1\) und \(x_1=3\). Die Nullstelle \(x_0=-1\) ist für die Berechnung der eingeschlossenen Fläche irrelevant. Wichtig ist die Nullstellen \(x_1=3\). Diese Nullstelle wird nun umbenannt zu \(n_2=3\).
Schritte 3
Berechne die Nullstelle der Funktion \(g(x)\).
\(\begin{aligned} g(x)&=0\\ \\ -2x+3&=0\,\,\,|-3\\ \\ -2x&=-3\,\,\,|\cdot -\frac{1}{2}\\ \\ x&=\frac{3}{2}=1,5 \end{aligned}\)
Die Nullstelle der Funktion \(g(x)\) liegt bei \(1,5\). Diese Nullstellen nennen wir \(n_1=1,5\).
Schritt 4
Berechne die blaue Fläche \(\color{blue}{B}\). Wobei dies über das bestimmte Integrale bzgl. der Funktion \(f(x)\) im Intervall \([s_1,n_2]\) berechnet wird.
\(\begin{aligned} \color{blue}{B}&=\displaystyle\int_{s_1}^{n_2}f(x)\,\,dx\\ \\ &=\displaystyle\int_{0}^{3}-x^2+2x+3\,\,dx\\ \\ &=9 \end{aligned}\)
Schritt 5
Berechne die rote Fläche \(\color{red}{C}\). Wobei dies über das bestimmte Integrale bzgl. der Funktion \(g(x)\) im Intervall \([s_1,n_1]\) berechnet wird.
\(\begin{aligned} \color{red}{C}&=\displaystyle\int_{s_1}^{n_1}g(x)\,\,dx\\ \\ &=\displaystyle\int_{0}^{1,5}-2x+3\,\,dx\\ \\ &=\frac{9}{4} \end{aligned}\)
Schritt 6
Um die grüne Fläche \(\color{green}{A}\) zwischen den zwei Funktion und der x-Achse zu erhalten, muss man nur noch die rote Fläche \(\color{red}{C}\) von der blauen Fläche \(\color{blue}{B}\) abziehen.
\(\begin{aligned} {\color{green}{A}}&={\color{blue}{B}}-{\color{red}{C}}\\ \\ &={\color{blue}{9}}-{\color{red}\frac{9}{4}}=\color{green}{\frac{27}{4}} \end{aligned}\)
Damit ist die Fläche zwischen den zwei Funktionen und der x-Achse \(\frac{27}{4}\) Flächeneinheiten groß.
Man hätte auch die blaue Fläche \(\color{blue}{B}\) von der roten Fläche \(\color{red}{C}\) abziehen können. Dann hätte man jedoch den Betrag bilden müssen.
\(\begin{aligned} {\color{green}{A}}&=\Big|{\color{red}{C}}-{\color{blue}{B}}\Big|\\ \\ &=\Big|{\color{red}\frac{9}{4}}-{\color{blue}{9}}\Big|=\color{green}{\frac{27}{4}} \end{aligned}\)
