Gleichungen lösen
Online Rechner für Gleichungen
Mit dem Online Rechner von Simplexy kannst du viele Gleichungen lösen und Gleichungen umstellen. Dabei kannst du dir auch den Rechenweg anzeigen lassen, so kannst du deine eigne Lösung überprüfen.
Gleichungen lösen
Gleichungen lösen zu können, ist eine wichtige Eigenschaft, die man im Laufe der Schulzeit immer wieder benötigen wird. Um Gleichungen lösen zu können, kann man je nachdem mit was für eine Gleichung man es zu tun hat, unterschiedliche Methoden anwenden. Im Laufe des Mathematikunterrichts wird man verschiedene Arten von Gleichungen begegnen. Daher muss man lernen, die jeweiligen Gleichungen voneinander unterscheiden zu können und die richtige Methode zum Lösen anzuwenden. Dieser Beitrag ist ein Überblick zum Thema Gleichungen lösen.
In dem unteren Video kann man sich die Grundlagen zum Gleichungen lösen ansehen. Hier geht es in erster linie darum, wie man eine Gleichung nach x umstellen kann.
Lineare Gleichungen lösen
Eine Lineare Gleichung zeichnet sich daruch aus, dass Sie keine Variable (meisten \(x\)) besitzt mit einem höheren Exponeten als \(1\). Es darf also kein \(x^2\), \(x^3\), \(x^4\), etc. vorkommen.
Beispiel lineare Gleichungen lösen
\(5+x=7\)
Man kann die Gleichung lösen indem man sie genau berachtet. Man kommt nach einiger Zeit darauf, das \(x=2\) sein muss. Dann würde dort stehen:
\(5+2=7\)
die Gleichung wäre damit erfüllt, dass \(x=2\) ist.
Ein anderer Weg mit dem man diese Gleichung lösen kann, besteht darin, dass man sie nach \(x\) umstellt. Dazu Bringen wir die \(5\) auf die rechte Seite, indem wir auf beiden Seiten der Gleichung \(5\) abziehen.
\(\begin{aligned} 5+x&=7\,\,\,|-5\\ 5+x-5&=7-5\\ x&=2 \end{aligned}\)
Diese lineare Gleichung wurde gelöst, indem wir auf beiden Seiten der Gleichung \(5\) abgezogen haben. Das haben wir gemacht, da unser Ziel darin bestand, dass \(x\) auf eine Seite der Gleichung alleine zu bekommen.
Sobald die Variable (meistens \(x\)) alleine auf eine Seite der Gleichung gebracht wurde, ist die Gleichung gelöst.
Hierbei ist es ganz wichtig, dass jede Rechenoperation auf beide Seiten der Gleichung angewandt wird. Beim Gleichungen lösen muss man stets darauf achten, dass sowohl auf der linken Seite als auch auf der rechten Seite der Gleichung die Rechenoperation durchgeführt wird. In unserem Beispiel haben die auf beiden Seiten der Gleichung \(5\) abgezogen. Man darf niemals eine Rechoperation auf nur einer Seite durchführen.
Das kann man sich mit dem folgenden Beispiel besser verdeutlichen.
Wir betrachten die Gleichung
\(5=5\)
Mit diesem Beispiel soll gezeigt werden warum eine Rechenoperation stets auf beide Seiten der Gleichung druchgeführt werden muss.
Wir können nun auf beiden Seiten der Gleichung \(2\) addieren:
\(\begin{aligned} 5&=5\,\,\,|+2\\ 5+2&=5+2\\ 7&=7 \end{aligned}\)
Durch die Addition mit \(2\) steht nun auf beiden Seiten der Gleichung \(7\). Das ist aber eine korrekte Aussage, den \(7\) ist nunmal gleich \(7\).
Stellen Wir uns nun vor, wir hätte die Addition mit \(2\) nur auf der linken Seite der Gleichung durchgeführt.
\(\color{red}\begin{aligned} 5&=5\,\,\,|+2\\ 5+2&=5\\ 7&\neq5 \end{aligned}\)
Wir erhalten auf der linken Seite eine \(7\) und auf der rechten Seite eine \(5\). Das darf bei einer Gleichung nie der Fall sein. Die linke und die rechte Seite einer Gleichung müssen stets gleich sein. Immerhin steht ein \(=\) Zeichen zwischen ihnen.
Regel
Beim Gleichungen lösen und beim Gleichungen umstellen muss jede Rechenoperation die man durchführt stets auf beiden Seiten der Gleichung angewandt werden. Nur so ist gewährleistet, das beide Seiten der Gleichung stets gleich sind.
Weiteres Beispiel zum lösen von Gleichungen
\(\color{blue}\begin{aligned} x-3&=5\\ x-3&=5\,\,\,\,|+3\\ x-3+3&=5+3\\ x&=8 \end{aligned}\)
Abgesehen von Addition und Subtraktion kann in einer Gleichung auch eine Multiplikation vorkommen.
Beispiel für Gleichungen mit Multiplikation
\(\begin{aligned} x\cdot 5&=10\\ \\ x\cdot 5&=10 \,\,\,\,\,|:5\\ \\ \frac{x\cdot 5}{5}&=\frac{10}{5}\\ \\ x&=2 \end{aligned}\)
Beim lösen dieser Gleichung haben wir beide Seiten der Gleichung durch \(5\) geteilt. Damit blieb \(x\) auf der linken Seite alleine stehen.
So ähnlich funktioniert es auch wenn in einer Gleichung ein Bruch vorkommt.
Beispiel für Gleichungen mit Brüchen
\(\begin{aligned} \frac{x}{2}&=20\\ \\ \frac{x}{2}&=20 \,\,\,\,\,|\cdot 2\\ \\ \frac{x}{2} \cdot 2&=20\cdot 2\\ \\ x&=40 \end{aligned}\)
Gleichungen lösen ist nicht schwer. Man muss nur dafür sorgen, dass die Variable auf einer Seite alleine stehen bleibt. Um das zu erreichen, wendet man verschiedene Rechenoperationen an. Dabei ist es wichtig, darauf zu achten, dass die Rechenoperationen auf beiden Seiten der Gleichung angewandt werden.
Weitere Beispiele zum lösen von Gleichungen
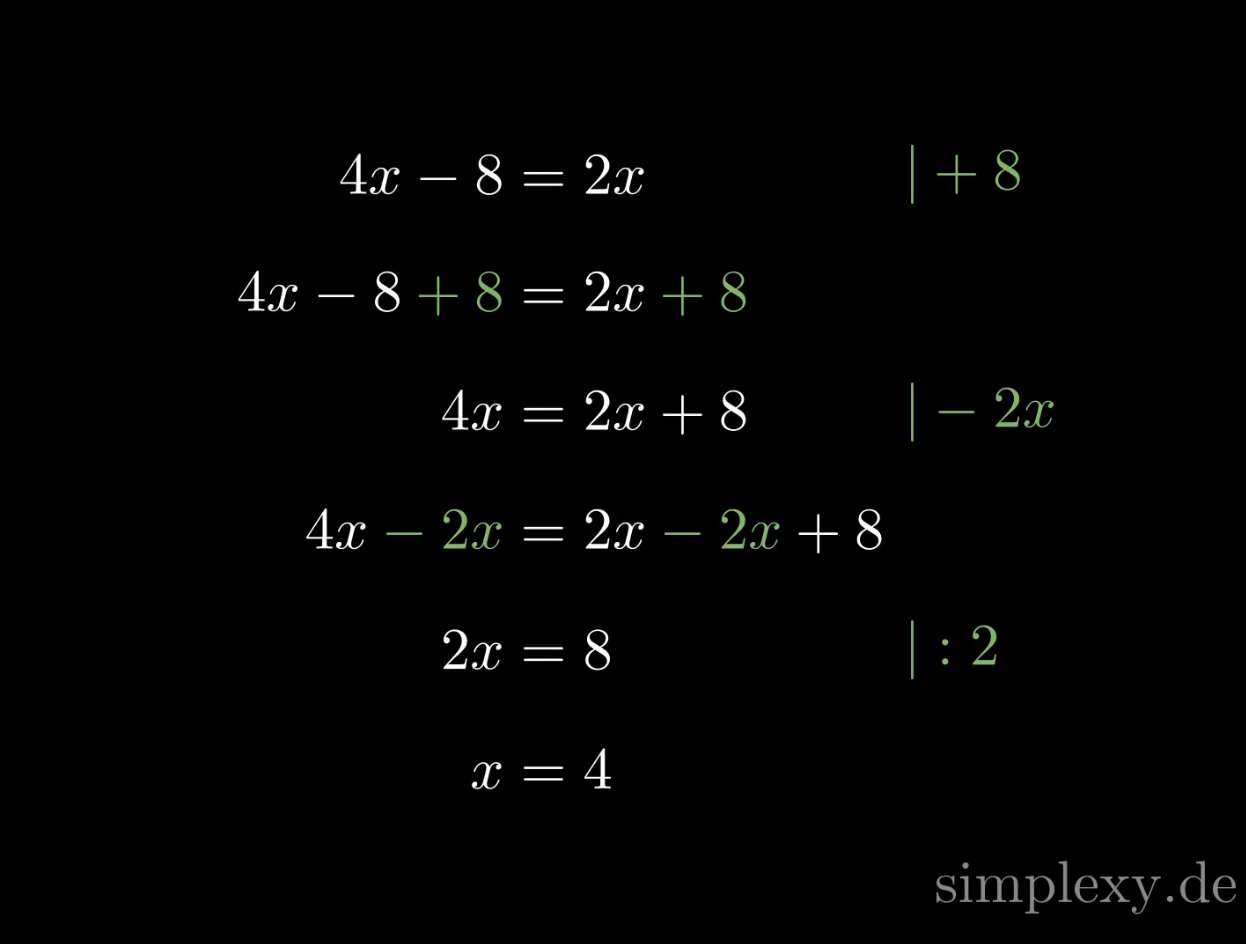
Betrachten wir jetzt mal eine Gleichung die etwas schwerer ist.
\(\begin{aligned} 3y+4\cdot (y+2)&=15\\ \\ 3y+4\cdot y+4\cdot 2&=15\\ \\ 7y+8&=15\\ \\ 7y+8&=15\,\,\,\,\,|-8\\ \\ 7y+8-8&=15-8\\ \\ 7y&=7\\ \\ 7y&=7\,\,\,\,\,|:7\\ \\ \frac{7y}{7}&=\frac{7}{7}\\ \\ y&=1\\ \end{aligned}\)
Hat man die Lösung einer Gleichung ermittelt, so ist immer gut eine Probe durchzuführen. Dazu setzt man die Lösung der Gleichung in die Gleichung ein und überprüft ob die Gleichung erfüllt ist.
In diesem Fall würde man \(y=1\) in die Gleichung
\(3y+4\cdot (y+2)=15\)
einsetzen. Damit erhält man:
\(\color{blue}\begin{aligned} 3\cdot 1+4\cdot (1+2)&=15\\ \\ 15&=15\\ \end{aligned}\)
Dadurch das wir \(15=15\) erhalten, steht auf beiden Seiten der Gleichung nachdem wir die Variable eingesetzt haben das gleiche. Die Gleichung ist damit gelöst.
Es lohnt sich immer, nachdem man die Lösung einer Gleichung berechnet hat, eine Probe durchzuführen.
Sicherlich ist dir an diesem Beispiel aufgefallen, dass die Variable nicht \(x\) sondern \(y\) ist. An der Lösungsmethode hat sich dadurch nichts verändert. Die Variable ist lediglich ein Platzhalter. Es ist vollkommen egal ob die Variable \(x\) oder \(y\) heißt.
Man solch sich nicht davon verwirren lassen, welche Variable in einer Gleichung steht. Die Variable ist nur ein Platzhalter. An der Lösungsmethode ändert sich wegen der Variable nicht.
Solche Gleichungen kannst du mit Rechner für Gleichungen lösen. Dort kannst du solche Gleichungen eingeben und lösen lassen. Bei einigen Gleichungen kannst du dir auch den Lösungsweg ansehen.
Beispiel Gleichungen mit Wurzel lösen
\(\begin{aligned} 2x^2-8&=0\\ \\ 2x^2-8&=0\,\,\,\,\,|+8\\ \\ 2x^2-8+8&=0+8\\ \\ 2x^2&=8\\ \\ 2x^2&=8\,\,\,\,\,|:2\\ \\ \frac{2}{2}x^2&=\frac{8}{2}\\ \\ x^2&=4\\ \\ x^2&=4\,\,\,\,\,|\sqrt{\,}\\ \\ \sqrt{x^2}&=\sqrt{4}\\ \\ x_1=2 \,\,\,&\land \,\,\, x_2=-2 \end{aligned}\)
Beim Gleichunen lösen die ein Quadrat bei der Variable besitzen (hier \(x^2\)) kann es vorkommen, dass man zwei Lösungen erhält. In diesem Beispiel gibt es die Lösung \(x_1=2\) und \(x_2=-2\).
Gleichungen mit Wurzel lösen
Die Gleichung \(x^2=a\) hat für den Fall
\(a>0\) die Lösungen \(x=\pm\sqrt{a}\)
\(a=0\) die Lösung \(x=0\)
\(a< 0\) Keine Lösung, denn eine Wurzel von einer negativen Zahl ist nicht definiert.
Gleichungen Lösen mit zwei "\(x\)"
\(2x+3=5x-6\)
Beim Gleichungen lösen die sowohl auf der linken als auch auf der rechten Seite ein \(x\) besitzen, muss man sich überlegen, auf welche Seite man das \(x\) sammeln möchte und auf welche Seite später die Zahlen stehen sollen.
Wir werden uns hier dafür entscheiden, die Variable \(x\) auf die linke Seite zu bringen und die Zahlen alle auf die rechte Seite. Wir können also nun die \(5x\) von der rechten Seite auf die linke Seite bringen, indem wir auf beiden Seiten der Gleichung \(-5x\) rechnen.
\(\begin{aligned} 2x+3&=5x-6\,\,\,\,\,|-5x\\ 2x+3-5x&=5x-5x-6\\ -3x+3&=-6\\ \end{aligned}\)
Als nächstes können wir die \(3\) von der linken Seite auf die rechte Seite bringen.
\(\begin{aligned} -3x+3&=-6\,\,\,\,\,|-3\\ -3x+3-3&=-6-3\\ -3x&=-9\\ \end{aligned}\)
Nun können wir die \(-3\) die vor dem \(x\) steht beseitigen indem wir die Gleichung durch \(-3\) teilen.
\(\begin{aligned} -3x&=-9\,\,\,\,\,|:(-3)\\ \\ \frac{-3x}{-3}&=\frac{-9}{-3}\\ \\ x&=3 \end{aligned}\)
Die lösung der Gleichung ist \(x=3\).
Stehen auf beiden Seiten der Gleichung eine Variable, so muss man sich zunächst entscheiden, auf welche Seite man die Variablen sammeln möchte und auf welche Seite die Zahlen gesammelt werden.
Gleichungen lösen mit Klammern
Nun möchten wir Gleichungen lösen in denen Klammern vorkommen.
Wir betrachten die Gleichung
\(2\big(x+3\big)=10\)
Besitzt eine Gleichung zu Beginn Klammern, so muss man diese zuerst auflösen.
Hier müssen wir also die \(2\) in die Klammer ziehen bzw. die \(2\) mit jedem Term in der Klammer multiplizieren.
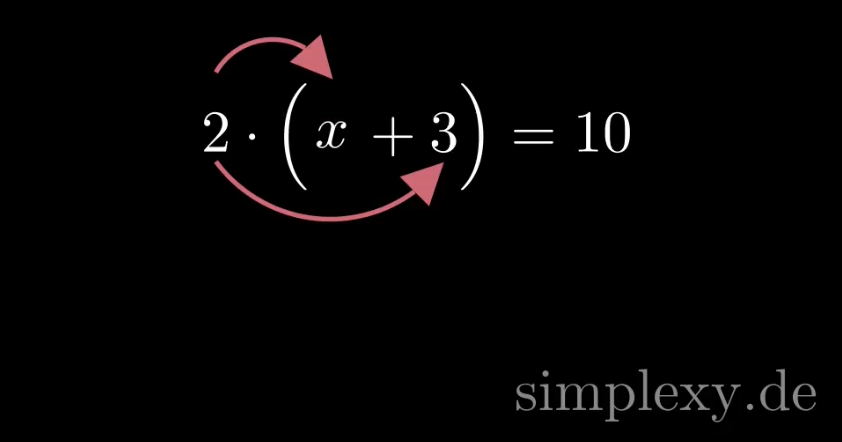
Wir erhalten dann:
\(2x+6=10\)
Ab hier kann man die Gleichung wie gewohnt lösen...
\(\begin{aligned} 2x+6&=10\,\,\,\,\,|-6\\ \\ 2x&=4\\ \\ x&=2 \end{aligned}\)
Als lösung der Gleichung erhalten wir damit \(x=2\).
Klammern in der Gleichung
Gleichungen mit Klammern lösen funktioniert genauso wie das Lösen einer Gleichung ohne Klammern. Man allerdings zuerst die Klammern ausmultipliziert.
Gleichungen lösen mit zwei Klammern
Bei Gleichungen mit Klammern kann es vorkommen, dass zwei klammern vorhanden sind. In so einem Fall muss man beide Klammern ausmultiplizieren.
\(2x-\big(3x+5\big)=3\big(x+3\big)\)
Auf der linken Seite der Gleichung steht vor der Klammer ein Minus. Ein Minus vor der Klammer sorgt dafür, dass sich die Vorzeichen in der Klammer umkehren. Auf der rechten Seite wird die Klammer wie gewohnt ausmultipliziert.
\(2x-3x-5=3x+9\)
Nun können die die Gleichung lösen...
Wir fassen dazu auf der linken Seite \(2x-3x\) zu \(-1x\) zusammen.
\(\begin{aligned} -1x-5&=3x+9\\ -1x-5&=3x+9\,\,\,\,\,|+5\\ -1x&=3x+14\\ -1x&=3x+14\,\,\,\,\,|-3x\\ -1x-3x&=14\\ -4x&=14\\ \end{aligned}\)
Jetzt müssen wir die \(-4\) vor dem \(x\) eleminieren. Das tun wir wieder indem wir die gesammte Gleichung durch \(-4\) teilen.
\(\begin{aligned} -4x&=14\,\,\,\,\,|:(-4)\\ \\ \frac{-4x}{-4}&=\frac{14}{-4}\\ \\ x&=-\frac{14}{4} \end{aligned}\)
Als Lösung der Gleichung erhalten wir damit \(x=\) \(-\frac{14}{4}\)
Gleichungen mit zwei Klammern lassen sich genauso lösen wie Gleichungen mit einer Klammer. Man muss als Erstes die Klammern ausmultiplizieren und anschießend die Gleichungen wie gewohnt lösen.
Bruchgleichungen lösen
Gleichungen lösen in denen Brüche vorkommen ist nicht schwer. Am besten man geht so vor wie in dem nächsten Beispiel gezeigt.
\(\begin{aligned} \frac{2x+2}{3}&=\frac{x-3}{2} \end{aligned}\)
Hier muss man zuerst die Nenner auf beiden Seiten der Gleichung eliminieren. Das machen wir, indem wir die Gleichung mit den Nennern multiplizieren. So verschwindet auf beiden Seiten der Bruch und wir können die Gleichung lösen indem wir wie gewohnt weiter machen.
\(\begin{aligned} \frac{2x+2}{3}&=\frac{x-3}{2}\,\,\,\,\,|\cdot 2\\ \\ \frac{2\cdot (2x+2)}{3}&=\frac{2\cdot(x-3)}{2}\\ \\ \frac{4x+4}{3}&=x-3\,\,\,\,\,|\cdot 3\\ \\ \frac{3\cdot (4x+4)}{3}&=3\cdot(x-3)\\ \\ 4x+4&=3x-9\,\,\,\,\,|-3x\\ \\ x+4&=-9\,\,\,\,\,|-4\\ \\ x&=-13\\ \end{aligned}\)
Die Lösung der Gleichung lautet also \(x=-13\).
Gleichungen lösen mit Klammern und Bruch
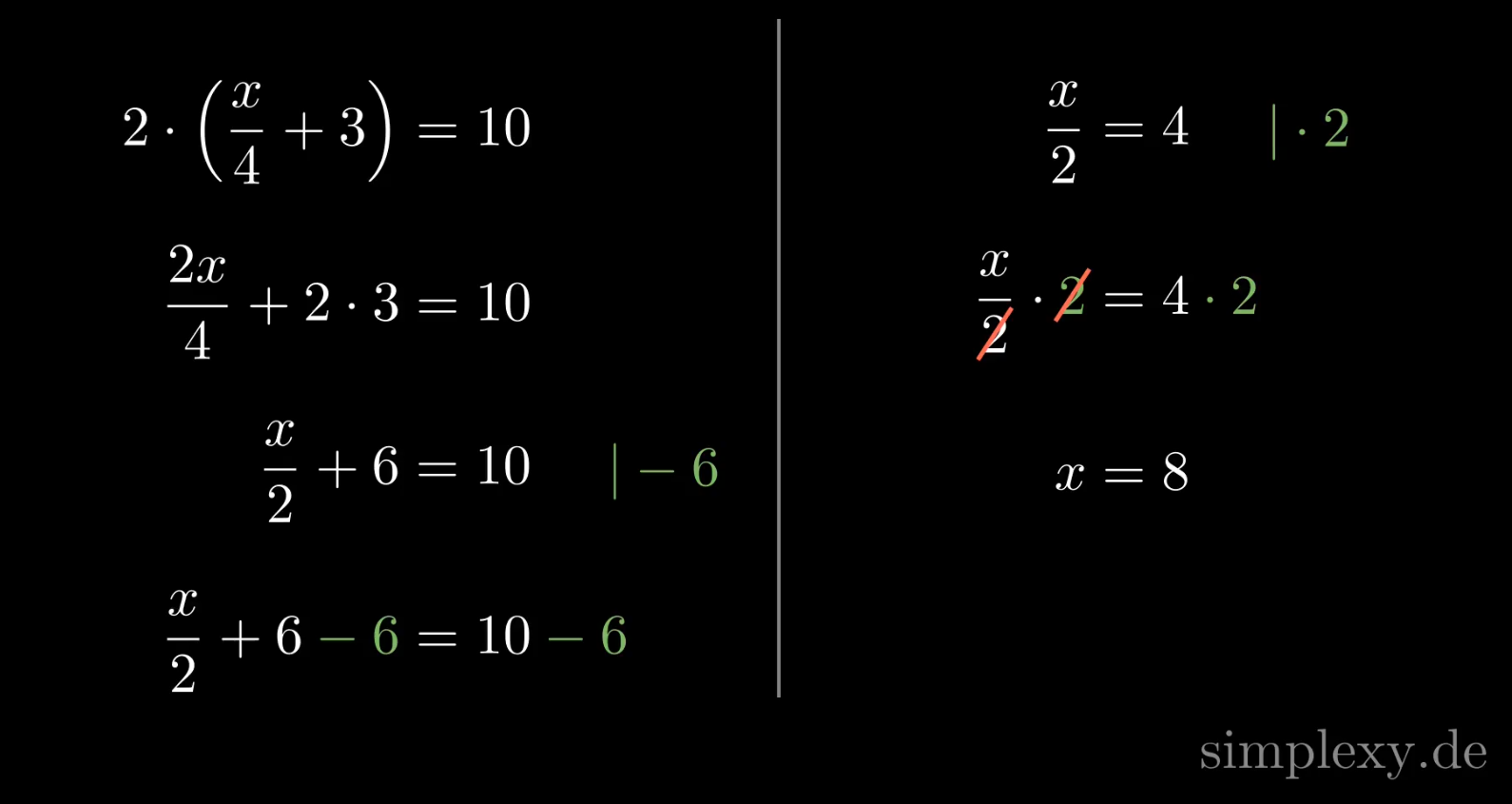
Gleichungen Lösen in denen das \(x\) im Nenner steht.
Wenn man eine Gleichung lösen muss, indem die Variable (hier \(x\)) im Nenner steht, so kann ein Trick besonders hilfreich sein.
\(\begin{aligned} \frac{2}{x}&=\frac{1}{4}\\ \end{aligned}\)
Man kann auf beiden Seiten der Gleichung den Kehrwert bilden, so wird das \(x\) aus dem Nenner in den Zähler gebracht. Um den Kehrwert zu bilden muss alles was im Nenner steht in den Zähler geschrieben werden und alles was im Zähler steht muss in den Nenner geschrieben werden.
\(\begin{aligned} \frac{2}{x}&=\frac{1}{4}\,\,\,\,\,|\text{Kehrwert}\\ \\ \frac{x}{2}&=\frac{4}{1}\\ \\ \frac{x}{2}&=4\,\,\,\,\,|\cdot 2\\ \\ x&=8 \end{aligned}\)
Die Lösung der Gleichung lautet \(x=8\).
Variable einer Gleichung ausklammern
Gleichungen mit Klammern können manchmal gelöst werden, indem man die Variable ausklammert
\(x^3-\frac{1}{4}x^4=0\)
Diese Gleichung lösen können wir, indem wir das größte gemeinsame \(x\) ausklammern, das geht wie folgt:
\(\begin{aligned} x^3-\frac{1}{4}x^4&=0\,\,\,\,\,|x^3\text{ausklammern}\\ \\ x^3\Big(1-\frac{1}{4}x\Big)&=0 \end{aligned}\)
Wir haben nun unsere Gleichung umgewandelt und können den Satz vom Nullprodukt anwenden.
Ein Produkt ist genau dann Null, wenn einer der beiden Faktoren Null ist.
\(\underbrace{\underbrace{x^3}_{Faktor}\underbrace{\Big(1-\frac{1}{4}x\Big)}_{Faktor}}_{Produkt}=0\)
Nach dem Ausklammern von \(x^3\) können wir nun für jeden Faktor eine eigne Gleichung erstellen. Denn nach dem Satz vom Nullprodukt muss gelten:
\(\begin{aligned} x^3=0\,\,&\text{oder}\,\,1-\frac{1}{4}x=0\\ \\ &\implies\\ \\ x_1=0\,\,&\text{oder}\,\,x_2=4 \end{aligned}\)
Als Lösung haben wir damit \(x_1=0\) und \(x_2=4\).
Es lohnt sich diese Lösungsmethode anzuwenden, wenn in jedem Faktor der Ausgangsgleichung ein \(x\) vorkommt.
pq-Formel
Um quadratische Gleichungen lösen zu können benötigt man die pq-Formel oder Mitternachtsformel. Manchmal wird die Mitternachtsformel auch abc-Formel genannt.
Eine quadratische Gleichung hat die Form
\(x^2+px+q=0\)
Man erhält die Lösung dieser Gleichung mit der pq-Formel.
pq-Formel
\(x_{1/2}=\)\(-\frac{p}{2}\pm\sqrt{(\frac{p}{2})^2-q}\)
Fallunterscheidung:
\(x_{1}=\)\(-\frac{p}{2}-\sqrt{(\frac{p}{2})^2-q}\)
\(x_{1}=\)\(-\frac{p}{2}+\sqrt{(\frac{p}{2})^2-q}\)
Die pq-Formel kann bis zu zwei Lösungen besitzen. Es kann also vorkommen das eine quadratische Gleichung keine, eine oder zwei Lösungen besitzt. Um die Anzahl an Lösungen zu bekommen, muss man die sogenannte Diskriminante ausrechnen.
\(D=(\frac{p}{2})^2-q\)
Die Diskriminante ist der Term unter der Wurzel in der pq-Formel. Es gilt:
Regel:
Die Anzahl an Lösungen erhältst du über die Diskriminante D
- Wenn \(D\) kleiner als null ist, dann existieren keine Lösung.
- Wenn \(D=0\) ist, dann existiert genau eine Lösung.
- Wenn \(D\) größer als null ist, dann existieren zwei Lösungen.
\(D=(\frac{p}{2})^2-q\)
Beispiel 1:
\(x^2-6x-7=0\)
Wir können direkt \(p\) und \(q\) ablesen.
\(p=-6\) und \(q=-7\)
Nun müssen wir \(p\) und \(q\) in die pq-Formel einsetzen.
\(\begin{aligned} x_{1/2}&=-\frac{p}{2}\pm\sqrt{\Big(\frac{p}{2}\Big)^2-q}\\ \\ &=-\frac{-6}{2}\pm\sqrt{\Big(\frac{-6}{2}\Big)^2-(-7)}\\ \\ &=3\pm\sqrt{9+7}\\ \\ &=3\pm\sqrt{16}\\ \end{aligned}\)
Fallunterscheidung:
\(x_{1}=3-\sqrt{16}=-1\)
\(x_{2}=3+\sqrt{16}=7\)
Beispiel 2:
\(x^2-4x+4=0\)
Wir bestimmen wieder \(p\) und \(q\).
\(p=-4\) und \(q=4\)
Nun können wir \(p\) und \(q\) wieder in unsere pq-Formel einsetzen und wie gewohnt die Gleichung lösen...
\(\begin{aligned} x_{1/2}&=-\frac{p}{2}\pm\sqrt{\Big(\frac{p}{2}\Big)^2-q}\\ \\ &=-\frac{-4}{2}\pm\sqrt{\Big(\frac{-4}{2}\Big)^2-4}\\ \\ &=2\pm\sqrt{4-4}\\ \\ &=2\pm\textcolor{blue}{\sqrt{0}}\\ \end{aligned}\)
Diese Gleichung hat also nur eine einzige Lösung bei \(x_0=2\). Über die Diskriminante kann man berechnen wie viele Nullstellen die Gleichung besitzt. Indiesem Fall hat die Diskriminante den Wert Null:
\(D=\Big(\frac{p}{2}\Big)^2-q=4-4=0\)
Nun haben wir also auch gezeigt, dass diese Gleichung nur eine einzige Lösung besitzt.
Beispiel 3:
\(x^2-4x+10=0\)
Wir lesen \(p\) und \(q\) wieder aus der Gleichung ab.
\(p=-4,\) \(q=10\)
Nun setzen wir \(p\) und \(q\) in die pq-Formel ein.
\(\begin{aligned} x_{1/2}&=-\frac{p}{2}\pm\sqrt{\Big(\frac{p}{2}\Big)^2-q}\\ \\ &=-\frac{-4}{2}\pm\sqrt{\Big(\frac{-4}{2}\Big)^2-10}\\ \\ &=2\pm\sqrt{4-10}\\ \\ &=2\pm\textcolor{red}{\sqrt{-6}}\\ \end{aligned}\)
In diesem Beispiel hat die quadratische Gleichung keine Nullstelle. Die Wurzel einer negativen Zahl ist nicht definiert. Aus diesem Grund hat diese quadratische Gleichung keine Lösungen.
Mitternachtsformel bzw. ABC Formel
Eine Gleichung der Form
\(ax^2+bx+c=0\)
kann mit Hilfe der Mitternachtsformel gelöst werden.
Mitternachtsformel
\(x_{1/2}=\)\(\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
Fallunterscheidung:
\(x_{1}=\)\(\frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(x_{2}=\)\(\frac{-b+\sqrt{b^2-4ac}}{2a}\)
Die Mitternachtsformel-Formel liefert zwei Lösungen \(x_{1/2}\), denn eine quadratische Gleichung kann bis zu zwei Lösungen bestizen. Entwieder man hat keine, eine oder zwei Lösungen. Um die Anzahl an Lösungen zu berechnen, kann man die Diskriminante betrachten.
\(D=b^2-4ac\)
Die Diskriminante ist der Term unter der Wurzel in der Mitternachts-Formel. Es gilt:
Regel:
Über die Diskriminante erhält man die Anzahl an Lösungen
- Wenn \(D < 0\) ist, dann existieren keine Lösung.
- Wenn \(D=0\) ist, dann existiert genau eine Lösung.
- Wenn \(D>0\) ist, dann existieren zwei Lösungen.
Beispiel 1:
\(2x^2-12x-14=0\)
Wir können die werte \(a,b\) und \(c\) aus der Gleichung ablesen.
\(a=2,\) \(b=-12\) und \(c=-14\)
Diese Werte setzen wir in die Mitternachtsformel ein.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-(-12)\pm\sqrt{(-12)^2-4\cdot 2\cdot (-14)}}{2\cdot 2}\\ \\ &=\frac{12\pm\sqrt{144+112}}{4}\\ \\ &=\frac{12\pm\sqrt{256}}{4}\\ \\ &=\frac{12\pm 16}{4}\\ \end{aligned}\)
Fallunterscheidung:
\(x_{1}=\)\(\frac{12-16}{4}\)\(=-1\)
\(x_{2}=\)\(\frac{12+16}{4}\)\(=7\)
Diese Gleichung besitzt zwei Lösungen
\(x_1=-1\) und \(x_2=7\)
Beispiel 2:
\(4x^2-16x+16=0\)
Auch hier können wir wieder \(a,b\) und \(c\) ablesen.
\(a=4,\) \(b=-16\) und \(c=16\)
Nun können wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-(-16)\pm\sqrt{(-16)^2-4\cdot 4\cdot 16}}{2\cdot 4}\\ \\ &=\frac{16\pm\sqrt{256-256}}{8}\\ \\ &=\frac{16\pm\textcolor{blue}{\sqrt{0}}}{8}\\ \\ &=\frac{16\pm 0}{8}\\ \\ &=\frac{16}{8}\\ \\ &=2\\ \end{aligned}\)
In diesem Beispiel hat die quadratische Gleichung nur eine Lösung, da
die Diskriminante \(D\) gleich Null ist.
\(D=b^2-4ac=0\)
Die einzige Lösungen lautet
\(x_0=2\)
Beispiel 3:
\(2x^2-8x+11=0\)
Wir lesen \(a,b\) und \(c\) wieder ab und erhalten
\(a=2,\) \(b=-8\) und \(c=11\)
Nun setzen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ &=\frac{-(-8)\pm\sqrt{(-8)^2-4\cdot 2\cdot 11}}{2\cdot 2}\\ &=\frac{8\pm\sqrt{64-88}}{4}\\ &=\frac{16\pm\textcolor{red}{\sqrt{-24}}}{4}\\ \end{aligned}\)
Da wir die Wurzel einer negativen Zahl nicht berechnen können, besitzt diese Gleichung keine Lösung.
Gleichungen mit \(e\)-Funktion lösen
Man kann Gleichungen lösen in denen die \(e\)-Funktion vorkommt, wenn man die Umkehrfunktion der \(e\)-Funktion verwendet.
Die Umkehrfunktion der \(e\)-Funktion ist der natürliche Logarithmus.
Die folgenden Beziehungen sind hlfreich, wenn man Gleichungen mit \(e\)-Funktion lösen möchte.
\(\begin{aligned} e^{ln(x)}&=x\\ &\text{bzw.}\\ ln(e^x)&=x \end{aligned}\)
Beispiel 1:
\(e^{2x}=0\)
\(\begin{aligned} e^{2x}&=0\,\,\,\,\,|ln(...)\\ \\ ln(e^{2x})&=ln(0)\\ \\ 2x&=\color{red}{ln(0)} \end{aligned}\)
Hier müssen wir aufhören zu rechnen den der \(ln(0)\) ist nicht definiert. Diese Gleichung besitzt also keine Lösung.
Beispiel 2:
\(4e^{-2x}-16=0\)
Wir werden zuerst dafür sorgen, dass der Term \(e^{-2x}\) alleine auf der linken Seite steht. Im Anschluss werden wir den \(ln()\) verwenden um den exponenten \(-2x\) nach unten zu bringen...
\(\begin{aligned} 4e^{-2x}-16&=0\,\,\,\,\,|+16\\ \\ 4e^{-2x}&=16\,\,\,\,\,|:4\\ \\ e^{-2x}&=4\,\,\,\,\,|ln(...)\\ \\ ln(e^{-2x})&=ln(4)\\ \\ -2x&=ln(4)\,\,\,\,\,|:(-2)\\ \\ x&=-\frac{ln(4)}{2} \end{aligned}\)
Die Lösung der Gleichung lautet:
\(x=-\)\(\frac{ln(4)}{2}\)
Beispiel 3:
\(\begin{aligned} 4e^{-3x}-e^{2x}&=0\,\,\,\,\,|+e^{2x}\\ \\ 4e^{-3x}&=e^{2x}\,\,\,\,\,|ln(...)\\ \\ ln(4e^{-3x})&=ln(e^{2x})\\ \\ ln(4)+ln(e^{-3x})&=2x\\ \\ ln(4)-3x&=2x\,\,\,\,\,|-ln(4)\\ \\ -3x&=2x-ln(4)\,\,\,\,\,|-2x\\ \\ -5x&=-ln(4)\,\,\,\,\,|:(-5)\\ \\ x&=\frac{ln(4)}{5}\\ \end{aligned}\)
Die Lösung der Gleichung lautet:
\(x=\)\(\frac{ln(4)}{5}\)
