Elektrische Leistung
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Elektrische Leistung
Strom ist aus dem heutigen Leben nicht mehr weg zu denken, er ist eines der wichtigsten Energiequellen. Das besondere an Strom als Energieträger ist seine Transportierbarkeit.
In diesem Kapitell werden wir uns mit der elektrischen Leistung befassen, sie gibt an wie viel elektrische arbeit in einem Zeitintervall verrichtet wird. Im Folgenden werden wir uns mit der Berechnung der elektrische Leistung befassen und einige praktische Beispiele berechnen.
Bevor wir uns dem Thema widmen, könnte es nützlich sein die folgenden Themen zu wiederholen:
Elektrische Leistung erklärt
Die elektrische Leistung gibt an wie viel elektrische Arbeit \(W\) in einem bestimmten Zeitintervall verrichtet wird bzw. wie viel elektrische Energie in einem Zeitintervall umgesetzt wird. Um die elektrische Leistung berechnen zu können, muss folgende Formel verwenden:
\(\begin{aligned} P=\frac{W}{t} \end{aligned}\)
Mit der elektrischen Leistung kann demzufolge angeben wie hoch der Energieverbrauch bzw. der Energiebedarf eines elektrischen Bauteils ist.
Elektrische Leistung Formel
Die Definition der Leistung als "verrichtete Arbeit pro Zeit" bezieht sich nicht nur auf die Elektrizitätslehre. Es handelt sich dabei um eine allgemeine Definition der Leistung in der Physik. Die Formel
\(\begin{aligned} P=\frac{W}{t} \end{aligned}\)
ist eine allgemeingültige Formel. Setzt man für die Arbeit \(W\) die elektrische Arbeit \(W=U\cdot q\) ein, so gelangt man zur Formel der elektrischen Leistung.
\(\begin{aligned} P&=\frac{W}{t}\\ \\ &=\frac{U\cdot q}{t}\\ \end{aligned}\)
Nun kann man noch die Definition der Stromstärke
\(\begin{aligned} I=\frac{q}{t} \end{aligned}\)
verwenden. Diese Formel kann nach \(q\) umgestellt werden.
\(\begin{aligned} q=I\cdot t \end{aligned}\)
Dieser Ausdruck für die Ladung \(q\) kann nun in die Formel für die Leisung \(P\) eingesetzt werden.
\(\begin{aligned} P&=\frac{U\cdot q}{t}\\ \\ &=\frac{U\cdot I\cdot \bcancel{t}}{\bcancel{t}}\\ \\ &=U\cdot I \end{aligned}\)
Man kann die elektrische Leistung berechnen, über das Produkt aus Spannung \(U\) und Stromstärke \(I\).
Elektrische Leistung Formel
\(\begin{aligned} P=U\cdot I \end{aligned}\)
Dabei ist:
\(P\) die elektrische Leistung in Watt \([W]\)
\(U\) die Spannung in Volt \([V]\)
\(I\) die Stromstärke in Ampere \([A]\)
Elektrische Leistung berechnen Beispiel
Eine Glühbirne wird bei einer Spannung von \(12\) Volt und einer Stromstärke von \(2\) Ampere betrieben. Damit ist die Leistung: \(P=U\cdot I=12V\cdot 2A=24W\). Die Lampe wandelt also 24 Watt elektrische Energie in Lichtenergie und Wärme um.
Die Formel \(P=U\cdot I\) ist nur für konstante Stromstärken und Spannungen anwendbar.
Elektrische Leistung Einheit
Die Einheit der elektrischen Leistung ist Watt
\([P]=W \text{ (Watt)}\)
In der Elektrizitätslehre hat man es oft mit sehr kleinen bis hin zu sehr großen elektrischen Leistungen zu tun.
| Mikrowatt \(\mu W\) | \(1\cdot 10^{-6}W\) |
| Milliwatt \(m W\) | \(1\cdot 10^{-3}W\) |
| Kilowattt \(k W\) | \(1\cdot 10^{3}W\) |
| Megawatt \(M W\) | \(1\cdot 10^{6}W\) |
Die Einheiten kannst du wie folgt umrechnen:
\(\begin{aligned} 1W&=1000mW\\ \\ 1mW&=1000\mu W\\ \\ 1MW&=1000kW\\ \\ 1kW&=1000W\\ \\ \end{aligned}\)
Weitere Formeln
Wie wir bis jetzt wissen, kann die elektrische Leistung als Produkt der Spannung \(U\) und dem Strom \(I\) berechnet werden. Diese zwei Größen hängen jedoch über das Ohmsche Gesetz zusammen.
So kann man beispielsweise die Formel
\(\begin{aligned} U=R\cdot I \end{aligned}\)
verwenden, um die folgende Formel für die elektrische Leistung zu erhalten:
\(P=U\cdot I=R\cdot I\cdot I=R\cdot I^2\)
\(P=R\cdot I^2\)
Dabei ist:
\(P\) die elektrische Leistung in Watt \([W]\)
\(R\) der Widerstand in Ohm \([\Omega]\)
\(I\) die Stromstärke in Ampere \([A]\)
Um eine weitere Formel der elektrischen Leistung zu erhalten, nutzen wir das Ohmsche Gesetz in der Form
\(\begin{aligned} I=\frac{U}{R} \end{aligned}\)
Damit erhalten wir für die elektrische Leistung:
\(\begin{aligned} P=U\cdot I=U\cdot\frac{U}{R}=\frac{U^2}{R} \end{aligned}\)
\(\begin{aligned} P=\frac{U^2}{R} \end{aligned}\)
Dabei ist:
\(P\) die elektrische Leistung in Watt \([W]\)
\(R\) der Widerstand in Ohm \([\Omega]\)
\(U\) die Spannung in Volt \([V]\)
Die elektrische Leistung kann über verschiedene Formeln berechnet werden. Je nach Aufgabenstellung muss man entscheiden welche Formel Anwendung findet.

Elektrische Leistung Berechnen
Nun folgen zwei Beispiele um zu zeigen, wie man die elektrische Leistung berechnen kann.
Beispiel 1
Ein Fernseher benötigt eine Betriebsspannung von \(U=230V\) und bezieht \(I=0,5A\) Strom. Wie groß ist die aufgenommene elektrische Leistung?

Um die aufgenommene elektrische Leistung berechnen zu können, verwenden wir die Formel
\(\begin{aligned} P=U\cdot I \end{aligned}\)
Dort setzen wir nun \(U=230V\) und \(I=0,5A\) ein und erhalten:
\(\begin{aligned} P=230V\cdot 0,5A=115W \end{aligned}\)
Der Fernseher hat eine Leistung von \(115\) Watt aufgenommen.
Beispiel 2
Ein \(500\Omega\) Widerstand verträgt eine Maximalleistung von \(10\) Watt. Wie groß ist die Maximalspannung, welche an den Widerstand angeschlossen sein darf?
Um die Maximalspannung berechnen zu können, welche an dem Widerstand anliegen darf, verwenden wir die Formel:
\(\begin{aligned} P=\frac{U^2}{R} \end{aligned}\)
Diese Formel muss nach der Spannung \(U\) umgestellt werden:
\(\begin{aligned} U_{max}&=\sqrt{P_{max}\cdot R}\\ \\ &=\sqrt{10W\cdot 500\Omega}\\ \\ &=70,71V \end{aligned}\)
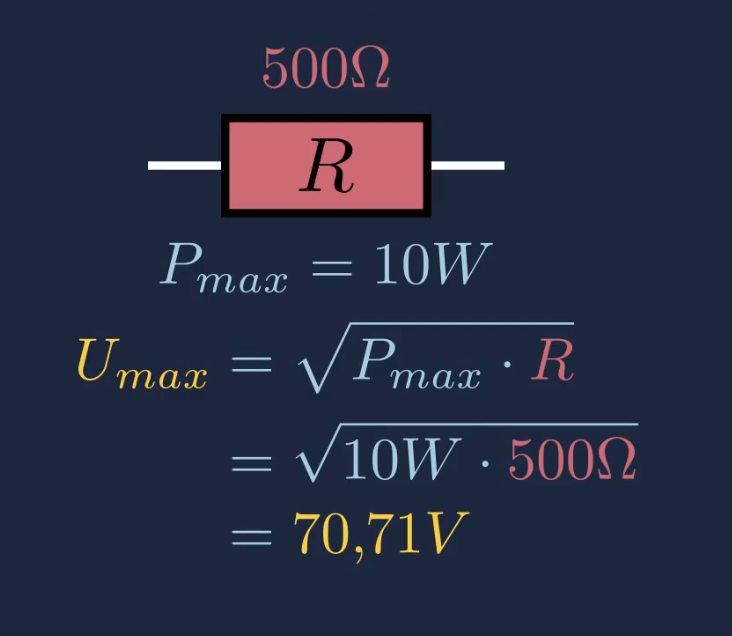
Die Maximalspannung welche an dem Widerstand anliegen darf beträgt \(70,71V\).
