Fadenpendel Beschleunigung
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Fadenpendel Zusammenfassung
Die Schwingungsgleichung vom Fadenpendel kann über die Betrachtung der Rückstellkraft ermittelt werden. Dabei ist die Rückstellkraft gerade die Tangentialkomponente der Gewichtskraft.
Die Schwingungsgleichung vom Fadenpendel lautet:
\(\begin{aligned} \ddot{x}(t)+\frac{g}{l}\cdot x(t)=0 \end{aligned}\)
Dabei ist:
\(x(t)\) die Auslenkung.
\(l\) die Länge des Fadens.
\(g\) die Fallbeschleunigung.
Das Fadenpendel schwingt harmonisch mit der Ort-Zeit-Funktion
\(x(t)=x_0\cdot cos(\omega\cdot t)\)
Dabei ist \(\omega\) die Eigenfrequenz bzw. Kreisfrequenz des Pendels.
\(x_0\) ist die Startauslenkung des Pendels.
\(\begin{aligned} \omega=\sqrt{\frac{g}{l}} \end{aligned}\)
Die Schwingungsdauer bzw. die Periodendauer berechnet sich über
Die Frequenz berechnet sich über
\(\begin{aligned} T=\frac{2\pi}{\omega} \end{aligned}\)
\(\begin{aligned} T=2\pi\cdot\sqrt{\frac{l}{g}} \end{aligned}\)
\(\begin{aligned} f=\frac{1}{T} \end{aligned}\)
Fadenpendel Beschleunigung
In dem unteren Video ist die Beschleunigung vom Fadenpendel leicht erklärt.
In dem Beitrag über die Schwingungsgleichung des Fadenpendels haben wir die Ort-Zeit-Funktion des Pendels berechnet. Dort haben wir rausgefunden, dass sich das Pendel harmonisch mit der Ort-Zeit-Funktion
\(x(t)=x_0\cdot cos(\omega\cdot t)\)
bewegt. Dabei ist \(\omega\) die Eigenfrequenz bzw. Kreisfrequenz des Pendels.
\(\begin{aligned} \omega=\sqrt{\frac{g}{l}} \end{aligned}\)
\(x_0\) ist die Startauslenkung (Amplitude) der Schwingung.
Sobald das Fadenpendel losgelassen wird, beschleunigt es sich in Richtung der Ruhelage. Aufgrund der Trägheit fliegt der Pendelkörper durch die Ruhelage hindurch und gelangt zum anderen Umkehrpunkt. Dort kommt das Pendel für einen kurzen Moment zum Stillstand, und wird anschließend wieder in Richtung der Ruhelage beschleunigt.
Beim Durchgang durch die Ruhelage ist die Geschwindigkeit des Pendels maximal und an den Umkehrpunkten ist die Geschwindigkeit Null \((v=0)\).
Um den zeitlichen Verlauf der Geschwindigkeit und der Beschleunigung zu erhalten können wir die Ort-Zeit-Funktion \(x(t)\) nach der Zeit ableiten.
Geschwindigkeit
\(v=\)\(\frac{\Delta x}{\Delta t}\)
bzw.
\(v=\dot{x}=\)\(\frac{dx}{dt}\)
Beschleunigung
\(a=\)\(\frac{\Delta v}{\Delta t}\)
bzw.
\(a=\dot{v}=\ddot{x}=\)\(\frac{d^2x}{dt^2}\)
Um den zeitlichen Verlauf der Geschwindigkeit zu ermitteln müssen wir also die Ort-Zeit-Funktion des Pendels einmal nach der Zeit ableiten.
\(\dot{x}(t)=-x_0\cdot \omega\cdot sin(\omega t)\)
Geschwindigkeit vom Fadenpendel
\(v(t)=-x_0\cdot \omega\cdot sin(\omega t)\)
Hinweis:
Für die Ableitung muss man die Kettenregel anwenden.
Dafür muss man die äußeren Ableitung mit der inneren ableitung von \(cos(\omega\cdot t)\) multiplizieren.
Die äußeren Ableitung von \(cos(\omega t)\) lautet:
\(-sin(\omega\cdot t)\)
und die innere Ableitung lautet:
\(\frac{d(\omega\cdot t)}{dt}\)\(=\omega\)
Die innere Ableitung mal die äußere Ableitung liefert also:
\(v(t)=-x_0\cdot \omega\cdot sin(\omega t)\)
Um nun die Beschleunigung vom Fadenpendel zu berechnen, müssen wie die Ort-Zeit-Funktion \(x(t)\) zwei mal nach der Zeit ableiten. Da wir bereits die erste Ableitung (Geschwindigkeit) ermittelt haben, können wir nun die Geschwindigkeit einmal nach der Zeit ableiten.
Beschleunigung des Pendels
\(a(t)=\dot{v}(t)\)
\(a(t)=-x_0\cdot \omega^2\cdot cos(\omega\cdot t)\)
Wir haben auch hier die Kettenregel verwendet um die Ableitung zu berechnen.
Die äußeren Ableitung von \(-sin(\omega t)\) lautet:
\(-cos(\omega\cdot t)\)
und die innere Ableitung lautet:
\(\frac{d(\omega\cdot t)}{dt}\)\(=\omega\)
Die innere Ableitung mal die äußere Ableitung liefert also:
\(a(t)=-x_0\cdot \omega^2\cdot cos(\omega t)\)
In der folgenden Abbildung ist der zeitliche Verlauf der Beschleunigung dargestellt.
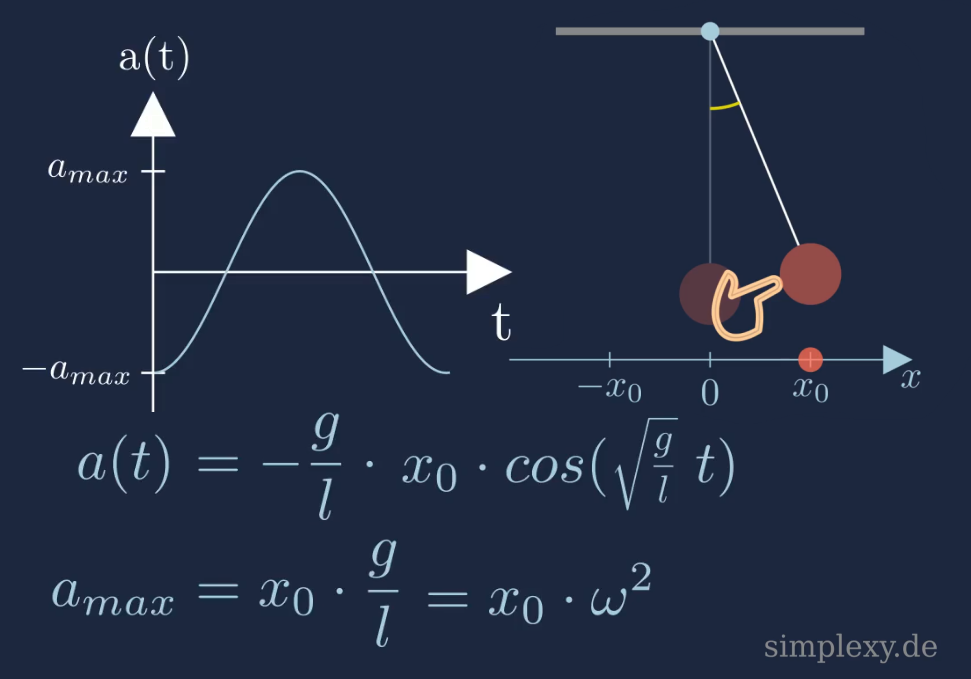
Merke
Wir haben als Ort-Zeit-Funktion \(x(t)=x_0\cdot cos(\omega\cdot t)\) verwenden, dass geht einher mit einem Fadenpendel das zum Anfangszeitpunkt nach rechts ausgelenkt ist. Betrachtet man ein Pendel das von der Ruhelage angestoßen wird, so lautet die Ort-Zeit-Funktion:
\(s(t)=x_0\cdot sin(\omega\cdot t)\)
und damit wäre die Geschwindigkeit für diesen Fall:
\(v(t)=x_0\cdot \omega\cdot cos(\omega t)\)
Und die Beschleunigung wäre:
\(a(t)=-x_0\cdot \omega^2\cdot sin(\omega t)\)
Je nach Anfangbedingung erhält man also eine unterschiedliche Ort-Zeit-Funktion. In beiden Fällen finden jedoch eine harmonische Schwingung um die Ruhelage statt, qualitativ ändert sich an der Bewegung des Pendels also nichts.
In der folgenden Abbildung ist die Ort-Zeit-Funktion, Geschwindigkeitsfunktion und die Beschleunigungsfunktion für verschiedene Anfangsbedingungen vom Fadenpendel angegeben.
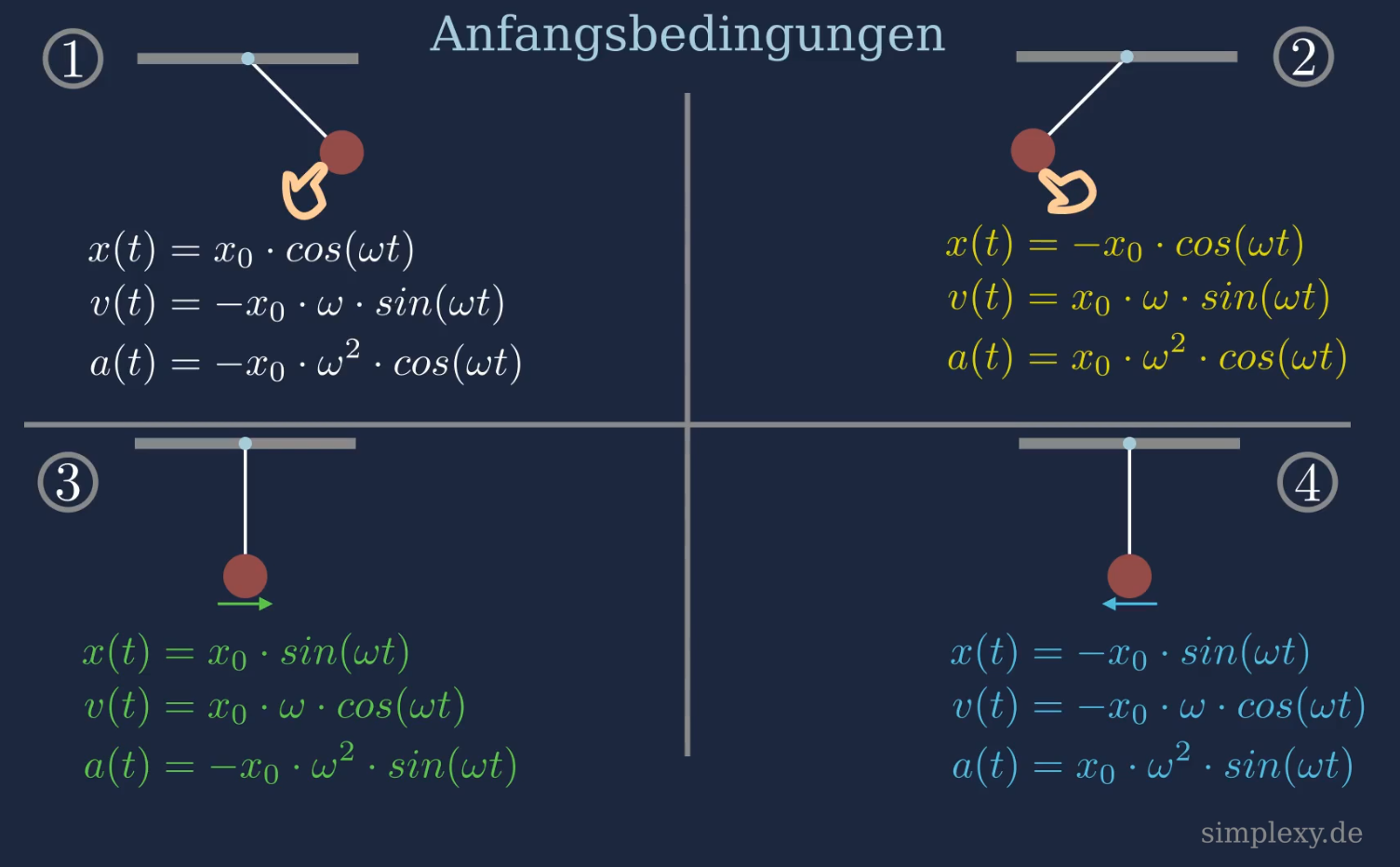
In dem folgenden Video ist die Beschleunigung vom Fadenpendel erklärt.
