Fadenpendel Schwingungsgleichung
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Fadenpendel Formel auf einem Blick
Die Schwingungsgleichung vom Fadenpendel kann über die Betrachtung der Rückstellkraft ermittelt werden. Dabei ist die Rückstellkraft gerade die Tangentialkomponente der Gewichtskraft.
Die Schwingungsgleichung vom Fadenpendel lautet:
\(\begin{aligned} \ddot{x}(t)+\frac{g}{l}\cdot x(t)=0 \end{aligned}\)
Dabei ist:
\(x(t)\) die Auslenkung.
\(l\) die Länge des Fadens.
\(g\) die Fallbeschleunigung.
Das Fadenpendel schwingt harmonisch mit der Ort-Zeit-Funktion
\(x(t)=x_0\cdot cos(\omega\cdot t)\)
Dabei ist \(\omega\) die Eigenfrequenz bzw. Kreisfrequenz des Pendels.
\(x_0\) ist die Startauslenkung des Pendels.
\(\begin{aligned} \omega=\sqrt{\frac{g}{l}} \end{aligned}\)
Die Schwingungsdauer bzw. die Periodendauer berechnet sich über
Die Frequenz berechnet sich über
\(\begin{aligned} T=\frac{2\pi}{\omega} \end{aligned}\)
\(\begin{aligned} T=2\pi\cdot\sqrt{\frac{l}{g}} \end{aligned}\)
\(\begin{aligned} f=\frac{1}{T} \end{aligned}\)
Das Fadenpendel
Ein Fadenpendel bzw. Mathematisches Pendel besteht aus einem masselosen Faden der länge \(l\), an dessen Ende ein Pendelkörper der Masse \(m\) befestigt ist.
Um die Schwingung des Pendels mathematisch beschreiben zu können, werden folgende Vereinfachungen angenommen:
-
Sowohl die Bewegung des Pendelkörpers als auch des Fadens verlaufen reibungsfrei.
-
Der Faden wird als masselos angesehen.
-
Die Masse des Pendelkörpers wird als punktförmig betrachtet.
-
Die Anfangsauslenkung \(x_0\) soll klein sein im Vergleich zur länge \(l\) des Fadens.
Fadenpendel Schwingung
Um das Fadenpendel in Schwingung zu setzen, wird das Pendel anfangs um eine kleine Strecke \(x_0\) aus der Ruhelage (Gleichgewichtslage) ausgelenkt und dann losgelassen. Daraufhin vollführt das Pendel eine harmonische Schwingung um die Ruhelage. Dabei bewegt sich das Pendel von einen Umkehrpunkt \(x_0\) zum anderen Umkehrpunkt \(-x_0\) hin und her.

Für die Beschreibung der harmonischen Schwingung vom Fadenpendel sind die folgenden Größen relevant:
-
Fadenlänge \(l\) bezieht sich auf den Abstand zwischen dem Aufhängepunkt und dem Schwerpunkt des Pendelkörpers.
-
Masse \(m\) des Pendelkörpers.
-
Fallbeschleunigung \(g\) welche mit der Masse \(m\) zusammen die Gewichtskraft ausmacht. Auf der Erde wird die Fallbeschleunigung auch Erdbeschleunigung genannt und beträgt \(g=9,81\frac{m}{s^2}\).
-
Anfangsauslenkung oder auch Startauslenkung \(x_0\) ist die Auslenkung welche zu Beginn festgelegt wird.
-
Die Amplitude ist die maximale Auslenkung aus der Ruhelage, die das Fadenpendel im laufe der Schwingung erreicht.
-
Die Gewichtskraft \(F_g=m\cdot g\) wirkt senkrecht nach unten und führt beim ausgelenkten Pendel zu einer Rücktreibenkraft \(F_{rück}\).
-
Die Rückstellkraft \(F_{rück}\) ist die Tangentialkomponente der Gewichtskraft und wird daher auch als \(F_{G,tan}\) bezeichnet.
-
Der Auslenkungswinkel \(\varphi\) ist der Winkel zwischen dem Faden im ausgelenkten Zustand und in der Ruhelage.
Fadenpendel Schwingungsgleichung
Die Schwingung des Fadenpendels um die Ruhelage wird verursacht aufgrund einer rücktreiben Kraft \(F_{rück}\). Die rücktreibende Kraft wirkt in Richtung der Ruhelage und führt so zu einer Beschleunigung des Pendelkörpers dorthin. Durch die Trägheit des Pendelkörpers, bewegt sich dieser jedoch über die Ruhelage hinaus. Wodurch wieder eine rücktreibende Kraft entsteht, welches das Pendel zurück zur Ruhelage zwingt. Es kommt somit zu einer "hin und her" Bewegung (Schwingung) um die Ruhelage. Um die Schwingungsgleichung vom Fadenpendel herleiten zu können muss man somit die Rückstellkraft ermitteln.
Wie in der unteren Skizze gezeigt, kann die Gewichtskraft \(F_{G}=m\cdot g\) in eine Normalkomponente \(F_{G,nor}\) und eine Tangentialkomponente \(F_{G,tan}\) zerlegt werden. Die Normalkomponente \(F_{G,nor}\) wirkt entlang des Fadens. Die Tangentialkomponente \(F_{G,tan}\) wirkt tangential zur Flugbahn des Pendelkörpers, sie bildet die Rückstellkraft, welche die Schwingung des Pendels verursacht.
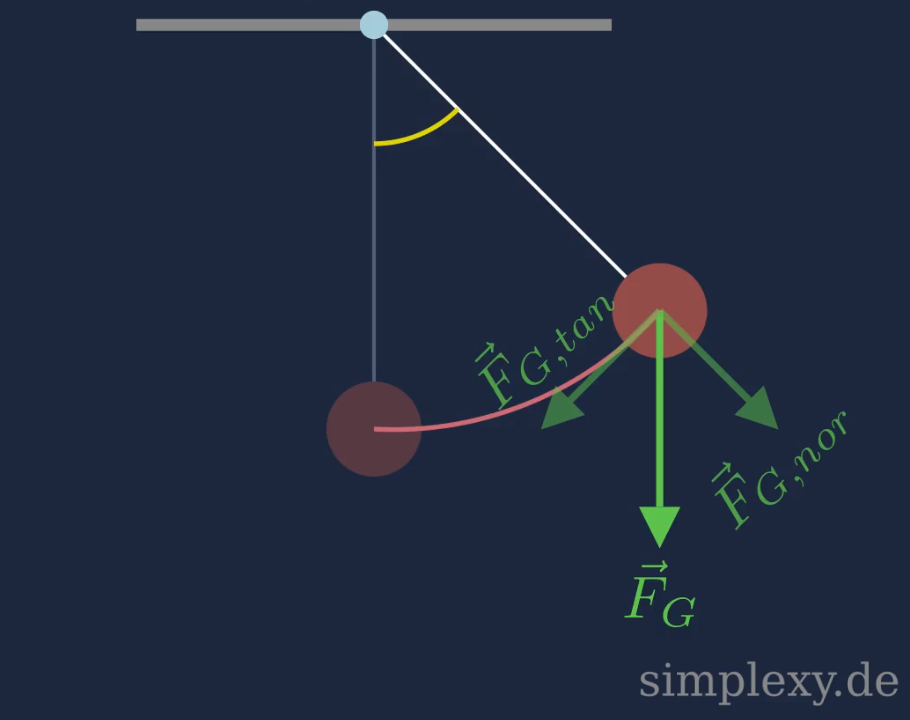
Schwingungsgleichung
Die Schwingungsgleichung oder auch Bewegungsgleichung vom Fadenpendel beschreibt die zeitliche Entwicklung der Auslenkung. Eine Schwingungsgleichung ist in der Regel eine Differentialgleichung zweiter Ordnung. Für die Herleitung einer Schwingungsgleichung wird meistens vom 2. Newtonschen Axiom ausgegangen.
\(F=m\cdot a \)
Um die Schwingungsgleichung vom Fadenpendel aufzustellen müssen die oben genannten Annahmen beachtet werden und ein geeignetes Koordinatensystem eingeführt werden.
Koordinatensystem für das Fadenpendel
Der Pendelkörper bewegt sich entlang eines Kreisbogens \(S\).
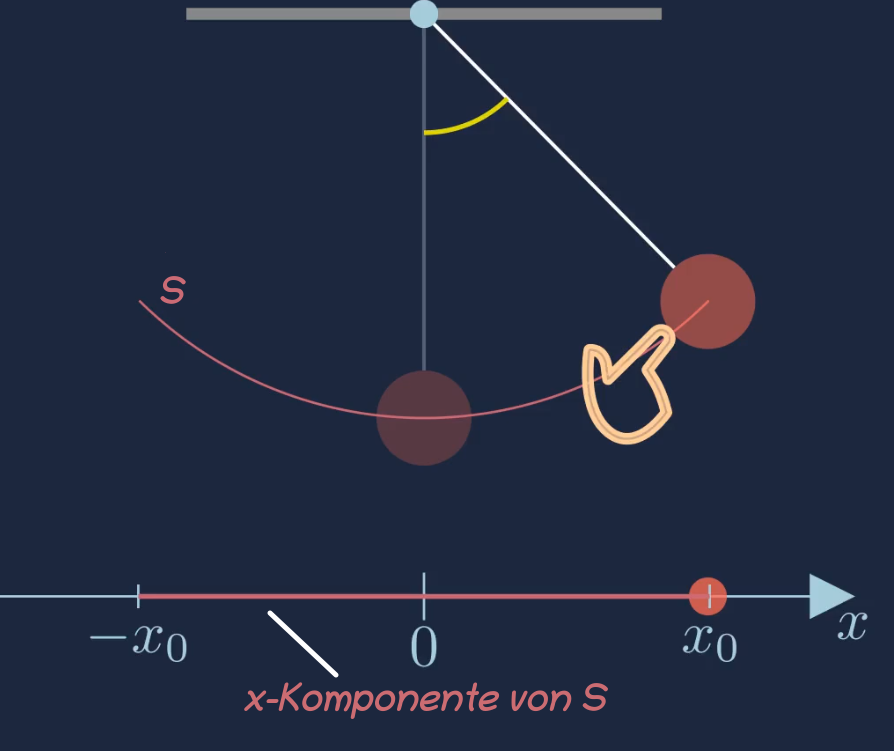
Der Kreisbogen kann in eine \(x\)-Komponente und einer \(y\)-Komponente zerlegt werden. In der unteren Abbildung ist der Größenvergleich zwischen dem Kreisbogen und dessen \(x\)-Komponente dargestellt.
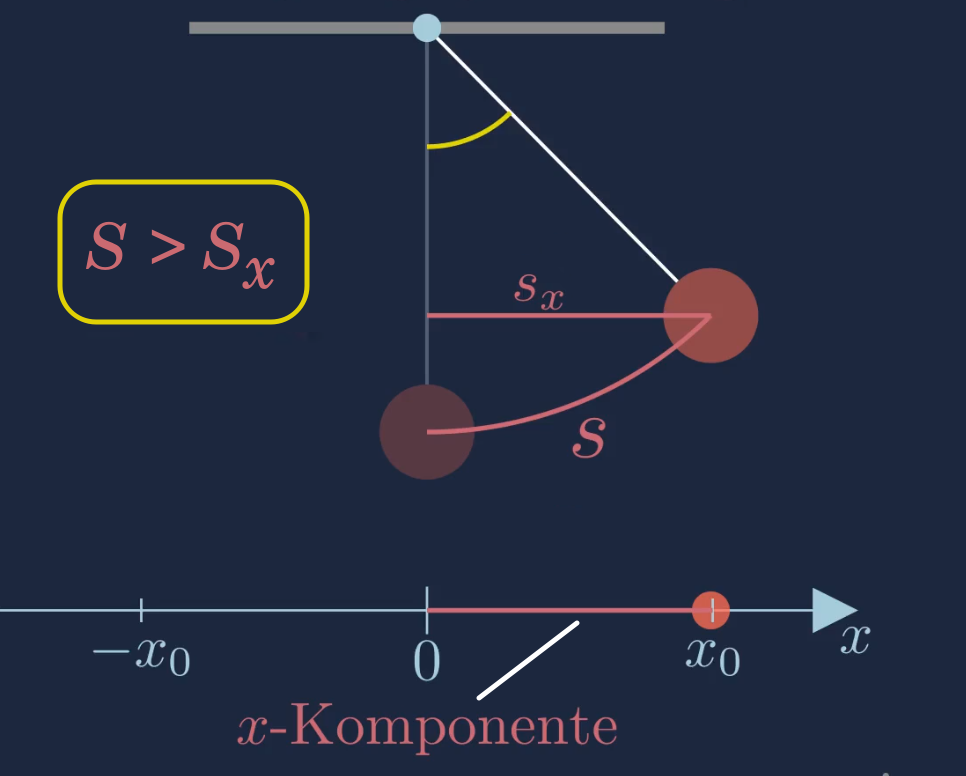
Der Kreisbogen ist deutlich länger als die \(x\)-Komponente \(S_x\). Betrachtet man jedoch nur eine kleine Auslenkung, so ist der Kreisbogen \(S\) und dessen \(x\)-Komponente \(S_x\) annähernd gleich groß.
\(S\approx S_x\)
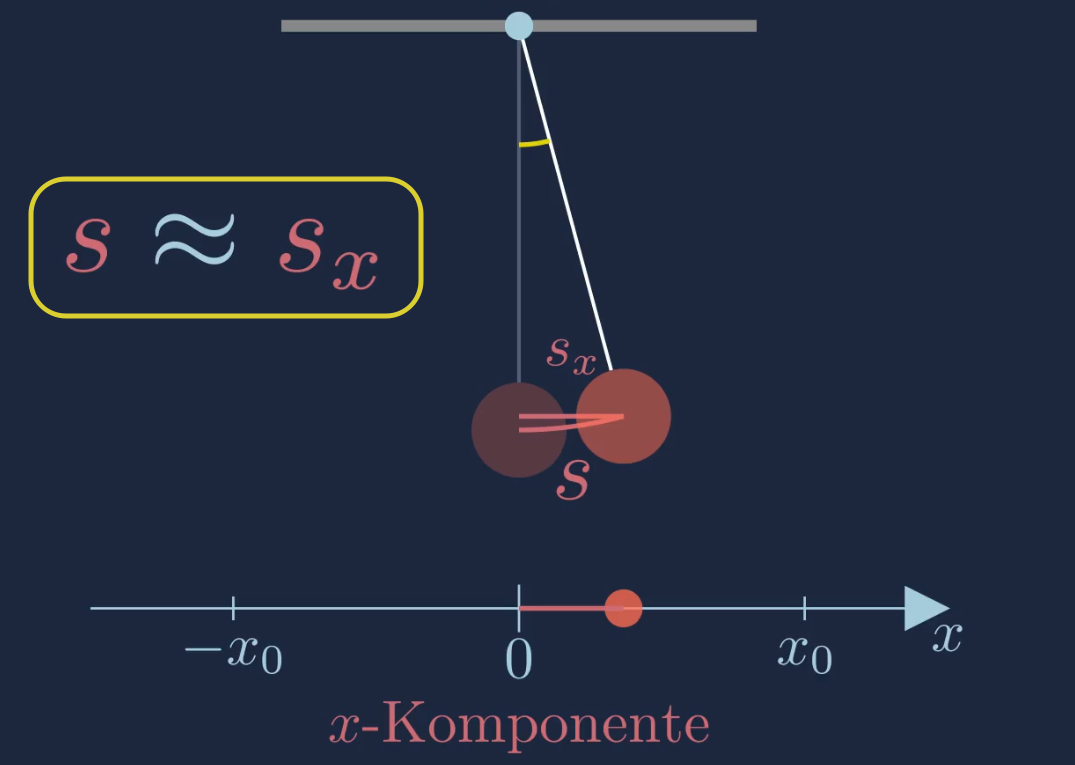
Wir gehen bei der Herleitung der Bewegungsgleichung (Schwingungsgleichung) stets von einer kleinen Auslenkung aus. Damit können wir annehmen, dass sich der Pendelkörper lediglich entlang der \(x\)-Komponente bewegt. Diese \(x\)-Komponente wird von nun an als Auslenkung \(x(t)\) des Fadenpendels definiert.
Info
Eine entsprechend zum Kreisbogen gebogenes Koordinatensystem, dessen Nullpunkt in der Ruhelage liegt kann ebenfalls zur Herleitung der Schwingungsgleichung herangezogen werden. Dabei muss jedoch die sogenannte Kleinwinkelnäherung verwendet werden. Diese ist ähnlich wie in der hier betrachtet Herleitung nur für kleine Auslenkungen anwendbar.
Die Rückstellkraft
Die Bewegung des Pendelkörpers wird als Reibungsfrei angenommen. Auf den Pendelkörper wirken somit lediglich zwei Kräfte. Zum einen die Gewichtskraft \(F_G\) und zum anderen die Kraft des Fadens. Die Normalkomponente der Gewichtskraft \(F_{G,nor}\) wird durch die Kraft des Fadens kompensiert. Die Tangentialkomponente der Gewichtskraft \(F_{G,tan}\) führt zur Beschleunigung des Pendelkörpers in Bahnrichtung. Die für die Schwingung des Pendels relevante Rückstellkraft ist damit die Tangentialkomponente der Gewichtskraft.
\(F_{rück}=F_{G,tan}\)
Herleitung der Schwingungsgleichung
Zur Herleitung der Schwingungsgleichung vom Fadenpendel nutzen wir das 2. Newtonsche Axiom in Bezug auf die Tangentialkomponente der Gewichtskraft.
\( F_{G,tan}=m\cdot a \)
Dabei ist \(m\) die Masse des Pendelkörpers und \(a\) seine Beschleunigung. Während der Schwingung des Pendels ändert der Pendelkörper seine Geschwindigkeit. So ist die Geschwindigkeit an den Umkehrpunkten Null und beim Durchgang durch die Ruhlage, ist die Geschwindigkeit am höchsten. Die Geschwindigkeit ist also eine Funktion der Zeit, dies gilt auch für die Beschleunigung \(a\). Die Abhängigkeit der Beschleunigung von der Zeit wird über die Schreibweise \(a(t)\) ausgedrückt.
\( F_{G,tan}=m\cdot a(t) \)
Nun muss \(F_{G,tan}\) schrittweise analysiert werden. Dazu betrachten wir die folgende Skizze.
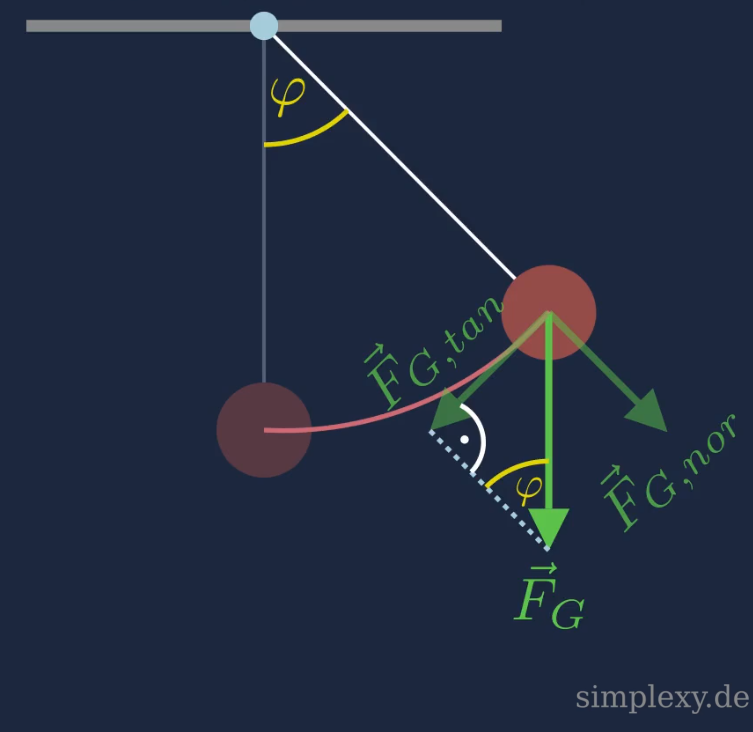
Der Auslenkungswinkel \(\varphi\) findet sich auch im Kräfteparallelogramm wieder. Aus dem Sinussatz ergibt sich der folgende Zusammenhang:
\(\begin{aligned} sin(\varphi)&=\frac{F_{G,tan}}{F_{G}}\\ &\implies\\ F_{G,tan}&=F_G\cdot sin(\varphi) \end{aligned}\)
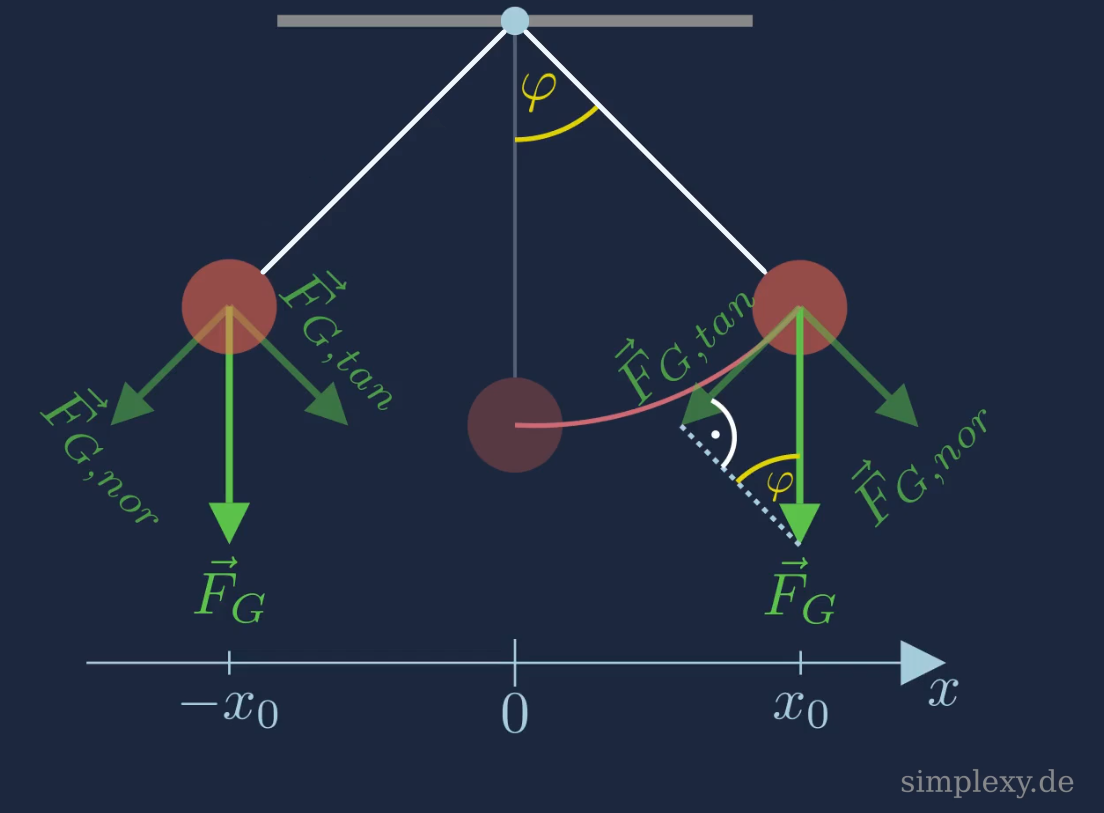
Wie man aus der obigen Skizze entnehmen kann, zeigt die Tangentialkomponente der Gewichtskraft stets gegen die Position \(x\) des Pendelkörpers. Befindet sich der Pendelkörper auf der positiven Hälfte der \(x\)-Achse, so zeigt \(F_{G,tan}\) nach Links in Richtung negativer Werte. Befindet sich der Pendelkörper hingegen auf der negativen Hälfte des Koordinatensystems, so zeigt \(F_{G,tan}\) nach rechts in Richtung positiver \(x\)-Werte. Die Tangentialkomponente ist damit stets entgegen der Orientierung des Koordinatensystems gerichtet. Daher gilt:
\(F_{G,tan}=-F_G\cdot sin(\varphi)\)
Die Formel für die Gewichtskraft
\(F_G=m\cdot g\)
kann nun ersetzt werden:
\(\begin{aligned} F_{G,tan}=-m\cdot g\cdot sin(\varphi) \end{aligned}\)
Für kleine Winkel \(\varphi\) betrachten wir die Bewegung des Pendelkörpers als eindimensional entlang der \(x\)-Achse. Es wird also lediglich die \(x\)-Komponente des Kreisbogens berücksichtigt.
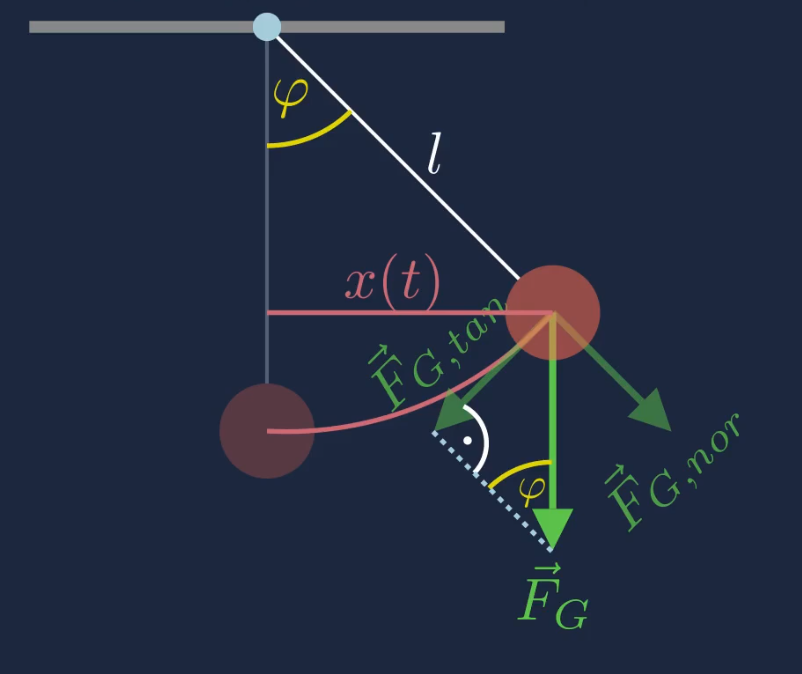
Damit folgt für den \(sin(\varphi)\)
\(\begin{aligned} sin(\varphi)=\frac{x(t)}{l} \end{aligned}\)
Wobei \(x(t)\) die \(x\)-Komponente des Kreisbogens ist und \(l\) die Länge des Fadens.
In den Skizzen ist die Auslenkung groß dargestellt um die Zusammenhänge deutlicher zu sehen.
Für \(F_{G,tan}\) folgt somit:
\(\begin{aligned} F_{G,tan}&=-m\cdot g\cdot \frac{x(t)}{l}\\ &=-m\cdot \frac{g}{l}\cdot x(t)\\ \end{aligned}\)
Nun wird das 2. Newtonsche Axiom angewandt:
\(\begin{aligned} F_{G,tan}&=-m\cdot \frac{g}{l}\cdot x(t)\\ m\cdot a(t)&= -m\cdot \frac{g}{l}\cdot x(t)\\ m\cdot \ddot{x}(t)&= -m\cdot \frac{g}{l}\cdot x(t)\\ \end{aligned}\)
Wobei \(a(t)\) als zweite zeitliche Ableitung der Auslenkung \(x(t)\) geschrieben wurde.
Letztendlich wird die Masse \(m\) gekürzt und man erhält die Schwingungsgleichung bzw. Bewegungsgleichung des Fadenpendels:
\(\begin{aligned} \ddot{x}(t)= - \frac{g}{l}\cdot x(t) \end{aligned}\)
Fadenpendel Schwingungsgleichung
\(\begin{aligned} \ddot{x}(t)+\frac{g}{l}\cdot x(t)=0 \end{aligned}\)
Wobei \(x(t)\) die Auslenkung in Abhängigkeit von der Zeit, \(g\) die Fallbeschleunigung und \(l\) die Länge des Fadens ist.
Info
Die Schwingungsgleichung ist unabhängig von der Masse \(m\) des Pendelkörpers.
Lösung der Schwingungsgleichung
Für die Lösung der Schwingungsgleichung gehen wir von zwei Anfangsbedingungen aus.
-
Der Pendelkörper wird zur Anfangsauslenkung \(x_0\) ausgelenkt.
-
Zum Zeitpunkt \(t=0\) (vor dem Loslassen des Pendels) ist der Pendelkörper in Ruhe und besitzt die Geschwindigkeit \(v(0)=\dot{x}(0)=0\).
Gesucht ist eine Funktion \(x(t)\) welche die Schwingungsgleichung des Fadenpendels, unter Berücksichtigung der Anfangsbedingungen löst. Betrachtet man die Schwingungsgleichung, so fällt auf, das eine Funktion \(x(t)\) gesucht ist, deren zweite Ableitung entgegengesetzt proportional zur Funktion \(x(t)\) ist. Diese Eigenschaft trifft sowohl auf die Sinus-Funktion als auch auf die Cosinus-Funktion zu. Da wir jedoch eine Anfangsbedingung haben, bei der das Pendel zum Zeitpunkt \(t=0\) maximal Ausgelenkt ist (\(x_0\)), kommt der Sinuns wegen \(sin(0)=0\) nicht in Frage. Als Ansatz wird daher die Cosinus-Funktion gewählt.
\(x(t)=x_0\cdot cos(\omega\cdot t)\)
Wobei die Größe \(\omega\) nun bestimmt werden muss. Dazu setzen wir den Ansatz in die Schwingungsgleichung ein:
\(\begin{aligned} \ddot{x}(t)+\frac{g}{l}\cdot x(t)&=0\\ -x_0\cdot \omega^2\cdot cos(\omega \cdot t)+\frac{g}{l}\cdot x_0\cdot cos(\omega\cdot t)&=0\\ -x_0\cdot cos(\omega \cdot t)\bigg(\omega^2 -\frac{g}{l}\bigg) &=0\\ \end{aligned}\)
Die linke Seite der Gleichung kann nur Null sein, wenn der Term in Klammern gleich Null ist.
\(\begin{aligned} -x_0\cdot cos(\omega \cdot t)\bigg(\underbrace{\omega^2 -\frac{g}{l}}_{=0}\bigg)&=0\\ \end{aligned}\)
\(\begin{aligned} \omega^2 -\frac{g}{l}&=0\\ \\ &\implies\\ \\ \omega&=\sqrt{\frac{g}{l}} \end{aligned}\)
Dabei ist \(\omega\) die sogenannte Kreisfrequenz bzw. Eigenfrequenz des Fadenpendels, die wir noch ausführlicher behandeln werden.
Lösung der Schwingungsgleichung
\(\begin{aligned} x(t)=x_0\cdot cos(\omega\cdot t) \end{aligned}\)
Wobei \(\omega\) die Eigenfrequenz bzw. Kreisfrequenz des Pendels ist.
\(\begin{aligned} \omega=\sqrt{\frac{g}{l}} \end{aligned}\)
Zur Probe kann die Lösung \(x(t)\) in die Schwingungsgleichung eingesetzt werden:
\(\begin{aligned} \ddot{x}(t)+\frac{g}{l}\cdot x(t)&=0\\ -x_0\cdot \sqrt{\frac{g}{l}}^2\cdot cos(\sqrt{\frac{g}{l}} \cdot t)+\frac{g}{l}\cdot x_0\cdot cos(\sqrt{\frac{g}{l}}\cdot t)&=0\\ -x_0\cdot\frac{g}{l}\cdot cos(\sqrt{\frac{g}{l}} \cdot t)+\frac{g}{l}\cdot x_0\cdot cos(\sqrt{\frac{g}{l}}\cdot t)&=0\\ -x_0\cdot cos(\sqrt{\frac{g}{l}}\cdot t)\bigg(\underbrace{\frac{g}{l}-\frac{g}{l}}_{=0}\bigg) &=0\\ 0&=0\\ \end{aligned}\)
Die ermittelte Funktion \(x(t)\) löst die Schwingungsgleichung erfolgreich. Nun müssen noch die zwei Anfangsbedingungen überprüft werden:
\(x(0)=x_0\cdot \underbrace{cos(\omega \cdot 0)}_{=1}=x_0\)
Damit ist die erste Anfangsbedingung erfüllt. Darüber hinaus ist auch die zweite Anfangsbedingung erfüllt:
\(v(0)=\dot{x}(t=0)=-x_0\cdot\omega\cdot\underbrace{sin(\omega\cdot 0)}_{=0}=0\)
Zur Überprüfung der zweiten Anfangsbedingung wurde die Geschwindigkeit \(v(t)\) über die erste zeitliche Ableitung der Auslenkung \(x(t)\) ermittelt.
\(v(t)=\dot{x}(t)=-x_0\cdot \omega\cdot sin(\omega t)\)
Periodendauer Fadenpendel
Die Periodendauer bzw. die Schwingungsdauer vom Fadenpendel ist die Zeit, die das Pendel für eine vollständige "hin und her" Bewegung benötigt. Sprich einmal vom einen Umkehrpunkt zum anderen Umkehrpunkt und wieder zurück zum ursprünglichen Umkehrpunkt. Die Periodendauer hat das Formelzeichen \(T\) und die Einheit Sekunden \([s]\).
In dem obigen Video ist der Zusammenhang zwischen der Periodendauer und der Kreisfrequenz erläutert. Es gilt:
\(\begin{aligned} \omega=\frac{2\pi}{T} \end{aligned}\)
Gleichzeitig wissen wir, das die Kreisfrequenz über folgende Formel bestimmt ist:
\(\begin{aligned} \omega=\sqrt{\frac{g}{l}} \end{aligned}\)
Beide Formel können somit gleichgesetzt werden, wodurch der folgende Zusammenhang entsteht:
\(\begin{aligned} \sqrt{\frac{g}{l}}&=\frac{2\pi}{T}\\ &\implies\\ T&=2\cdot \pi\cdot\sqrt{\frac{l}{g}} \end{aligned}\)
Periodendauer bzw. Schwingungsdauer
\(\begin{aligned} T&=2\cdot \pi\cdot\sqrt{\frac{l}{g}} \end{aligned}\)
Die Periodendauer gibt an wie lange das Fadenpendel für eine vollständige Schwingung (Periode) benötigt. Die Periodendauer hat die Einheit Sekunde \([s]\).
Wie man aus der Formel sehen kann, ist die Periodendauer von der Länge \(l\) des Fadens und der Fallbeschleunigung \(g\) abhängig. Befindet man sich auf der Erde, so entspricht die Fallbeschleunigung der Erdbeschleunigung \(g=9,81\frac{m}{s^2}\). Die Erdbeschleunigung ist eine Konstante und somit hängt die Periodendauer bzw. die Schwingungsdauer lediglich von der Fadenlänge ab.
Je länger der Faden des Pendels ist, desto größer ist die Periodendauer \(T\). Wie weit das Pendel aus der Ruhelage ausgelenkt wird (Startauslenkung \(x_0\)) ist, spielt keine Rolle.
Frequenz Fadenpendel
Die Frequenz vom Fadenpendel gibt an, wie viele Perioden (vollständige hin und her Bewegungen) innerhalb einer Sekunde stattfinden. Die Frequenz berechnet sich über den Kehrwert der Periodendauer.
Fadenpendel Frequenz
\(\begin{aligned} f=\frac{1}{T} \end{aligned}\)
Die Frequenz gibt an, wie viele Perioden innerhalb einer Sekunde stattfinden. Die Frequenz hat die Einheit \(\big[\frac{1}{s}\big]\).
Die Frequenz vom Fadenpendel kann auch über die Länge \(l\) des Fadens ausgedrückt werden. Dazu muss die Formel der Frequenz nach \(T\) umgestellt werden und mit der Formel für die Periodendauer gleichgesetzt werden.
Wir setzen
\(\begin{aligned} T=\frac{1}{f} \end{aligned}\)
und
\(\begin{aligned} T=2\pi\cdot \sqrt{\frac{l}{g}} \end{aligned}\)
gleich, und erhalten:
\(\begin{aligned} \frac{1}{f}=2\pi\cdot \sqrt{\frac{l}{g}} \end{aligned}\)
\(\implies\)
\(\begin{aligned} f=\frac{1}{2\pi}\cdot\sqrt{\frac{g}{l}} \end{aligned}\)
Frequenz und Fadenlänge
\(\begin{aligned} f=\frac{1}{2\pi}\cdot\sqrt{\frac{g}{l}} \end{aligned}\)
Je länger der Faden ist, desto kleiner ist die Frequenz.
Fadenpendel Geschwindigkeit
Wir wissen nun wie die Ort-Zeit-Funktion von Fadenpendel lautet. Das Fadenpendel vollführt eine harmonische Schwingung mit der Ort-Zeit-Funktion
\(\begin{aligned} x(t)=x_0\cdot cos(\omega\cdot t) \end{aligned}\)
Wobei \(\omega\) die Kreisfrequenz des Pendels ist.
Wie kann man die Geschwindigkeit vom Fadenpendel berechnen?
Um dieser Frage nachzugehen befassen wir uns zunächst mit der Bewegung des Fadenpendels, sobald man es loslässt.
Wir nehmen an, dass zum Zeitpunkt \(t=0\) das Fadenpendel zum Umkehrpunkt \(x_0\) ausgelenkt ist. Sobald das Fadenpendel los gelassen wird, wird es sich in Richtung der Ruhelage beschleunigen. Dabei nimmt die Beschleunigung des Pendels zu. Die maximal Geschwindigkeit erreicht das Pendel beim Durchgang durch die Ruhelage. Durch die Trägheit des Pendelkörpers bewegt sich das Pendel über die Ruhelage hinaus zum anderen Umkehrpunkt bei \(-x_0\). Dabei nimmt die Geschwindigkeit ab und erreicht schlussendlich am Umkehrpunkt \(-x_0\) die Geschwindigkeit \(v=0\). Im Anschluss findet wieder eine Beschleunigung statt, die dass Fadenpendel erneut in Richtung der Ruhelage beschleunigt.
Aus der Mechanik wissen wir, das die Geschwindigkeit ganz allgemein über die zeitliche Ableitung der Ort-Zeit-Funktion \(\dot{x}(t)\) berechnet werden kann. Das gleiche gilt auch für den zeitlichen Verlauf der Geschwindigkeit vom Fadenpendel.
Geschwindigkeit
\(v=\)\(\frac{\Delta s}{\Delta t}\)
bzw.
\(v(t)=\dot{x}(t)\)
Um den zeitlichen Verlauf der Geschwindigkeit zu ermitteln müssen wir also die Ort-Zeit-Funktion des Pendels einmal nach der Zeit ableiten.
\(\begin{aligned} x(t)&=x_0\,\,cos(\omega t)\\ \\ \dot{x}(t)&=-x_0\cdot \omega\cdot sin(\omega t) \end{aligned}\)
Hinweis
Bei der Ableitung von \(x(t)\) wurde verwendet:
\(cos(\omega t)'=-\omega\cdot sin(\omega t)\)
Die Ableitung vom Cosinus ist der Minus Sinus. Des Weiteren wurde die Kettenregel verwendet.
Geschwindigkeit Fadenpendel
\(v(t)=-x_0\cdot \omega\cdot sin(\omega t)\)
Wie sieht der zeitliche Verlauf der Geschwindigkeit für das Fadenpendel aus?
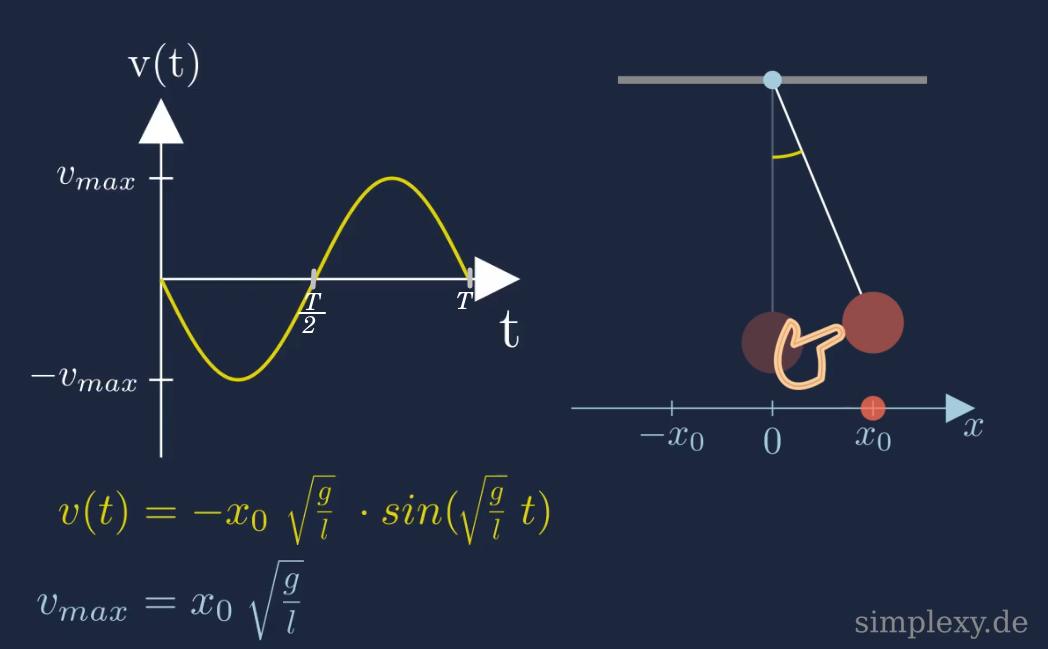
In der oberen Graph sieht man, den Verlauf der Geschwindigkeit in Abhängigkeit von der Zeit. Sobald das Fadenpendel los gelassen wird, bewegt es sich in Richtung der Ruhelage und die Geschwindigkeit nimmt zu. Da die Bewegung zu Beginn nach Links verlauft (zu kleineren \(x\)-Werten) ist die Geschwindigkeit negativ. Sobald das Fadenpendel die Ruhelage erreicht hat, ist die Geschwindigkeit maximal (\(-v_{max}\)). Das Fadenpendel bewegt sich anschließend zum andere Umkehrpunkt bei \(-x_0\) und verliert dabei an Geschwindigkeit. Am anderen Umkehrpunkt angekommt, ist die Geschwindigkeit auf Null gefallen. Im Anschluss wird die Masse wieder in Richtung der Ruhelage beschleunigt und die Geschwindigkeit nimmt wieder zu. Beim zweiten Durchgang durch die Ruhelage ist die Geschwindigkeit wieder maximal (\(v_{max}\)). Während das Pendel zum Umkehrpunkt \(x_0\) schwingt, nimmt die Geschwindigkeit erneut ab und wird schlussendlich wieder Null.
Merke
Die hier betrachtete Ort-Zeit-Funktion \(x(t)=x_0\cdot cos(\omega\cdot t)\), geht einher mit einem Fadenpendel das zum start Zeitpunkt \(t=0\) nach Rechts ausgelenkt ist (\(x_0\)). Man kann das Fadenpendel zum start Zeitpunkt in der Ruhelage lassen und dann nach rechts anstoßen. Die Ort-Zeit-Funktion wäre dann:
\(x(t)=x_0\cdot sin(\omega\cdot t)\)
und damit wäre die Geschwindigkeit für diesen Fall:
\(v(t)=x_0\cdot \omega\cdot cos(\omega t)\)
Die Ort-Zeit-Funktion und damit auch der zeitliche Verlauf der Geschwindigkeit ist von der Anfangsbedingung abhängig.
Fadenpendel Beschleunigung
Über das gleiche Vorgehen kann auch die Beschleunigung vom Fadenpendel berechnet werden.
Um den zeitlichen Verlauf der Beschleunigung vom Fadenpendel zu erhalten, muss die Ort-Zeit-Funktion zwei mal nach der Zeit abgeleitet werden \(\ddot{x}(t)\).
Beschleunigung
\(a=\)\(\frac{\Delta v}{\Delta t}\)
bzw.
\(a(t)=\dot{v}(t)=\ddot{x}(t)\)
Wir müssen also nun die Ort-Zeit-Funktion \(x(t)\) zwei mal nach der Zeit ableiten oder die Geschwindigkeit \(v(t)\) einmal nach der Zeit ableiten um auf die Beschleunigung vom Pendel zu kommen.
Beschleunigung vom Fadenpendel
\(a(t)=\dot{v}(t)\)
\(a(t)=-x_0\cdot \omega^2\cdot cos(\omega\cdot t)\)
Wir haben auch hier die Kettenregel verwendet um die Ableitung zu berechnen.
Die äußeren Ableitung von \(-sin(\omega t)\) lautet:
\(-cos(\omega\cdot t)\)
und die innere Ableitung lautet:
\(\begin{aligned} (\omega\cdot t)'=\omega \end{aligned}\)
Die innere Ableitung mal die äußere Ableitung liefert also:
\(a(t)=-x_0\cdot \omega^2\cdot cos(\omega t)\)
Der zeitliche Verlauf der Beschleunigung sieht wie folgt aus:
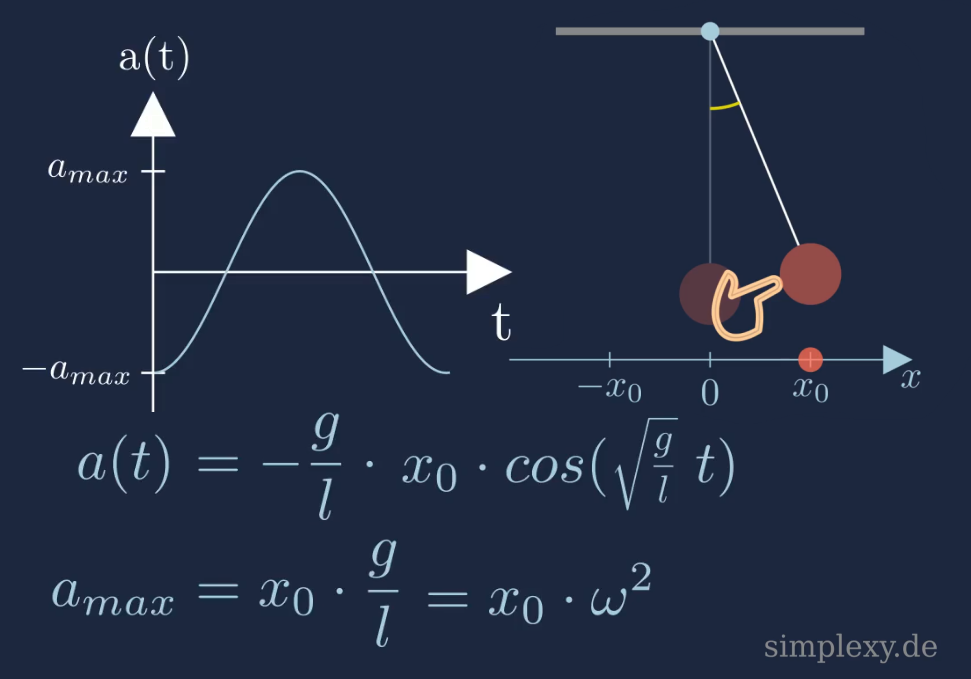
Wie man in der oberen Abbildung sieht, ist die Beschleunigung an den Umkehrpunkten maximal. Dies liegt daran, das an den Umkehrpunkten ein Richtungswechsel stattfindet. Beim Durchgang durch die Ruhelage ist die Beschleunigung Null.
Fadenpendel Energiebetrachtung
Beim ungedämpften Fadenpendel existieren zwei Energieformen welche sich fortlaufend ineinander umwandeln. Die zwei Energieformen sind die kinetische und die potentielle Energie. Die Gesamtenergie vom Fadenpendel besteht aus der Summe der potentiellen und der kinetischen Energie. Das ungedämpfte Fadenpendel ist ein abgeschlossenes System, wodurch die Gesamtenergie immer gleich bleibt.
\(E_{ges}=E_{kin}+E_{pot}=konstant\)
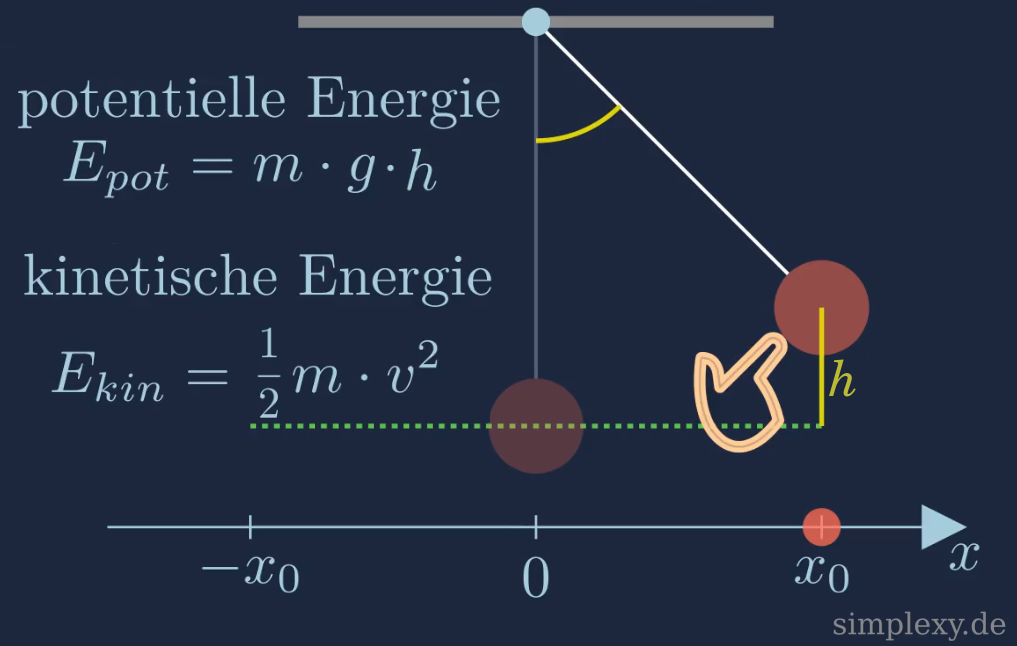
Die kinetische Energie \(E_{kin}\) ist die Bewegungsenergie des Pendelkörpers und berechnet sich über:
\(\begin{aligned} E_{kin}=\frac{1}{2}\cdot m\cdot v^2 \end{aligned}\)
wobei \(v\) die Geschwindigkeit des Pendelkörpers ist.
Die potentielle Energie wird auch als Lage- bzw. Höhenenergie bezeichnet. Sie hängt von der Höhe des Pendelkörpers ab und berechnet sich über:
\(\begin{aligned} E_{pot}=m\cdot g\cdot h \end{aligned}\)
wobei \(h\) die Höhe des Pendelkörpers ist.
Energieerhaltungssatz
Die Gesamtenergie bleibt während der Schwingung des Fadenpendels erhalten. Es findet lediglich eine Umwandlung zwischen kinetischer und potentieller Energie statt.
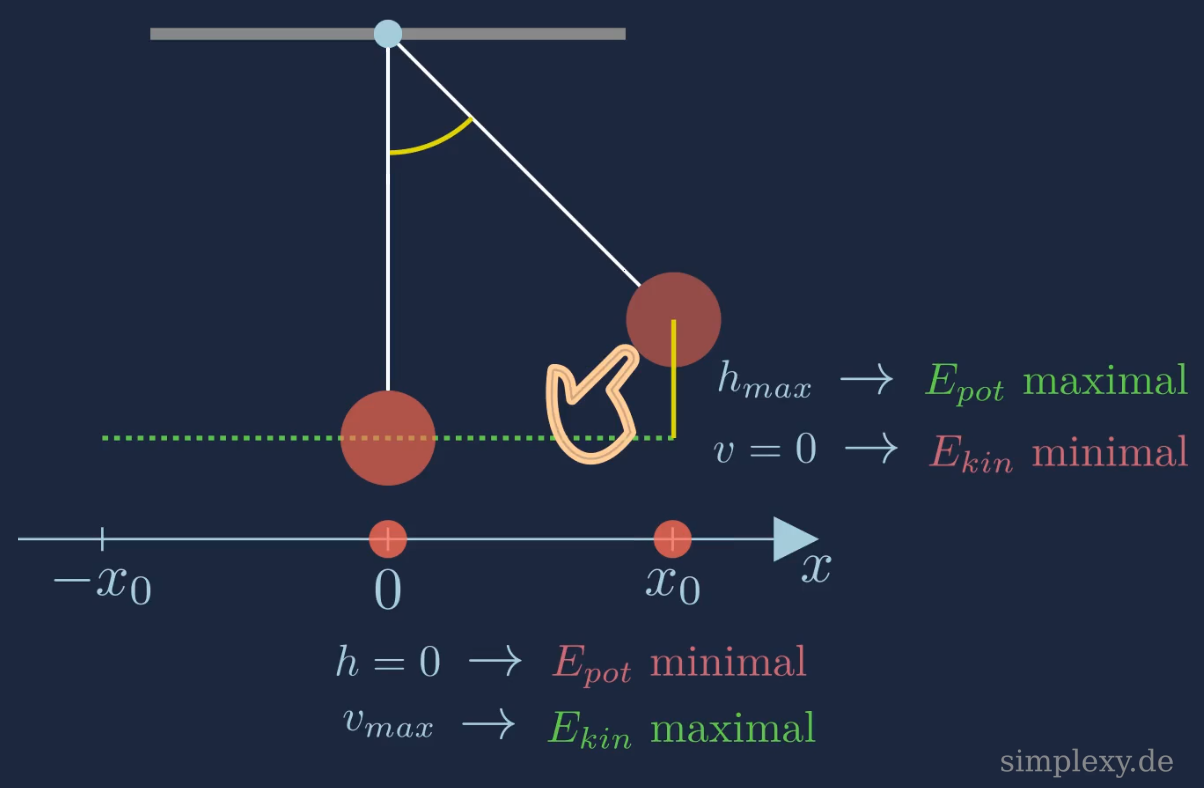
Am Umkehrpunkt (Punkt der maximalen Auslenkung) ist die maximale Höhe erreicht. Damit ist auch die potentielle Energie am höchsten. Die Geschwindigkeit des Pendelkörpers ist am Umkehrpunkt jedoch Null, wodurch die kinetische Energie dort ebenfalls Null ist. Die potentielle Energie entspricht am Umkehrpunkt somit der Gesamtenergie. Sobald sich der Pendelkörpers in Richtung der Ruhelage beschleunigt, nimmt seine Geschwindigkeit zu. Es findet somit eine Zunahme der kinetischen Energie statt. Gleichzeitig nimmt die Höhe des Pendelkörpers ab, wodurch die potentielle Energie abnimmt. Beim Durchgang durch die Ruhelage, ist die Geschwindigkeit des Pendelkörpers maximale und die Höhe ist gleich Null. Die potentielle Energie ist somit Null und die kinetische Energie entspricht der Gesamtenergie.
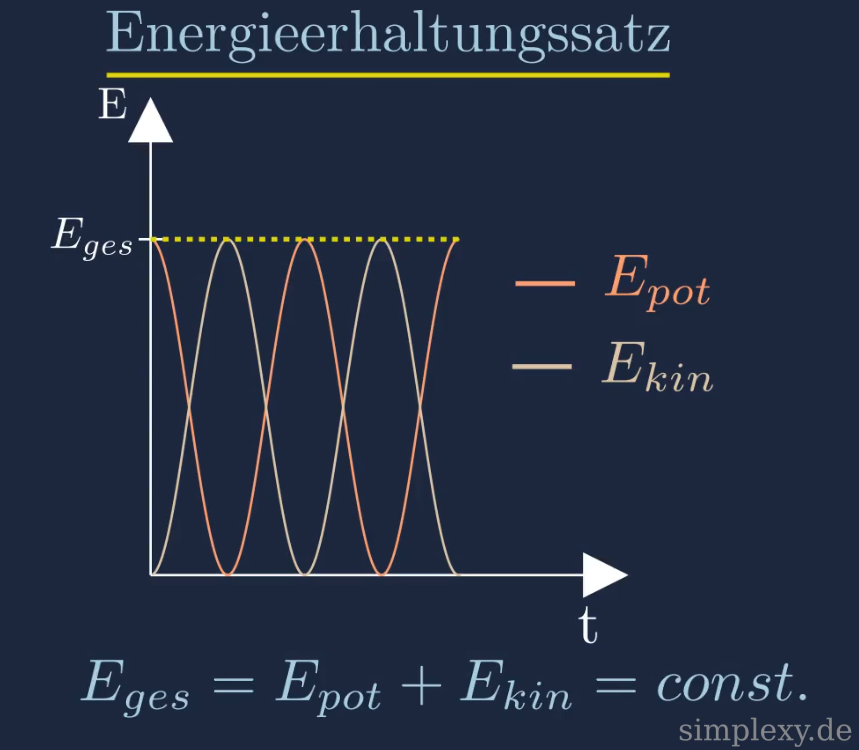
In der oberen Abbildung ist der zeitliche Verlauf der kinetischen und der potentiellen Energie dargestellt.
