Gedämpfte Schwingung
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Was ist eine gedämpfte Schwingung?
Die gedämpfte Schwingung ist eine Sonderform der harmonischen Schwingung. Dabei bewegt sich ein Körper periodisch um eine Ruhelage bzw. Gleichgewichtslage. Bei der gedämpften Schwingung ist eine Dämpfung vohanden, welche die Amplitude der Schwingung zur Abnahme zwingt.
Die Abnahme der Amplitude ist durch Reibungsverluste charakterisierbar. Betrachtet man eine harmonische Schwingung in der Luft, so führt die Luftreibung zu einem Luftwiderstand, der die Schwingung dämpft. Die entstehende Reibung wird mathematisch durch eine Dämpfungskonstante und eine Abklingkonstante in die Bewegungsgleichung der Schwingung eingebracht.
Gedämpfte Schwingung Gleichung
Die Herleitung der Schwingungsgleichung für das gedämpfte Federpendel ist in dem unteren Video leicht erklärt.
Die gedämpfte harmonische Schwingung wird durch eine Schwingungsgleichung (Differentialgleichung) beschrieben. Je nach dem was für ein System man betrachtet, sind kleine Unterschiede in den Differentialgleichungen möglich. Das Vorgehen und der mathematische Rahmen ist bei allen gedämpften harmonischen Schwingungen gleich. Daher betrachten wir hier als Beispiel den Fall vom gedämpften Federpendel.
Herleitung Gedämpfte harmonische Schwingung
Die Dämpfung beim Federpendel macht sich bemerkbar über eine zeitliche Abnahme der Amplitude. Die Dämpfung kommt zustande, weil das Pendel mit dem Medium in dem es Schwingt wechselwirkt. Findet die Schwingung beispielsweise in Luft statt, so herrscht ein Luftwiderstand, der das Pendel abbremst. Das Pendel muss die Luft verdrängen in dem es Schwingt, dies sorgt für Reibungsverluste und das Federpendel wird abgebremst. Mathematisch wird die Dämpfung über eine Dämpfungskonstante \(k\) und eine Abklingkonstante \(\delta\) beschrieben.
Gedämpftes Federpendel
Um die gedämpfte Schwingung eines Federpendels mathematisch beschreiben zu können, muss der Einfluss der Luftreibung berücksichtigt werden. Zusätzlich zu der Beschleunigungskraft und der Federkraft
\(m\cdot \ddot{s}(t)=-D\cdot s(t)\)
muss die Kraft welche durch die Luftreibnung zu stande kommt berücksichtigt werden. Dabei ist die Luftreibung proportional zu der Geschwindigkeit \(v(t)\) des Pendels. Die Formel für die Kraft durch die Luftreibung lautet wie folgt.
Luftreibung
\(F_{LR}=k\cdot v(t)\)
Dabei ist \(k\) die Reibungskonstante mit der Einheit \([N\cdot \frac{s}{m}]\).
Die Reibungskonstante \(k\) ist im allgemeinen eine Zahl die in der Aufgabenstellung vorgegeben wird. Trotzallem steckt in der Reibungskonstante viel Information. Sie ist abhängig von der Wechselwirkung zwischen dem Pendel und der Luft. Sie ist beispielsweise von der Form der Masse am Pendel abhängig. Je aerodynamischer die Pendelmasse ist, desto kleiner ist die Reibungskonstante. In anderen Worten, je besser die Luft verdrängt wird, desto kleiner ist der Einfluss der Luftreibung auf die Bewegung des Pendels. Ein weiterer wichtiger Aspekt ist das Medium selbst. Ein Pendel kann auch in einer Flüssigkeit schwingen. Eine Flüssigkeit lässt sich schwerer verdrängen als Luft, daher wäre die Reibungskonstante größer. Man kann sich bereits vorstellen, wenn die Viskosität der Flüssigkeit sehr gering ist (bsp. Öl oder Hönig) dann ist die Dämpfungskonstante so groß, dass eine Schwingung des Pendels garnicht möglich ist.
Der Einfluss der Luftreibung lässt sich in die Bewegungsgleichung des Federpendels wie folgt einbringen:
\(m\cdot \ddot{s}(t)=-D\cdot s(t)-\underbrace{k\cdot v(t)}_{F_{LR}}\)
Das Minus vor dem Term für die Luftreibung \(F_{LR}\) kommt daher, dass die Luftreibung in die entgegengesetzte Richtung wie die Bewegungsrichtung wirkt. Bewegt sich das Pendel nach unten, so herrscht ein Luftwiderstand nach oben. Bewegt sich das Pendel nach oben, so drückt der Luftwiderstand nach unten.
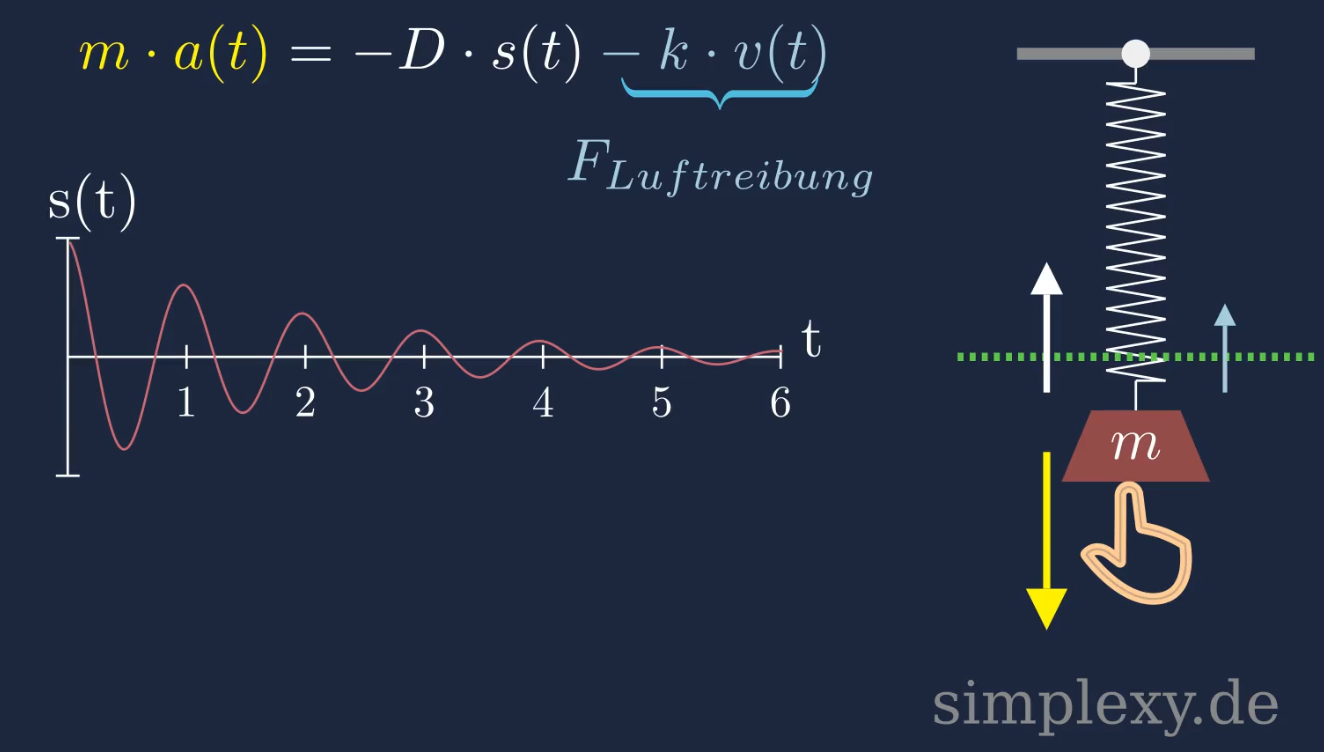
Man kann \(v(t)\) mit \(\dot{s}(t)\) ersetzen so dass man folgende Bewegungsgleichung erhält:
\(m\cdot \ddot{s}(t)=-D\cdot s(t)-k\cdot \dot{s}(t)\)
Diese Bewegungsgleichung kann man nun noch etwas umformen so das man zu der üblichen Form der gedämpften Bewegungsgleichung des Federpendels kommt.
Gedämpfte harmonische Schwingung
\(\ddot{s}(t)+\frac{D}{m}\cdot s(t)+\frac{k}{m}\cdot \dot{s}(t)=0\)
Wie löst man die gedämpfte Bewegungsgleichung?
Um die Bewegungsgleichung des gedämpften Federpendels zu lösen nutzen wir einen "Exponential-Ansatz".
\(\begin{aligned} s(t)&=c\cdot e^{\lambda t}\\ \dot{s}(t)&=c\cdot\lambda\,\,e^{\lambda t}\\ \ddot{s}(t)&=c\cdot\lambda^2\,\,e^{\lambda t} \end{aligned}\)
Setzt man den Ansatz in die gedämpfte Bewegungsgleichung ein, so erhält man:
\( \lambda^2\,c\,e^{\lambda t}+\frac{D}{m}\,c\,e^{\lambda t}+\frac{k}{m}\,\lambda\,c\,e^{\lambda t}=0 \)
Nun können wir den Term \(c\,e^{\lambda t}\) kürzen:
\( \lambda^2\,\bcancel{c\,e^{\lambda t}}+\frac{D}{m}\, \bcancel{c\,e^{\lambda t}}+\frac{k}{m}\,\lambda\,\bcancel{c\, e^{\lambda t}}=0 \)
Übrig bleibt eine quadratische Gleichung, die mit der pq-Formel gelöst werden kann.
\( \lambda^2+\frac{k}{m}\,\lambda+\frac{D}{m}=0 \)
\(\implies\)
\( \lambda_{1,2}=-\frac{k}{2m}\pm\sqrt{\big(\frac{k}{2m}\big)^2-\frac{D}{m}} \)
Für eine bessere Darstellung von \(\lambda_{1,2}\), nehmen wir die folgenden Definitionen vor:
\(\begin{aligned} \omega_0&=\sqrt{\frac{D}{m}}\\ \\ \delta&=\frac{k}{2m} \end{aligned}\)
\(\implies\)
\( \lambda_{1,2}=-\delta\pm\sqrt{\delta^2-\omega_0^2} \)
Dabei ist \(\omega_0\) die Eigenfrequenz des ungedämpften Federpendels und \(\delta\) wird als Abklingkonstante bezeichnet. Damit haben wir nun zwei linear unabhängige Lösungen \(s_1(t)\) und \(s_2(t)\)
\(\begin{aligned} s_1(t)&=c_1\cdot e^{\lambda_1 t}\\ \\ s_2(t)&=c_2\cdot e^{\lambda_2 t}\\ \end{aligned}\)
Je nachdem wie die Diskriminante in \(\lambda_{1,2}\) lautet, ändert sich das weitere Vorgehen. Die Wahl von \(\omega_0\) und \(\delta\) können zum Schwingfall, Kriechfall oder den aperiodischen Grenzfall führen.
Schwingfall
Ist die Dämpfungskonstante \(k\) bzw. die Abklingkonstante \(\delta\) kleiner als die Eigenfrequenz \(\omega_0\)
\(\delta^2\lt\omega_0^2\)
so wird die Diskriminante \(\delta^2-\omega_0^2\) aus \(\lambda_{1,2}\) negativ. Der Wurzelausdruck wird damit komplex.
\( \lambda_{1,2}=-\delta\pm\underbrace{\sqrt{\delta^2-\omega_0^2}}_{imaginär} \)
Für eine besser Übersicht definieren wir
\( \omega^2=\omega_0^2-\delta^2 \)
\(\implies\)
\(\begin{aligned} \lambda_{1,2}&=-\delta\pm\sqrt{-\omega^2}\\ \\ &=-\delta\pm\omega\underbrace{\sqrt{-1}}_{i}\\ \\ &=-\delta\pm i\,\omega \end{aligned}\)
Setzt man nun \(\lambda_{1}\) in \(s_1(t)\) ein und \(\lambda_{2}\) in \(s_2(t)\) ein so erhält man:
\(\begin{aligned} s_1(t)&=c_1\cdot e^{(-\delta+i\omega)t}\\ \\ s_2(t)&=c_2\cdot e^{(-\delta-i\omega)t} \end{aligned}\)
Jede beliebige Lösung \(s(t)\) kann als linear kombination von \(s_1(t)\) und \(s_2(t)\) geschrieben werden.
\(\begin{aligned} s(t)&=c_1 e^{(-\delta+i\omega)t}+c_2 e^{(-\delta-i\omega)t}\\ \\ &=e^{-\delta t}\big(\underbrace{c_1e^{i\omega t}+c_2e^{-i\omega t}}_{A\,cos(\omega\,t+\varphi)}\big)\\ \\ &=A\,e^{-\delta t}\,cos(\omega\,t+\varphi) \end{aligned}\)
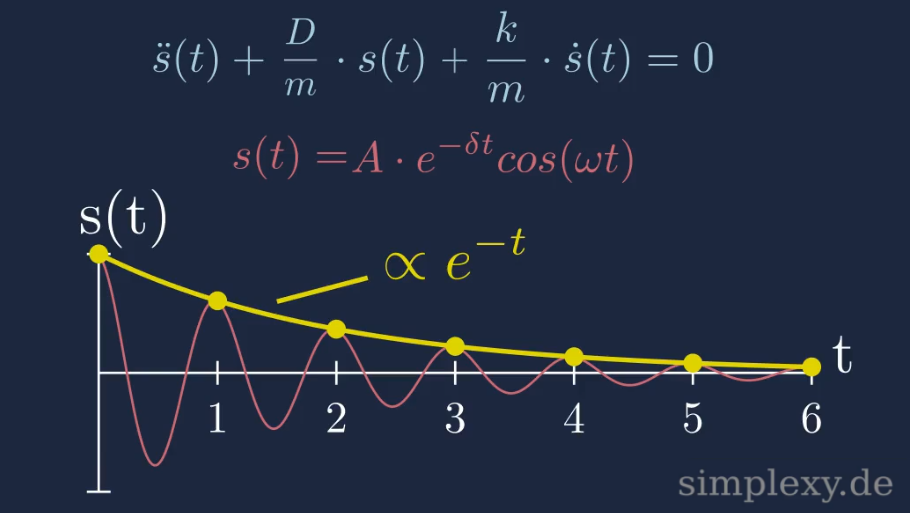
Im Schwingfall vollführt das Pendel eine periodische Bewegung mit einer exponentiell abnehmenden Amplitude.
Kriechfall
Der Kriechfall entsteht wenn die Dämpfungskonstante \(k\) bzw. Abklingkonstante \(\delta\) größer als die Eigenfrequenz des Pendels ist.
\(\delta^2\gt\omega^2\)
Im Kriechfall ist die Diskriminante von \(\lambda_{1,2}\) positiv. Die Lösungen \(s_1(t)\) und \(s_2(t)\) sind damit reell.
\( \lambda_{1,2}=-\delta\pm\underbrace{\sqrt{\delta^2-\omega^2}}_{\alpha} \)
\(\implies\)
\(\begin{aligned} s_1(t)&=c_1\cdot e^{(-\delta+\alpha)t}\\ \\ s_2(t)&=c_2\cdot e^{(-\delta-\alpha)t} \end{aligned}\)
Eine beliebige Lösung \(s(t)\) kann als linear kombination von \(s_1(t)\) und \(s_2(t)\) ausgedrückt werden.
\(\begin{aligned} s(t)&=c_1 e^{(-\delta+\alpha)t}+c_2 e^{(-\delta-\alpha)t}\\ \\ &=e^{-\delta t}\big(c_1e^{\alpha t}+c_2e^{-\alpha t}\big)\\ \end{aligned}\)
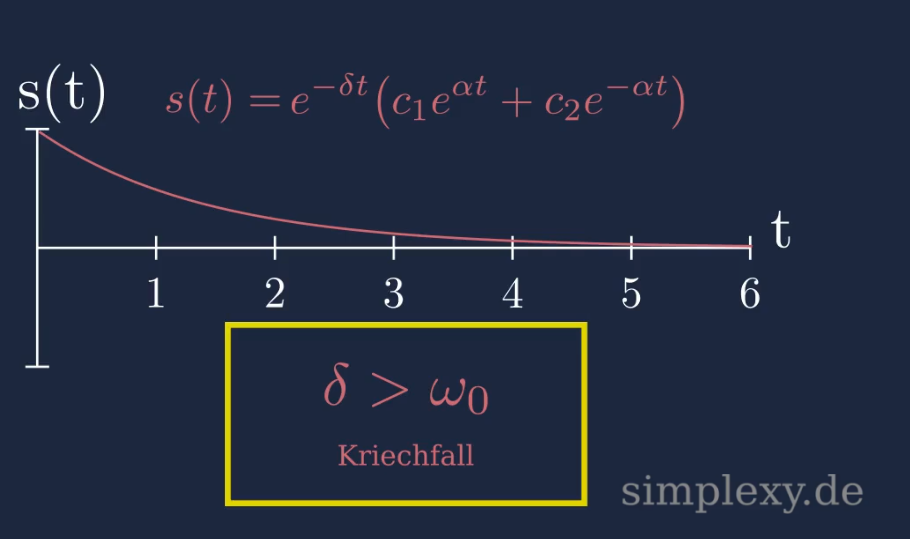
Im Kriechfall ist kein Schwingungsterm in der Lösung \(s(t)\) vorhanden. Das Federpendel bewegt sich in Richtung der Ruhelage und verbleibt dort. Dies liegt an der hohen Dämpfungskonstante \(k\) bzw. der hohen Abklingkonstante \(\delta\). So ein Verhalten ist beispielsweise in einer Flüssigkeit mit geringer Viskosität (Öl, Honig, etc.) zu beobachten.
Aperiodischer Grenzfall
Beim aperiodischen Grenzfall ist die Abklingkonstante \(\delta\) so groß wie die Eigenfrequenz \(\omega_0\)
\(\delta^2=\omega_0^2\)
\( \lambda_{1,2}=-\delta\pm\underbrace{\sqrt{\delta^2-\omega^2}}_{=0} \)
\(\implies\)
\(\begin{aligned} s_1(t)&=c_1\cdot e^{-\delta t}\\ \\ s_2(t)&=c_2\cdot e^{-\delta t} \end{aligned}\)
Damit sind \(s_1(t)\) und \(s_2(t)\) nicht mehr linear unabhängig. Da die gedämpfte Differentialgleichung des Pendels eine dgl zweiter Ordnung ist, müssen zwei linear unabhängige Lösung vorhanden sein. Um \(s_1(t)\) und \(s_2(t)\) linear unabhängig zu machen, kann man bei einem der zwei ein \(t\) hinzu multiplizieren. Wir machen dies bei \(s_2(t)\)
\(\begin{aligned} s_1(t)&=c_1\cdot e^{-\delta t}\\ \\ s_2(t)&=c_2\cdot t\,\cdot e^{-\delta t} \end{aligned}\)
Trotz der multiplikation mit \(t\) bei \(s_2(t)\), ist das eine Lösung der Differentialgleichung für den Fall, dass \(\omega_0=\delta\). Als Probe kann man \(s_2(t)\) in die dgl einsetzten, man stellt fest, dass es sich dabei um eine valide Lösung handelt. Damit kann nun eine beliebige Lösung \(s(t)\) als linear kombination von \(s_1(t)\) und \(s_2(t)\) geschrieben werden.
\(\begin{aligned} s(t)&=c_1 e^{-\delta t}+c_2\cdot t\, e^{-\delta t}\\ \\ &=e^{-\delta t}\big(c_1+c_2\cdot t\big)\\ \end{aligned}\)

Beim aperiodischen Grenzfall ist die kleinstmögliche Dämpfungskonstante vorhanden, die zu einer Lösung ohne Schwingung führt. Ähnlich wie beim Kriechfall bewegt sich das Federpendel zur Ruhelage ohne eine Schwingung zu vollführen.
Fragen und Antworten
Was sind gedämpfte harmonische Schwingungen?
Eine gedämpfte harmonische Schwingung ist eine Schwingung, bei der Reibungsverluste auftreten welche zu einer zeitlichen oder räumlichen abnahme der Amplitude führen.
Sind alle gedämpften Schwingungen periodisch?
Nein, eine gedämpfte Schwingung ist nur im Schwingfall (kleine Dämpfungskonstante) periodisch. Beim Kriechfall und dem aperiodischen Grenzfall ist die Bewegung nicht periodisch.
Wo treten gedämpfte Schwingungen auf?
Eine gedämpfte Schwingung tritt dort auf, wo Reibungsverluste und Energieumwandlungen vorherrschen. Das ist im allgemeinen immer der Fall. Eine ungedämpfte Schwingung ist also eher eine Modellvorstellung die in der Realität nicht zu realisieren ist.
Welche Fälle können bei einer gedämpften Schwingung auftreten?
Bei einer harmonischen gedämpften Schwingung können drei Fälle eintreten:
Schwingfall
Aperiodischer Grenzfall
Kriechfall
Welche Einheit hat die Dämpfungskonstante?
Die Dämpfungskonstante hat die Einheit \([N\cdot \frac{s}{m}]\)
