Federpendel Schwingungsgleichung
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Das Federpendel
Ein Federpendel besteht aus einer Schraubenfeder an dessen Ende eine Masse befestigt ist, welches sich gradlinig entlang der Auslenkungsrichtung bewegen kann. Während der Bewegung des Pendels verkürzt und verlängert sich die Feder periodisch, die Masse vollführt dabei eine harmonische Bewegung um die Ruhelage. Man nennt ein Federpendel unter anderem auch harmonischer Ozillator oder Federschwinger.
Federpendel Schwingungsgleichung
Für die Herleitung der Schwingungsgleichung ist zunächst der Begriff der Gleichgewichtslage bzw. der Ruhelage wichtig.
Gleichgewichtslage - Ruhelage
Die Gleichgewichtslage bzw. die Ruhelage von einem Federpendel, ist die Position, in der sich das Federpendel befindet, wenn die Gewichtskraft \(F_g\) und die Federkraft \(F_s\) gleich groß sind. Das Federpendel würde ohne äußere Einwirkung in der Ruhelage verbleiben. Es herrscht ein Kräftegleichgewicht zwischen der Gewichtskraft und der Federkraft. Wird das Pendel jedoch nach oben der nach unten ausgelenkt, so ändert sich die Situation.
Auslenkung
Wird das Federpendel wie im unteren Bild aus der Ruhelage nach unten ausgelenkt, so wirkt auf die Masse die Spannkraft \(F_s\) der Feder.
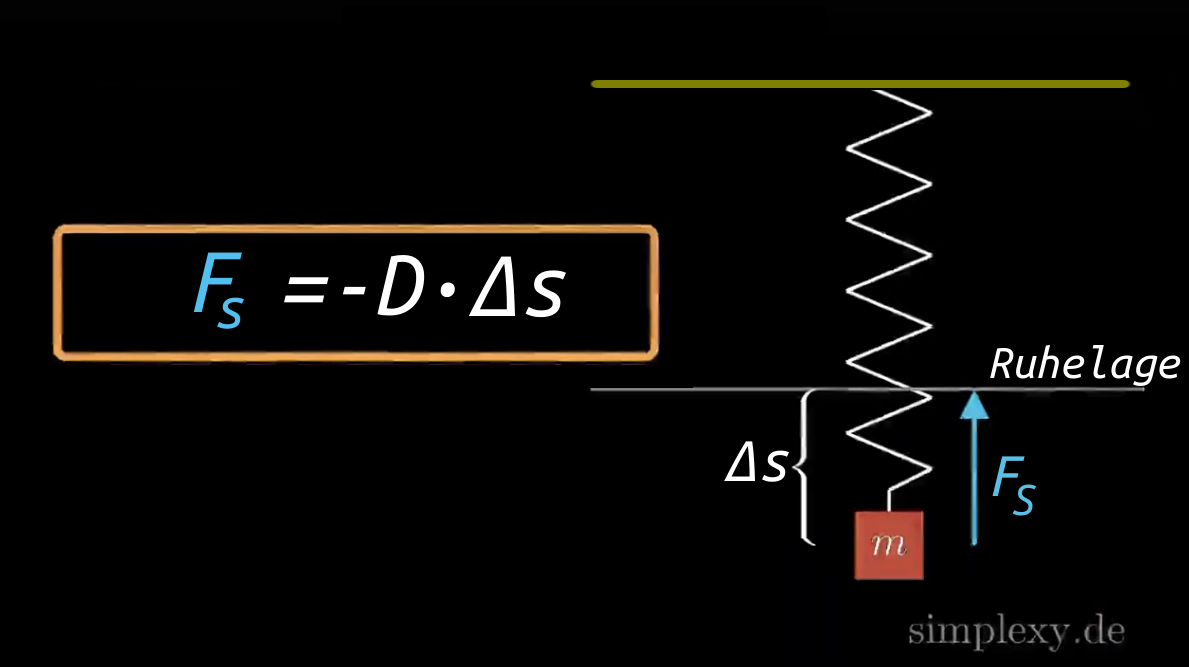
Je größer die Auslenkung aus der Ruhelage ist, desto größer wird die Spannkraft der Feder. Aus dem Hookeschen Gesetzt wissen wir, dass die Spannkraft der Feder wie folgt berechnet werden kann:
\(F_s=-D\cdot \Delta s\)
Dabei ist:
\(D\) die Federkonstante in Newton pro Meter \([\frac{N}{m}]\)
\(\Delta s\) die Auslenkung aus der Ruhelage in Meter \([m]\)
Das Minus-Zeichen gibt an, dass die Federkraft und die Auslenkung entgegengesetzt gerichtet sind.
Info
Die Spannkraft \(F_s\) einer Feder wird auch rücktreibende Kraft genannt.
Oft wird das \(\Delta\) vor dem \(s\) weggelassen um Schreibarbeit zu ersparen, die Gleichung der Federkraft lautet dann:
\(F_s=-D\cdot s\)
Schwingungsgleichung Herleitung
Die Herleitung der Schwingungsgleichung vom Federpendel ist in dem unteren Video leicht erklärt.
Man kann nach dem zweiten Newtonischen Gesetz jede Kraft als Produkt aus Masse und Beschleunigung schrieben \((F=m\cdot a)\), dass gilt auch für die Spannkraft der Feder. Daher kann man schreiben
\(F_s=-D\cdot s=m\cdot a\)
und damit
\(-D\cdot s=m\cdot a\)
Hierbei ist \(a\) die Beschleunigung in vertikaler Richtung, die Beschleunigung kann stets als zweite Ableitung der Strecke (hier die Auslenkung) nach der Zeit \(t\) aufgefasst werden.
\(a=\ddot{s}(t)\)
setzt man dies nun in die letzte Gleichung ein so erhält man:
\(-D\cdot s=m\cdot\ddot{s}(t)\)
Wir können diese Gleichung nun so umstellen das auf der rechten Seite eine Null steht
\(m\cdot\ddot{s}(t)+D\cdot s=0\)
Teilt man nun die Gleichung durch die Masse \(m\), so erhält man die Schwingungsgleichung (Differentialgleichung) vom Federpendel.
Schwingungsgleichung Federpendel
\(\ddot{s}(t)+\)\(\frac{D}{m}\)\(\cdot s=0\)
Wie Löst man die Schwingungsgleichung vom Federpendel?
Zunächst wollen wir uns klar machen was die Differentialgleichung des Federpendels aussagt, dazu stellen wir die Gleichung folgendermaßen dar
\(\ddot{s}(t)=-\)\(\frac{D}{m}\)\(\cdot s\)
Gesucht ist eine Funktion \(s(t)\), die nach zweimaligem Ableiten nach der Zeit wieder auf die Funktion \(s(t)\) und einen konstanten Faktor \(-\frac{D}{m}\) zurückführt. Wir müssen also eine Funktion \(s(t)\) finden deren zweite Ableitung wieder auf die Ursprungsfunktion führt und einen konstanten Faktor
\(\ddot{s}(t)=k\cdot s(t)\)
Eine bereits bekannte Funktion, die diese Bedingung erfüllt, ist die Cosinus-Funktion \(cos(\varphi)\). Unsere Funktion \(s(t)\) muss also proportional zur Cosinus-Funktion sein
\(s\propto cos(\varphi)\)
Da die Auslenkung des Pendels \(s\) in Abhängigkeit von der Zeit \(t\) ist, gilt:
\(\varphi=\omega\cdot t\)
dabei ist \(\omega\) eine Konstante, welche man Kreisfrequenz nennt. Setzen wir dies nun in die Cosinus-Funktion ein so erhalten wir:
\(s(t)=cos(\omega\cdot t)\)
Kreisfrequenz - Eigenfrequenz
\(\omega=\)\(\frac{2\pi}{T}\)
Wie in dem unteren Video erläutert, gibt die Kreisfrequenz an, wie schnell sich ein Punkt um den Einheitskreis bewegen muss, damit er innerhalb einer Schwingungsperiode vom Federpendel genau ein mal um den Kreis gelangt.
Das hier betrachtete Pendel hat zu beginn die größte Auslenkung und wird dann losgelassen, daher ist die Cosinus-Funktion als Lösungsansatz geeignet.
Betrachtet man jedoch ein Pendel das zu Beginn \((t=0)\) in der Ruhelage ist und von dort angestoßen wird, so eignet sich die Sinus-Funktion als Lösungsansatz.
Um zu zeigen das die Cosinus-Funktion unsere Anforderungen erfüllt, leiten wir nun \(s(t)\) zwei mal nach der Zeit ab
\(s(t)=cos(\omega\cdot t)\)
Erste Ableitung: \(\dot{s}(t)=-\omega\cdot sin(\omega\cdot t)\)
Zweite Ableitung: \(\ddot{s}(t)=-\omega^2\cdot cos(\omega\cdot t)\)
Betrachtet man die zweite Ableitung der Funktion \(s(t)\) so sehen wir, dass wir die Ausgangsfunktion \(s(t)=cos(\omega\cdot t)\) und einen zusätzlichen Faktor \(\omega^2\) erhalten. Wir setzten nun \(s(t)\) und die zweite ableitung \(\ddot{s}(t)\) in die Differentialgleichung des Pendels ein und erhalten
\(\ddot{s}(t)+\)\(\frac{D}{m}\)\(\cdot s=0\)
\(-\omega^2\cdot cos(\omega\cdot t)+\)\(\frac{D}{m}\)\(\cdot cos(\omega\cdot t) =0\)
\(-\omega^2\cdot s(t)+\)\(\frac{D}{m}\)\(\cdot s(t) =0\)
Hier kann man als nächsten Schritt das \(s(t)\) ausklammern
\(s(t)(-\omega^2+\)\(\frac{D}{m})\)\(=0\)
Damit diese Gleichung erfüllt ist, muss gelten:
\(-\omega^2+\)\(\frac{D}{m}\)\(=0\)
und damit
\(\omega^2=\)\(\frac{D}{m}\)
Kreisfrequenz - Eigenfrequenz
\(\omega_0=\)\(\sqrt{\frac{D}{m}}\)
Die Eigenfrequenz eines Pendels ist umso größer, je Größer die Federkonstante \(D\) der Feder ist.
Je Größer die Masse \(m\) des Pendels ist, desto kleiner ist die Eigenfrequenz.
Eine Feder mit einer großen Federkonstante nennt man harte Feder, eine Feder mit einer kleinen Federkonstante nennt man weiche Feder.
Periodendauer Federpendel
Aus dem Video wissen wir, dass sich die Kreisfrequenz über
\(\omega_0=\)\(\frac{2\pi}{T}\)
berechnet.
Gleichzeitig wissen wir, dass für die Kreisfrequenz folgende Formel gilt:
\(\omega_0=\)\(\sqrt{\frac{D}{m}}\)
Wir können also beide Formeln gleichsetzen und erhalten:
\(\frac{2\pi}{T}=\sqrt{\frac{D}{m}}\)
Diese Gleichung können wir nun nach \(T\) umstellen und wir erhalten die Periodendauer.
\(T=2\pi\)\(\sqrt{\frac{m}{D}}\)
Periodendauer - Schwingungsdauer Federpendel
\(T=2\pi\)\(\sqrt{\frac{m}{D}}\)
Die Periodendauer bzw. Schwingungsdauer gibt an wie lange das Federpendel für eine vollständige Schwingung bzw. Periode benötigt. Die Periodendauer hat die Einheit Sekunde \([s]\).
Frequenz
Die Frequenz vom Federpendel berechnet sich über den Kehrwert der Schwingungsdauer
Frequenz
\(f=\)\(\frac{1}{T}\)
Die Frequenz gibt an, wie viele vollständige Schwingungen bzw. Perioden innerhalb einer Sekunde stattfinden. Die Frequenz hat die Einheit \([\frac{1}{s}]\).
Wir können die Formel für die Frequenz nach \(T\) umstellen und mit der Formel für die Periodendauer gleichsetzen.
Wir setzen
\(T=\)\(\frac{1}{f}\)
und
\(T=2\pi\)\(\sqrt{\frac{m}{D}}\)
gleich, und erhalten:
\(\frac{1}{f}\)\(=2\pi\)\(\sqrt{\frac{m}{D}}\)
\(\implies f=\)\(\frac{1}{2\pi}\sqrt{\frac{D}{m}}\)
Frequenz Federpendel
\(f=\)\(\frac{1}{2\pi}\sqrt{\frac{D}{m}}\)
Die Frequenz vom Federpendel gibt die Anzahl an Perioden die innerhalb einer Sekunde stattfinden an.
Federpendel Geschwindigkeit
Wir wissen nun wie die Ort-Zeit-Funktion vom Federpendel lautet. Das Federpendel vollführt eine harmonisch Schwingung mit der Ort-Zeit-Funktion
\(s(t)=A\cdot cos(\omega_0 t)\)
Dabei ist \(\omega_0\) die Eigenfrequenz bzw. Kreisfrequenz des Federpendels.
\(\omega_0=\sqrt{\frac{D}{m}}\)
\(A\) ist die Startauslenkung (Amplitude) des Federpendels.
Wie kann man die Geschwindigkeit vom Federpendel berechnen?
Um diese Frage zu beantworten befassen wir uns erst einmal mit der Bewegung des Federpendels sobald man es loslässt.
Wir nehmen an, dass wir das Federpendel nach oben auslenken und dann los lassen. Das Federpendel wird sich in Richtung der Ruhelage beschleunigen. Aufgrund der Trägheit fliegt das Massestück durch die Ruhelage hindurch und gelangt zum unteren Umkehrpunkt. Dort kommt das Pendel für einen kurzen Moment zum Stillstand, und wird anschließend wieder durch die Feder nach oben gezogen.
Während das Pendel durch die Ruhelage fliegt, ist die Geschwindigkeit maximal. Sobald das Federpendel zu den Umkehrpunkten gelangt ist die Geschwindigkeit für einen kleinen Moment Null \((v=0)\).
Die Geschwindigkeit eines Körpers in der Mechanik lässt sich ganz allgemein über die zeitliche Ableitung der Ort-Zeit-Funktion \(\dot{s}(t)\) berechnen. Das gleiche gilt auch für den zeitlichen Verlauf der Geschwindigkeit vom Federpendel.
Geschwindigkeit
\(v=\)\(\frac{\Delta s}{\Delta t}\)
bzw.
\(v=\dot{s}\)
Um den zeitlichen Verlauf der Geschwindigkeit zu ermitteln müssen wir also die Ort-Zeit-Funktion des Pendels einmal nach der Zeit ableiten.
\(\begin{aligned} s(t)&=A\,\,cos(\omega_0 t)\\ \\ \dot{s}(t)&=-A\cdot \omega_0\cdot sin(\omega_0 t) \end{aligned}\)
Hinweis
Bei der Ableitung von \(s(t)\) wurde verwendet:
\(cos(\omega_0 t)'=-\omega_0 sin(\omega_0 t)\)
Die Ableitung vom Cosinus ist der Minus Sinus. Des Weiteren wurde die Kettenregel verwendet.
Geschwindigkeit Federpendel
\(v(t)=-A\cdot \omega_0\cdot sin(\omega_0 t)\)
Wie sieht der zeitliche Verlauf der Geschwindigkeit des Federpendels aus?
Für den Fall das die Amplitude \(A=1\) ist und die Kreisfrequenz \(\omega_0=1\) ist, hat man den folgenden Verlauf für die Ort-Zeit-Funktion \(s(t)\) und der Geschwindigkeit \(v(t)\) des Federpendels:
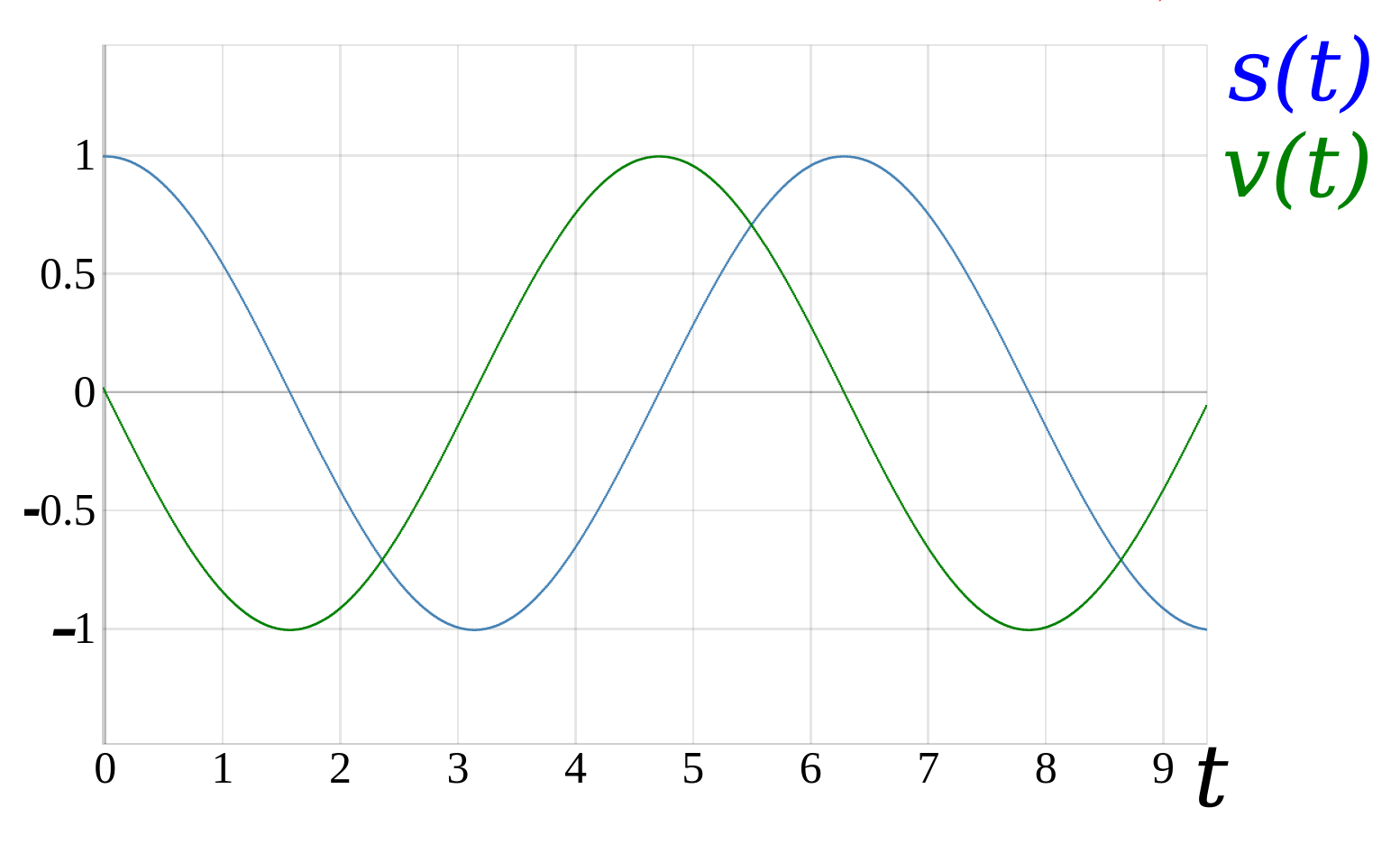
An dem oberen Graph sieht man, dass zum Zeitpunkt \(t=0\) das Federpendel nach oben ausgelenkt ist und die Geschwindigkeit ist null. Sobald das Federpendel los gelassen wird, bewegt es sich in Richtung der Ruhelage (x-Achse) und die Geschwindigkeit nimmt zu. Sobald das Federpendel die Ruhelage erreicht hat, ist die Geschwindigkeit maximal. Das Federpendel bewegt sich anschließend zum unteren Umkehrpunkt und verliert dabei an Geschwindigkeit. Am unteren Umkehrpunkt angekommt ist die Geschwindigkeit auf Null gefallen. Im Anschluss wird die Masse wieder nach oben gezogen und die Geschwindigkeit nimmt zu. Eine negative Auslenkung entspricht einer Position des Federpendels unterhalb der Ruhelage. Eine negative Geschwindigkeit entspricht einer Bewegungsrichtung nach unten.
Merke
Die hier betrachtete Ort-Zeit-Funktion \(s(t)=A\cdot cos(\omega\cdot t)\), geht einher mit einem Federpendel das zum start Zeitpunkt \(t=0\) nach oben ausgelenkt ist. Man kann ein Federpendel zum start Zeitpunkt in der Ruhelage lassen und dann anstoßen. Die Ort-Zeit-Funktion wäre dann:
\(s(t)=A\cdot sin(\omega\cdot t)\)
und damit wäre die Geschwindigkeit für diesen Fall:
\(v(t)=A\cdot \omega\cdot cos(\omega t)\)
Die Ort-Zeit-Funktion und damit auch der zeitliche Verlauf der Geschwindigkeit ist von der Anfangsbedingung abhängig.
Federpendel Beschleunigung
Mit der gleichen Vorgehensweise können wir die Beschleunigung des Federpendels ermitteln.
Um den zeitlichen Verlauf der Beschleunigung vom Federpendel zu erhalten, können wir die Ort-Zeit-Funktion \(s(t)\) zwei mal nach der Zeit ableiten bzw. die Geschwindigkeit \(v(t)\) einmal nach der Zeit ableiten
Beschleunigung
\(a=\)\(\frac{\Delta v}{\Delta t}\)
bzw.
\(a=\dot{v}=\ddot{s}\)
Wir müssen also nun die Ort-Zeit-Funktion \(s(t)\) zwei mal nach der Zeit ableiten oder die Geschwindigkeit \(v(t)\) einmal nach der Zeit ableiten um auf die Beschleunigung vom Pendel zu kommen.
Beschleunigung des Federpendels
\(a(t)=\dot{v}(t)\)
\(a(t)=-A\cdot \omega^2\cdot cos(\omega\cdot t)\)
Wir haben auch hier die Kettenregel verwendet um die Ableitung zu berechnen.
Die äußeren Ableitung von \(-sin(\omega t)\) lautet:
\(-cos(\omega\cdot t)\)
und die innere Ableitung lautet:
\(\frac{d(\omega\cdot t)}{dt}\)\(=\omega\)
Die innere Ableitung mal die äußere Ableitung liefert also:
\(a(t)=-A\cdot \omega^2\cdot cos(\omega t)\)
Der zeitliche Verlauf von \(s(t)\), \(v(t)\) und \(a(t)\) sieht wie folgt aus:
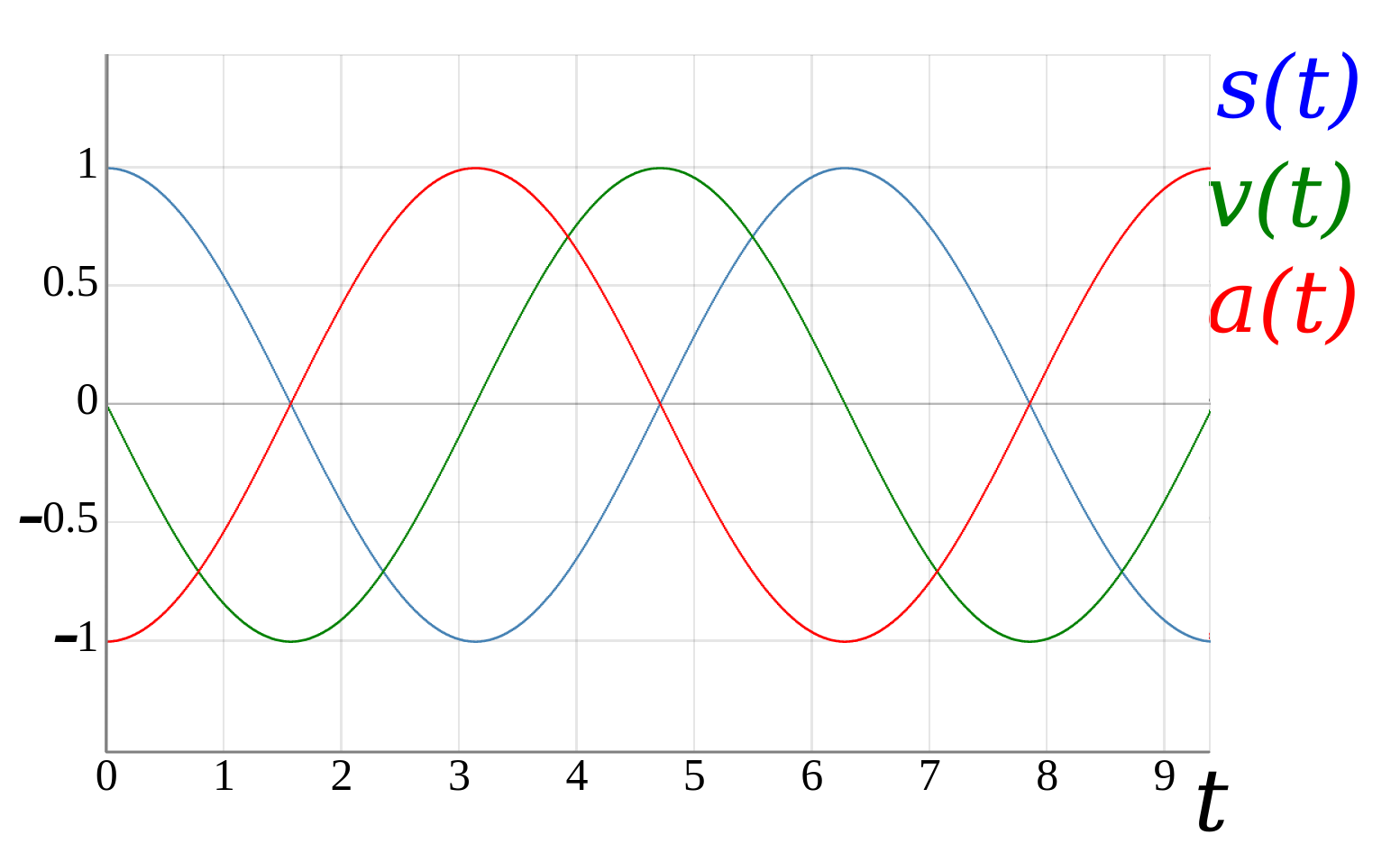
Wie man in der oberen Abbildung sieht, ist die Geschwindigkeit zum start Zeitpunkt Null und die Auslenkung des Pendels ist maximal. Während sich das Pendel in Richtung der Ruhelage bewegt, steigt die Geschwindigkeit des Pendel, beim Durchgang durch die Ruhelage (Nullpunkt) ist die Geschwindigkeit des Pendels maximal und die Auslenkung des Pendels Null.
Die Beschleunigung des Pendels ist an den Umkehrpunkten maximal da sich die Bewegungsrichtung des Pendels umkehren muss. Das Pendel wird abgebremmst und in die entgegengesetzte Richtung beschleunigt. Beim Durchgang durch die Ruhelage ist die Beschleunigung Null, da die Geschwindigkeit dort maximal ist und sich für einen kurzen moment nicht ändert.
Zusammenfassung ungedämpftes Federpendel
Die Schwingungsgleichung eines Federpendels kann man aus dem Hookeschen Gesetzt ableiten.
Die Schwingungsgleichung lautet:
\(m\cdot \ddot{s}(t)+D\cdot s(t)=0\)
Dabei ist:
\(m\) die Masse,
\(s(t)\) die Auslenkung,
und \(D\) die Federkonstante des Pendels.
Das Federpendel schwingt harmonisch mit der Ort-Zeit-Funktion
\(s(t)=A\cdot cos(\omega_0 t)\)
Dabei ist \(\omega_0\) die Eigenfrequenz bzw. Kreisfrequenz des Pendels.
\(A\) ist die Startauslenkung des Pendels.
\(\omega_0=\sqrt{\frac{D}{m}}\)
Die Schwingungsdauer bzw. die Periodendauer berechnet sich über
Die Frequenz berechnet sich über
\(T=\)\(\frac{2\pi}{\omega_0}\)
\(T=2\pi\cdot\sqrt{\frac{m}{D}}\)
\(f=\frac{1}{T}\)
Federpendel gedämpft
Die gedämpfte Schwingung vom Federpendel kann auch als gedämpfte harmonische Schwingung oder freie gedämpfte Schwingung genannt werden.
Die Dämpfung beim Federpendel macht sich bemerkbar über eine zeitliche Abnahme der Amplitude. Eine Dämpfung kommt zustande, durch eine Wechselwirkung des Pendels mit dem Medium in dem es Schwingt. Findet die Schwingung in Luft statt, so herrscht ein Luftwiderstand. Das Pendel muss die Luft verdrängen in dem es Schwingt, dies sorgt für Reibungsverluste und das Federpendel wird abgebremst. Mathematisch wird die Dämpfung über eine Dämpfungskonstante und eine Abklingkonstante beschrieben.
Bewegungsgleichung gedämpftes Federpendel
Um die Bewegungsgleichung für das gedämpfte Federpendel zu erhalten, muss man den Einfluss der Luftreibung berücksichtigen. Zusätzlich zu der Beschleunigungskraft und der Spannkraft der Feder
\(m\cdot \ddot{s}(t)=-D\cdot s(t)\)
muss die Kraft welche durch die Luftreibung zu stande kommt berücksichtigt werden. Dabei ist die Luftreibung proportional zu der Geschwindigkeit \(v(t)\) des Pendels. Die Formel für die Kraft durch die Luftreibung lautet wie folgt.
Luftreibung
\(F_{LR}=k\cdot v(t)\)
Dabei ist \(k\) die Reibungskonstante mit der Einheit \([N\cdot \frac{s}{m}]\).
Die Reibungskonstante ist abhängig von der Wechselwirkung zwischen dem Pendel und der Luft. Je aerodynamischer die Pendelmasse ist, desto kleiner ist die Reibungskonstante. Das Medium in dem das Pendel schwingt beeinflusst die Reibungskonstante ebenso. Schwingt das Pendel ist einer Flüssigkeit, so lässt sich die Flüssigkeit schwerer verdrängen und die Reibungskonstante wäre dementsprechend größer.
Der Einfluss der Luftreibung lässt sich in die Bewegungsgleichung des Federpendels wie folgt einbringen:
\(m\cdot \ddot{s}(t)=-D\cdot s(t)-\underbrace{k\cdot v(t)}_{F_{LR}}\)
Das Minus vor dem Term für die Luftreibung \(F_{LR}\) kommt daher, dass die Luftreibung in die entgegengesetzte Richtung wie die Bewegungsrichtung wirkt. Bewegt sich das Pendel nach unten, so herrscht ein Luftwiderstand nach oben. Bewegt sich das Pendel nach oben, so drückt der Luftwiderstand nach unten.
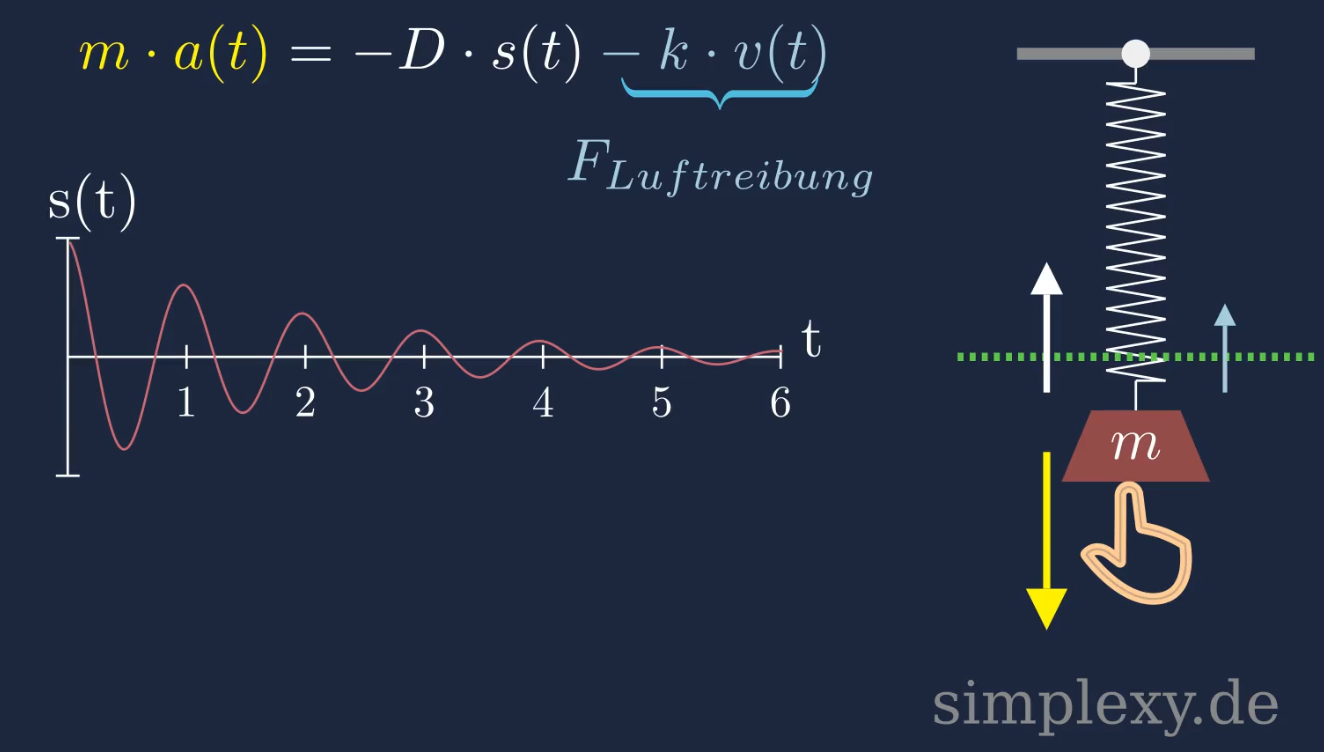
Man kann \(v(t)\) mit \(\dot{s}(t)\) ersetzen so dass man folgende Bewegungsgleichung hat:
\(m\cdot \ddot{s}(t)=-D\cdot s(t)-k\cdot \dot{s}(t)\)
Diese Bewegungsgleichung kann man nun noch etwas umformen so das man zu der üblichen Form der gedämpften Bewegungsgleichung des Federpendels kommt.
Bewegungsgleichung gedämpftes Federpendel
\(\ddot{s}(t)+\frac{D}{m}\cdot s(t)+\frac{k}{m}\cdot \dot{s}(t)=0\)
Wie löst man die Bewegungsgleichung des gedämpften Federpendels?
Um die Bewegungsgleichung des gedämpften Federpendels zu lösen nutzen wir einen "Exponential-Ansatz".
\(\begin{aligned} s(t)&=c\cdot e^{\lambda t}\\ \dot{s}(t)&=c\cdot\lambda\,\,e^{\lambda t}\\ \ddot{s}(t)&=c\cdot\lambda^2\,\,e^{\lambda t} \end{aligned}\)
Wird der Ansatz in die Bewegungsgleichung eingesetzt, so erhlaten wir:
\( \lambda^2\,c\,e^{\lambda t}+\frac{D}{m}\,c\,e^{\lambda t}+\frac{k}{m}\,\lambda\,c\,e^{\lambda t}=0 \)
Nun können wir den Term \(ce^{\lambda t}\) kürzen:
\( \lambda^2\,\bcancel{c\,e^{\lambda t}}+\frac{D}{m}\, \bcancel{c\,e^{\lambda t}}+\frac{k}{m}\,\lambda\,\bcancel{c\, e^{\lambda t}}=0 \)
Übrig bleibt die folgende quadratische Gleichung welche mit der pq-Formel gelöst werden kann.
\( \lambda^2+\frac{k}{m}\,\lambda+\frac{D}{m}=0 \)
\(\implies\)
\( \lambda_{1,2}=-\frac{k}{2m}\pm\sqrt{\big(\frac{k}{2m}\big)^2-\frac{D}{m}} \)
Für eine bessere Darstellung von \(\lambda_{1,2}\), nehmen wir die folgenden Definitionen vor:
\(\begin{aligned} \omega_0&=\sqrt{\frac{D}{m}}\\ \\ \delta&=\frac{k}{2m} \end{aligned}\)
\(\implies\)
\( \lambda_{1,2}=-\delta\pm\sqrt{\delta^2-\omega_0^2} \)
Dabei ist \(\omega_0\) die Eigenfrequenz des ungedämpften Federpendels und \(\delta\) wird als Abklingkonstante bezeichnet. Damit haben wir nun zwei linear unabhängige Lösungen \(s_1(t)\) und \(s_2(t)\)
\(\begin{aligned} s_1(t)&=c_1\cdot e^{\lambda_1 t}\\ \\ s_2(t)&=c_2\cdot e^{\lambda_2 t}\\ \end{aligned}\)
Das weitere Vorgehen hängt von drei Fallunterscheidungen bzgl. der Diskriminante in \(\lambda_{1,2}\) ab. Je nachdem wie \(\omega_0\) und \(\delta\) gewählt werden, hat man den Schwingfall, Kriechfall oder den aperiodischen Grenzfall.
Schwingfall
Ist die Dämpfungskonstante \(k\) bzw. die Abklingkonstante \(\delta\) kleiner als die Eigenfrequenz \(\omega_0\)
\(\delta^2\lt\omega_0^2\)
so wird die Diskriminante \(\delta^2-\omega_0^2\) aus \(\lambda_{1,2}\) negativ. Der Wurzelausdruck wird damit komplex.
\( \lambda_{1,2}=-\delta\pm\underbrace{\sqrt{\delta^2-\omega_0^2}}_{imaginär} \)
Für eine besser Übersicht definieren wir
\( \omega^2=\omega_0^2-\delta^2 \)
\(\implies\)
\(\begin{aligned} \lambda_{1,2}&=-\delta\pm\sqrt{-\omega^2}\\ \\ &=-\delta\pm\omega\underbrace{\sqrt{-1}}_{i}\\ \\ &=-\delta\pm i\,\omega \end{aligned}\)
Setzt man nun \(\lambda_{1}\) in \(s_1(t)\) ein und \(\lambda_{2}\) in \(s_2(t)\) ein so erhält man:
\(\begin{aligned} s_1(t)&=c_1\cdot e^{(-\delta+i\omega)t}\\ \\ s_2(t)&=c_2\cdot e^{(-\delta-i\omega)t} \end{aligned}\)
Jede beliebige Lösung \(s(t)\) kann als linear kombination von \(s_1(t)\) und \(s_2(t)\) geschrieben werden.
\(\begin{aligned} s(t)&=c_1 e^{(-\delta+i\omega)t}+c_2 e^{(-\delta-i\omega)t}\\ \\ &=e^{-\delta t}\big(\underbrace{c_1e^{i\omega t}+c_2e^{-i\omega t}}_{A\,cos(\omega\,t+\varphi)}\big)\\ \\ &=A\,e^{-\delta t}\,cos(\omega\,t+\varphi) \end{aligned}\)
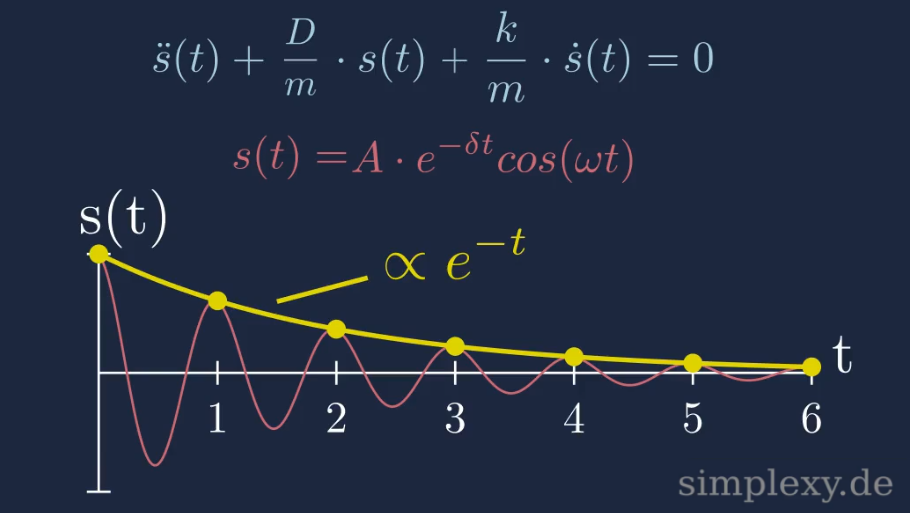
Kriechfall
Der Kriechfall entsteht wenn die Dämpfungskonstante \(k\) bzw. Abklingkonstante \(\delta\) größer als die Eigenfrequenz des Pendels ist.
\(\delta^2\gt\omega^2\)
Im Kriechfall ist die Diskriminante von \(\lambda_{1,2}\) positiv. Die Lösungen \(s_1(t)\) und \(s_2(t)\) sind damit reell.
\( \lambda_{1,2}=-\delta\pm\underbrace{\sqrt{\delta^2-\omega^2}}_{\alpha} \)
\(\implies\)
\(\begin{aligned} s_1(t)&=c_1\cdot e^{(-\delta+\alpha)t}\\ \\ s_2(t)&=c_2\cdot e^{(-\delta-\alpha)t} \end{aligned}\)
Eine beliebige Lösung \(s(t)\) kann als linear kombination von \(s_1(t)\) und \(s_2(t)\) ausgedrückt werden.
\(\begin{aligned} s(t)&=c_1 e^{(-\delta+\alpha)t}+c_2 e^{(-\delta-\alpha)t}\\ \\ &=e^{-\delta t}\big(c_1e^{\alpha t}+c_2e^{-\alpha t}\big)\\ \end{aligned}\)
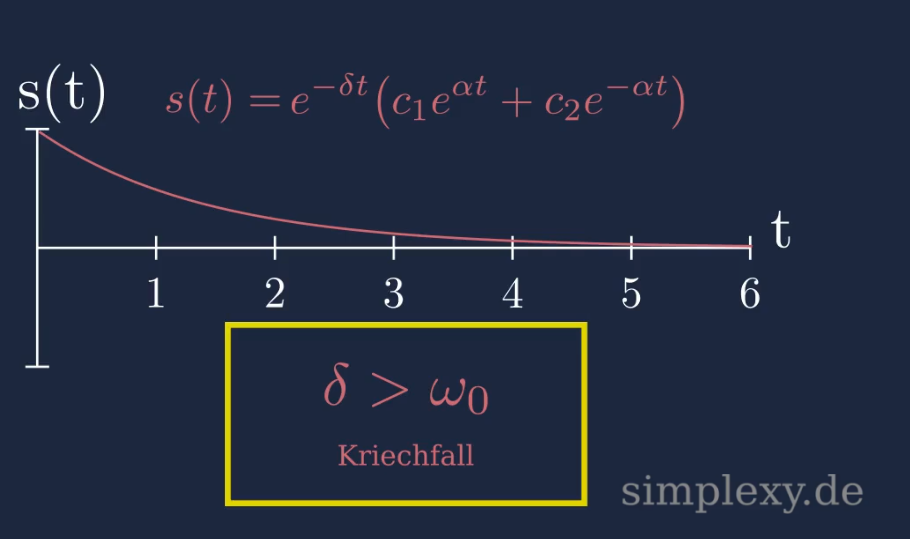
Beim Kriechfall ist keine Schwingung vorhanden. Das Federpendel bewegt sich langsam in Richtung der Ruhelage und verbleibt dort. Dies ist auf die hohe Dämpfungskonstante zurück zu führen. Solch ein Verhalten ist zu beobachten wenn ein Federpendel in einer Flüssigkeit mit niederiger Viskosität (Öl, Honig, etc.) ausglenkt und los gelassen wird.
Aperiodischer Grenzfall
Beim aperiodischen Grenzfall ist die Abklingkonstante \(\delta\) so groß wie die Eigenfrequenz \(\omega_0\)
\(\delta^2=\omega_0^2\)
\( \lambda_{1,2}=-\delta\pm\underbrace{\sqrt{\delta^2-\omega^2}}_{=0} \)
\(\implies\)
\(\begin{aligned} s_1(t)&=c_1\cdot e^{-\delta t}\\ \\ s_2(t)&=c_2\cdot e^{-\delta t} \end{aligned}\)
Damit sind \(s_1(t)\) und \(s_2(t)\) nicht linear unabhängig. Da die Differentialgleichung vom gedämpften Federpendel eine dgl zweiter Ordnung ist, müssen zwei linear unabhängige Lösung vorhanden sein. Um \(s_1(t)\) und \(s_2(t)\) linear unabhängig zu machen, kann man bei einem der zwei ein \(t\) hinzu multiplizieren. Wir machen dies bei \(s_2(t)\)
\(\begin{aligned} s_1(t)&=c_1\cdot e^{-\delta t}\\ \\ s_2(t)&=c_2\cdot t\,\cdot e^{-\delta t} \end{aligned}\)
Trotz der multiplikation mit \(t\) bei \(s_2(t)\), ist das eine Lösung der Differentialgleichung für den Fall, dass \(\omega_0=\delta\). Als Probe kann man \(s_2(t)\) in die dgl einsetzten, man stellt fest, dass es sich dabei um eine valide Lösung handelt. Damit kann nun eine beliebige Lösung \(s(t)\) als linear kombination von \(s_1(t)\) und \(s_2(t)\) geschrieben werden.
\(\begin{aligned} s(t)&=c_1 e^{-\delta t}+c_2\cdot t\, e^{-\delta t}\\ \\ &=e^{-\delta t}\big(c_1+c_2\cdot t\big)\\ \end{aligned}\)

Beim aperiodischen Grenzfall ist die kleinstmögliche Dämpfungskonstante vorhanden, die zu einer Lösung ohne Schwingung führt. Ähnlich wie beim Kriechfall bewegt sich das Federpendel zur Ruhelage ohne eine Schwingung zu vollführen.
