Kreisbewegung
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Die Kreisbewegung
Bewegt sich ein Körper auf einer Kreisbahn mit festem Radius, so nennt man diese Bewegung eine Kreisbewegung. Ist die Geschwindigkeit des Körpers konstant, so bezeichnet man die Bewegung als gleichförmige Kreisbewegung. Damit sich ein Körper auf einer Kreisbahn bewegt, muss er dazu "gezwungen" werden. Der Körper muss in Richtung des Mittelpunktes (Drehachse) beschleunigt werden. Es herrscht eine permanente Änderung der Bewegungsrichtung.
Jede Kreisbewegung ist eine beschleunigte Bewegung, selbst wenn die Bahngeschwindigkeit konstant ist.
Was ist eine Kreisbewegung?
Eine Kreisbewegung zeichnet sich dadurch aus, dass sich die Bewegungsrichtung ständig ändert. Nur so kann ein Körper entlang einer Kreisbahn bewegt werden. Mit der Änderung der Bewegungsrichtung geht auch eine Änderung der Geschwindigkeitsrichtung einher. Die Geschwindigkeit eines Körpers, der sich auf einer Kreisbahn bewegt, wird Bahngeschwindigkeit genannt. Ist die Bahngeschwindigkeit konstant, so nennt man die Kreisbewegung, eine gleichförmige Kreisbewegung.
Gleichförmige Kreisbewegung
Eine gleichförmige Kreisbewegung ist eine Kreisbewegung, mit einer betragsmäßig konstanten Bahngeschwindigkeit. Eine Änderung der Bewegungsrichtung findet trotzallem statt.
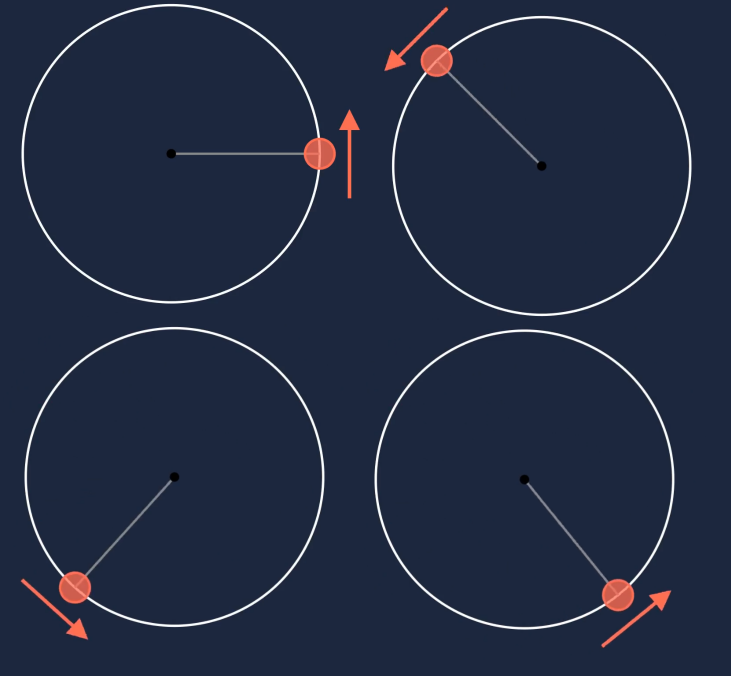
In der oberen Abbildung kann man sehen, wie sich die Bewegungsrichtung des roten Punktes ändern muss, um auf der Kreisbahn zu bleiben. Mit der Änderung der Bewegungsrichtung, findet auch eine Änderung der Geschwindigkeitsrichtung statt. Die Geschwindigkeit des Punkts ist tangential zur Kreisbahn gerichtet. In der unteren Abbildung ist der Geschwindigkeitsvektor \(\vec{v}\) dargestellt.
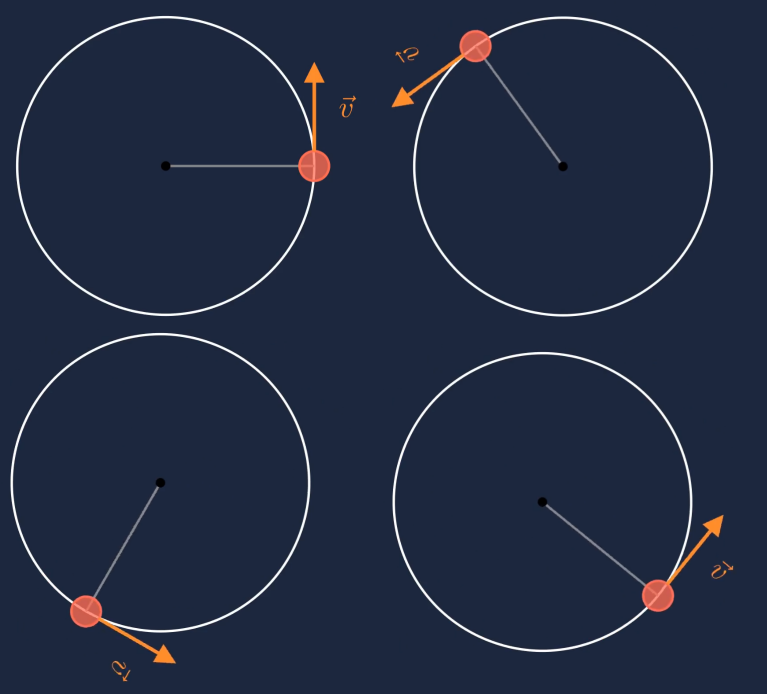
Der Geschwindigkeitsvektor ist tangential zur Kreisbahn orientiert. Sein Betrag (Länge) ist zu jedem Zeitpunkt gleich (konstant). Es handelt sich also um eine gleichförmige Kreisbewegung.
Größen der Kreisbewegung
Um eine Kreisbewegung mathematisch beschreiben zu können, werden die folgenden Größen benötigt:
-
Radius \(r\,\text{in }[m]\): Entfernung des Körpers vom Mittelpunkt (Drehachse) der Kreisbahn.
-
Umlaufdauer \(T\,\text{in }[s]\): Die Zeit, welche vom Körper benötigt wird, um einen Umlauf um die Kreisbahn zu verrichten.
-
Frequenz \(f\,\text{in }[\frac{1}{s}]\): Die Frequenz gibt an, wie viele Umläufe innerhalb einer Sekunde statt finden.
-
Bahngeschwindigkeit \(v\,\text{in }[\frac{m}{s}]\): Die Geschwindigkeit des Körpers auf seiner Kreisbahn.
-
Winkelgeschwindigkeit \(\omega\,\text{in }[\frac{rad}{s}]\): Die Winkelgeschwindigkeit gibt an, wie schnell sich ein Winkel mit der Zeit um eine Achse ändert.
Umlaufdauer / Periodendauer
Die Umlaufdauer \(T\) gibt die Zeit an, die ein Körper für eine volle Umrundung benötigt. Die Einheit der Umlaufdauer ist Sekunden \([s]\). Oftmals wird die Umlaufdauer auch als Periodendauer bezeichnet.
Frequenz
Die Frequenz \(f\) gibt an, wie viele Umläufe pro Sekunde statt finden. Die Frequenz steht in Zusammenhang mit der Umlaufdauer.
Frequenz
Die Frequenz gibt an, wie viele Umläufe \(N\) ein Körper innerhalb einer Sekunde verrichtet.
\(\begin{aligned} f=\frac{N}{s} \end{aligned}\)
Die Einheit der Frequenz ist \(Hz\) (Hertz) bzw \(\frac{1}{s}\).
Die Frequenz und die Umlaufdauer stehen in Zusammenhang mit einander:
\(\begin{aligned} f&=\frac{1}{T}\\ \\ T&=\frac{1}{f} \end{aligned}\)
Bahngeschwindigkeit
Die Bahngeschwindigkeit eines Körpers während einer Kreisbewegung kann so berechnet werden, wie man es aus der Mechanik kennt.
\(\begin{aligned} v=\frac{\Delta s}{\Delta t} \end{aligned}\)
Wobei \(\Delta s\) für einen Streckenabschnitt steht und \(\Delta t\) für den Zeitabschnitt, welcher vom Körper benötigt wird um den Streckabschnitt \(\Delta s\) zurück zu legen.
Für die Herleitung der Formel für die Bahngeschwindigkeit, nutzen wir als Streckabschnitt \(\Delta s\), eine volle Umrundung. Bewegt sich der Körper auf einer Kreisbahn mit dem Radius \(r\), so ist der Umfang \(U\) der Kreisbahn genauso groß wie die Strecke welche innerhalb einer Umrundung zurück gelegt wird.
\(\begin{aligned} U = 2\pi r \end{aligned}\)
\(\begin{aligned} \Delta s &=U\\ \\ \Delta s &=2\pi r \end{aligned}\)
Um die Formel für die Bahngeschwindigkeit berechnen zu können, benötigt man zusätzlich zum Streckabschnitt \(\Delta s\) noch den Zeitabschnitt \(\Delta t\) welcher benötigt wird, um \(\Delta s\) zurück zu legen. Da wir als \(\Delta s\) eine voll Umrundung betrachten, ist \(\Delta t=T\). Denn innerhalb einer Umlaufdauer \(T\) wird eine volle Umrundung zurück gelegt.
Für die Bahngeschwindigkeit folgt somit:
\(\begin{aligned} v=\frac{2\pi r}{T} \end{aligned}\)
Wie man sieht, ist die Bahngeschwindigkeit abhängig vom Radius \(r\) der Kreisbahn.
Die Bahngeschwindigkeit kann auch über die Frequenz \(f\) ausgedrückt werden. Dazu verwendet man:
\(\begin{aligned} T&=\frac{1}{f} \end{aligned}\)
Für die Bahngeschwindigkeit folgt somit:
\(\begin{aligned} v&=\frac{2\pi r}{T}\\ \\ v&=2\pi rf \end{aligned}\)
Bahngeschwindigkeit Formel
Bahngeschwindigkeit in Abhängigkeit von der Umlaufdauer:
\(\begin{aligned} v=\frac{2\pi r}{T} \end{aligned}\)
Bahngeschwindigkeit in Abhängigkeit von der Frequenz:
\(\begin{aligned} v=2\pi rf \end{aligned}\)
Merke
Die Bahngeschwindigkeit ist vom Radius \(r\) der Kreisbahn abhängig.
Winkelgeschwindigkeit
Eine Kreisbewegung kann auch mit Hilfe der Winkelgeschwindigkeit \(\omega\) beschrieben werden. Die Winkelgeschwindigkeit gibt an, welchen Winkel \(\varphi\) in einem bestimmten Zeitintervall \(\Delta t\) überstrichen wird.
\(\begin{aligned} \omega=\frac{\Delta \varphi}{\Delta t} \end{aligned}\)
Die Einheit der Winkelgeschwindigkeit wird in Bogenmaß angegeben. Statt die Angabe "Grad pro Sekunde", wird die Winkelgeschwindigkeit in \(\frac{rad}{s}\) (Radiant pro Sekunde) angegeben. Im Bogenmaß entpricht ein voller Umlauf (\(360^{\circ}\)) einen Winkel \(\varphi=2\pi\).

Um die Winkelgeschwindigkeit berechnen zu können, nutzen wir aus, dass innerhalb einer Umlaufdauer \(T\) ein Winkel von \(2\pi\) überstrichen wird. Die Winkelgeschwindigkeit lautet somit:
\(\begin{aligned} \omega=\frac{2\pi}{T}=2\pi f \end{aligned}\)
Winkelgeschwindigkeit Formel
Winkelgeschwindigkeit in Abhängigkeit von der Umlaufdauer:
\(\begin{aligned} \omega=\frac{2\pi}{T} \end{aligned}\)
Winkelgeschwindigkeit in Abhängigkeit von der Frequenz:
\(\begin{aligned} \omega=2\pi f \end{aligned}\)
Bahngeschwindigkeit und Winkelgeschwindigkeit - Abhängigkeit
Die Bahngeschwindigkeit \(v\) kann über die Winkelgeschwindigkeit berechnet werden. Dazu muss jedoch der Radius \(r\) der Kreisbahn bekannt sein.
\(\begin{aligned} v=\omega\cdot r \end{aligned}\)
Zwei Körper mit gleicher Winkelgeschwindigkeit können verschiedene Bahngeschwindigkeiten besitzen, wenn ihre Radien unterschiedlich sind.
Bahngeschwindigkeit und Winkelgeschwindigkeit
\(\begin{aligned} v=\omega\cdot r \end{aligned}\)
Kreisbewegung alle Formeln
-
Umlaufdauer
\(\begin{aligned} T=\frac{1}{f} \end{aligned}\)
-
Frequenz
\(\begin{aligned} f=\frac{1}{T} \end{aligned}\)
-
Bahngeschwindigkeit
\(\begin{aligned} v&=\frac{2\pi r}{T}\\ \\ v&=2\pi r f\\ \\ v&=\omega r \end{aligned}\)
-
Winkelgeschwindigkeit
\(\begin{aligned} \omega&=\frac{2\pi}{T}\\ \\ \omega&=2\pi f\\ \\ \omega&=\frac{v}{r} \end{aligned}\)
-
Bahnbeschleunigung
\(\begin{aligned} a&=\frac{v^2}{r} \end{aligned}\)
Beispiel Kreisbewegung berechnen
Beispiel 1
Ein Riesenrad fährt \(2\) Runden in einer Zeit von \(5\,min\). Wie groß ist die Frequenz?
Um die Frequenz zu berechnen, müssen wir die Anzahl der Runden durch die dafür benötigte Zeit teilen.
\(\begin{aligned} f=\frac{2}{5min}=0,4\frac{1}{min} \end{aligned}\)
Die Frequenz wird stetz in \(\frac{1}{s}\) bzw. in Hertz angegeben.
\(\begin{aligned} 0,4\frac{1}{min}=0,4\frac{1}{60}\frac{1}{s}=0,0066Hz \end{aligned}\)
Die Passagiere des Riesenrads sitzen in einem Abstand von \(15m\) zur Drehachse. Mit welcher Bahngeschwindigkeit bewegen sich die Fahrgäste?
Da wir die Frequenz bereits berechnet haben, benötigen wie für die berechnung der Bahngeschwindigkeit noch den Radius. Dieser ist jedoch als Abstand zwischen den Fahrgästen und der Drehachse angegeben (\(r=15m\)). Damit kann die Bahngeschwindigkeit über die folgende Formel berechnet werden:
\(\begin{aligned} v&=2\pi r f\\ \\ v&=2\pi\cdot 15m\cdot 0,006Hz\\ \\ v&=0,565\frac{m}{s} \end{aligned}\)
Beispiel 2
Ein Riesenrad benötigt für eine Umdrehung \(5\) Minuten.
Berechne die Winkelgeschwindigkeit des Riesenrads.
Zunächst müssen wir die Umlaufdauer vom Riesenrad in Sekunden umrechnen.
\(\begin{aligned} T=5\,min=5\cdot\,60\,s=300\,s \end{aligned}\)
Nun verwenden wir die folgende Formel um die Winkelgeschwindigkeit berechnen zu können:
\(\begin{aligned} \omega=\frac{2\pi}{T} \end{aligned}\)
Damit folgt für die Winkelgeschwindigkeit:
\(\begin{aligned} \omega=\frac{2\pi}{300s}=0,021\frac{1}{s} \end{aligned}\)
Beispiel 3
Ein Hamster läuft in seinem Rad und führt dazu, dass die Winkelgeschwindigkeit des Rades \(12,5\frac{1}{s}\) ist. Wie lange dauert eine Umrundung vom Hamsterrad?
Gesucht ist die Umlaufdauer des Hamsterrads. Dazu stellen wir die folgende Formel nach der Umlaufdauer \(T\) um.
\(\begin{aligned} \omega&=\frac{2\pi}{T}\\ \\ &\implies\\ \\ T&=\frac{2\pi}{\omega} \end{aligned}\)
Nun können wir die Umlaufdauer berechnen, indem wir die bekannte Winkelgeschwindigkeit einsetzten.
\(\begin{aligned} T=\frac{2\pi}{12,5\frac{1}{s}}=0,5s \end{aligned}\)
Das Hamsterrad benötigt eine halbe Sekunde für eine Umrundung.
